MeshRegion[{p1,p2,…},{mcell1[{i1,…}],mcell2[{j1,…}],…}]
yields a mesh with cells mcellj, where coordinates given as integer i are taken to be pi.
MeshRegion[…,{…,wi[mcelli[…]],…}]
yields a mesh with cell properties defined by the symbolic wrapper wi.
MeshRegion[mreg,opts]
yields a mesh from a mesh region mreg with options opts.




MeshRegion
MeshRegion[{p1,p2,…},{mcell1[{i1,…}],mcell2[{j1,…}],…}]
yields a mesh with cells mcellj, where coordinates given as integer i are taken to be pi.
MeshRegion[…,{…,wi[mcelli[…]],…}]
yields a mesh with cell properties defined by the symbolic wrapper wi.
MeshRegion[mreg,opts]
yields a mesh from a mesh region mreg with options opts.
Details and Options






- MeshRegion is also known as a simplicial complex or cell complex.
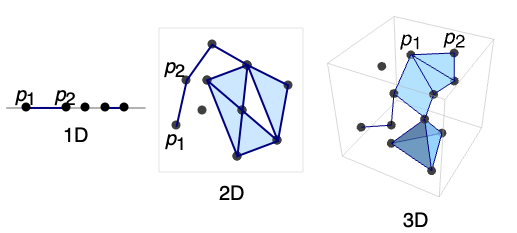
- MeshRegion can represent a piecewise linear region of any geometric dimension embedded in dimension 1, 2, or 3.
- MeshRegion[…] displays in a notebook as a plot of a mesh region.
- MeshRegion is typically created using functions such as DelaunayMesh, DiscretizeGraphics, and DiscretizeRegion.
- The region represented by MeshRegion consists of the disjoint union of mesh cells.
- MeshRegion has an embedding dimension that is equal to the length of each point pi and can be found using RegionEmbeddingDimension.
- Each cell has a geometric dimension and can be found using RegionDimension.
- Possible mesh cells mcelli and their geometric dimensions:
-
Point[i] 0 point Line[{i1,i2,…}] 1 line segments {i1,i2}, {i2,i3}, … Triangle[{i1,i2,i3}] 2 filled triangle Polygon[{i1,i2,…}] 2 filled polygon Polyhedron[{{ii,i2,…},…}] 3 filled polyhedron Tetrahedron[{i1,…,i4}] 3 filled tetrahedron Hexahedron[{i1,…,i8}] 3 filled hexahedron Pyramid[{i1,…,i5}] 3 filled pyramid Prism[{i1,…,i6}] 3 filled prism Simplex[{i1,…,ik}] 0, 1, 2, 3 filled simplex - Tetrahedron, Hexahedron, Pyramid, and Prism can only be used with 3D coordinates.
- Point, Line, Triangle, Polygon, Polyhedron, Tetrahedron, Hexahedron, Pyramid, Prism, and Simplex all have multi-cell specifications as well.
- The following special wrappers wi can be used for cells:
-
Labeled[cell,…] display the cell with labeling Style[cell,…] show the cell with the specified style Annotation[cell,namevalue] associate the annotation name->value with cell - Each cell in a MeshRegion is given a unique MeshCellIndex of the form {d,i}, where d is the geometric dimension and i is the index.
- For purposes of selecting cells of a MeshRegion, the following cell specifications may be used:
-
{d,i} cell with index i of dimension d {d,ispec} cells with index specification ispec of dimension d {dspec,…} cells of dimensions given by dspec h[{i1,…}] explicit cell with head h and vertex indices i1, … {c1,c2,…} list of explicit cells ci - The index specification ispec can have the following form:
-
i cell index i {i1,i2,…} cells with indices ik All all cells patt cells with indices matching the pattern patt - The dimension specification dspec can have the following form:
-
d explicit dimension d All all dimensions from 0 to geometric dimension of region patt dimensions matching the pattern patt - MeshRegion is always converted to an optimized representation and treated as raw by functions like AtomQ and for purposes of pattern matching.
- MeshRegion has the same options as Graphics for embedding dimension 2 and the same options as Graphics3D for embedding dimension 3 with the following additions and changes:
-
MeshCellLabel Automatic labels and placement for cells MeshCellShapeFunction Automatic shape functions for cells MeshCellStyle Automatic styles for cells MeshCellHighlight {} list of highlighted cells MeshCellMarker 0 integer markers for cells PlotTheme $PlotTheme overall theme for the mesh - Possible settings for PlotTheme include common base themes, font features themes, and size features themes.
- Mesh feature themes affect the plots of mesh cells. Themes include:
-
"Points" 0D cells 
"Lines" 1D cells, wireframe 
"Polygons" 2D cells - Rendering feature themes affect the rendering of meshes. Themes include:
-

"SampledPoints" sampled points from mesh cells 
"SphereAndTube" points as spheres and lines as tubes 
"SmoothShading" smooth shading 
"FaceNormals" normal for each 2D cell 
"LargeMesh" optimized for large number of cells - Style and other specifications for cells are effectively applied in the order MeshCellStyle, Style, and other wrappers, with later specifications overriding earlier ones.
- Label style and other specifications for cell labels are effectively applied in the order MeshCellLabel and Labeled, with later specifications overriding earlier ones.
- MeshRegion can be used with functions such as RegionMember, RegionDistance, RegionMeasure, and NIntegrate.
Examples
open all close allBasic Examples (6)
A 1D (curve) mesh region in 1D:
Label each point with its index:
A 1D (curve) mesh region in 2D:
Label each point with its index:
A 2D (surface) mesh region in 3D with each point labeled by its index:
A 3D (volume) mesh region in 3D with points labeled by its index:
A mesh region containing cells of mixed dimensions:
A volume mesh region in 3D from DelaunayMesh:
Scope (41)
Regions in 1D (3)
A strictly 0D MeshRegion is a point set:
Label the points with HighlightMesh:
A strictly 1D MeshRegion is a collection of line segments:
Label the segments with HighlightMesh:
A MeshRegion can combine elements of different dimensions:
Separate them with DimensionalMeshComponents:
Regions in 2D (4)
A strictly 0D MeshRegion is a point set:
Label the points with HighlightMesh:
A strictly 1D MeshRegion is a collection of line segments:
Label the segments with HighlightMesh:
A strictly 2D MeshRegion is a collection of polygonal faces:
Label the faces with HighlightMesh:
A MeshRegion can combine elements of different dimensions:
Separate them with DimensionalMeshComponents:
Regions in 3D (5)
A strictly 0D MeshRegion is a point set:
Label the points with HighlightMesh:
A strictly 1D MeshRegion is a collection of line segments:
Label the segments with HighlightMesh:
A strictly 2D MeshRegion is a collection of polygonal faces:
Label the faces with HighlightMesh:
A strictly 3D MeshRegion is a collection of polyhedral volumes:
Polyhedral volume cells include Tetrahedron, Prism, Pyramid, and Hexahedron:
A MeshRegion can combine elements of different dimensions:
Presentation (11)
MeshCellLabel can be used to label the parts of a MeshRegion:
The labels do not have to be strings:
Labeled can be used as a wrapper to label cells when constructing a MeshRegion:
The labels do not need to be strings:
MeshCellMarker can be used to mark parts of a MeshRegion:
MeshCellStyle can be used to set the Style of components of a MeshRegion:
Style can be used as a wrapper to style cells when constructing a MeshRegion:
Use a theme to draw 1D cells or a wireframe:
Use a theme to draw sampled points from mesh cells:
Region Properties (8)
Measure is ArcLength for a 1D mesh, Area for a 2D mesh, and Volume for a 3D mesh:
Compute and visualize the centroids of each:
A MeshRegion is always bounded:
Integrate over a MeshRegion:
Mesh Properties (10)
MeshCellCount returns the number of cells matching a given dimension or cell specification:
When no cell specification is given, the value for each dimension is returned:
MeshCells returns the cells in the mesh matching a given dimension or cell specification:
Individual cell indices or sets of cell indices can be used:
MeshCellIndex gets the index of a cell or set of cells in a mesh:
MeshCoordinates gets the coordinates of the mesh:
This list of coordinates is what the MeshCells refer to:
MeshPrimitives returns the primitives that make up the mesh:
Individual cell indices or sets of cell indices can be used:
DimensionalMeshComponents separates out components of a mesh with different dimensions:
ConnectedMeshComponents separates out components of a mesh based on connectivity:
MeshCellMeasure can be used to get the measures of a set of cells in a mesh:
The appropriate measure is used for each dimension:
MeshCellCentroid can be used to get the centroids of a set of cells in a mesh:
MeshCellQuality can be used to get the quality of a set of cells in a mesh:
Options (114)
AlignmentPoint (1)
Specify the position to be aligned in 3D Inset, using ![]() coordinates:
coordinates:
AspectRatio (1)
Use numerical values for AspectRatio:
AxesEdge (2)
AxesStyle (2)
BaselinePosition (3)
Align the center of a graphic with the baseline of the text:
Specify the baseline of a graphic as a fraction of the height by using Scaled:
BoxRatios (2)
FaceGrids (4)
FrameLabel (2)
FrameTicks (3)
FrameTicksStyle (2)
GridLines (3)
ImageMargins (3)
Allow no margins outside of ImageSize:
ImagePadding (4)
ImageSize (3)
Lighting (4)
MeshCellHighlight (3)
MeshCellHighlight allows you to specify highlighting for parts of a MeshRegion:
By making faces transparent, the internal structure of a 3D MeshRegion can be seen:
MeshCellLabel (3)
MeshCellLabel can be used to label parts of a MeshRegion:
Label the vertices and edges of a polygon:
MeshCellMarker (1)
MeshCellMarker can be used to assign values to parts of a MeshRegion:
Use MeshCellLabel to show the markers:
MeshCellShapeFunction (2)
MeshCellShapeFunction allows you to specify functions for parts of a MeshRegion:
MeshCellStyle (3)
MeshCellStyle allows you to specify styling for parts of a MeshRegion:
By making faces transparent, the internal structure of a 3D MeshRegion can be seen:
PlotLabel (2)
Display a label on the top of the graphic in TraditionalForm:
Use Style and other typesetting functions to modify how the label appears:
PlotRange (3)
PlotRangeClipping (2)
PlotRangePadding (3)
Include 1 coordinate unit of padding on all sides:
Include padding using Scaled coordinates:
PlotRegion (3)
The contents of a graphic use the whole region:
Limit the contents of the graphic to the middle half of the region in each direction:
ImagePadding can also be used to add padding around a graphic:
PlotTheme (9)
Feature Themes (7)
RotateLabel (2)
SphericalRegion (2)
Make a sequence of images be consistently sized, independent of orientation:
Without SphericalRegion, each image is made as big as possible:
Ticks (3)
TicksStyle (2)
ViewPoint (3)
ViewRange (2)
Applications (9)
Curves (4)
Extract the lines from a MeshRegion to make a wireframe mesh:
The indices given in MeshCells correspond to MeshCoordinates:
Compute the perimeter of a regular polygon:
The perimeter approaches ![]() as the number of sides goes to infinity:
as the number of sides goes to infinity:
Create a mesh region of a Koch curve using a Lindenmayer system:
Define a function for interpreting characters in the production string to coordinates using turtle graphics:
Initial parameters for interpreting the production string:
Compute coordinates of the Koch curve from the production string:
Generate mesh regions from the coordinates:
Find a formula for the length of the Koch curve at iteration ![]() :
:
Convert a graph to a MeshRegion:
You can compute with these as geometric regions:
You can still compute with them:
You can, for instance, compute the curve integral across these curves:
Surfaces (3)
Create a surface mesh by extruding a 2D curve mesh:
Some examples with planar layouts:
You can compute with the resulting regions, in this case computing surface integrals:
Directly generate a rectangular grid mesh. Here IndexFlatten flattens out the position index in the same way that Flatten would flatten it:
Alternatively, generate the same mesh region as the product of 1D meshes:
Generalize the direct method above to generate a mesh region corresponding to a pattern matrix:
Volumes (2)
Directly generate a rectangular grid mesh. Here IndexFlatten flattens out the position index in the same way that Flatten would flatten it:
Alternatively, generate the same mesh region as the product of 1D meshes:
Generalize the direct method above to generate a mesh region corresponding to a pattern matrix:
Use the idea above to construct a Seidel mesh, i.e. a mesh region with tunnels going in every direction without crossing:
By converting to a boundary mesh and styling it, it becomes easier to comprehend:
Properties & Relations (9)
MeshRegion can have any geometric dimension:
MeshRegion is always bounded:
Use BoundedRegionQ to test and RegionBounds for actual bounds:
MeshRegionQ can be used to test whether a region is a MeshRegion:
Use DelaunayMesh to create a MeshRegion from a set of points:
Use TriangulateMesh to convert a BoundaryMeshRegion to a MeshRegion:
Use DiscretizeRegion to convert any region to MeshRegion:
Use DiscretizeGraphics to convert Graphics to MeshRegion:
Use Show to convert any MeshRegion to Graphics:
MeshRegion is usually more memory intensive than BoundaryMeshRegion:
Text
Wolfram Research (2014), MeshRegion, Wolfram Language function, https://reference.wolfram.com/language/ref/MeshRegion.html (updated 2022).
CMS
Wolfram Language. 2014. "MeshRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/MeshRegion.html.
APA
Wolfram Language. (2014). MeshRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeshRegion.html
BibTeX
@misc{reference.wolfram_2025_meshregion, author="Wolfram Research", title="{MeshRegion}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/MeshRegion.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_meshregion, organization={Wolfram Research}, title={MeshRegion}, year={2022}, url={https://reference.wolfram.com/language/ref/MeshRegion.html}, note=[Accessed: 06-January-2026]}