NContourIntegrate

NContourIntegrate[f,z∈cont]

gives the numerical integral of f along the contour defined by cont in the complex plane.

Details and Options

  • Contour integration is also known as path integration or complex line integration.
  • Contour integrals arose in the study of holomorphic and meromorphic functions in complex analysis, but they are now used in a wide range of applications, including the computation of inverse Laplace transforms and Z transforms, definite integrals and sums, and solutions of partial differential equations.
  • The contour integral of a function 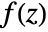along a contour cont 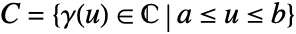is given by:
  • The value of the contour integral is independent of the parametrization, but it does depend on the orientation of the contour cont.
  • The function f is typically a meromorphic function of z, but it can be any piecewise continuous function that is defined in a neighborhood of cont in the complex plane.
  • The contour integral of a meromorphic function 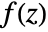along a closed contour cont can be computed using Cauchy's residue theorem.
  • Commonly used closed contours cont include: »
  • {"Hairpin",hl}encircle a half-line hl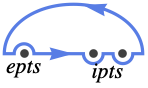
    {"UpperSemicircle",ipts,epts}encircle the upper half-plane, including the points ipts and excluding the points epts, all on the real axis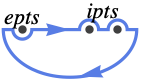
    {"LowerSemicircle",ipts,epts}encircle the lower half-plane, including the points ipts and excluding the points epts, all on the real axis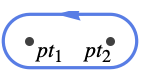
    {"Dumbbell",pt1,pt2}encircle the capsule given by points pt1 and pt2
  • The complex points are given as {x,y} pairs; complex half-lines are given as HalfLine primitives.
  • A contour cont in 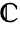can also be specified as a curve region (RegionQ) in .
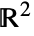  • For a parametric contour ParametricRegion[{x[t],y[t]},{{t,a,b}}], the orientation is in the direction of increasing t.
  • Special contours in and their assumed orientations:
  • Line[{p1,p2,…}]from p1 to p2 etc.
    HalfLine[{p1,p1}]from p1 toward p2
    InfiniteLine[{p1,p2}]from p1 toward p2
    Circle[p,…]counterclockwise
  • Area regions such as Polygon can be used, and the contours are then taken to be the boundary contours RegionBoundary[Polygon[…]].
  • Special area regions in and their assumed boundary contour orientations:
  • Triangle[{p1,p2,p3}]counterclockwise
    Rectangle[p1,p2]counterclockwise
    RegularPolygon[n,…]counterclockwise
    Polygon[{p1,p2,…}{{q1,q2,…},…}]counterclockwise of the outer contour, clockwise for inner contours
    Disk[p,…]counterclockwise
    Ellipsoid[p,…]counterclockwise
    StadiumShape[{p1,p2},r]counterclockwise
    Annulus[p,{rm,rm},…]counterclockwise for outer contour and clockwise for inner contour
  • The regions in cont may be wrapped with Inactive to prevent auto-evaluation.
  • The following options can be given:
  • AccuracyGoal Automaticdigits of absolute accuracy sought
    MaxPoints Automaticmaximum total number of sample points
    MaxRecursion Automaticmaximum number of recursive subdivisions
    Method Automaticmethod to use
    MinRecursion 0minimum number of recursive subdivisions
    PrecisionGoal Automaticdigits of precision sought
    WorkingPrecision Automaticthe precision used in internal computations

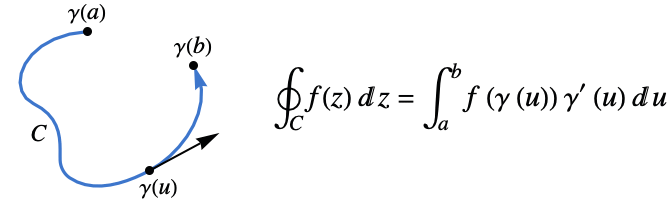
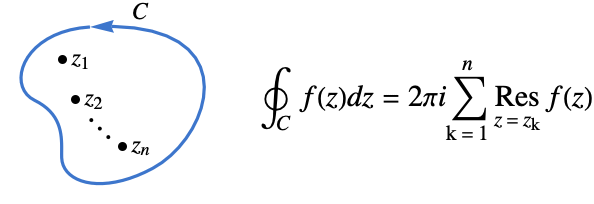
Examples

open allclose all

Basic Examples  (3)

Integrate 1/z along the unit circle:

Integrate a rational function along a circle with a center at the origin and radius 2:

Integrate a meromorphic function along an elliptical contour:

Compare the result with ContourIntegrate:

Scope  (46)

Basic Uses  (9)

Contour integral over a circular path:

Compare to ContourIntegrate:

Contour integral over a polygonal chain in the complex plane:

Contour integrate over a half-disk:

Numerical contour integral of a trigonometric expression:

Contour integral over a parametric contour in the complex plane:

Contour integral of a meromorphic function over a closed semicircle:

Contour integral of a function with an essential singularity:

Contour integral of a non-analytic function:

Contour integral of a function containing a branch cut:

Special Topic: Rational Functions  (8)

Integrate a rational function along a circle:

Integrate a rational function along a pentagonal contour:

Contour integral of a rational function along a triangular path:

Contour integral of a rational function along a rectangular path:

Contour integral along the unit circle:

Contour integral over an open polygonal chain:

Contour integral over an open arc:

Contour integral of a rational function along a circular path:

Special Topic: Meromorphic Functions  (5)

Contour integral of a meromorphic function along a polygonal path:

Evaluate the contour integral symbolically:

Contour integral along an elliptical path:

Contour integral over a closed semicircle:

Contour integral over a sector of annulus:

Contour integral over a circle of radius 6:

Special Topic: Functions with Essential Singularities  (4)

Exponential function:

Sin function with an essential singularity inside the contour:

Contour integral of a function with an essential singularity:

Essential singularity arising from a periodic function:

Special Topic: Non-analytic Functions  (4)

Contour integral over a circular path:

Contour integral of the Arg function:

Contour integral over an elliptic sector:

Contour integral over a rectangular path:

Special Topic: Functions with Branch Cuts  (2)

Contour integral of a piecewise continuous function:

Contour integral of a function with branch cuts on the integration path:

Special Topic: Named Contours  (7)

Contour integral along the real axis in a positive direction, around poles on the real axis, closing in the upper half of the complex plane:

A second example:

Contour integral along the real axis in a positive direction, around poles on the real axis, closing in the lower half of the complex plane:

By default, this contour is traversed clockwise.

A second example:

Contour integral around a hairpin or Hankel contour:

Integral around a hairpin or Hankel contour:

Compare to the symbolic evaluation:

Contour integral that evaluates to a Zeta function:

Numerical evaluation:

Hairpin or Hankel contour:

Dumbbell contour around the branch cut, joining 0 and 1:

Special Topic: Region Contours  (7)

Contour integral over an infinite line:

Contour integral over a circular contour:

Contour integral over a line segment:

Contour integral over a triangular path:

Contour integral over a rectangular path:

Contour integral over a sector:

Contour integral over an annulus:

Options  (7)

AccuracyGoal  (1)

The option AccuracyGoal sets the number of digits of accuracy:

The result with default settings only sets a PrecisionGoal:

MaxPoints  (1)

The option MaxPoints stops the integration after a specified number of points has been evaluated:

MaxRecursion  (1)

The option MaxRecursion specifies the maximum number of recursive steps:

Increasing the number of recursions:

The exact result is:

Method  (1)

The option Method can take the same values as in NIntegrate. For example:

With the default option:

Compare to the truncated exact result:

MinRecursion  (1)

The option MinRecursion forces a minimum number of subdivisions:

Compare to the exact result:

PrecisionGoal  (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision  (1)

Using WorkingPrecision, the working precision can be set:

Applications  (22)

Rational Functions  (2)

Contour integral on a half-disk of large radius:

It agrees with the limit for large computed symbolically:

The same result obtained with NIntegrate:

Integral over the real line:

This can be obtained as the limit of a contour integral:

Trig-Rational Products  (2)

Integrals on the real line:

These two results can be recovered using a complex integral along a half-disk of large radius:

Integrals on the real line:

Use a complex integral:

Trigonometric Functions  (3)

Integral of a rational function of the sine:

This can be recovered as a contour integral:

Integral of a rational function of the cosine:

This can be obtained as a contour integral:

Integral of a rational function of the sine:

As a contour integral:

Fourier Transform  (2)

Fourier transform of a function:

For positive :

Computation using a numerical contour integral:

For negative :

Fourier transform of a function:

Computation using a contour integral: for positive :

For negative :

Inverse Laplace Transform  (4)

Inverse Laplace transform of a function:

For :

Computation using a contour integral:

Inverse Laplace transform of a logarithm of a rational function:

For :

Using a contour integral:

Inverse Laplace transform of a function containing a square root:

For :

The same computation using a contour integral:

Inverse Laplace transform of a function containing Log:

For :

Use the definition of the inverse Laplace transform:

Inverse Mellin Transform  (4)

Inverse Mellin transform of a function:

For :

Compute it from a contour integral:

Inverse Mellin transform of a function:

For :

Compute it from its definition as a contour integral:

Mellin transform of a function:

Recover the function at using an inverse Mellin transform:

This is the same as:

Mellin transform of a rational function:

Recover the function at using an inverse Mellin transform:

Inverse Z Transform  (2)

Inverse Z transform of a function:

For :

Obtain the result from its definition as a contour integral:

Inverse Z transform of a function:

For :

From its definition as a contour integral of large radius:

Classical Theorems  (3)

Residue theorem applied to the contour integral of a meromorphic function over a closed path:

The integral is equal to times the sum of the residues of the poles inside the contour:

The integration contour can be deformed without changing the value of the integral, provided that no singularities of the function are crossed:

If no singularities lie inside the contour, the integral is zero:

Properties & Relations  (6)

Apply N[ContourIntegrate[…]] to obtain a numerical solution if the symbolic calculation fails:

This can also be computed using NIntegrate:

It can also be computed with NContourIntegrate:

Numerical contour integrals can also be obtained using NIntegrate:

This is equivalent to:

NIntegrate can integrate along a straight contour in the complex plane:

This is equivalent to:

Contour integrals over a closed path can also be obtained using ResidueSum:

Poles of a meromorphic function can be found using FunctionPoles:

The integral can also be computed using Residue:

Contour integrals over a closed path can also be obtained using Residue:

Interactive Examples  (2)

Contour integral over a sector of varying radius:

Compare with ContourIntegrate:

Another contour integral over a sector of varying radius:

Compare with ContourIntegrate:

Wolfram Research (2024), NContourIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/NContourIntegrate.html.

Text

Wolfram Research (2024), NContourIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/NContourIntegrate.html.

CMS

Wolfram Language. 2024. "NContourIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NContourIntegrate.html.

APA

Wolfram Language. (2024). NContourIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NContourIntegrate.html

BibTeX

@misc{reference.wolfram_2024_ncontourintegrate, author="Wolfram Research", title="{NContourIntegrate}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NContourIntegrate.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ncontourintegrate, organization={Wolfram Research}, title={NContourIntegrate}, year={2024}, url={https://reference.wolfram.com/language/ref/NContourIntegrate.html}, note=[Accessed: 05-November-2024 ]}