NeumannValue

NeumannValue[val,pred]

表示一个 Neumann 边界值 val，被指定为位于赋给 NDSolve 的区域的边界上 pred 为 True 的部分.

更多信息

  • NeumannValue 被用在偏微分方程中，用来指定诸如 DSolve 和 NDSolve 这样的函数中的边界值.
  • 在 NDSolve[eqns,{u1,u2,…},{x1,x2,…}∈Ω] 中，xi 为独立变量，uj 是因变量，Ω 是边界为 ∂Ω 的区域.
  • 以绿色显示 Neumann 值有可能被指定的位置. 它们出现在区域 Ω 的边界 ∂Ω 上，并在边界外向法线的方向上指定了通量.
  • ∇·(-c ∇u-α u+γ)+…=f-NeumannValue[g-q u,pred] 用于指定边界 ∂Ω 中 pred 为真的部分的通量，使得 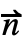·(c ∇u+α u-γ)=g-q u 成立. 在 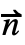·(c ∇u+α u-γ)=g-q u 中的系数 c、α 和 γ 通过由∇·(-c ∇u-α u+γ)+β·∇u+a u=f-NeumannValue[g-q u,pred] 给出的 PDE 隐式定义. 是 ∂Ω 的外向单位法线. 系数 g 和 q 可依赖于任意自变量 {x1,x2,…}.
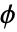  • 对于有限元近似法，PDE 与测试函数 相乘，并在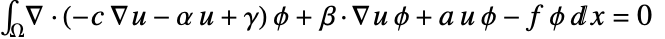
    .
    上积分. 分部积分给出 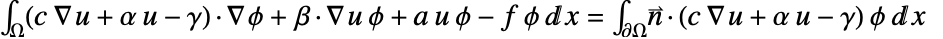. 边界积分中的被积式 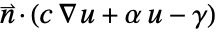被 NeumannValue 代替，产生方程 .»
  • 有限元近似法中，Neumann 值被强制作为每个 pred 为 True 的 ∂Ω 的离散化边界元素上的积分条件. 一维情况下，边界元素为点，二维情况下，边界元素为边，三维情况下，边界元素为面.
  • 如果边界 ∂Ω 的某些部分没有被边界条件指定，则该部分的通量 ∇·(-c ∇u-α u+γ)+… 被认为是 f=f-0=f-NeumannValue[0,…]，所以不指定任何边界条件等价于 Neumann 0 条件.
  • 方程右侧的正的 NeumannValue 模拟了进入域的通量.
  • 任何自变量 x1,… 的等式和不等式的逻辑组合都可用于谓词 pred.
  • NeumannValue 可用来指定 Neumann 和 Robin 边界条件：
  • ·(c ∇u+α u-γ)=0
    		• 自然边界条件 (Neumann 0) 没有指定边界条件或 NeumannValue[0,pred]
  • ·(c ∇u+α u-γ)=g
    		• NeumannNeumannValue[g,pred]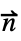
  • ·(c ∇u+α u-γ)=g-q u
    		• Robin （广义 Neumann）NeumannValue[g-q u,pred]
  • ·(c ∇u+α u-γ)=g-h(u)
    		• 广义非线性 NeumannNeumannValue[g-h[u],pred]
  • 对于系统， ∇·∑j(-cj∇uj-αjuj+γ)+…f+NeumannValue[g-∑jqjuj]+… 对应于条件 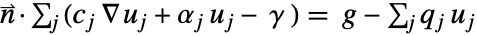在区域边界上 pred 为 True 的部分上被满足.
  • 对于含时方程，val 和 pred 都有可能依赖于时间.
  • NeumannValue 和 Derivative 在偏微分方程中的作用和意义略有不同. »
  • 对于有限元近似法，在一维情况下，NeumannValue 在结点上进行操作；二维情况下，在边上进行操作；三维情况下，则在面上进行操作.
  • 不应在边界的同一部分上同时指定 DirichletCondition 和 NeumannValue.
  • 几个 NeumannValue 可能会在边界上重叠. »

范例

打开所有单元关闭所有单元

基本范例  (1)

Dirichlet 和 Neumann 边界条件为： ，； ，，在圆盘上求解拉普拉斯方程 ：

范围  (4)

求解线段上的非线性方程 ，当 的广义 Neumann 条件 ，当 的 Dirichlet 条件 ：

验证分析解的数值解:

求解具有曲线边上非线性广义 Neumann 边界条件的 PDE：

可视化解：

在边界的同一部分可能存在多个 NeumannValue：

注意 处的扭结，在 下面的部分，NeumannValue 的两种情况同时存在，而在 上面的部分，只有一个 NeumannValue 存在.

NeumannValue 可用于近似一个 DirichletCondition.

求解带有两个 DirichletCondition 实例和 Dirichlet 值的参数 的 PDE：

求解同样的 PDE，其中，DirichletCondition 被缩放的广义 NeumannValue 替代：

检查解之间的不同：

这种用 NeumannValue 逼近 DirichletCondition 的方法，仅当 Dirichlet 条件和 Neumann 值需要在边界的同一段上调整时才可以使用.

应用  (12)

一维问题  (2)

Dirichlet 边界条件为 ，Robin 边界条件为 ，在单位长度上求解 ：

比较数值解和解析解：

Dirichlet 边界条件为 ，Robin 边界条件为 ，在单位长度上求解 ：

比较 的值与 处规定的 Dirichlet 边界条件值 1 的差别：

比较 的值与 处规定的 Robin 边界条件 的差别：

由于这是积分条件，条件满足的程度取决于网格. 使用更精细的网格给出更好的结果：

二维问题  (2)

用边界指定一个区域：

显示区域及边界：

根据红色和蓝色边界上的温度以及绿色边界上的通量求解拉普拉斯方程：

Neumann 边界条件可用于探索区域的对称性. 指定一个有洞的区域：

指定拉普拉斯算子：

在内边界上设置 Dirichlet 条件 ，在外边界上设置 ：

在区域上求解方程并图示结果：

指定一个对称子区域：

对于没有明确规定条件的边界，假设为零 Neumann 条件：

三维问题  (1)

Neumann 边界条件为 ，在单位球面上求解 ：

含时问题  (4)

根据初始条件和边界条件求解含时问题：

求解反射边界条件下的波动方程：

求解吸收边界条件下的波动方程：

求解吸收边界条件下的波动方程. 注意 Neumann 值是 的一阶时间导数：

查看波被吸收的量随时间变化的情况：

耦合系统的边界条件  (3)

指定耦合方程组：

根据左边的两个 Dirichlet 条件和右边的两个 Neumann 条件解方程组.

画出解：

指定耦合微分方程组：

指定 Dirichlet 和 Neumann 边界条件并解方程组：

画出解：

将计算结果和解析解进行比较：

绘制数值解和解析解之间的误差：

指定计算一个板条上的平面应力的算子，其中包含杨氏模数和泊松比：

板条的左边固定不动，右边沿负 方向施加一个边界载荷.

绘制板条上沿 方向的变形等值线图：

绘制板条上沿 方向的变形等值线图：

图示板条变形的情况：

属性和关系  (1)

这一部分我们来讨论设置区域内的边界条件如何影响解. 域是来自 的区域，在 处有内部边界. 为此创建一个有限元边界网格，其节点位于 、 和 ：

创建完整的网格：

为了说明内部边界处不同边界条件的行为，我们选择了扩散型方程，其中，扩散系数 ：

作为边界条件，在域的左右端设置特定值：

在第一个例子中，设 PDE 等于 0. 即，在内部的点 处没有其他相互作用. 这是默认行为：

默认行为与在 处设置 Neumann 值为 0 相同：

默认行为所得的解与将 Neumann 值设为零得到的解之间的差为零；它们是完全相同的解：

下面，设 处的值为 ：

从绘图中可以看出因变量 在 处的值为 ：

在接下来的实验中，设 处的 Neumann 值为 . 我们不清楚这意味着什么，因为不清楚法线

    • 实际上指向哪个方向，因为没有内部或外部. 但是仍可以计算通量不连续情况的解：

    下面的图比较了各种内部边界条件：

    更进一步，可以通过设置 使扩散系数在内部材料边界处不连续：

    也可以翻转边界条件的值.

    可能存在的问题  (4)

    仅指定 Neumann 边界条件可能导致非唯一解. 有些情况下，可能根本无解：

    指定 Robin 边界条件则足够定解方程：

    Dirichlet 和 Neumann 边界条件为 处 ， 处，，求解在矩形上扩散系数 的拉普拉斯方程 ：

    验证解与右手侧的 Neumann 值是一致的：

    注意，设扩散系数 来解拉普拉斯方程 ，使得 Neumann 值变为 ：

    验证解与右手侧的 Neumann 值也是一致的：

    可视化两个解：

    没有为边界的某些部分指定边界条件，则表示此处为自然边界条件 ：

    这里给出的是同一个边界条件：

    有时，导入的网格甚至生成的网格都可能存在数值不精确的情况. 例如，一个预定区域是一个矩形 ，但该区域的离散化版本不精确，因此实际上是 . 在这种情况下，如果指定了 形式的谓词，就会生成一条错误信息，因为 并不存在. 请看以下构建的范例：

    处理这种情况的一种方法是将谓词表述为边界 ，其中 是边界的粗细：

    这种技术也可用于更复杂的谓词，如边界的圆形部分，在这种情况下，数字精度问题更有可能出现.

    Wolfram Research (2014)，NeumannValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NeumannValue.html （更新于 2023 年）.

    文本

    Wolfram Research (2014)，NeumannValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NeumannValue.html （更新于 2023 年）.

    CMS

    Wolfram 语言. 2014. "NeumannValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/NeumannValue.html.

    APA

    Wolfram 语言. (2014). NeumannValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NeumannValue.html 年

    BibTeX

    @misc{reference.wolfram_2024_neumannvalue, author="Wolfram Research", title="{NeumannValue}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/NeumannValue.html}", note=[Accessed: 21-November-2024 ]}

    BibLaTeX

    @online{reference.wolfram_2024_neumannvalue, organization={Wolfram Research}, title={NeumannValue}, year={2023}, url={https://reference.wolfram.com/language/ref/NeumannValue.html}, note=[Accessed: 21-November-2024 ]}