PoissonDistribution
平均 μ のポアソン(Poisson)分布を表す.
詳細
- ポアソン分布における整数値
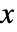 の確率は,
の確率は,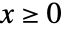 のとき
のとき 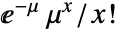 であり,
であり,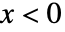 のときはゼロである. »
のときはゼロである. » - PoissonDistributionでは,μ は任意の正の実数でよい.
- PoissonDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- PoissonDistribution[μ]は,
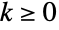 の整数値について定義され,正の実数母数 μ(分布の平均)によって決定される離散統計分布を表す.ポアソン分布は離散的で単峰性の確率密度関数(PDF)を持つ.この分布は,より一般的な Poisson–Consul分布 (PoissonConsulDistribution)と区別するために「古典的ポアソン分布」と呼ばれることがある.Poisson–Consul分布の方は「一般化」ポアソン分布と呼ばれることがある.
の整数値について定義され,正の実数母数 μ(分布の平均)によって決定される離散統計分布を表す.ポアソン分布は離散的で単峰性の確率密度関数(PDF)を持つ.この分布は,より一般的な Poisson–Consul分布 (PoissonConsulDistribution)と区別するために「古典的ポアソン分布」と呼ばれることがある.Poisson–Consul分布の方は「一般化」ポアソン分布と呼ばれることがある. - ポアソン分布の起源はフランス人の数学者であるアブラーム・ド・モアブル(Abraham de Moivre)の1711年の論文まで遡ることができる.しかし,この分布の名前はフランス人の数学者であるシメオン・ポアソン(Siméon Poisson)に因んだものである.これは,ポアソンが1830年代の後半にこの分布を使って不当な有罪判決をモデル化したためである.もともと,ポアソン分布は,ある事象がその前に起こってから時間とは独立で既知の平均的な割合で起こる場合にその事象の単位時間当たりの生起尤度を与えるものである.これを導出するために使われるテクニックのため,この分布は一定ではあるが生起確率が非常に低い多数の独立な試行からなる状況(例:1年間に馬に蹴られて死ぬ騎馬兵の数)のモデル化に非常に有効だった.ポアソン分布は,インターネットトラフィック,受信電話数,スポーツイベントでの得点等を含む現代のさまざまな現象のモデル化に使われており,金融,生物学,物理学,電気通信等の分野で貴重なモデリングツールとなっている.
- RandomVariateを使って,ポアソン分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,PoissonDistribution[μ]](より簡略な表記では xPoissonDistribution[μ])を使って,確率変数 x がポアソン分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[PoissonDistribution[μ],x]およびCDF[PoissonDistribution[μ],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合がポアソン分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックポアソン分布を推定することが,FindDistributionParametersを使ってデータをポアソン分布にフィットすることができる.ProbabilityPlotを使って記号ポアソン分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ポアソン分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたポアソン分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってポアソン分布を含む高次元分布を構築することが,ProductDistributionを使ってポアソン分布を含む独立成分分布の結合分布を計算することができる.
- PoissonDistributionは他の数多くの統計分布と関連している.この分布は,PoissonDistribution[μ]の確率密度関数がPoissonConsulDistribution[μ,0]のそれと厳密に等しいという意味で,PoissonConsulDistributionによって一般化される.さらに,n→∞のときのBinomialDistribution[n,μ/n]の確率密度関数がPoissonDistribution[μ]の確率密度関数と厳密に等しく,PolyaAeppliDistribution[θ,p]の確率密度関数は p→0のときにPoissonDistribution[θ]の確率密度関数に近付く傾向があるという意味で,PoissonDistributionはBinomialDistributionとPolyaAeppliDistributionの両方の極限のケースである.PoissonDistributionはNegativeBinomialDistribution,GammaDistribution,GeometricDistribution,ExponentialDistribution,BorelTannerDistribution,BinomialDistribution,NegativeMultinomialDistribution,MultinomialDistributionとも関連している.
例題
すべて開くすべて閉じるアプリケーション (14)
PoissonDistributionのCDFは右連続関数の例である:
ある都市における事故の平均発生件数は1日100件である.毎日の事故のシミュレーションを行う:
5秒間にバケツに落ちる雨滴の予想数は20滴である.5秒ごとの雨滴の数のシミュレーションを行う:
放射性物質は平均で1秒間に3.2個の ![]() 粒子を放出する.その分布を示す:
粒子を放出する.その分布を示す:
1秒間に放出される粒子の標準的な数を10分間の範囲でシミュレーションする:
ベニヤ板には50平方フィートにつき平均1つの傷があるとする.1平方フィートを単位として傷を見付けるシミュレーションを行う:
4フィート掛ける8フィートのベニヤ版に傷がない確率を求める:
面積が7.54 cm![]() の鏡に傷が全くない確率は0.9100である.同じ研磨方法で面積が19.50 cm
の鏡に傷が全くない確率は0.9100である.同じ研磨方法で面積が19.50 cm![]() の鏡を作る.ポアソンの誤差過程を仮定して大きい鏡に傷がない確率を求める.小さい鏡の条件と誤差分布PoissonDistribution [λ area]を使用する:
の鏡を作る.ポアソンの誤差過程を仮定して大きい鏡に傷がない確率を求める.小さい鏡の条件と誤差分布PoissonDistribution [λ area]を使用する:
結果として得られる鏡の研磨による傷の分布は以下の通りである:
書籍の誤植はポアソン過程に従ってランダムに起る.384ページで158ヶ所の誤植がある.分布がPoissonDistribution[λ p]に従っているとして,1ページあたりの誤植の分布を求める.ただし,p はページ数である:
医薬品の副作用のモデリングで10万人に2人の割合で副作用が発生することが分かった.ポアソン分布を仮定して副作用の分布を求める:
この薬が35万人に処方された場合に少なくとも5件の副作用が発生する確率を求める:
コールセンターに ![]() 秒間に寄せられるクエリの数
秒間に寄せられるクエリの数 ![]() は母数
は母数 ![]() のポアソン分布に従っている.ただし,
のポアソン分布に従っている.ただし,![]() は1秒間のクエリの平均到着率である.平均到着率が毎分4クエリであると仮定して10秒間に4より多くのクエリが届く確率を求める:
は1秒間のクエリの平均到着率である.平均到着率が毎分4クエリであると仮定して10秒間に4より多くのクエリが届く確率を求める:
マルチプレクサーで ![]() 秒間に届くパケット数
秒間に届くパケット数 ![]() は母数
は母数 ![]() のポアソン分布に従っている.ただし,
のポアソン分布に従っている.ただし,![]() は1秒間のパケットの平均到着率である.
は1秒間のパケットの平均到着率である.![]() 秒間にパケットが全く届かない確率を求める:
秒間にパケットが全く届かない確率を求める:
データセンターには10000のディスクドライブがある.1日にディスク障害が起きる確率を![]() として,ディスク障害が全く起らない日の確率を求める:
として,ディスク障害が全く起らない日の確率を求める:
一日にディスク障害のあったドライブを99.9%の割合で取り替えるためにはスペアのディスクドライブがいくつ必要かを求める:
ある液晶ディスプレイの画素数は1920×1080である.問題のある画素が15以下のディスプレイが合格となる.生産段階で画素に問題が発生する確率は![]() である.合格するディスプレイの割合を求める:
である.合格するディスプレイの割合を求める:
4000×2000画素のディスプレイの生産で合格率が少なくとも90%になるために必要な問題画素の発生率を求める:
1分間に平均100回受信する交換台がある.キャパシティを超えるのが60分間で1回未満になるためにはこの交換台のキャパシティがどれほどでなければならないかを求める:
光通信システムでは透過光が受信機で電流を生成する.電子の数は光のタイプによりポアソン分布と他の分布の母数混合分布に従う.光源が強度 ![]() の可干渉性のレーザー光線を使う場合,電子の数はポアソン分布に従う:
の可干渉性のレーザー光線を使う場合,電子の数はポアソン分布に従う:
これはPoissonDistributionである:
光源が熱照明を使う場合,ポアソン母数は母数![]() でExponentialDistributionに従い,電子数の分布は以下のようになる:
でExponentialDistributionに従い,電子数の分布は以下のようになる:
特性と関係 (11)
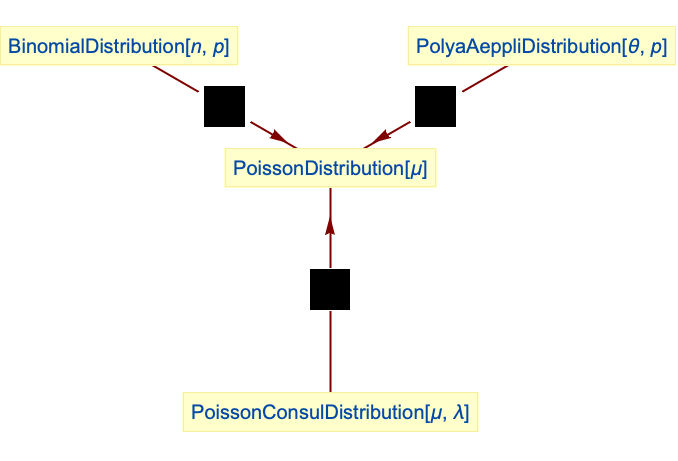
PoissonDistributionは ![]() のBinomialDistributionの極限のケースである:
のBinomialDistributionの極限のケースである:
PoissonConsulDistributionを簡約するとポアソン分布になる:
ポアソン分布はPolyaAeppliDistributionの極限のケースである:
NegativeBinomialDistributionはPoissonDistributionとGammaDistributionの混合分布である:
GeometricDistributionはPoissonDistributionとGammaDistributionの混合分布である:
ポアソン分布とExponentialDistribution母数混合分布はGeometricDistributionに従う:
PoissonConsulDistributionはBorelTannerDistributionとPoissonDistributionの母数混合分布に従う:
平均が固定されている場合のNegativeBinomialDistributionの極限はポアソン分布に従う:
μ の値が大きい場合,PoissonDistributionはNormalDistributionで近似することができる:
考えられる問題 (2)
テキスト
Wolfram Research (2007), PoissonDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/PoissonDistribution.html.
CMS
Wolfram Language. 2007. "PoissonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PoissonDistribution.html.
APA
Wolfram Language. (2007). PoissonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonDistribution.html