SingularValuePlot
SingularValuePlot[lsys]
generates a plot of the singular values of the transfer function for the system lsys.
SingularValuePlot[lsys,{ωmin,ωmax}]
plots for the frequency range ωmin to ωmax.
SingularValuePlot[expr,{ω,ωmin,ωmax}]
plots expr using the variable ω.
Details and Options
- The system lsys can be TransferFunctionModel or StateSpaceModel, including descriptor and delay systems.
- For a system lsys with the corresponding transfer function
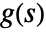, the following expressions are plotted: -
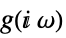
continuous-time system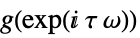 
discrete-time system with sample time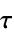 
- SingularValuePlot treats the variable ω as local, effectively using Block.
- SingularValuePlot has the same options as Plot, with the following additions and changes: [List of all options]
-
SamplingPeriod None the sampling period ScalingFunctions {"Log10","dB"} the scaling functions Tolerance 0 the tolerance in computing the singular values - The scaling functions can be specified as ScalingFunctions->{freqscale,magscale}.
- The frequency scale freqscale can be "Log10" or "Linear", which correspond to the base-10 logarithmic scale and linear scale, respectively.
- The magnitude scale magscale can be "dB" or "Absolute", which correspond to the decibel and absolute values of the magnitude, respectively.
-
AlignmentPoint Center the default point in the graphic to align with AspectRatio 1/GoldenRatio ratio of height to width Axes True whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ClippingStyle None what to draw where curves are clipped ColorFunction Automatic how to determine the coloring of curves ColorFunctionScaling True whether to scale arguments to ColorFunction ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool Epilog {} primitives rendered after the main plot EvaluationMonitor None expression to evaluate at every function evaluation Exclusions Automatic points in x to exclude ExclusionsStyle None what to draw at excluded points Filling None filling to insert under each curve FillingStyle Automatic style to use for filling FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelingSize Automatic maximum size of callouts and labels LabelStyle {} style specifications for labels MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh None how many mesh points to draw on each curve MeshFunctions {#1&} how to determine the placement of mesh points MeshShading None how to shade regions between mesh points MeshStyle Automatic the style for mesh points Method Automatic the method to use for refining curves PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotHighlighting Automatic highlighting effect for curves PlotLabel None overall label for the plot PlotLabels None labels to use for curves PlotLayout Automatic how to position curves PlotLegends None legends for curves PlotPoints Automatic initial number of sample points PlotRange {Full,Automatic} the range of y or other values to include PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to specify the style for each curve PlotTheme $PlotTheme overall theme for the plot PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RegionFunction (True&) how to determine whether a point should be included RotateLabel True whether to rotate y labels on the frame SamplingPeriod None the sampling period ScalingFunctions {"Log10","dB"} the scaling functions TargetUnits Automatic units to display in the plot Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks Tolerance 0 the tolerance in computing the singular values WorkingPrecision MachinePrecision the precision used in internal computations
List of all options
Examples
open allclose allBasic Examples (3)
Scope (7)
SingularValuePlot shows all the singular values:
A one-input, two-output system:
A two-input, three-output system:
Generalizations & Extensions (1)
Options (16)
CoordinatesToolOptions (3)
PlotLegends (4)
Use automatic legends for multiple singular values:
Use a list of text for legends:
Use LineLegend to add a overall legend label:
PlotTheme (1)
SamplingPeriod (2)
Applications (1)
Wolfram Research (2010), SingularValuePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/SingularValuePlot.html (updated 2014).
Text
Wolfram Research (2010), SingularValuePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/SingularValuePlot.html (updated 2014).
CMS
Wolfram Language. 2010. "SingularValuePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/SingularValuePlot.html.
APA
Wolfram Language. (2010). SingularValuePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SingularValuePlot.html