Sum

Sum[f,{i,imax}]

総和 を評価する．

Sum[f,{i,imin,imax}]

i=i_(min)から開始する．

Sum[f,{i,imin,imax,di}]

di を刻み幅として使用する．

Sum[f,{i,{i1,i2,…}}]

連続する値 i_(1), i_(2), …を使用する．

Sum[f,{i,imin,imax},{j,jmin,jmax},…]

多重総和 を評価する．

Sum[f,i]

不定和分 を与える．

詳細とオプション

  • Sum[f,{i,imax}]は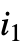sum_(i)^(i_(max))f と入力できる．
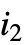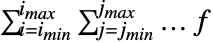  • sumはsum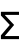あるいは\[Sum]と入力できる．
  • Sum[f,{i,imin,imax}]はsum_(i=i_(min))^(i_(max))f と入力できる．
  • 極限は，通常の入力ではsumの真下付き文字と真上付き文字であり，その他のテキストに含まれる場合は下付き文字と上付き文字である．
  • Sumは，Wolfram言語の標準的な反復の指定を使用する．
  • 反復変数 i は，Blockを使って実質的に局所的なものとして取り扱われる．
  • 総和の範囲が有限の場合，一般に には一連の値が割り当てられ，そのそれぞれについて が評価される．
  • 多重総和において，最も外側の変数の範囲が最初に与えられる． »
  • 総和の極限は数値である必要はなく，Infinityあるいは記号的な式でもよい． » »
  • 項の有限数を加算することで具体的に和を求めることができない場合，Sumは記号的な結果を求める．この場合，f はまず記号的に評価される．
  • 不定和分 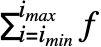は i に対するその差分が f を与えるものとして定義される． »
  • 不定和分と定和分は任意の順序で混ぜ合せることができる． »
  • 使用可能なオプション
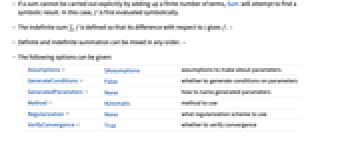
  • Assumptions $Assumptionsパラメータに関する仮定
    GenerateConditions Falseパラメータに関する条件を生成するかどうか
    GeneratedParameters None生成されたパラメータにどのように名前を付けるか
    Method Automatic使用するメソッド
    Regularization Noneどの正規化スキームを使うか
    VerifyConvergence True収束を確かめるかどうか
  • RegularizationにはNone，"Abel"，"Borel"，"Cesaro"，"Dirichlet"，"Euler"の値を使うことができる．{reg1,reg2,…}は多重和の異なる変数に異なるスキームを指定する．
  • Method->"method"は指定のメソッドを使って総和を出す．
  • Method->{"strategy",Method->{"meth1","meth2",…}}は指定の戦略メソッドで制御されたメソッド"methi"を使う．
  • 使用可能な戦略メソッド
  • "SequentialFirstToSucceed"成功するメソッドが見付かるまで各メソッドを順に試す
    "SequentialBestQuality"各メソッドを順に試し最もよい結果を返す
    "ParallelFirstToSucceed"成功するメソッドが見付かるまで各メソッドを同時に試す
    "ParallelBestQuality"各メソッドを同時に試し最もよい結果を返す
    "IteratedSummation"反復する一変量の総和を使用する
  • 個別のメソッド
  • Automatic自動的に選択されたメソッド
    "HypergeometricTermFinite"超幾何項の特別な有限和
    "HypergeometricTermGosper"超幾何項の不定和分
    "HypergeometricTermPFQ"超幾何項一般定和分
    "HypergeometricTermZeilberger"超幾何項の定和分
    "LevelCounting"レベル集合における界を数えることに基づいた総和
    "Logarithmic"対数級数総和
    "PeriodicFunction"周期関数総和
    "PolyGammaHypergeometricSeries"ポリガンマ級数表現総和
    "PolyGammaIntegralRepresentation"ポリガンマ積分表現総和
    "PolyGammaSumByParts"部分によるポリガンマ総和
    "Polynomial"多項式総和
    "PolynomialExponential"多項式指数総和
    "PolynomialTrigonometric"多項式三角総和
    "Procedural"手続き的に総和を計算する
    "QHypergeometricTermGosper"q超幾何項の不定和分
    "QHypergeometricTermZeilberger"q超幾何項の定和分
    "QRationalFunction"q有利関数総和
    "RationalExponential"有理数掛ける指数の総和
    "RationalFunction"有理関数総和
    "RationalTrigonometric"有理三角総和
    "TableLookup"表参照に基づいた総和
  • Sumは標準的な本の公式集にあるすべての和を本質的に行うことができる．
  • SumはStandardFormでは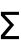を使って出力される．
  • Parallelize[Sum[f,iter]]またはParallelSum[f,iter]はSum[f,iter]をすべてのサブカーネルで並列に計算する． »

例題

すべて開くすべて閉じる

例  (6)

数値的総和：

記号的総和：

sumでを，で下限を入力し，続けてで上限を入力する：

無限和：

不定和分：

j での総和を先に行った多重和：

スコープ  (45)

基本的な用法  (11)

有限範囲における定和分：

刻み幅2を使う：

要素の有限リストを使う：

数列とその部分和（あるいは累積和）をプロットする：

有限範囲における多重和：

異なる刻み幅を使う：

多変量の数列とその部分和をプロットする：

最も外側の総和の限界は内側の変数に依存することができる：

標準的な反復範囲で総和とリストを組み合せる：

反復子のリスト中の要素は任意の式でよい：

無限範囲で総和を求める：

無限範囲での多変量総和：

記号的範囲での総和：

不定和分：

差は加数に等しい：

定和分は不定和分の差として与えられる：

多変量不定和分：

不定和分と定和分の混合：

GenerateConditions を使って答が真となる条件を求める：

Refineで結果の答を簡約する：

Assumptionsを使ってSumに直接仮定を与える：

無限和は収束しないことがある：

Regularizationを使って有限の値を与えることができる無限和もある：

Nを未評価の総和に適用すると，事実上NSumが使われる：

不定和分  (18)

一般関数による式の差分：

多項式は多項式によって総和を求めることができる：

階乗多項式：

指数数列（幾何級数）：

底が2の場合は底が の場合の積分に対する役割と同じ役割を総和に対して果たす：

FibonacciとLucasLは底がGoldenRatioの指数数列である：

指数多項式の総和は指数多項式で求められる：

有理関数の総和は有理関数とPolyGammaで求められる：

有理関数の各差分の総和は有理関数として求められる：

一般に，答にはPolyGammaが含まれる：

すべての有理関数の総和が求められる：

有理指数総和の中には初等関数で求められるものもある：

一般に，答には特殊関数が含まれる：

すべての有理指数関数について，その総和が求められる：

三角多項式の総和は三角関数で求められる：

多項式を掛ける：

指数関数を掛ける：

指数関数と多項式を掛ける：

超幾何項の数列：

DiscreteRatioはすべての超幾何項数列に対して有理である：

多くの関数が超幾何項を与える：

任意の積は超幾何項である：

超幾何項の差分の総和は超幾何項として求められる：

一般に追加的な特殊関数が必要である：

対数総和：

ArcTan総和の中にはArcTanで表せるものがある：

ArcCot総和についても同様である：

指数引数を持つ三角和の中には三角関数で表せるものもある：

PolyGammaおよびその他の式の積：

HarmonicNumberとZetaはPolyGamma数列のような動作をする：

GammaRegularizedの総和：

BetaRegularizedの総和：

q多項式関数：

多重基底q-多項式関数：

混合多重基底q-多項式関数：

q有理関数：

一般に，解を表すのにはQPolyGammaが必要である：

双曲線関数の有理関数はq有理総和に簡約することができる：

q超幾何項：

ホロノミック数列は超幾何項数列を一般化する：

任意のホロノミック数列の総和を求めることができる：

特殊関数の多くがホロノミックである：

周期数列：

総和を求め得る数列を掛け合せた周期数列：

テレスコーピング数列：

定和分  (14)

多項式は多項式の項の和にできる：

指数多項式は指数多項式の項の和にできる：

総和法の条件を求める：

有理関数は常に合計できる：

一般に，RootSum式が必要である：

有理指数関数の和の中には有理指数関数として総和が求められるものがある：

一般に，結果にはLerchPhiが必要である：

無限和の方が簡単なことがよくある：

三角多項式は三角関数の項の和にできる：

多項式を掛ける：

有理関数を掛ける：

指数関数を掛ける：

多項式と有理関数の対数は常に総和が求められる：

無限大の場合は収束解析もある：

収束条件を求める：

超幾何項の総和の中には同じクラスで総和が求められるものがある：

一般に，HypergeometricPFQ関数が必要である：

PolyGammaの積とその他の式：

有理関数および有理指数関数と組み合せる：

他の式を伴ったZetaとHarmonicNumberの積：

これらは一般にオイラー(Euler)総和と呼ばれる：

GammaRegularized総和：

BetaRegularized総和：

ChebyshevU総和：

ChebyshevT総和：

列，行，対角に他の式を掛けたStirlingS1：

StirlingS2で同じことをする：

周期数列に他の式を掛ける：

無限和の方が簡単なことがよくある：

テレスコーピング総和：

多重和  (2)

いくつかの変数を持つ初等関数：

二重超幾何項の総和：

一般化と拡張  (4)

刻み幅2の和：

任意リストの要素の総和：

二重無限和：

ParallelSumはSumを並列に計算する：

Sumは，事実上，ParallelSumを使って自動的に並列化できる：

オプション  (7)

Assumptions  (1)

Assumptionsを使って与えられた対数の不定和分についてより簡単な解を得る：

GenerateConditions  (1)

総和が収束するために必要な条件を生成する：

この有理総和中の加数はパラメータ の値については単数のこともある：

GeneratedParameters  (1)

不定和分について任意定数を生成する：

任意定数のデフォルト値は0である：

Method  (1)

メソッドが異なると結果が異なることがある：

結果は等しくなければならない：

Regularization  (2)

多くの総和は収束しない可能性がある：

Regularizationを使うと多くの総和に解釈が与えられる：

総和が収束するときは常に正規化された値が等しい：

VerifyConvergence  (1)

デフォルトで収束が判定される：

収束判定をしないと発散する総和が答を出すことがある：

アプリケーション  (8)

高等学校の代数  (1)

自然数のベキの総和の式を求める：

よく知られた恒等式を証明する：

有限幾何級数の総和を計算する：

大学の微積分  (1)

無限幾何級数の総和を計算する：

ベキ級数の総和と収束半径を計算する：

パスカルの三角形  (1)

パスカルの三角形の特性を調べる：

パスカルの三角形の任意の行の数の合計は2のベキ乗である：

パスカルの三角形の任意の行の数の交代和は0である：

パスカルの三角形のn番目の行の数の平方の和はBinomial[2n,n]である：

確率と統計  (1)

ポアソン(Poisson)分布の平均と分散は両方ともポアソンパラメータに等しい：

連続的な微積分  (1)

リーマン(Riemann)和の近似を計算する：

Piの近似値  (1)

ラマヌジャン(Ramanujan)の公式を使って π の近似値を計算する：

カタラン数  (1)

CatalanNumberの母関数を求める：

テーラー級数  (1)

関数のテイラー(Taylor)近似を構築する：

特性と関係  (10)

NSumは数値的な方法で総和を計算する：

未評価の総和にNを適用するのは，実質的にNSumを使うことである：

DifferenceDeltaは不定和分の逆の演算子である：

定和分の逆の演算子でもある：

Sumは実質的には特殊な差分方程式をRSolveで解くように解く：

ZTransformを含むいくつかの総和変換が使用できる：

GeneratingFunction：

ExponentialGeneratingFunction：

SumはSumConvergenceを使って無限級数の収束条件を生成する：

Seriesは有限のベキ級数展開を計算する：

SeriesCoefficientは 次のベキ級数係数を計算する：

FourierSeriesは有限フーリエ(Fourier)級数展開を計算する：

Totalはリスト中の項目の総和を求める：

Accumulateはリスト中の部分和を生成する：

考えられる問題  (4)

総和は収束しないことがある：

Regularizationを使うと有限値が与えられるかもしれない：

総和の上限は下限からの整数距離であると考えられる：

GenerateConditionsを使って明示的な仮定を得る：

この例題は，閾値より上で予想外の結果を与える：

これは，第1引数を記号評価することで起る：

手続き型の総和を強制することで，所望の結果を得る：

不正な結果を防ぐために記号評価を避けることもできる：

Sumは，この例に対して予期せぬ結果を与える：

これは，PrimeQを記号評価したためである：

総和は，Primesによって表された場合は未評価で返される：

おもしろい例題  (1)

EllipticTheta関数として表されたガウス(Gauss)の関数のモーメント：

Wolfram Research (1988), Sum, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sum.html （2019年に更新）.

テキスト

Wolfram Research (1988), Sum, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sum.html （2019年に更新）.

CMS

Wolfram Language. 1988. "Sum." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Sum.html.

APA

Wolfram Language. (1988). Sum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sum.html

BibTeX

@misc{reference.wolfram_2024_sum, author="Wolfram Research", title="{Sum}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Sum.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sum, organization={Wolfram Research}, title={Sum}, year={2019}, url={https://reference.wolfram.com/language/ref/Sum.html}, note=[Accessed: 17-November-2024 ]}