



Sum 
更多信息和选项



- Sum[f,{i,imax}] 可被输入为
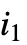 .
. 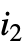 可被输入为
可被输入为 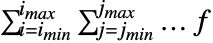 sum
sum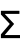 或 \[Sum].
或 \[Sum].- Sum[f,{i,imin,imax}] 可被输入为
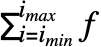 .
. - 在常规输入中,上下限应为
 的底标和顶标,而被嵌入其它文本中时为下标和上标.
的底标和顶标,而被嵌入其它文本中时为下标和上标. - Sum 用标准 Wolfram 语言迭代指定.
- 迭代变量 i 被当作局部变量,相当于使用 Block.
- 如果一个和式的范围是有限的,通常把
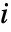 赋给一个由值组成的序列,对每个值计算
赋给一个由值组成的序列,对每个值计算 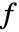 .
. - 在多重求和中,最外层变量的范围首先应被给定. »
- 求和上下限不必是数. 它们可以是 Infinity 或符号表达式. » »
- 如果通过相加有限项,还是不能得出结果,Sum 会尝试给出符号解,在这种情况下,f 首先进行符号运算.
- 定义了不定和
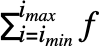 ,以便相对于 i 的差给出 f. »
,以便相对于 i 的差给出 f. » - 定和不定总和可以以任何顺序混合使用. »
- 下列选项可给予:
-
Assumptions $Assumptions 参数的假设 GenerateConditions False 是否产生涉及参数条件的答案 GeneratedParameters None 如何命名产生的参数 Method Automatic 使用的方法 Regularization None 使用什么方案正规化 VerifyConvergence True 是否验证收敛 - Regularization 的可能值包括 None、"Abel"、"Borel"、"Cesaro"、"Dirichlet" 和 "Euler".{reg1,reg2,…} 在多重和中,对不同的变量指定不同的方案.
- Method->"method" 用指定的方法执行求和.
- Method->{"strategy",Method->{"meth1","meth2",…}} 使用方法 "methi",用指定的策略方法控制.
- 可能的策略方法包括:
-
"SequentialFirstToSucceed" 按顺序尝试每种方法,直到某一种成功 "SequentialBestQuality" 按顺序尝试每种方法,返回最好结果 "ParallelFirstToSucceed" 同时尝试每种方法,直到某一种成功 "ParallelBestQuality" 同时尝试每种方法,返回最好结果 "IteratedSummation" 使用迭代变量求和 - 指定的方法包括:
-
Automatic 自动选择的方法 "HypergeometricTermFinite" 特别有限超几何项求和 "HypergeometricTermGosper" 无限超几何项求和 "HypergeometricTermPFQ" 一般明确超几何项求和 "HypergeometricTermZeilberger" 明确超几何项求和 "LevelCounting" 基于水平集计数方案的求和 "Logarithmic" 对数系列求和 "PeriodicFunction" 周期函数求和 "PolyGammaHypergeometricSeries" 多伽玛级数表示法求和 "PolyGammaIntegralRepresentation" 多伽玛积分表示法求和 "PolyGammaSumByParts" 多伽玛部分求和 "Polynomial" 多项式求和 "PolynomialExponential" 多项式指数总和 "PolynomialTrigonometric" 多项式三角求和 "Procedural" 程序地计算总和 "QHypergeometricTermGosper" 无限 q 超几何项求和 "QHypergeometricTermZeilberger" 明确 q 超几何项求和 "QRationalFunction" q 有理函数求和 "RationalExponential" 有理指数总和 "RationalFunction" 有理函数求和 "RationalTrigonometric" 有理三角求和 "TableLookup" 基于查表求和 - Sum 可完成标准参考手册中给出的所有求和.
- Sum 在 StandardForm 中使用
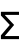 输出.
输出. - Parallelize[Sum[f,iter]] 或 ParallelSum[f,iter] 在所有子内核上并行计算 Sum[f,iter]. »
范例
打开所有单元 关闭所有单元范围 (45)
基本用途 (11)
使用 GenerateConditions 获得答案是正确的的条件:
Refine 或简化导致的答案:
使用 Assumptions 直接提供对 Sum 的假设:
使用 Regularization 给某些不定和分配一个有限值:
不定和 (18)
Fibonacci 和 LucasL 是基于 GoldenRatio 的指数序列:
有理函数可以用有理函数和 PolyGamma 来求和:
一般来说,答案涉及到 PolyGamma:
对所有超几何项序列, DiscreteRatio 是有理数:
对 ArcCot 的总和也一样:
PolyGamma 和其他表达式的乘积:
HarmonicNumber 和 Zeta 有和 PolyGamma 序列类似的表现:
一般情况下,需要 QPolyGamma 来表达答案:
确定和 (14)
一般情况下,需要 RootSum 表达式:
一般情况下,结果需要 LerchPhi:
一般情况下,需要 HypergeometricPFQ 函数:
PolyGamma 和其他表达式的乘积:
Zeta 和 HarmonicNumber 与其他表达式的乘积:
ChebyshevU 和:
ChebyshevT 和:
StirlingS1 和列,行,对角线一起乘以其他表达式:
StirlingS2 也同样:
推广和延伸 (4)
选项 (7)
Assumptions (1)
使用 Assumptions 对不定对数总和获得一个更简单的答案:
Regularization (2)
应用 (8)
帕斯卡尔三角形 (1)
Catalan 数 (1)
找到 CatalanNumber 的生成函数:
属性和关系 (10)
NSum 用数值方法计算和:
DifferenceDelta 是不定求和的逆操作:
Sum 实际上求解一个特殊的微分方程,类似用 RSolve:
可用几种求和变换包括 ZTransform:
ExponentialGeneratingFunction:
Sum 使用 SumConvergence 创造无穷级数收敛的条件:
Series 计算有限幂级数的展开:
SeriesCoefficient 计算第 ![]() 个幂级数系数:
个幂级数系数:
FourierSeries 计算有限傅立叶级数展开:
Total 对一个列表中的元素求和:
Accumulate 产生一个列表的部分和:
可能存在的问题 (4)
使用 Regularization 可能给出一个有限值:
使用 GenerateConditions 得到明确的假设:
Sum 给出对这个范例的预期外的结果:
这是由于对 PrimeQ 的符号化估计的结果:
当总和被以 Primes 形式表达时,返回未估计的和:
巧妙范例 (1)
高斯函数的阶距表示为 EllipticTheta 函数:
技术笔记
-
▪
- 符号运算 ▪
- 求和与求积 ▪
- 级数的和 ▪
- 关于内部实现的一些注释: 代数和微积分
历史
1988年引入 (1.0) | 在以下年份被更新:1996 (3.0) ▪ 2008 (7.0) ▪ 2019 (12.0)
文本
Wolfram Research (1988),Sum,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Sum.html (更新于 2019 年).
CMS
Wolfram 语言. 1988. "Sum." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/Sum.html.
APA
Wolfram 语言. (1988). Sum. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Sum.html 年
BibTeX
@misc{reference.wolfram_2025_sum, author="Wolfram Research", title="{Sum}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Sum.html}", note=[Accessed: 02-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_sum, organization={Wolfram Research}, title={Sum}, year={2019}, url={https://reference.wolfram.com/language/ref/Sum.html}, note=[Accessed: 02-February-2026]}