Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram 语言与系统参考资料中心

FourierTransform

FourierTransform

FourierTransform[expr,t,ω]

给出 expr 的符号傅立叶变换.

FourierTransform[expr,{t₁,t₂,…},{ω₁,ω₂,…}]

给出 expr 的多维傅立叶变换.

更多信息和选项

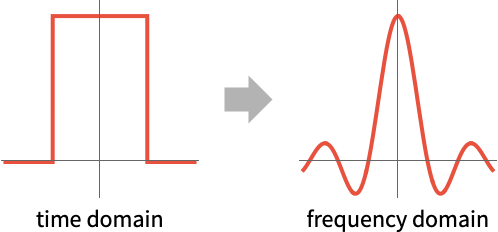
傅立叶变换及其逆变换是一种在时域和频域之间转换的方式.
傅立叶变换通常用于将常微分方程和偏微分方程分别简化为代数方程或常微分方程. 它们还广泛应用于控制理论和信号处理领域. 此外，它们在研究量子力学现象、噪声过滤等方面也有应用.
时域函数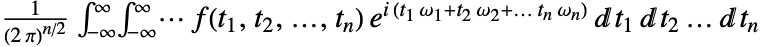的傅立叶变换是频域函数：

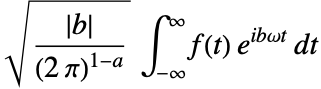在缺省情况下，函数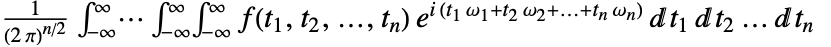的傅立叶变换的定义为 .
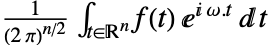函数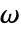的多维傅立叶变换默认定义为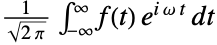或向量表示形式 .
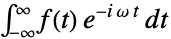不同的定义选择可以使用选项 FourierParameters 指定.
如果第三个参数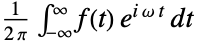被赋予数值，则积分会通过数值方法计算.
渐近傅立叶变换可以通过 Asymptotic 方法计算.
以下是几种相关的傅立叶变换：

	FourierTransform	无限连续时间函数 (FT)
	FourierSequenceTransform	无限离散时间函数 (DTFT)
	FourierCoefficient	有限连续时间函数 (FS)
	Fourier	有限离散时间函数 (DFT)

傅立叶变换是函数在施瓦茨向量空间上的一个自同构，其导数快速降低，因此在其对偶空间（缓和分布空间）中也诱导出一个自同构. 这些空间包括绝对可积函数、多项式增长的良好函数以及紧支撑分布.
因此，FourierTransform 不仅可以处理绝对可积函数，还可以处理诸如 DiracDelta 函数等各种缓增分布，从而扩大了它可以有效变换的函数或广义函数的范围.
可以给出下列选项：

	AccuracyGoal	Automatic	绝对精度的目标位数
	Assumptions	$Assumptions	所做的参数假定
	FourierParameters	{0,1}	定义傅立叶变换的参数
	GenerateConditions	False	是否生成涉及参数条件的答案
	PerformanceGoal	$PerformanceGoal	优化的性能方面
	PrecisionGoal	Automatic	精度的目标位数
	WorkingPrecision	Automatic	内部计算使用的精度

常见的 FourierParameters 设置包括：
{0,1} 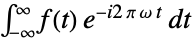默认设置/物理学

{1,-1} 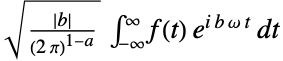系统工程/数学

{-1,1} 经典物理学

{0,-2Pi} 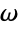普通频率

{a,b} 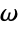通用设置
在 TraditionalForm 中，FourierTransform 用 ℱ 输出. »

范例

打开所有单元关闭所有单元

基本范例 (6)

计算函数的傅立叶变换：

绘制函数及其傅立叶变换：

的傅立叶变换：

按照系统工程惯例，更改参数：

高斯函数的傅立叶变换是另一个高斯函数：

绘制两个高斯函数：

计算多元函数的傅立叶变换：

绘制结果：

计算单点的变换：

范围 (44)

基本用法 (4)

对于符号参数，函数的傅立叶变换：

三角函数的傅立叶变换：

对参数 ω 的数值，计算其傅立叶变换：

TraditionalForm 格式：

初等函数 (8)

幂函数的傅立叶变换：

多项式：

有理函数的傅立叶变换：

绘制该变换：

绘制实部和虚部：

平方根的倒数：

绘制该变换：

涉及三角函数的表达式：

正弦函数与线性函数的比率：

绘制该变换：

初等函数的复合：

绘制该变换：

对数函数：

绘制该变换：

特殊函数 (5)

Sinc 函数：

绘制该变换：

涉及贝塞尔函数的表达式：

绘制该变换：

SinIntegral 函数：

拉盖尔多项式：

艾里函数：

绘制复数的傅立叶变换幅值：

分段函数和分布 (7)

分段函数的傅立叶变换：

使用 Sign 函数求绝对值：

将正弦函数限制为半周期：

三角函数：

UnitStep 函数与余弦函数的乘积：

绘制幅值和相位：

周期函数 (5)

SquareWave 的傅立叶变换：

TriangleWave：

SawtoothWave：

周期为的全波整流函数：

整流波：

广义函数 (5)

涉及 HeavisideTheta 的傅立叶变换：

绘制幅值和相位：

DiracDelta 的导数：

HeavisideLambda：

多元函数 (5)

常数的双变量傅立叶变换：

指数函数：

三变量余弦：

幂与指数的乘积：

指数函数与 SquareWave 函数乘积的傅立叶变换：

形式性质 (3)

一阶导数的傅立叶变换：

二阶导数的傅立叶变换：

傅立叶变换贯穿于方程之中：

数值运算 (2)

计算单个点的傅立叶变换：

或者，以符号方式计算傅立叶变换：

然后对的具体值进行求值：

选项 (7)

AccuracyGoal (1)

选项 AccuracyGoal 设置精度的位数：

使用默认设置：

Assumptions (1)

使用 Assumptions 指定变量的范围：

FourierParameters (2)

具有不同参数的单位框函数的傅立叶变换：

设置特定的全局参数选择，以使用普通频率每次会话工作一次：

恢复默认设置：

GenerateConditions (1)

使用 GenerateConditionsTrue 获取结果有效时的参数条件：

PrecisionGoal (1)

选项 PrecisionGoal 设置积分的相对误差：

使用默认设置：

WorkingPrecision (1)

如果指定了 WorkingPrecision，则计算按该工作精度进行：

使用默认设置：

应用 (11)

信号与系统 (3)

求信号的卷积：

傅立叶变换的乘积：

求逆变换：

与 Convolve 比较：

两个信号乘积的频谱，其中一个信号在频域中给出：

信号的傅立叶变换：

与原始信号乘积的傅立叶变换是其变换的卷积：

其频谱：

由常微分方程定义的 LTI 系统的频率响应：

对方程应用傅立叶变换：

求解的傅立叶变换：

LTI 系统的频率响应是输出函数与输入函数的傅立叶变换之比：

常微分方程 (1)

使用傅立叶变换求解微分方程：

对方程应用傅立叶变换：

求解傅立叶变换：

求逆变换来获得解：

与 DSolveValue 比较：

偏微分方程 (1)

考虑热方程：，初始条件为：

关于的傅立叶变换：

使用和，求解此常微分方程：

计算逆傅立叶变换：

并进行卷积得到解：

考虑初始条件和的特殊情况：

与 DSolveValue 比较：

绘制不同值的初始条件和解：

在 - 平面上绘制解：

积分计算 (1)

计算以下定积分：

计算关于的傅立叶变换并交换变换和积分的顺序：

在上积分：

利用逆傅立叶变换得到结果：

与 Integrate 比较：

其它应用 (5)

阻尼正弦曲线的幂频谱：

平面中径向对称函数的傅立叶变换可以表示为汉克尔变换. 验证由下面定义的函数的这种关系：

绘制函数：

计算它的傅立叶变换：

用 HankelTransform 得到同样的结果：

绘制傅立叶变换：

生成一组径向对称函数的傅立叶变换图集：

计算这些函数的汉克尔变换：

生成要求的傅立叶变换图集：

计算平稳 OrnsteinUhlenbeckProcess 的功率谱：

快速浏览一下海森堡测不准原理：

考虑一个固定面积的盒框函数作为粒子的位置空间波函数. 它的傅立叶变换给出粒子的动量空间波函数：

当较小时，固定面积盒框的高度较大，粒子的位置几乎可以确定. 动量空间波函数在其两个最接近零的根之间的值约为，这使得几乎无法确定其动量. 同样地，反之亦然，如下所示：

属性和关系 (6)

默认情况下，的傅立叶变换为：

对于，定积分变成：

与 FourierTransform 比较：

用 Asymptotic 计算渐近逼近：

FourierTransform 和 InverseFourierTransform 是互逆的：

对奇函数，FourierTransform 和 FourierCosTransform 是相等的：

对偶函数，FourierTransform 和 FourierSinTransform 的差异为 ：

可能存在的问题 (1)

一个逆傅立叶变换的结果可能和初始不相同：

巧妙范例 (2)

加权的 Hermite 多项式的傅立叶变换有非常简单的形式：

创建一个基本傅立叶变换的表格：

Top