GeometricScene
GeometricScene[{p1,p2,…},{hyp1,hyp2,…}]
表示由用符号点 pi 给出的假设 hypi 定义的抽象二维几何场景.
GeometricScene[{{p1,p2,…},{k1,k2,…}},hyps]
表示一个场景,其假设取决于符号标量 ki.
GeometricScene[{{p1{x1,y1},…},{k1v1,…}},hyps]
表示一个特定实例,其中所有点和标量都有明确的值.
GeometricScene[…,…,{con1,con2,…}]
表示一个场景以及与场景相关的一些结论 coni.
GeometricScene[{{{p1{x1,y1},…},{k1v1,…}},…},hyps]
表示一组同一场景的特定实例.
GeometricScene[{scene1,scene2,…}]
将几个场景实例组合为一个场景对象.
更多信息和选项




- 所有点都有明确的坐标,所有标量都有明确的值的 GeometricScene 对象,通常显示为交互式图表.
- 在 GeometricScene[{p1,p2,…},…] 中,pi 可以是字符串、符号或其他符号表达式.
- RandomInstance 给出能满足给定假设的 pi 和 ki 的特定值.
- 场景中的假设可以列出必须出现在场景中的对象,并且可以给出关于这些对象的关系和其他论断.
- 可用以下基元表示几何对象:
-
Circle[pt,r] 圆 Disk[pt,r] 实心圆盘 HalfLine[{pt1,pt2}] 半直线或射线 InfiniteLine[{pt1,pt2}] 无限长直线 Line[{pt1,…}] 直线 Parallelogram[pt,{v1,v2}] 平行四边形 Point[pt] 点集 Polygon[{pt1,…}] 简单多边形 Rectangle[pt1,pt2] 长方形 RegularPolygon[n] 正多边形 Triangle[{pt1,…}] 三角形 - 几何对象中的点和标量可以是符号,也可以有明确的值.
- 可用下面的元素表示应用于几何对象的构建:
-
AngleBisector[{pt1,pt2,pt3}] 无限长直线形式的角平分线 CircleThrough[{pt1,…}] 穿过点的圆 CircularArcThrough[{pt1,…}] 穿过点的圆弧 Circumsphere[{pt1,pt2,pt3}] 外接球 Insphere[{pt1,pt2,pt3}] 内切球 InfiniteLineThrough[{pt1,…}] 穿过无序点的无限长直线 Midpoint[{pt1,pt2}] 中点 PerpendicularBisector[{pt1,pt2}] 无限长直线形式的垂直平分线 RegionBoundary[reg] 边界 RegionCentroid[reg] 以点的形式给出区域的几何中心 RegionNearest[reg, pt] 区域中最近的点 TriangleCenter[tri,type] 三角形的指定类型的心 TriangleConstruct[tri,type] 三角形的指定类型的构建 - 可使用以下关于几何对象的论断和它们的属性:
-
pt∈reg, RegionMember[reg,pt] 点位于区域中 x… 值或对象的相等性 x>…, x<…, … 值与值的不相等性 GeometricAssertion[objs,prop] 已命名的关于几何对象的论断 GeometricStep[{hyp1,hyp2,…}] 由多个假设组成的步骤 - 可使用以下几何对象的测量:
-
ArcLength[reg] 弧长 Area[reg] 面积 EuclideanDistance[pt1,pt2] 欧氏距离 Perimeter[reg] 周长 PlanarAngle[{pt1,pt2,pt3}] 角度 PolygonAngle[poly,pt] 多边形的角 RegionDistance[reg,pt] 到区域的距离 RegionMeasure[reg] 区域的度量 SignedRegionDistance[reg,pt] 有符号的到区域的距离 TriangleMeasurement[tri,type] 三角形的度量 - GeometricScene[…]["prop"] 给出几何场景的属性 prop. 可能的属性包括:
-
"AlgebraicFormulation" 给出针对点和量的约束条件的代数表达式 "Conclusions" 结论列表 "Graphics" 场景图,以 Graphics 对象的形式给出 "GraphicsList" 有多个步骤和/或实例的场景的 Graphics 列表 "Hypotheses" 假设列表 "Instances" 场景实例列表 "Parameters" 场景的点和标量值指定列表 "Points" 场景中点的规范的列表 "Properties" 所有支持的属性的列表 "Quantities" 场景中标量值的规范的列表 - 对于明确的场景实例 scenei,GeometricScene[{scene1,scene2,…}] 被转换为 GeometricScene 对象,其中给定多个点和标量值列表,只要所有的 scenei 都是同一抽象场景的实例.
- 当 GeometricScene 表示一个抽象场景的多个实例时,通常将其显示为 MenuView 对象,每个菜单项显示一个实例.
- 可用 Style 指定几何对象的样式. 样式规范不影响场景的几何意义.
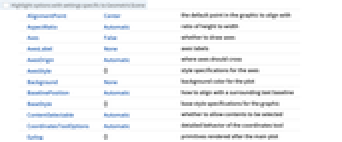
- GeometricScene 接受 Graphics 选项,并增加以下内容: [所有选项的列表]
-
UnconstrainedParameters None 没有约束的参数的列表 GeometricStylingRules Automatic 几何场景中的基元样式 PlotTheme $PlotTheme 场景整体样式 - FindGeometricConjectures 之类的函数会给出 GeometricScene 对象的结论.
- GeometricSolveValues 等函数可求解 GeometricScene 对象中的符号几何量. »
所有选项的列表


范例
打开所有单元关闭所有单元基本范例 (4)
表示一个符号几何场景,其中含有由点 a、b、c 和一个 30° 的角组成的三角形:
RandomInstance 给出点的明确坐标:
考虑这样一个场景:一个直角三角形的边长已确定,但斜边 ![]() 未知:
未知:
使用 GeometricSolveValues 求出斜边 ![]() :
:
范围 (4)
将场景组合为一个 GeometricScene 对象:
使用 GeometricAssertion 表示描绘线-圆相切的场景:
从 GeometricScene 对象提取结论:
使用 GeometricStep 来表示通过点 a、b、c 构成的角的角平分线的构造:
可使用 Style 设计几何场景中各个对象的样式:
选项 (6)
应用 (7)
属性和关系 (2)
通过子值 "AlgebraicFormulation" 可以提取 GeometricScene 的成立条件:
GeometricTest 直接给出这些条件:
这些条件与 GeometricScene 子值 "AlgebraicFormulation" 返回的条件相同:
文本
Wolfram Research (2019),GeometricScene,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GeometricScene.html (更新于 2024 年).
CMS
Wolfram 语言. 2019. "GeometricScene." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/GeometricScene.html.
APA
Wolfram 语言. (2019). GeometricScene. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GeometricScene.html 年