StreamDensityPlot[{{vx,vy},r},{x,xmin,xmax},{y,ymin,ymax}]
ベクトル場{vx,vy}の流線プロットをスカラー場 r の背景濃度のプロットに重ね合された x と y の関数として生成する.
StreamDensityPlot[{vx,vy},{x,xmin,xmax},{y,ymin,ymax}]
スカラー場がベクトル場のノルムであるとする.
StreamDensityPlot[{{vx,vy},{wx,wy},…,r},{x,xmin,xmax},{y,ymin,ymax}]
複数のベクトル場のプロットを生成する.
StreamDensityPlot[…,{x,y}∈reg]
変数{x,y}が,幾何学領域 reg にあるものと解釈する.




StreamDensityPlot
StreamDensityPlot[{{vx,vy},r},{x,xmin,xmax},{y,ymin,ymax}]
ベクトル場{vx,vy}の流線プロットをスカラー場 r の背景濃度のプロットに重ね合された x と y の関数として生成する.
StreamDensityPlot[{vx,vy},{x,xmin,xmax},{y,ymin,ymax}]
スカラー場がベクトル場のノルムであるとする.
StreamDensityPlot[{{vx,vy},{wx,wy},…,r},{x,xmin,xmax},{y,ymin,ymax}]
複数のベクトル場のプロットを生成する.
StreamDensityPlot[…,{x,y}∈reg]
変数{x,y}が,幾何学領域 reg にあるものと解釈する.
詳細とオプション



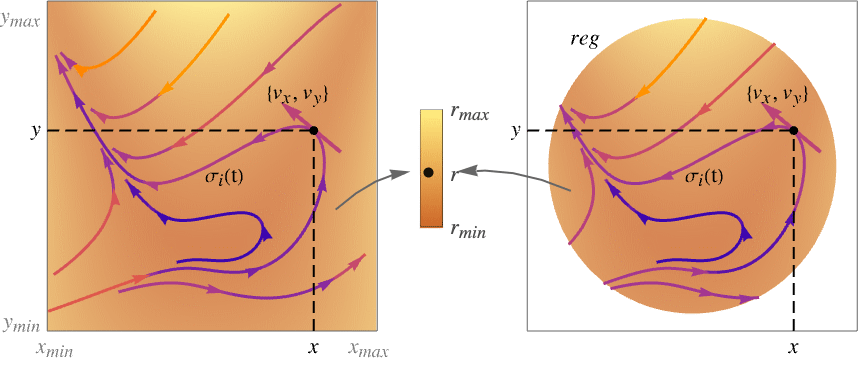
- StreamDensityPlotはすべての点におけるベクトル場の局所的方向を示す流線をプロットする.
- StreamDensityPlotは,スカラー場 r の密度プロットを背景とし,そこに重ね合せてベクトル場{vx,vy}の流線プロットを生成する.
- StreamDensityPlotは,
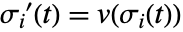 と
と 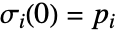 で定義された流線
で定義された流線 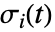 をプロットする.
をプロットする.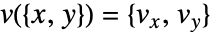 はベクトルデータの補間関数で,
はベクトルデータの補間関数で,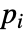 は初期流点である.流線
は初期流点である.流線 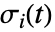 は点
は点 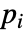 を通る曲線で,その接戦は各点におけるベクトル場
を通る曲線で,その接戦は各点におけるベクトル場 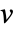 に対応する.
に対応する. - 流線はスカラー場
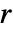 の密度プロットの上に描画される.その初期値はベクトル場
の密度プロットの上に描画される.その初期値はベクトル場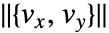 の強度である.
の強度である. - 流線はベクトル場
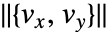 の強度
の強度 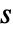 に従って彩色される.矢印は
に従って彩色される.矢印は 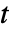 が大きくなる方向を向く.
が大きくなる方向を向く. - StreamDensityPlotはデフォルトで,プロット全体を通してほぼ一様な密度に達するのに十分な流線を示す.
- StreamDensityPlotは vi等を評価しても実数にならない位置では流線を示さない.
- StreamDensityPlotは,実質的にBlockを使い変数 x と y を局所的なものとして扱う.
- StreamDensityPlotには属性HoldAllがあり,x と y に特定の数値を割り当てた後ではじめて vi等を評価する.
- 場合によっては x と y に特定の数値を割り当てる前にEvaluateを使って vi等を記号的に評価する方がより効率がよいかもしれない.
- StreamDensityPlotにはGraphicsと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
- MeshFunctions,RegionFunction,ColorFunction,StreamColorFunction中の関数に渡される引数は x, y, vx, vy, r である.
- デフォルト設定のMeshFunctions->{#5&}では,スカラー場 r にメッシュラインが描かれる.
- 次は,ScalingFunctionsの可能な設定である.
-
{sx,sy} x 軸と y 軸をスケールする - 次は,よく使われる組込みのスケーリング関数 s である.
-
"Log" 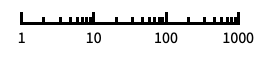
自動目盛ラベル付きの対数スケール "Log10" 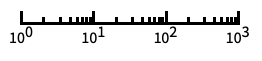
10のベキ乗に目盛が付いた,10を底とする対数スケール "SignedLog" 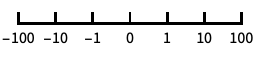
0と負の数を含む対数に似たスケール "Reverse" 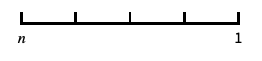
座標の向きを逆にする "Infinite" 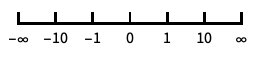
無限スケール
全オプションのリスト



例題
すべて開く すべて閉じる例 (4)
スコープ (24)
サンプリング (11)
2つのベクトル場の流線を,最初のベクトル場の強度に基づいた背景色でプロットする:
Evaluateを使って,数値割当ての前にベクトル場を記号的に評価する:
明示的にシードされた流線のスタイルに自動的なシードと明示的なシードの両方を使う:
領域はMeshRegionで指定することができる:
プレゼンテーション (13)
StreamScaleの設定で異なる破線と鏃を指定する:
オプション (85)
ColorFunction (6)
ColorFunctionScaling (4)
ColorFunctionScaling->Falseを使ってスケールされていない値を得る:
Mesh (5)
PlotRange (7)
StreamColorFunction (6)
ColorDataから任意の名前付き色階調度を使う:
定義済みの色階調度にColorDataを使う:
StreamColorFunctionScaling->Falseを使ってスケールされていない値を得る:
StreamColorFunctionScaling (4)
StreamColorFunctionScaling->Falseを使ってスケールされていない値を得る:
StreamMarkers (7)
StreamPoints (6)
StreamScale (9)
StreamStyle (5)
StreamStyleでは,StreamColorFunctionは色より優先順位が高い:
StreamColorFunctionNoneと設定してStreamStyleで色を指定する:
アプリケーション (16)
2Dハミルトン(Hamilton)系のハミルトン方程式に重ね合わされた流線を示す:
NDSolveがいかに不変量を保存するかを検証する:
流線プロットをインタラクティブな微分方程式のデモの背景として使う:
Manipulateを使ってパラメータ化されたベクトル場を調べる:
アニメーションのためにラスタライズしたプロットのリストを生成する:
もとのベクトルグラフィックスの代りにラスタのリストをアニメーションにした方が,メモリが少なくて済むかもしれない:
流線の色をベクトルのノルムの方向にシフトするアニメーションを作成する:
いくつかの例題でさまざまな流線のスタイルとスケールを調べてみる:



特性と関係 (12)
データのプロットにListStreamDensityPlotを使う:
StreamPlotを使ってスカラー場のプロットなしで流線だけをプロットする:
VectorDensityPlotを使って流線の代りにベクトルで関数をプロットする:
ListVectorDensityPlotを使って流線の代りにベクトルでデータをプロットする:
VectorPlotを使ってスカラー場のプロットなしで流線の代りにベクトルでプロットする:
VectorPlot3Dを使って3Dベクトル場を可視化する:
SliceVectorPlot3Dを使って曲面上に3Dベクトル場を可視化する:
StreamDensityPlotは必要であればより多くの点をサンプルとして使う:
スカラー場はDensityPlotを使ってそれ自身でプロットすることができる:
LineIntegralConvolutionPlotを使ってベクトル場の線形積分たたみ込みをプロットする:
GeoStreamPlotは地球の地図上に流線をプロットする:
特性と関係 (12)
VectorDensityPlotを使って流線ではなくベクトルでプロットする:
StreamPlotまたはVectorPlotをスカラー場の密度プロットなしで関数をプロットするのに使う:
ListStreamDensityPlotを使ってデータをプロットする:
ListStreamPlotを密度プロットなしのデータのプロットに使う:
ListVectorPlotを使って流線の代りにベクトルをプロットする:
ListVectorDensityPlotを使ってベクトルに密度プロットを加える:
VectorDisplacementPlotを使って変位ベクトル場に関連付けられた領域の変形を可視化する:
ListVectorDisplacementPlotを使って同じ変形をデータに基づいて可視化する:
VectorDisplacementPlot3Dを使って変位ベクトル場に関連付けられた3D領域の変形を可視化する:
ListVectorDisplacementPlot3Dを使って同じ変形をデータに基づいて可視化する:
VectorPlot3DまたはStreamPlot3Dを使って3Dベクトル場を可視化する:
ListVectorPlot3DまたはListStreamPlot3Dを使って同じ3Dベクトル場をデータに基づいて可視化する:
SliceVectorPlot3Dを使って曲面上に3Dベクトル場データを曲面に沿って可視化する:
ListSliceVectorPlot3Dを使って同じ3Dベクトル場データをデータに基づいて可視化する:
StreamDensityPlotは必要であればより多くの点をサンプルとして使う:
スカラー場はListDensityPlotを使ってそれ自身でプロットすることができる:
ListLineIntegralConvolutionPlotを使ってベクトル場データの線積分のたたみ込みをプロットする:
ComplexVectorPlotまたはComplexStreamPlotを使って複素変数の複素関数をベクトル場としてまたは流線でプロットする:
GeoVectorPlotで地図上にベクトルをプロットする:
GeoStreamPlotでベクトルの代りに流線をプロットする:
関連するガイド
-
▪
- ベクトルの可視化
履歴
2008 で導入 (7.0) | 2012 で更新 (9.0) ▪ 2014 (10.0) ▪ 2018 (11.3) ▪ 2020 (12.2) ▪ 2022 (13.1)
テキスト
Wolfram Research (2008), StreamDensityPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/StreamDensityPlot.html (2022年に更新).
CMS
Wolfram Language. 2008. "StreamDensityPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/StreamDensityPlot.html.
APA
Wolfram Language. (2008). StreamDensityPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StreamDensityPlot.html
BibTeX
@misc{reference.wolfram_2025_streamdensityplot, author="Wolfram Research", title="{StreamDensityPlot}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/StreamDensityPlot.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_streamdensityplot, organization={Wolfram Research}, title={StreamDensityPlot}, year={2022}, url={https://reference.wolfram.com/language/ref/StreamDensityPlot.html}, note=[Accessed: 06-February-2026]}