Variance
更多信息




- Variance 衡量数据或分布的分散度.
- Variance[data] 给出方差的无偏估计.
- 对于 VectorQ data
 ,方差估计值
,方差估计值 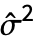 由
由 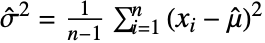 给出(对于实数),对于复数,由
给出(对于实数),对于复数,由 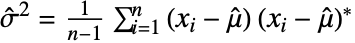 给出,
给出,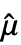 =Mean[data].
=Mean[data]. - 对于 MatrixQ data,针对每个列向量计算方差估计值
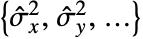 , Variance[{{x1,y1,…},{x2,y2,…},…}] 等价于 {Variance[{x1,x2,…}],Variance[{y1,y2,…}]}. »
, Variance[{{x1,y1,…},{x2,y2,…},…}] 等价于 {Variance[{x1,x2,…}],Variance[{y1,y2,…}]}. » - 对于 ArrayQ data,方差等价于 ArrayReduce[Variance,data,1]. »
- 对于由实数组成的加权 WeightedData[{x1,x2,…},{w1,w2,…}],由
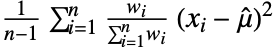 给出方差. »
给出方差. » - Variance 可处理数值和符号 data.
- data 可以有以下其他形式和解释:
-
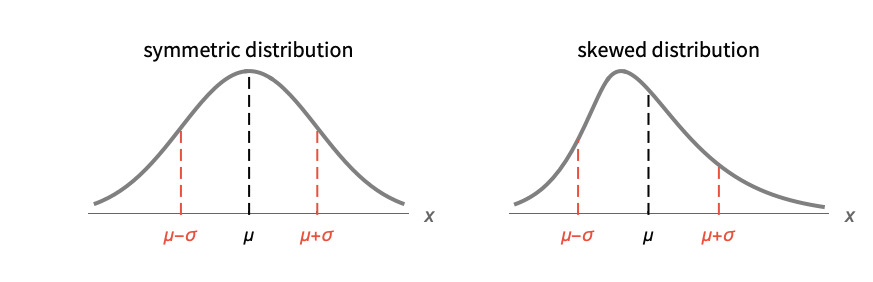
Association 数值(键被忽略) » SparseArray 数组,相当于 Normal[data] » QuantityArray 量组成的数组 » WeightedData 加权方差,基于 EmpiricalDistribution » EventData 基于 SurvivalDistribution » TimeSeries, TemporalData, … 向量或数值组成的数组(忽略时间戳) » Image,Image3D RGB 通道的值或灰度的强度值 » Audio 所有通道的幅值 » DateObject, TimeObject list of dates or list of time » - 对于单变量分布 dist,由 σ2=Expectation[(x-μ)2,xdist] 给出方差,其中 μ=Mean[dist]. »
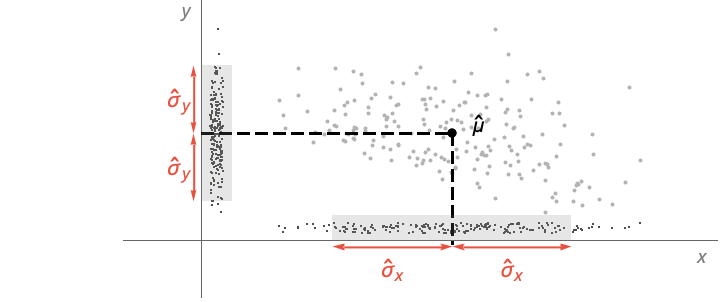
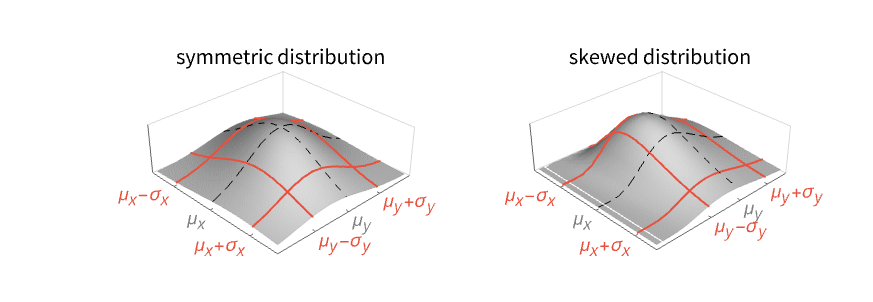
- 对于多变量分布 dist,方差由 {σx2,σy2,…}=Expectation[{(x-μx)2,(y-μy)2,…},{x,y,…}dist] 给出. »
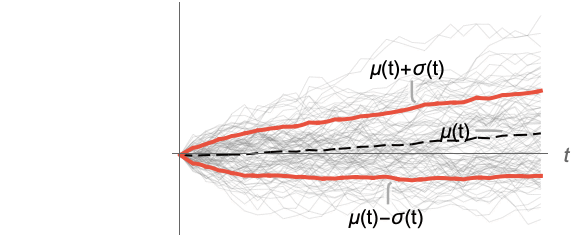
- 对于随机过程 proc,可计算时间 t 处切片分布 SliceDistribution[proc,t] 的方差函数,即 σ[t]2=Variance[SliceDistribution[proc,t]]. »
范例
打开所有单元关闭所有单元范围 (22)
基本用法 (7)
数组数据 (5)
矩阵的 Variance 给出列的方差:
张量的 Variance 给出第一级的列的方差:
当输入为 Association 时,Variance 只作用于值:
可以像使用密集数组一样使用 SparseArray 数据:
求 QuantityArray 的方差:
图像和音频数据 (2)
应用 (5)
Variance 是分散度的测量:
属性和关系 (11)
Variance 的平方根是 StandardDeviation:
Variance 是来自于 Mean 值偏差的某种程度的 Norm 平方:
Variance 是某种程度的 CentralMoment:
Variance 的平方根是偏差的某种程度的 RootMeanSquare:
Variance 是来自于 Mean 值的平方偏差的某种程度的 Mean:
Variance 是来自于 Mean 值的某种程度的 SquaredEuclideanDistance:
如果所有数据的绝对偏差小于1 ,则 Variance 的值小于 MeanDeviation :
如果所有数据的绝对偏差大于1,则 Variance 的值大于 MeanDeviation :
随机变量的 Variance ,可以视为一个 Expectation:
Variance 给出无偏样本估计:
无偏意味着关于人口分布的样本方差的期望值等于基本分布的方差:
Variance 给出无偏加权的样本估计:
巧妙范例 (1)
对于 20、100 和 300 个样本的 Variance 估计量的分布:
文本
Wolfram Research (2003),Variance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Variance.html (更新于 2024 年).
CMS
Wolfram 语言. 2003. "Variance." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Variance.html.
APA
Wolfram 语言. (2003). Variance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Variance.html 年