BinomialDistribution
BinomialDistribution[n,p]
n 回の試行での成功確率が p である二項分布を表す.
詳細
- 二項分布における値
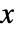 の確率は,0から n までの整数について
の確率は,0から n までの整数について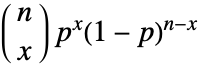 である. »
である. » - BinomialDistributionでは,n は任意の非負の整数でよい.
- BinomialDistributionでは,n と p は無次元量でよい. »
- BinomialDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- BinomialDistribution[n,p]は,整数値
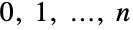 のところで定義され,非負の実数 p (
のところで定義され,非負の実数 p (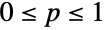 )でパラメータ化された離散統計分布を表す.二項分布は,単峰性で峰が
)でパラメータ化された離散統計分布を表す.二項分布は,単峰性で峰が 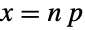 の平均にある,離散確率密度関数(PDF)を持つ.母数 n および p は,PDFの,高さ,水平位置,および歪みを決定する.
の平均にある,離散確率密度関数(PDF)を持つ.母数 n および p は,PDFの,高さ,水平位置,および歪みを決定する. - 二項分布の研究は,18世紀初頭のヤコブ・ベルヌーイの業績まで遡ることができ,研究対象となる最古の分布の一つとなっている.二項分布は,(公正あるいは不正な)n 個のコイントスの行為をモデル化のために設計された.トスするコインは,独立で等しく,独立的に順次置換えたものでサンプルを取られる.伝統的に,p は実験が「成功する」確率であり,
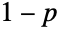 は「失敗する」確率であると考えられる.コイントスの例では,
は「失敗する」確率であると考えられる.コイントスの例では,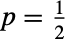 は公正なコインのトスに相当する.
は公正なコインのトスに相当する. - 非常に単純に定義されているにもかかわらず,二項分布は,より複雑な多くの数学概念の基礎になっている.例えば,二項分布は,成功確率が p の有限の n 段階ベルヌーイ過程(つまり,それぞれがBernoulliDistribution[p]によって独立どう分布に従っている,有限な一連の確率変数からなる離散時間確率過程)から生じた成功の分布として考えることができる.同様に,二項分布は,二項過程(BinomialProcess)のスライス分布(SliceDistribution)である.この二項過程は,二項分布に従う独立同分布の確率変数の有限列からなる離散時間・離散状態の確率過程であり,確率変数間の時間は幾何分布 (GeometricDistribution)に従う.確率変数の有限列からなる)離散時間・離散状態の確率過程,さらに,例えば n 個の(公正または不正な)サイコロを振って特定の値が出る確率等,多くの現実世界の事象が二項過程としてモデル化できる.移民パターンやある種の待ち行列モデル等で二項分布間の驚くべき関係も発見されている.
- RandomVariateを使って,二項分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BinomialDistribution[n,p]](より簡略すると xBinomialDistribution[n,p])を使って,確率変数 x が,二項分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BinomialDistribution[n,p],x]およびCDF[BinomialDistribution[n,p],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合が二項分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから二項パラメトリック分布を推定することが,FindDistributionParametersを使ってデータを二項分布にフィットすることができる.ProbabilityPlotを使って記号的な二項分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号的な二項分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された二項分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って二項分布を含む高次元分布を構築することが,ProductDistributionを使って二項分布を含む独立成分分布の結合分布を計算することができる.
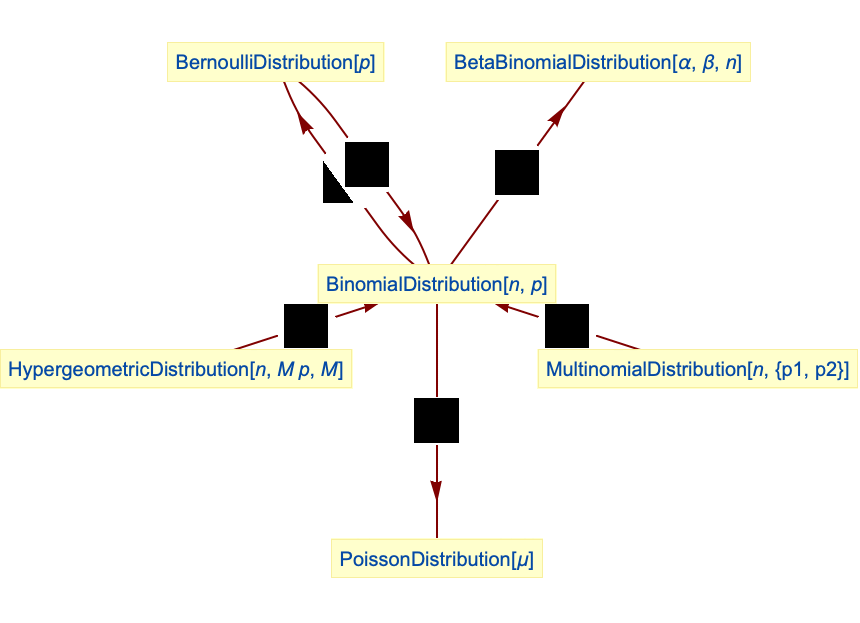
- BinomialDistributionは,数多くの他の統計分布と関係がある.例えば,BinomialDistribution[1,p]は,値
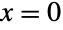 および
および 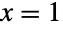 において,BernoulliDistribution[p]と厳密に等しく,BernoulliDistribution[p]に従って分布している n 個の独立変数の合計はBinomialDistribution[n,p]に従って分布している.同様に,BinomialDistribution[t,p]はBinomialProcess[p][t]と同じPDFを持つ.この特性は,BinomialDistribution[t,p]が厳密にSliceDistribution[BinomialProcess[p],t]であることによる.BinomialDistribution[n,p]はまた,いくつかの分布についての極限分布である.特に,BinomialDistribution[n,p]は,固定した p の値について,n がInfinityに近付く(ただし,
において,BernoulliDistribution[p]と厳密に等しく,BernoulliDistribution[p]に従って分布している n 個の独立変数の合計はBinomialDistribution[n,p]に従って分布している.同様に,BinomialDistribution[t,p]はBinomialProcess[p][t]と同じPDFを持つ.この特性は,BinomialDistribution[t,p]が厳密にSliceDistribution[BinomialProcess[p],t]であることによる.BinomialDistribution[n,p]はまた,いくつかの分布についての極限分布である.特に,BinomialDistribution[n,p]は,固定した p の値について,n がInfinityに近付く(ただし,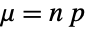 ,
,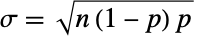 )につれてNormalDistribution[μ,σ]に収束し,n がInfinityに,p が0に近付くにつれて離散化された PoissonDistribution[p]に収束する.これに対し,HypergeometricDistribution[n,p]は,p がInfinityに近付くにつれてBinomialDistribution[n,p]に限定する.BinomialDistributionはMultinomialDistributionの2変数の形であり,BetaBinomialDistributionの構成成分であり,NegativeBinomialDistributionと自然に関係している.
)につれてNormalDistribution[μ,σ]に収束し,n がInfinityに,p が0に近付くにつれて離散化された PoissonDistribution[p]に収束する.これに対し,HypergeometricDistribution[n,p]は,p がInfinityに近付くにつれてBinomialDistribution[n,p]に限定する.BinomialDistributionはMultinomialDistributionの2変数の形であり,BetaBinomialDistributionの構成成分であり,NegativeBinomialDistributionと自然に関係している.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
極限値は標準NormalDistributionの尖度の値である:
無次元のQuantityを使ってBinomialDistributionを定義する:
アプリケーション (12)
BinomialDistributionのCDFは右連続関数の例である:
フリースローの成功確率が75%のバスケットボール選手がいる.10回のフリースローのシミュレーションを行う:
この選手が試合のフリースローで3回に2回成功する確率を求める:
この選手が5回のフリースローで最後の2回成功する確率を求める:
n 回のフリースローがある試合での期待される成功回数を求める:
打率0.300の野球選手がいる.5打席のシミュレーションを行う:
この選手が3回打席に立った場合の期待されるヒット数を求める:
ある薬が30%のケースで有効であると証明された,患者4人のうち少なくとも3人に有効である確率はどうなるだろうか:
公正なコインを n 回はじいた場合に表が出る回数はBinomialDistributionでモデル化することができる:
100回コインをはじいた場合に表が60回から80回出る確率を計算する:
不正なコインで表が出る確率が0.6だとした場合は以下のようになる:
航空機のエンジンに不具合が生じる確率は p である.2/4以下の割合で不具合が生じる場合を計算する:
4つのエンジンを選んだ方が2つのエンジンよりも優れている場合を考える:
3つのマイクロプロセッサを有しそのうちの1つが機能する限り使えるように設計された三重冗長性を使うシステムがある.1つのマイクロプロセッサが ![]() 秒後に使用可能な確率は
秒後に使用可能な確率は ![]() である.
である.![]() 秒たってもシステムが使用可能な確率を求める:
秒たってもシステムが使用可能な確率を求める:
各プロセッサの故障までの平均時間が ![]() であるとして,システムが99%未満の確率で動作するようになる時期を求める:
であるとして,システムが99%未満の確率で動作するようになる時期を求める:
チェスのチャンピオンであるガルリ・カスパロフがトーナメントで同時に100人のアマチュアを相手にしてチェスを行う.このような場合に彼が負ける確率は約1%であると見積もることができる.彼が0,2,5,10ゲームに負ける確率を求める:
チャンピオンが5ゲームを行う場合について同じ計算をする.ただし,対戦相手はより強く,チャンピオンが負ける確率は10%である:
n 個の記号の文字列からなるパケットがノイズの多い通信路を通して送られた.各記号が正しく送られない確率は![]() である.パケットが正しく送られない確率が
である.パケットが正しく送られない確率が![]() より小さくなる n を求める:
より小さくなる n を求める:
各顧客があるサービスを確率 p で使っている場合に n 人のうち ![]() 人の顧客がサービスを必要とする確率を求める:
人の顧客がサービスを必要とする確率を求める:
同時に ![]() (キャパシティ)を超えるサービスのリクエストがある確率を計算する:
(キャパシティ)を超えるサービスのリクエストがある確率を計算する:
![]() で
で ![]() のときにサービスが受けられる確率をさまざまなキャパシティ
のときにサービスが受けられる確率をさまざまなキャパシティ ![]() について計算する:
について計算する:
99.9%の確率でサービスが受けられる最小のキャパシティ ![]() を求める:
を求める:
2人のプレーヤーがサイコロを振っている.両方の目の合計が10に満たない場合は2番目のプレーヤーが4セントを受け取り,それ以外場合は最初のプレーヤーが9セント受け取る.このゲームは公平と言えるだろうか:
1ゲームあたりの平均スコアが等しくないのでこのゲームは公平ではない:
特性と関係 (9)
BinomialDistribution[n,p]は ![]() で正規分布に収束する:
で正規分布に収束する:
![]() のBinomialDistributionはBernoulliDistributionに等しい:
のBinomialDistributionはBernoulliDistributionに等しい:
BernoulliDistributionを示す n 個の独立変数の和は二項分布を示す:
BinomialDistributionはHypergeometricDistributionの母集団の上限を無限にしたものである:
n が大きく p が小さい場合,BinomialDistributionはPoissonDistributionに近付く:
BetaBinomialDistributionはBinomialDistributionとBetaDistributionを混合したものである:
考えられる問題 (3)
テキスト
Wolfram Research (2007), BinomialDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BinomialDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "BinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BinomialDistribution.html.
APA
Wolfram Language. (2007). BinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BinomialDistribution.html