BinomialDistribution[n,p]
表示试验次数为 n、成功概率为 p 的二项分布.


BinomialDistribution
BinomialDistribution[n,p]
表示试验次数为 n、成功概率为 p 的二项分布.
更多信息
- 在二项分布中,值
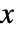 取从 0 到 n 的整数时,其概率为
取从 0 到 n 的整数时,其概率为 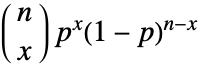 . »
. » - BinomialDistribution 允许 n 为任何非负整数.
- BinomialDistribution 允许 n 和 p 为无量纲的量. »
- BinomialDistribution 可与 Mean、CDF 和 RandomVariate 等函数一起使用. »
背景
- BinomialDistribution[n,p] 表示了一个定义在整数值
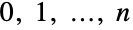 上,参数为非负实数 p(
上,参数为非负实数 p(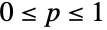 )的离散统计分布,即二项分布. 二项分布的离散概率密度函数(PDF)是单峰形状的,在均值
)的离散统计分布,即二项分布. 二项分布的离散概率密度函数(PDF)是单峰形状的,在均值 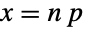 处取得峰值. 参数 n 和 p 决定了 PDF 的高度、水平位置及偏斜度.
处取得峰值. 参数 n 和 p 决定了 PDF 的高度、水平位置及偏斜度. - 对二项分布的研究可以追溯到十八世纪初雅各布·伯努利的工作,这使它成为被研究过的最古老的分布之一. 二项分布被设计用来模拟抛掷独立的 n 枚一模一样的(公平或不公平的)硬币的行为,独立采样,顺序替换. 传统上,p 被认为是试验“成功”的概率,而
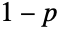 就是“失败”的概率. 用掷硬币做比喻,
就是“失败”的概率. 用掷硬币做比喻,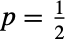 对应的就是抛掷公平的硬币.
对应的就是抛掷公平的硬币. - 尽管定义非常简单,二项分布是许多更复杂的数学概念的基础. 例如,二项分布可被认为是成功概率为 p 的有限 n 级伯努利过程(即由有限多个独立同分布(i.i.d.)的依据 BernoulliDistribution[p] 分布的随机变量组成的离散时间随机过程)成功率的分布. 同样的,二项分布还是二项过程(BinomialProcess)的切片分布(SliceDistribution). 二项过程是一个由有限多个独立同分布的服从二项分布的随机变量组成的离散时间,离散状态的随机过程,其时间服从几何分布(GeometricDistribution). 此外,许多现实世界的场景可以用二项过程模拟,比如投掷 n 面的(公平或不公平)的骰子得到特定值的概率. 在迁移模式和特定排队模型的研究中也意外的发现它们和二项分布之间有联系.
- RandomVariate 可被用于给出二项分布的一个或多个机器精度或任意精度(后者可用 WorkingPrecision 选项指定)的伪随机变量. Distributed[x,BinomialDistribution[n,p]],更简洁的写法是 xBinomialDistribution[n,p],可被用于声明随机变量 x 是二项分布的. 这样一个声明之后可用在如 Probability、NProbability、Expectation 以及 NExpectation 这样的函数中.
- 概率密度函数和累积分布函数可用 PDF[BinomialDistribution[n,p],x] 和 CDF[BinomialDistribution[n,p],x] 求得. 平均数、中位数、方差、原点矩及中心矩可分别用 Mean、Median、Variance、Moment 和 CentralMoment 计算. 这些量都可以通过 DiscretePlot 可视化.
- DistributionFitTest 可被用于测试给定的数据集是否与二项分布一致,EstimatedDistribution 可被用于根据给定数据估算二项参数化分布,而 FindDistributionParameters 可拟合数据和二项分布. ProbabilityPlot 可被用于生成给定数据的 CDF 相对于符号二项分布的 CDF 的图线,而 QuantilePlot 可被用于生成给定数据的分位数相对于符号二项分布的分位数的图线.
- TransformedDistribution 可被用于表示转换的二项分布,CensoredDistribution 可被用于表示删截后位于上限值和下限值之间的值分布,而 TruncatedDistribution 可被用于表示截断后位于上限值和下限值之间的值分布. CopulaDistribution 可被用于建立包含了二项分布的高维分布,而 ProductDistribution 可被用于计算包括二项分布在内的,若干个独立分量的联合分布.
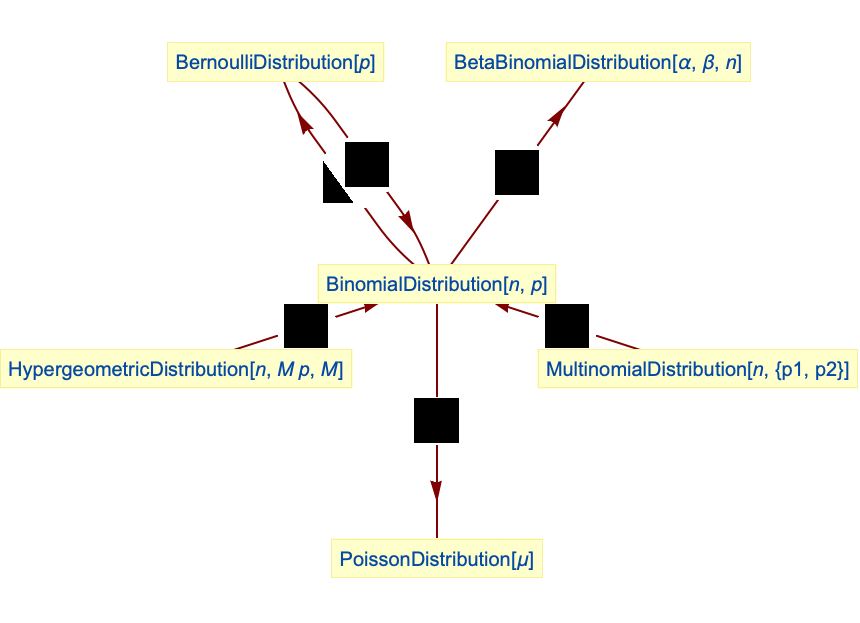
- BinomialDistribution 与许多其它统计分布密切相关. 例如 BinomialDistribution[1,p] 在
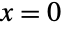 和
和 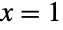 时恰好等于 BernoulliDistribution[p],而 n 个分布服从 BernoulliDistribution[p] 的独立随机变量之和的分布服从 BinomialDistribution[n,p]. 类似的,BinomialDistribution[t,p] 与 BinomialProcess[p][t] 有着相同的 PDF,这是因为 BinomialDistribution[t,p] 正好等于 SliceDistribution[BinomialProcess[p],t]. BinomialDistribution[n,p] 还是一些分布的极限分布. 特别的,当 n 趋向于 Infinity 而
时恰好等于 BernoulliDistribution[p],而 n 个分布服从 BernoulliDistribution[p] 的独立随机变量之和的分布服从 BinomialDistribution[n,p]. 类似的,BinomialDistribution[t,p] 与 BinomialProcess[p][t] 有着相同的 PDF,这是因为 BinomialDistribution[t,p] 正好等于 SliceDistribution[BinomialProcess[p],t]. BinomialDistribution[n,p] 还是一些分布的极限分布. 特别的,当 n 趋向于 Infinity 而 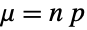 且
且 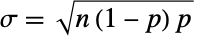 时,对于固定的 p,BinomialDistribution[n,p] 收敛于 NormalDistribution[μ,σ],当 n 趋向于 Infinity 且 p 趋向于 0 时则收敛于离散化后的 PoissonDistribution[p],而 HypergeometricDistribution[n,p] 在 p 趋向于 Infinity 时的极限为 BinomialDistribution[n,p]. BinomialDistribution 是 MultinomialDistribution 的双变量情形,是 BetaBinomialDistribution 的组成部分,还和 NegativeBinomialDistribution 有着天然的联系.
时,对于固定的 p,BinomialDistribution[n,p] 收敛于 NormalDistribution[μ,σ],当 n 趋向于 Infinity 且 p 趋向于 0 时则收敛于离散化后的 PoissonDistribution[p],而 HypergeometricDistribution[n,p] 在 p 趋向于 Infinity 时的极限为 BinomialDistribution[n,p]. BinomialDistribution 是 MultinomialDistribution 的双变量情形,是 BetaBinomialDistribution 的组成部分,还和 NegativeBinomialDistribution 有着天然的联系.
范例
打开所有单元 关闭所有单元范围 (8)
极限值是标准 NormalDistribution 的峰度值:
使用无量纲的 Quantity 来定义 BinomialDistribution:
应用 (12)
BinomialDistribution 的 CDF 是右连续函数的一个例子:
一名篮球运动员有0.75的百分比得到一次罚球. 以下模拟 10 次罚球:
一种药物已被证明对于 30% 的病例有效. 求对于4个病人,该药物对至少其中3个病人有效的概率:
在 n 次投掷硬币中,假设正反面出现的概率相等,则出现正面的次数可以使用 BinomialDistribution 建模:
计算在100次投掷硬币中,正面出现次数在60到80之间的概率:
现在,假设对于一个正反面出现概率不同的硬币,正面出现的概率为 0.6:
一个飞机引擎失效的概率为 p;计算4个引擎中,不超过2个失效的概率:
一个系统具有使用三个微处理器的三重冗余,并且只要有一个处理器还在工作,就可以运作. ![]() 秒后微处理器仍然运作的概率是
秒后微处理器仍然运作的概率是 ![]() . 求
. 求 ![]() 秒后系统仍然运作的概率:
秒后系统仍然运作的概率:
对每个处理器来说,平均失效时间是 ![]() ,求系统有少于 99% 的概率工作的时间:
,求系统有少于 99% 的概率工作的时间:
加里卡斯帕罗夫,国际象棋世界冠军,在一次联赛中同时与100个业余选手对决. 据估计,在这样的比赛中,他失败的概率约为 1%. 求他失败 0、2、5 和10场比赛的概率:
当他参加5场比赛时,执行相同的计算,但此时假设他失败的概率是10%:
一个包含由 n 个符号组成的字符串的数据包在一个有噪声的频道传播. 每个符号错误传播的概率为 ![]() . 求 n,使得不正确的数据包传播的概率小于
. 求 n,使得不正确的数据包传播的概率小于 ![]() :
:
如果每个顾客需要服务的概率为 p,求 n 个顾客中有 ![]() 个需要服务的概率,
个需要服务的概率,
两个玩家掷骰子. 如果两个数字的总和小于10,那么第二个玩家得到4分钱,否则,第一个玩家得到9分钱. 这个游戏公平吗?:
属性和关系 (9)
在 ![]() 时,BinomialDistribution[n,p] 收敛于正态分布:
时,BinomialDistribution[n,p] 收敛于正态分布:
![]() 的 BinomialDistribution 等于 BernoulliDistribution:
的 BinomialDistribution 等于 BernoulliDistribution:
服从 BernoulliDistribution 的 n 个独立变量的和是二项分布:
BinomialDistribution 是 HypergeometricDistribution 的无穷对象的总体:
对于较大的 n 和较小的 p,BinomialDistribution 趋近于 PoissonDistribution:
BetaBinomialDistribution 是 BinomialDistribution 和 BetaDistribution 的混合分布:
可能存在的问题 (3)
技术笔记
-
▪
- 离散分布
文本
Wolfram Research (2007),BinomialDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BinomialDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2007. "BinomialDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/BinomialDistribution.html.
APA
Wolfram 语言. (2007). BinomialDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BinomialDistribution.html 年
BibTeX
@misc{reference.wolfram_2025_binomialdistribution, author="Wolfram Research", title="{BinomialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BinomialDistribution.html}", note=[Accessed: 14-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_binomialdistribution, organization={Wolfram Research}, title={BinomialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BinomialDistribution.html}, note=[Accessed: 14-February-2026]}