ComplexArrayPlot[array]
生成一个绘图,在一个离散方形阵列图中显示数组 array 中的复数值 zij,其中用颜色表示 Arg[zij],用明暗表示 Abs[zij].




ComplexArrayPlot
ComplexArrayPlot[array]
生成一个绘图,在一个离散方形阵列图中显示数组 array 中的复数值 zij,其中用颜色表示 Arg[zij],用明暗表示 Abs[zij].
更多信息和选项







- ComplexArrayPlot 用于可视化复数表.
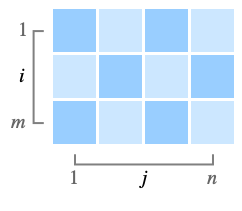
- ComplexArrayPlot[array] 默认情况下会安排 mn 维度数组 array 中连续行顺着页面往下排列,连续列顺着页面横向排列,就像普通的表格或网格的格式一样.
- ComplexArrayPlot 会在 Arg[zij] 的值上使用循环颜色函数,并使用明暗来表示 Abs[zij] 的值. 模数较大的复数比模数较小的复数更明亮.
- 在 ComplexArrayPlot[array] 中,array 可有如下格式:
-
{{z11,z12,…,z1n},…,{zm1,zm2,…,zmn}} 值 zij SparseArray 以普通数组给出的值 NumericArray 以普通数组给出的值 Dataset 以普通数组给出的值 - 下列特殊条目可用于 zij:
-
None 背景颜色 颜色指令 指定颜色 - 若 array 长短不一,则较短的行会被看做是用背景在右边进行填充.
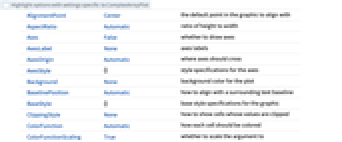
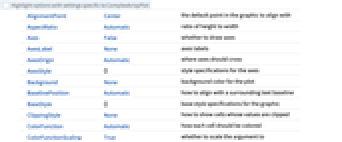
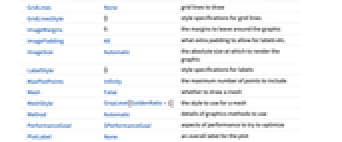
- ComplexArrayPlot 的选项与 Graphics 很像,有如下的添加和变化: [所有选项的列表]
-
AspectRatio Automatic 高与宽的比率 ClippingStyle None 如何显示数值被剪切的单元 ColorFunction Automatic 如何为每个单元上色 ColorFunctionScaling True 是否对 ColorFunction 的参数进行缩放 ColorRules Automatic 根据决定颜色的规则 DataRange All 假设的 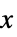 和
和 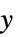 值的范围
值的范围DataReversed False 是否倒转行的顺序 Frame Automatic 是否为图形绘制边框 FrameLabel None 行和列的标签 FrameTicks None 边框中要包括的刻度 MaxPlotPoints Infinity 最多可以包含多少个点 Mesh False 是否绘制网格 MeshStyle GrayLevel[GoldenRatio-1] 网格使用的样式 PerformanceGoal $PerformanceGoal 优化的目标 PlotLegends None 数据集的图例 PlotRange All 绘制的值的范围 PlotTheme $PlotTheme 绘图的整体主题 TargetUnits Automatic 绘图中展示的单位 - ColorRules 给出的规则被应用于每个单元的
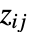 . 规则可以包括模式.
. 规则可以包括模式. - 如果没有应用 ColorRules 中的任何规则,则使用 ColorFunction 决定颜色.
- 如果使用默认设置 ColorRules->Automatic,则会使用明确的设置 ColorFunctioncfunc 而非 ColorRules.
- ColorFunction->{cfunc,sfunc} 使用 cfunc 生成基础颜色,并使用 sfunc 调整颜色以突出显示特征.
- sfunc 的可能的已命名设置包括:
-
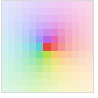
Automatic 基于 Abs[z] 自动调整明暗 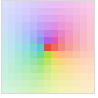
"MaxAbs" Abs[z] 较大值的浅色调 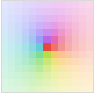
"LocalMaxAbs" Abs[z] 的上四分位数的的浅色调 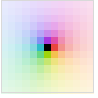
"GlobalAbs" 与 Abs[z] 从小到大的值对应的由暗到亮的色调 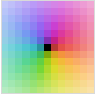
"QuantileAbs" 基于 Abs[z] 的分位数的由暗到亮的色调 
"CyclicLogAbs" Log[Abs[z]] 的循环的由暗到亮的色调 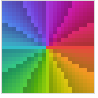
"CyclicArg" Arg[z] 的循环的由暗到亮的色调 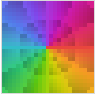
"CyclicLogAbsArg" Log[Abs[z]] 和 Arg[z] 的循环的色调 
"CyclicReImLogAbs" Re[z] 和 Im[z] 的暗色环,Log[Abs[z]] 的浅色环 
"ShiftedCyclicLogAbs" 超过特定阈值后的 Log[Abs[z]] 的循环的色调 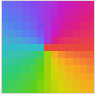
None 不改变色调 - 默认情况下,ColorFunction 中的函数由缩放版的 Re[z]、Im[z]、Abs[z] 和 Arg[z] 提供.
- 若某个特定单元格的颜色为 None,则该单元格用背景色进行渲染.
- 若未为某个特定的单元格决定颜色,则该单元格会以默认深红色渲染.
- 设置 DataReversed->True,则倒转行的顺序,这样行从底部到顶部排序,最后一行排在最上面.
- 设置 FrameTicks->Automatic,刻度通常放在四舍五入的整数位置,通常在 5 或 10 的倍数处.
- 设置 FrameTicks->All,刻度通常放在最小和最大的
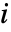 和
和 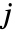 处.
处. - 在明确的 FrameTicks 设置下,刻度的坐标用于指代
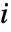 和
和 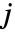 .
. - PlotRange 可以有如下格式:
-
zmax 在 0 到 zmax 之间显示 Abs[zij] 的值 {zmin,zmax} 在 zmin 和 zmax 之间显示 Abs[zij] 的值 {rangei,rangej} 显示 zij 的值,其中 i 在 rangei 中且 j 在 rangej 中 {rangei,rangej,rangez} 显示 zij 的值,其中 i 在 rangei 中,j 在 rangej 中且 zij 在 rangez 中 - 数组指数范围为从 rangei 到 rangej,且可以有如下形式:
-
{min,max} 包括 min 和 max 之间的指数 All 包括所有指数 - PlotLegends 的一般设置包括:
-
None 没有图例 Automatic 自动决定图例 Placed[lspec,…] 明确图例的位置 - Mesh->True 在数组的每个单元格之间绘制网格线.
- Mesh->{mi,mj} 分别为
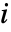 和
和 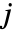 方向给出网格格式说明.
方向给出网格格式说明. - 默认设置 Frame->Automatic,边框仅在 Mesh->False 时绘制.
- 为了结合其他图形,使用数组元素
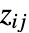 覆盖中心坐标位置为
覆盖中心坐标位置为 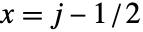 ,
,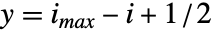 的单位正方形.
的单位正方形. - 设置 DataRange->{{xmin,xmax},{ymin,ymax}} 说明连续单元格的中心应该处于 xmin 与 xmax 之间的水平方向和 ymin 与 ymax 之间的垂直方向的等距位置. 默认设置 DataReversed->False,
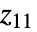 的中心在 {xmin,ymax}.
的中心在 {xmin,ymax}. - 默认设置 DataRange->All 且 DataReversed->False,数组元素
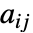 会被用来覆盖中心坐标位置为
会被用来覆盖中心坐标位置为 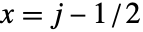 ,
, 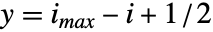 的单位正方形.
的单位正方形.
所有选项的列表


范例
打开所有单元 关闭所有单元范围 (14)
数据 (8)
默认情况下,颜色会伴随着参数从 ![]() (青蓝)到
(青蓝)到 ![]() (红色)到
(红色)到 ![]() (青蓝)的变化而改变:
(青蓝)的变化而改变:
带有值 None 的单元格用背景色进行渲染:
演示 (6)
选项 (71)
AspectRatio (4)
Axes (4)
Background (4)
Background 通常只可在边缘看到:
只要明确输入了 None,就能直接看到背景颜色::
对于在绘图范围外的值,默认情况下也可以直接看到 Background:
ClippingStyle 覆写背景颜色:
ColorFunction (9)
ColorFunctionScaling (3)
ColorRules (6)
如果不应用任何颜色规则的话,则会使用 ColorFunction:
MaxPlotPoints (1)
使用 MaxPlotPoints 可以在每个方向上明确限制绘制的元素的数量:
PlotLegends (5)
PlotLegends 自动识别有名称的 ColorFunction:
PlotLegends 不会识别用户自定义的 ColorFunction,但是用户仍然可以构建合适的图例:
使用 Placed 改变图例的位置:
应用 (18)
傅立叶变换 (6)
展示原始数据和其傅立叶变换. 在第二个绘图中,第四行和第六列(从左上角开始数)的浅色方块告诉我们对应的频率分别为 3 和 5:
使用 ColorRules 为傅立叶变换设置阈值:
绘制了傅立叶变换的幅度,但这并未显示可能有用的相位信息. 观察中间的绘图中其他的信息:
注意傅立叶变换中 ComplexArrayPlot 的变化和 ArrayPlot 没有变化:
吸引盆 (2)
矩阵光谱 (2)
迭代系统 (3)
属性和关系 (5)
ComplexArrayPlot 通过参数为复值上色,并通过像 ComplexPlot 这样的模数添加阴影:
ComplexArrayPlot 类似应用于复值参数的 ArrayPlot 和 MatrixPlot:
Grid 排列元素的方法与 ComplexArrayPlot 一样:
Raster 将与 ComplexArrayPlot 有关的元素上下倒转排列:
ArrayPlot3D 可用于数据的三维数组:
相关指南
-
▪
- 复数可视化
文本
Wolfram Research (2020),ComplexArrayPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexArrayPlot.html.
CMS
Wolfram 语言. 2020. "ComplexArrayPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ComplexArrayPlot.html.
APA
Wolfram 语言. (2020). ComplexArrayPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ComplexArrayPlot.html 年
BibTeX
@misc{reference.wolfram_2025_complexarrayplot, author="Wolfram Research", title="{ComplexArrayPlot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ComplexArrayPlot.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_complexarrayplot, organization={Wolfram Research}, title={ComplexArrayPlot}, year={2020}, url={https://reference.wolfram.com/language/ref/ComplexArrayPlot.html}, note=[Accessed: 16-February-2026]}