ElementwiseLayer
一変数関数 f を入力配列のすべての要素に適用するネット層を表す.
ElementwiseLayer["name"]
"name"で指定された関数を適用する.
詳細とオプション


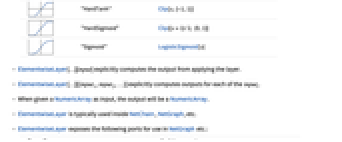
- 関数 f は,Ramp,LogisticSigmoid,Tan,Tanh,ArcTan,ArcTanh,Sin,Sinh,ArcSin,ArcSinh,Cos,Cosh,ArcCos,ArcCosh,Cot,Coth,ArcCot,ArcCoth,Csc,Csch,ArcCsc,ArcCsch,Sec,Sech,ArcSec,ArcSech,Haversine,InverseHaversine,Gudermannian,InverseGudermannian,Log,Exp,Sqrt,CubeRoot,Abs,Gamma,LogGamma,Erf,InverseErf,Erfc,InverseErfc,Round,Floor,Ceiling,Sign,FractionalPart,IntegerPart,Unitize,KroneckerDeltaのいずれでもよい.
- 一般に,f は,単一の引数に適用されたときに,Ramp,LogisticSigmoid等と,Plus,Subtract,Times,Divide,Power,Surd,Min,Max,Clip,Mod,Threshold,Chopと任意の数の組合せ,およびIf,And,Or,Which,Piecewise,Equal,Greater,GreaterEqual,Less,LessEqual,Unequal,Negative,NonNegative,Positive,NonPositive,PossibleZeroQを使った論理演算を返す任意のオブジェクトでよい.
- ElementwiseLayerは,"name"について次の値をサポートする.
-
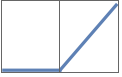
"RectifiedLinearUnit" または "ReLU" Ramp[x] 
"ExponentialLinearUnit" または "ELU" x≥0のとき x x<0のときExp[x]-1 
"ScaledExponentialLinearUnit" または "SELU" x >= 0のとき1.0507 x x<0のとき1.7581 (Exp[x]-1) 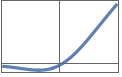
"GaussianErrorLinearUnit"または "GELU" 0.5 x(1+Erf[x/Sqrt[2]]) 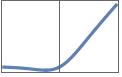
"Swish" x LogisticSigmoid[x] 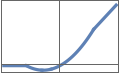
"HardSwish" x Min[Max[x+3,0],6] / 6 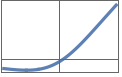
"Mish" x Tanh[Log[1+Exp[x]]] 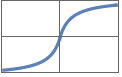
"SoftSign" x/(1+Abs[x]) 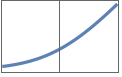
"SoftPlus" Log[Exp[x]+1] 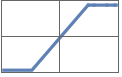
"HardTanh" Clip[x,{-1,1}] 
"HardSigmoid" Clip[(x+1)/2, {0,1}] 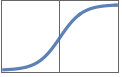
"Sigmoid" LogisticSigmoid[x] - ElementwiseLayer[…][input]は,層を適用することで明示的に出力を計算する.
- ElementwiseLayer[…][{input1,input2,…}]は,各 inputiについて明示的に出力を計算する.
- NumericArrayが入力として与えられると,出力はNumericArrayになる.
- ElementwiseLayerは,NetChain,NetGraph等で使われることが多い.
- ElementwiseLayerはNetGraph等で使うために次のポートを開放する.
-
"Input" 任意階数の配列 "Output" 入力と同じ次元の配列 - より大きいネットの他の層から推測できない場合は,オプション"Input"->{n1,n2,…}を使ってElementwiseLayerの入力次元を固定することができる.
- Options[ElementwiseLayer]は層を構築する際のデフォルトオプションのリストを与える.Options[ElementwiseLayer[…]]はデータについて層を評価する際のデフォルトオプションのリストを与える.
- Information[ElementwiseLayer[…]]は層についてのレポートを与える.
- Information[ElementwiseLayer[…],prop]はElementwiseLayer[…]の特性 prop の値を与える.使用可能な特性はNetGraphと同じである.
例題
すべて開くすべて閉じる例 (2)
スコープ (3)
「Hard Sigmoid」関数を計算するElementwiseLayerを作る:
サイズ3のベクトルを取るElementwiseLayerを作る:
この層は,ベクトルのバッチに適用されると自動的にそれに縫い込まれる:
ガウス分布を計算するElementwiseLayerを作る:
アプリケーション (3)
「Self-Normalizing Neural Networks", G. Klambauer et. al., 2017」にある16層深度の自己正規化ネットワークを,UCI文字集合について訓練する.データを取得する:
自己正規化ネットは入力データの平均が0で分散が1であると仮定する.テストを標準化してデータを訓練する:
訓練データのサンプルの平均と分散が,それぞれ0と1であることを確認する:
"AlphaDropout"で16層自己正規化ネットを定義する:
Classifyの"RandomForest"メソッドの確度と比較する:
分類ネットワークが「分離不可能な」問題を扱えるようにする.円 r=0.5で2つのクラスに分離された,円板上の点からなる合成訓練集合を作る:
2つのLinearLayer層とElementwiseLayerを使った確率への最終変換からなる層を作る:
LinearLayerはアフィン層なので,介在する非線形性なしで2つの層を積み重ねることは単一の層を使うことに等しい.平面上の単一の直線は,単一のLinearLayerのレベル集合である2つのクラスを分離することはできない.
2層間にTanh非線形性を有する同様のネットを訓練する:
バイナリ分類タスクに使うネットの出力は確率でなければならない.ElementwiseLayer[LogisticSigmoid]を使って任意のスカラーを取り,0と1の間の値を生成する.長さ2のベクトルを取りバイナリ予測を行うネットを作る:
特性と関係 (1)
NetChainまたはNetGraph内で適切な関数が指定されると,ElementwiseLayerが自動的に使われる:
考えられる問題 (3)
ElementwiseLayerは記号入力を受け付けない:
f の選び方によっては,入力が領域外に出てしまうのでエラーになる:
有理関数を使ってZeta関数を近似する:
この近似を使ってElementwiseLayerを構築する:
テキスト
Wolfram Research (2016), ElementwiseLayer, Wolfram言語関数, https://reference.wolfram.com/language/ref/ElementwiseLayer.html (2022年に更新).
CMS
Wolfram Language. 2016. "ElementwiseLayer." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/ElementwiseLayer.html.
APA
Wolfram Language. (2016). ElementwiseLayer. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ElementwiseLayer.html