ListSliceContourPlot3D

ListSliceContourPlot3D[farr,surf]

曲面 surf についてスライスされた三次元 surf の等高線プロットを生成する．

ListSliceContourPlot3D[{{x1,y1,z1,f1},{x2,y2,z2,f2},…},surf]

点{xi,yi,zi}における fiの値についてのスライス等高線プロットを生成する．

ListSliceContourPlot3D[…,{surf1,surf2,…}]

複数のスライス surf1, surf2, …上でスライス等高線プロットを生成する．

詳細とオプション

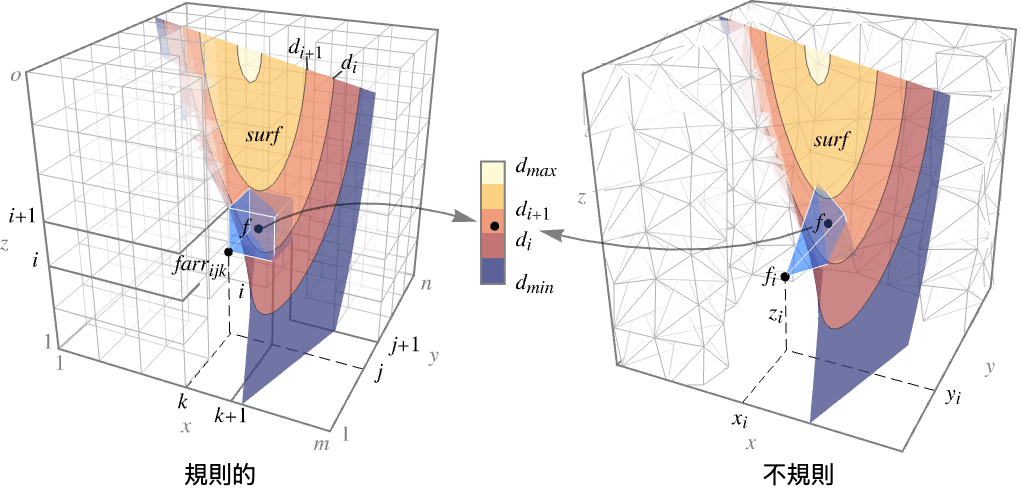
  • ListSliceContourPlot3Dは，立体の表面に滑らかな等高線を与える．
  • ListSliceContourPlot3Dは，曲面 surf 上に，補間されたされた関数 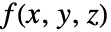が一定の値 d1，d2等を持つレベル集合に対応する等曲線を構築する．デフォルトで，値が diから di+1までの領域が簡単に識別できるように曲線間の領域は陰影付される．
  • 規則的なデータについては，関数 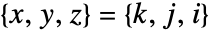は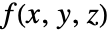で値 farr[[i,j,k]]を持つ．
  • 不規則データについて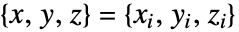は，はで値 fiを持つ．
  • 次は，領域 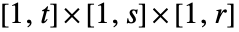が規則的なデータについてはデカルト積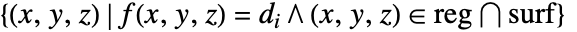，不規則データについては{{x1,y1,z1},…,{xn,yn,zn}}の凸包である曲面を可視化する．
  • 次の基本的なスライス面 surfiを与えることができる．
  • Automaticスライス面を自動的に決定する
    "CenterPlanes"中心を通る座標平面
    "BackPlanes"プロットの後ろの座標平面
    "XStackedPlanes" 軸に沿って積み重ねられた座標平面
    "YStackedPlanes" 軸に沿って積み重ねられた座標平面
    "ZStackedPlanes" 軸に沿って積み重ねられた座標平面
    "DiagonalStackedPlanes"対角上に軸に沿って積み重ねられた座標平面
    "CenterSphere"中心の球
    "CenterCutSphere"切り取られたウェッジがある球
    "CenterCutBox"切り取られた象限があるボックス
  • ListSliceContourPlot3D[data]はListSliceContourPlot3D[data,Automatic]に等しい．
  • 基本的なスライス面には次のパラメータ化を使うことができる．
  • {"XStackedPlanes",n},n 個の等間隔の平面を生成
    {"XStackedPlanes",{x1,x2,…}}x=xiについての平面を生成
    {"CenterCutSphere",ϕopen}視点に面したカット角 ϕopen
    {"CenterCutSphere",ϕopen,ϕcenter} 平面上の中心角が ϕcenterのカット角 ϕopen
  • "YStackedPlanes"および "ZStackedPlanes"は"XStackedPlanes"についての指定に従う．追加的な特徴はスコープの例で示す．
  • 次の一般的なスライス面 surfiを使うことができる．
  • surfaceregion3Dにおける二次元領域，例：Hyperplane
    volumeregionsurfiが境界面とみなされる3Dにおける三次元領域，例：Cuboid
  • スライス面 surfiには次のラッパーを使うことができる．
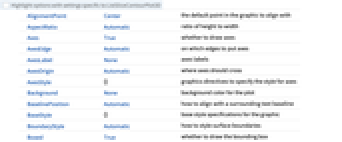
  • Annotation[surf,label]注釈を与える
    Button[surf,action]曲面がクリックされた際に実行する動作を定義
    EventHandler[surf,…]曲面の一般的なイベントハンドラを定義
    Hyperlink[surf,uri]曲面がハイパーリンクとして動作するようにする
    PopupWindow[surf,cont]曲面にポップアップウィンドウを付ける
    StatusArea[surf,label]曲面上にマウスが来た場合にステータスエリアに表示
    Tooltip[surf,label]曲面に任意のツールチップを付ける
  • ListSliceContourPlot3Dには，Graphics3Dと同じオプションに以下の追加・変更を加えたものが使える． [全オプションのリスト]
  • AxesTrue軸を描くかどうか
    BoundaryStyle Automatic表面の境界にどのようにスタイル付けするか
    BoxRatios {1,1,1}境界3Dボックスの比
    ClippingStyle NonePlotRangeで切り取られた値をどのように描画するか
    ColorFunction Automaticプロットにどのように彩色するか
    ColorFunctionScaling TrueColorFunctionの引数をスケールするかどうか
    Contours Automatic各曲面に何本の／どのような等高線を表示するか
    ContourShading Automatic等高線間の領域にどのように陰影付けするか
    ContourStyle Automatic等高線のスタイル
    DataRange Automaticデータとして仮定する x，y，z の値の範囲
    PerformanceGoal $PerformanceGoalパフォーマンスのどの面について最適化するか
    PlotLegends None色勾配の凡例
    PlotPoints Automatic各方向のスライス面 surfiの近似サンプル数
    PlotRange {Full,Full,Full,Automatic}含める f あるいは他の値の範囲
    PlotTheme $PlotThemeプロットの全体的なテーマ
    RegionFunction (True&)点を含めるかどうかの決め方
    ScalingFunctions None個々の座標のスケール方法
    TargetUnits Automatic使用する所望の単位
  • デフォルトで，ColorFunctionには f のスケールされた値が渡される．
  • デフォルトで，RegionFunctionには x，y，z，f が渡される．
  • 次元{r,s,t}の farr について，DataRangeAutomaticという設定はDataRange{{1,r},{1,s},{1,t}}に等しい．
  • 次は，ScalingFunctionsの可能な設定である．
  • sff 等高線の値をスケールする
    {sx,sy,sz}x，y，z の各軸をスケールする
    {sx,sy,sz,sf}x，y，z の各軸と f 等高線の値をスケールする
  • 次は，よく使われるスケーリング関数 s である．
  • "Log"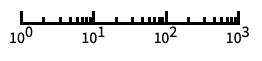自動目盛ラベル付きの対数スケール
    "Log10"10のベキ乗に目盛がある10を底とする対数スケール
    "SignedLog"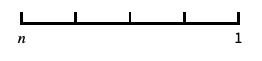0と負の数を含む対数に似たスケール
    "Reverse"座標の向きを逆にする

    • 全オプションのリスト

例題

すべて開くすべて閉じる

例  (2)

表面の集合上で値の配列の等高線をプロットする：

曲面 上に等高線をプロットする：

スコープ  (28)

表面  (9)

標準的なスライス面上に等高線プロットを生成する：

標準的な軸に並んだ積み重ねスライス面：

標準的な境界表面：

任意の表面領域に等高線をプロットする：

体積プリミティブ上にプロットすることは，RegionBoundary[reg]上にプロットすることに等しい：

曲面 上に等高線をプロットする：

複数の表面上に等高線をプロットする：

積み重ね表面の数を指定する：

中心切り取り球スライスの切取り角を指定する：

データ  (8)

個の値からなる規則的なデータについて，，， のデータは配列中のその位置を反映する：

DataRangeを使って明示的な ，， のデータ範囲を与える：

(, , , ) のタプルからなる不規則データの補間された等高線をプロットする：

データの値が与えられた点を示す：

SparseArrayで与えられた値の配列についての等高線をプロットする：

QuantityArrayで与えられた値の配列について，密度をプロットする：

Contoursを使って等高線の数を指定する：

あるいは，関数値 のリストを使って等高線を置く：

PlotPointsを使って表面のサンプリングを制御する：

関数が実数ではなくなる部分は除外される：

RegionFunctionを使って曖昧なスライスを露出させる：

プレゼンテーション  (11)

PlotThemeを使って即座に全体的なスタイリングを得る：

PlotLegendsを使ってさまざまな値についての色の棒を得る：

Axesで軸の表示を制御する：

AxesLabelを使って軸に，PlotLabelを使ってプロット全体にラベルを付ける：

ColorFunctionで，データ値によってプロットに彩色する：

ContourShadingを使って等高線の間の領域にスタイルを施す：

ContourStyleを使って等高線にスタイルを付ける：

BoundaryStyleでスライス面の境界にスタイルを付ける：

TargetUnitsは，可視化でどの単位を使うかを指定する：

軸を対数スケールにしたプロットを作成する：

方向の座標の向きを逆にする：

オプション  (40)

BoundaryStyle  (1)

BoundaryStyleでスライス面の境界にスタイルを付ける：

BoxRatios  (3)

デフォルトで，境界ボックスの辺は同じ長さになっている：

BoxRatios->Automaticを使って3D座標値の自然なスケールを示す：

境界ボックスの各側にカスタムの長さを使う：

ClippingStyle  (2)

切り取られた領域に彩色する：

Noneを使って切り取られた領域を取り除く：

ColorFunction  (3)

の値に従って等高線に彩色する：

ColorDataから名前付きの色勾配を使う：

のところに赤を使う：

ColorFunctionScaling  (2)

デフォルトで，スケールされた値が使われる：

ColorFunctionScaling->Falseを使ってスケールされていない値を得る：

Contours  (4)

自動等高線選択を使う：

等間隔の5本の等高線を使う：

明示的な等高線集合を指定する：

特定のスタイルの特定の等高線を使う：

ContourStyle  (1)

等高線を黄色にする：

ContourShading  (4)

ContourShadingAutomaticはColorFunctionから等高線領域の陰影付けを計算する：

陰影付けのスタイルを循環的に繰り返す：

2番目から始めて3番目ごとの等高線領域を空にする：

等高線間の領域を空にする：

DataRange  (2)

デフォルトで，データ範囲は配列の次元であるとみなされる：

データ範囲を明示的に指定する：

PerformanceGoal  (2)

高品質のプロットを生成する：

品質を犠牲にしてもパフォーマンスを優先する：

PlotLegends  (1)

PlotLegendsは，自動的にContoursとContourShadingを選ぶ：

PlotPoints  (1)

プロット点の数を多くすると，表面の離散化がより細かくなり，データの解釈もより詳しくなる：

PlotRange  (3)

デフォルトですべて(All)の等高線が示される：

選択された範囲を示す：

の値を含む選択された範囲を示す：

PlotTheme  (3)

詳しい格子線，メモリ，凡例があるテーマを使う：

任意のオプション設定でPlotTheme設定，この場合は面格子，が無効にされる：

さまざまなプロットテーマを比較する：

RegionFunction  (1)

あるいは の等高線のみを含める：

ScalingFunctions  (6)

デフォルトで，プロットはすべての方向が線形スケールになる：

軸が対数スケールのプロットを作成する：

方向の座標の向きを逆にする：

関数とその逆関数で定義されたスケールを使う：

スケーリング関数は変数によって定義されたスライスに適用される：

境界ボックスと相対的に定義されたスライスの表面はスケーリング関数の影響を受けない：

TargetUnits  (1)

QuantityArrayで指定された単位は，TargetUnitsで指定された単位に変換される：

アプリケーション  (10)

基本データ  (4)

で生成されたデータの等高線スライスをプロットする：

および から生成されたデータの等高線：

および から生成されたデータ：

および から生成されたデータ：

および から生成されたデータ：

および から生成されたデータ：

一変量関数の積であるからのデータ：

一変量関数と二変量関数であるおよび からのデータ：

三変量関数である の等高線スライスをプロットする：

指数関数の総和sum_ialpha_i exp(-TemplateBox[{{p, -, {p, _, i}}}, Norm]^2)の等高線スライスをプロットする：

ボックス内の点 をランダムに選択し，その等高線スライスをプロットする：

シミュレーションデータ  (4)

三変数の確率密度関数の等高線スライスをプロットする：

サンプルを取り関数をプロットする：

分布のシミュレーションを行い，ビン数を計算し，等高線スライスをプロットする：

二次元セルオートマトンの進化の等高線スライスをプロットする：

方向への時間進化で10世代ごとにサンプルを取る：

中心線に沿ったセルが時間とともにどのように進化するかを見ることもできる：

メンガー(Menger)のスポンジ配列を生成し，そこから等高線スライスをプロットする：

配列中の半径1の近傍の値の平均を取り等高線スライスをプロットすることで，ランダムな値の二次元配列の離散拡散モデルのシミュレーションを行う：

時間は 軸に沿って進化する．時点1，5，15のスナップショットを撮る：

経験的データ  (2)

タンパク質中の原子の位置をビンに入れ，そこから得られる等高線密度スライスをプロットする：

ピコメートル単位の軸で原子の集中を示す：

脳のMRIデータを可視化する：

特性と関係  (5)

表面上の連続密度にListSliceDensityPlot3Dを使う：

一定値の表面にListContourPlot3Dを使う：

データ値の完全体積可視化にListDensityPlot3Dを使う：

関数にSliceContourPlot3Dを使う：

2Dの等高線プロットにListContourPlotを使う：

考えられる問題  (1)

値が一定のスライス面はノイズが入って見える：

関数 は選択されたスライス面上で一定である：

別のスライス面を選ぶと関数の合理的な絵が得られる：

Wolfram Research (2015), ListSliceContourPlot3D, Wolfram言語関数， https://reference.wolfram.com/language/ref/ListSliceContourPlot3D.html （2022年に更新）.

テキスト

Wolfram Research (2015), ListSliceContourPlot3D, Wolfram言語関数， https://reference.wolfram.com/language/ref/ListSliceContourPlot3D.html （2022年に更新）.

CMS

Wolfram Language. 2015. "ListSliceContourPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/ListSliceContourPlot3D.html.

APA

Wolfram Language. (2015). ListSliceContourPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ListSliceContourPlot3D.html

BibTeX

@misc{reference.wolfram_2024_listslicecontourplot3d, author="Wolfram Research", title="{ListSliceContourPlot3D}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ListSliceContourPlot3D.html}", note=[Accessed: 13-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_listslicecontourplot3d, organization={Wolfram Research}, title={ListSliceContourPlot3D}, year={2022}, url={https://reference.wolfram.com/language/ref/ListSliceContourPlot3D.html}, note=[Accessed: 13-November-2024 ]}