SliceDensityPlot3D[f,surf,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
在切片曲面 surf 上,生成以 x、y、z 为函数的 f 的密度图.
SliceDensityPlot3D[f,surf,{x,y,z}∈reg]
将曲面限制在区域 reg 内.
SliceDensityPlot3D[f,{surf1,surf2,…},…]
在多个切片上生成密度图.




SliceDensityPlot3D
SliceDensityPlot3D[f,surf,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
在切片曲面 surf 上,生成以 x、y、z 为函数的 f 的密度图.
SliceDensityPlot3D[f,surf,{x,y,z}∈reg]
将曲面限制在区域 reg 内.
SliceDensityPlot3D[f,{surf1,surf2,…},…]
在多个切片上生成密度图.
更多信息和选项






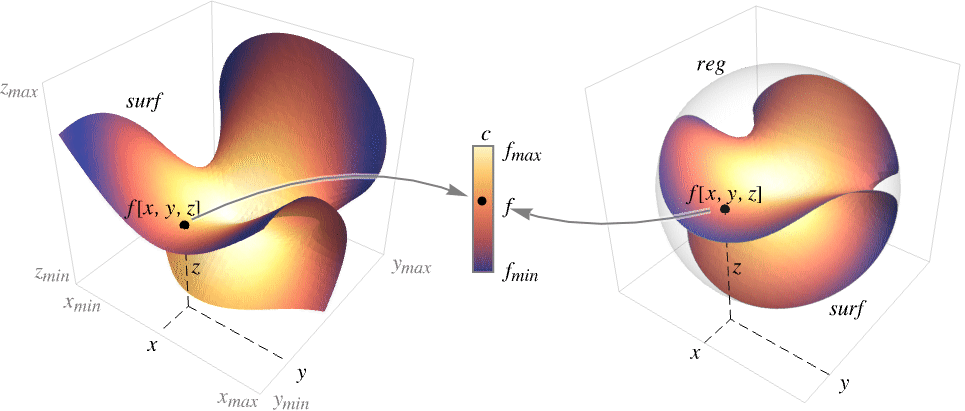
- SliceDensityPlot3D 在曲面 surf 上的 x、y 和 z 值处计算 f,并使用颜色函数
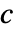 将每个值 f[x,y,z] 映射为一种颜色.
将每个值 f[x,y,z] 映射为一种颜色. - 绘图可视化了集合
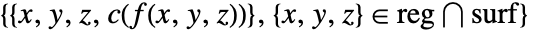 ,其中
,其中 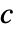 为颜色函数.
为颜色函数. - 可以给出以下基本切片曲面 surfi:
-
Automatic 自动确定切片曲面 
"CenterPlanes" 过中心点的坐标平面 
"BackPlanes" 图形后面的坐标平面 
"XStackedPlanes" 沿 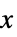 轴叠放的坐标平面
轴叠放的坐标平面
"YStackedPlanes" 沿 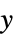 轴叠放的坐标平面
轴叠放的坐标平面
"ZStackedPlanes" 沿 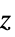 轴叠放的坐标平面
轴叠放的坐标平面
"DiagonalStackedPlanes" 沿对角线叠放的坐标平面 
"CenterSphere" 位于中心的球面 
"CenterCutSphere" 切去楔形块的球面 
"CenterCutBox" 八分之一被切掉的盒子 - SliceDensityPlot3D[f,{x,xmin,xmax},…] 等价于 SliceDensityPlot3D[f,Automatic,{x,xmin,xmax},…] 等.
- 以下参数化可用于基本切片曲面:
-
{"XStackedPlanes",n}, 生成 n 个等间隔平面 {"XStackedPlanes",{x1,x2,…}} 生成平面 x=xi {"CenterCutSphere",ϕopen} 正对视点处切去角 ϕopen {"CenterCutSphere",ϕopen,ϕcenter} 以 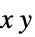 平面上的 ϕcenter 为中心角切去角 ϕopen
平面上的 ϕcenter 为中心角切去角 ϕopen - "YStackedPlanes", "ZStackedPlanes" 和 "XStackedPlanes" 的规范一样,在“范围”下面的例子中会展示更多的用法.
- 可以使用下列常见的切片表面 surfi:
-
expr0 以 x、y、z 表示的隐方程,如 x y z-10 surfaceregion 三维空间中的二维区域,如 Hyperplane volumeregion 三维空间中的三维区域,其中 surfi 为边界曲面,如 Cuboid - 可将下列封装用于切片曲面 surfi:
-
Annotation[surf,label] 提供注释 Button[surf,action] 定义当曲面被点击时应执行的操作 EventHandler[surf,…] 为曲面定义通用事件处理程序 (general event handler) Hyperlink[surf,uri] 将曲面设置为超链接 PopupWindow[surf,cont] 为曲面添加弹出窗口 StatusArea[surf,label] 当鼠标悬停在曲面处时,在状态栏中显示的内容 Tooltip[surf,label] 为曲面添加任意提示条 - SliceDensityPlot3D 与 Graphics3D 的选项相同,不同之处和更多选项如下所示: [所有选项的列表]
-
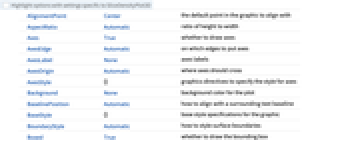
Axes True 是否绘制坐标轴 BoundaryStyle Automatic 如何设计曲面边界 BoxRatios {1,1,1} 三维边界盒的比例 ClippingStyle None 如何绘制用 PlotRange 修剪过的值 ColorFunction Automatic 如何为图上色 ColorFunctionScaling True 是否缩放传递给 ColorFunction 的参数 PerformanceGoal $PerformanceGoal 优化的目标 PlotLegends None 颜色梯度的图例 PlotPoints Automatic 每个方向上函数 f 和切片曲面 surfi 的初始样本数 PlotRange {Full,Full,Full,Automatic} 函数 f 的值域或要包括的其他值 PlotTheme $PlotTheme 绘图的整体主题 RegionFunction (True&) 如何决定是否要包括某个点 ScalingFunctions None 怎样缩放个别坐标 TargetUnits Automatic 想要使用的单位 WorkingPrecision MachinePrecision 内部计算时使用的精度 - 默认情况下,传递给 ColorFunction 的是经过缩放的 f 值.
- 默认情况下,RegionFunction 的变量由 x、y、z 和 f 提供.
- ScalingFunctions 的可能设置包括:
-
sf 缩放 f 密度值 {sx,sy,sz} 缩放 x、y 和 z 坐标轴 {sx,sy,sz,sf} 缩放 x、y 和 z 坐标轴以及 f 密度值 - 常见内置缩放函数 s 包括:
-
"Log" 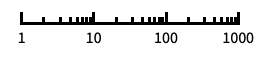
对数刻度,自动进行标记 "Log10" 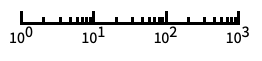
以 10 为底的对数刻度,用 10 的幂进行标记 "SignedLog" 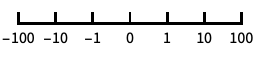
类似对数的刻度,包含 0 和负数 "Reverse" 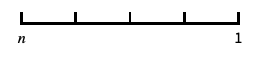
反转坐标的方向 "Infinite" 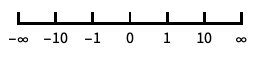
无穷刻度
所有选项的列表




范例
打开所有单元 关闭所有单元范围 (21)
曲面 (9)
在基本几何体(volume primitive)上绘制密度图相当于在 RegionBoundary[reg] 上绘制:
抽样 (3)
使用 RegionFunction 来显示被遮挡的切片:
可以用包含 Cone 的区域来指定值域:
一个含有 ImplicitRegion 的公式区域(formula region):
一个含有 BoundaryMeshRegion 的基于网格的区域:
演示 (9)
使用 PlotTheme 对整体样式进行配置:
使用 PlotLegends 显示不同数值对应的颜色:
用 Axes 控制坐标轴的显示:
可使用 AxesLabel 为坐标轴添加标签,使用 PlotLabel 为整个图添加标签:
用 ColorFunction 根据函数值为图上色:
用 BoundaryStyle 为切片曲面边界设计样式:
TargetUnits 指定在可视化图中使用哪个单位:
选项 (61)
AxesLabel (4)
ClippingStyle (2)
ColorFunction (3)
ColorFunctionScaling (2)
ImageSize (7)
PlotLegends (3)
PlotPoints (1)
使用 PlotPoints 决定切片曲面的采样:
PlotRange (3)
PlotTheme (3)
ScalingFunctions (5)
用 ScalingFunctions 缩放并反转 ![]() 轴:
轴:
TargetUnits (2)
Ticks (6)
应用 (16)
基础函数 (4)
分布函数 (5)
绘制某分布的 PDF:
绘制某分布的 CDF:
找出 MultinormalDistribution 的 Correlation 参数,其中 ρab 是 a 和 b 之间的相关系数:
可视化一个 ProductDistribution 的 PDF:
可视化某三变量数据在密度> 0.01 时的核密度估计(kernel density estimate)的 PDF:
势函数和波函数 (4)
偏微分方程 (3)
使用周期性边界条件(periodic boundary conditions)在两个空间维中可视化一个非线性的 sine-Gordon 方程,![]() 轴表示时间:
轴表示时间:
在两个空间维度中可视化 Wolfram 的非线性波动方程,![]() 轴表示时间:
轴表示时间:
可视化三维偏微分方程的解. 在此例中,为一个 Ball 上的泊松方程(Poisson equation)和狄利克雷边界条件(Dirichlet boundary conditions):
属性和关系 (5)
用 SliceContourPlot3D 在曲面上绘制等高线图:
用 ContourPlot3D 来绘制数值为常数的曲面:
用 DensityPlot3D 来呈现数值的整体可视化:
对数据使用 ListSliceDensityPlot3D:
用 DensityPlot 得到二维密度图:
相关指南
-
▪
- 函数可视化
文本
Wolfram Research (2015),SliceDensityPlot3D,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SliceDensityPlot3D.html (更新于 2022 年).
CMS
Wolfram 语言. 2015. "SliceDensityPlot3D." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/SliceDensityPlot3D.html.
APA
Wolfram 语言. (2015). SliceDensityPlot3D. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SliceDensityPlot3D.html 年
BibTeX
@misc{reference.wolfram_2025_slicedensityplot3d, author="Wolfram Research", title="{SliceDensityPlot3D}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/SliceDensityPlot3D.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_slicedensityplot3d, organization={Wolfram Research}, title={SliceDensityPlot3D}, year={2022}, url={https://reference.wolfram.com/language/ref/SliceDensityPlot3D.html}, note=[Accessed: 02-March-2026]}