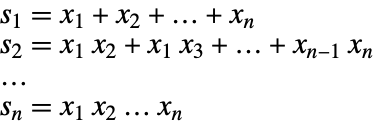代数操作

多項式の変形操作代数的数体における多項式
多項式の部分抽出三角関数式
多項式の順序複素数の変数を含む式
有理式の変形操作論理関数と区分関数
多項式の代数演算簡約化
素数を法とする多項式仮定の使用
対称式
多項式の変形操作
Expand[poly]
式の積とベキ乗を展開する
Factor[poly]
式を因数分解する
FactorTerms[poly]
数値の共通因数をくくり出す
FactorTerms[poly,{x,y,…}]
x, y, …に依存しない共通因数をくくり出す
Collect[poly,x]
多項式を x のベキ乗項として整理し直す
Collect[poly,{x,y,…}]
多項式を x, y, …のベキ乗項として整理し直す
多項式の変形操作
単一変数からなる多項式を入力する：
Expandを使い，積とベキを展開し，単純な和の形に書き直す：
Factorで多項式を完全に因数分解する：
FactorTermsを使い，多項式tのすべての項に共通な因数をカッコの外に取り出す：
同じ多項式でも，さまざまな形に書かれる．そのうちの3つの標準的な形が関数Expand，FactorTermsとFactorで得られる．Expandは，多項式の持つすべての積を展開し，式を単純な項の和の形でまとめ直す．FactorTermsは，すべての項に共通な因子でまとめ直す．また，Factorは，なるべく小さい次数の因数に分解する．
複数の変数の多項式については，変数のどれか1つを主要な変数とし，その変数について式を書き直すことが考えられる．Collect[poly,x]は，多変数の多項式を取るが，x を主変数と見立ててベキ乗項の和の形に書き直す．
2つの変数を持つ多項式を例に使う：
xを主変数とし多項式にCollectを作用させる：
主変数を複数指定した上でCollectを使う．すると，指定した変数について多項式をまとめ直してくれる：
Expand[poly,patt]
パターン patt にマッチする項を含まない部分は避けて多項式 poly を展開する
制約付きの多項式の展開
xを含まない部分は展開しないようにする：
今度は，式の部分でパターンb[_]に合ったオブジェクトを持たないものを展開から外す：
PowerExpand[expr]
式 expr に (ab)c と (ab)c の形のベキ乗項があればそれらを展開する
PowerExpand[expr,Assumptions->assum]
assum と仮定して expr を展開する
ベキと対数の展開
Wolframシステムは，cが整数である場合を除いて，(ab)cのような形の項を自動的に展開しない．一般に，後者の展開はaとbがともに正の実数であるときに限り正しい．それでも，関数PowerExpandを使えば，aとbが正の実数であると仮定し展開してくれる．
この式は自動的に展開してくれない：
それでも，PowerExpandを使うと，xとyを正の実数と仮定し展開してくれる：
Logもそのままでは展開してくれない：
今度も，PowerExpandを使えば展開できるようになる：
PowerExpandは，指定された仮定に対して正しい結果を返す：
Collect[poly,patt]
多項式においてパターン patt にマッチしたオブジェクトを共通成分とする項をまとめる
Collect[poly,patt,h]
得られた各係数部に h を適用する
式のまとめ直し
各所で関数fを使った式を入力する：
パターンf[_]にマッチするオブジェクトを共通成分とする項でまとめ直す：
求まった各項の係数部にFactorを適用する：
HornerForm[expr,x]
expr を x についてホーナー(Horner)形式にする
ホーナー形式
ホーナー形式とは，乗算の回数を最小にすることで数値をより効率よく計算できるようにする多項式の並べ方である．
以下は多項式をホーナー形式にしたものである：
多項式の部分抽出
PolynomialQ[expr,x]
式 expr が変数 x の多項式かどうか判定する
PolynomialQ[expr,{x1,x2,…}]
式 expr が変数 xi の多項式かどうか判定する
Variables[poly]
多項式 poly の持つ変数をリストアップする
Exponent[poly,x]
多項式 poly における変数 x にかかる最大指数を返す
Coefficient[poly,expr]
多項式 poly における式 expr の係数を抽出する
Coefficient[poly,expr,n]
多項式 poly における式 exprn の係数を抽出する
Coefficient[poly,expr,0]
多項式 poly において式 expr に依存しない項を抽出する
CoefficientList[poly,{x1,x2,…}]
多項式 poly の持つ xi の項の係数を抽出し配列を構成する
CoefficientRules[poly,{x1,x2,…}]
多項式の指数ベクトルと係数を抽出する
多項式の展開構造の判定と部分抽出
変数を2つ持った多項式を例に取る：
展開した形を作っておく：
PolynomialQで，式tがxの多項式か判定する．そうであることが判明する：
この式はxの多項式にはなっていない：
Variablesを使い，多項式tの持つ変数をリストアップする：
多項式tにおいてxにかかる最大指数を調べる．単一変数の多項式なら，Exponentは式の最高次数を返す：
Coefficient[poly,expr]を使い，poly で成分 expr を持つすべての項について係数を抽出する．2つ係数が見付かり，和の形で返される：
これは，Coefficient[t,x^2]に等しい：
tにおける の項から係数を抽出する：
CoefficientListを使い， の各次数における項の係数を抽出し， の係数から始まるリストを構成する：
CoefficientListを多変数の多項式に適用すると，各変数について各次数ごとに係数が抽出され，各次数ごとに配列表示される：
CoefficientRulesには，非零の係数を持つ単項式のみが含まれる：
ここで挙げた関数は，まだ展開していない多項式についても機能することが多い．
また，関数によっては，厳密な意味の多項式でなくても機能する．
a，b，cに具体的な整数値を指定しなければ，この式は厳密な意味の多項式にならない：
それでも，Exponent[expr,x]を作用させると，expr のxについて最高次数が得られる．ただし，結果は記号代数的な記述になる：
多項式の順序
多項式の主項はさまざまな方法で選ぶことができる．多変数多項式では，単項式の合計次数でソートするのが便利なことが多い．
MonomialList[poly]
単項式のリストを取得する
CoefficientRules[poly]
指数ベクトルと係数で単項式を表す
FromCoefficientRules[list]
規則のリストから多項式を構築する
多項式の異なる表現方法
次は3変数の多項式である：
これはその単項式のリストである：
下は単項式のリストを，指数ベクトルと係数で表したものである：
最初のベクトルは に対応している：
FromCoefficientRulesは，規則と変数のリストからもとの多項式を構築する：
MonomialListあるいはCoefficientRulesの第2引数が省略されている場合，変数は，関数Variablesにより返される順序で取られる．
変数のリストは常にソートされているとは限らない：
今度は最初のベクトルは に対応している：
デフォルトでは，単項式は第1変数から始まり降ベキの順という辞書式順序でソートされる．前の例では{5,4,1}（ に対応）が第2要素により{5,3,2}（に対応）に先行している．
順序は，2つの指数ベクトル，がどのようにソートされるかにより記述される．辞書式順序では次のようになる．
.
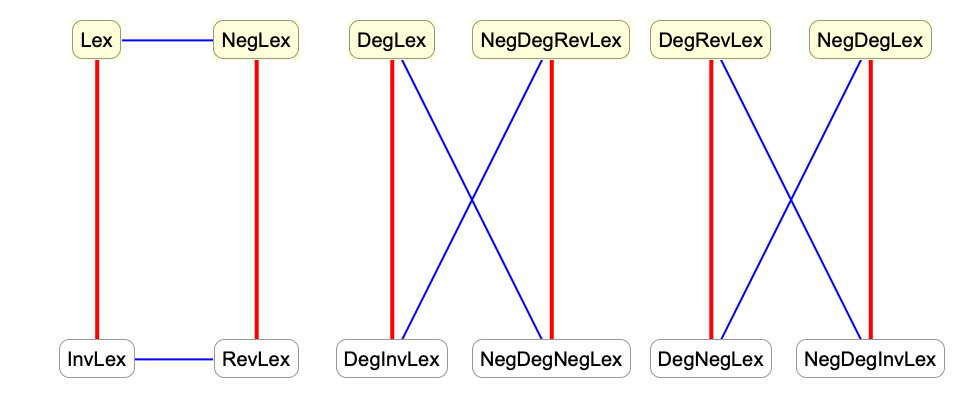
この他，順序は重み行列を与えることでも記述することができる．この場合，指数ベクトルは重み行列で乗算され，その結果が辞書式順序に降ベキの順にソートされる．異なる順序に対する行列は以下のように与えられる．

11.gif

異なる順序に対応する重み行列
GroebnerBasisとPolynomialReduceのような関数では，順序は正しく並んでいなければならない．これで要素の降順が有限（要素が非負の指数のベクトルである）ということが確実となる．このためには，重み行列の角列の非零の値は正でなければならない．
ある式の多項式項に対して使われるデフォルトのソート方法は，変数を逆の順でソートする負の辞書式順序に対応する．これは逆辞書式順序として広く知られている．
次は多項式の内部表現である．PlusとTimesの引数は評価時にソートされる：
これはソートされた項のリストである：
こては変数{x,y,z}の逆辞書式順序である：
重み行列で同じ順序を指定したものである：
結果は poly の項を自動的にソートしたリストと同一になる：
TraditionalFormでは，辞書式順序に最も近い順序で項が並べ替えられる．
TraditionalFormで表現された多項式である：
以下では高度なタイプセット機能を使い，TraditionalForm出力で現れるのと同じ順序で項のリストを得る：
結果はデフォルト（辞書式）順序で与えられる単項式のリストに一致する：
オプションParameterVariablesは，どの変数を順序から除外するかをTraditionalFormに指定する．
デフォルトでは，独立変数のリストは{a,b,x}と想定されている：
ここでxは唯一の変数であると想定される：
MonomialListで使用される6つの順序から，結果のリストを逆にするだけで別の順序が得られる．これは事実上指数ベクトルを反転させることに等しい．可換の場合は，変数の順序を反転させることによっても別の順序が得られる．
下の図はさまざまな順序間の関係を示している．赤い線は変数のリストを逆にすることを，また青い線は指数ベクトルを反転させることを意味する．
有理式の変形操作
普通の多項式では，関数FactorとExpandで式の2つの基本形が得られる．有理式になると，いろいろな形の式が役に立つ．
ExpandNumerator[expr]
分子だけを展開する
ExpandDenominator[expr]
分母だけを展開する
Expand[expr]
分子を展開した上で，各項を分母で割った形にまとめる
ExpandAll[expr]
分子と分母の両方を完全に展開し，分子の各項を分母で割った形にまとめる
有理式の展開操作のいくつか
例に使う有理式を入力する：
ExpandNumeratorを使い，各項の分子を展開する：
Expandを使うと，各項の分子を展開した上で対応する分母で割った形に式が展開される：
ExpandDenominatorだと，各項の分母が展開する：
ExpandAllを使い，各項の分子と分母の両方を展開し，分子の各項を分母で割った形にまとめる：
ExpandAll[expr,patt]
, etc.
パターン patt にマッチした項を持たない部分は展開しない
展開操作における制約の付加
zを含まない項は展開しないようにする：
Together[expr]
通分する
Apart[expr]
単純な分母を持ついくつかの分数項に展開する（部分分数分解）
Cancel[expr]
約分する
Factor[expr]
分母分子を因数分解する
有理式の構造に関する演算
例に使う有理式を入力する：
Togetherを使い，通分する：
まとめた式にFactorを適用し，分母と分子を因数分解する：
Apartを使い，より簡単な分母を持った項からなる和の式に書き直す（部分分数分解）：
Cancelを使い，分母と分子の共通因数を約分する：
Factorを使うと，まず，通分し，その後に分母分子を因数分解する：
数学用語で言えば，Apartは有理式を「部分分数」に分解することを意味する．
複数の変数を持つ式は，Apart[expr,var]を使い各変数について部分分数へ分解できる．
変数を2つ持つ有理式を作っておく：
xについて部分分数へ分解する：
今度は，yについて部分分数分解する：
多項式の代数演算
普通の計算で多項式を変形する必要があるなら，実質的に構造的操作で十分用が足りる．
しかし，さらに高等な代数計算をするなら，以下に示す機能を使う必要があるだろう．
ただし，本節で説明する演算機能のほとんどは，係数が有理数で各項の指数が整数である，通常の多項式についてのみ適用可能であるので注意しなければいけない．
PolynomialQuotient[poly1,poly2,x]
x の多項式 poly1を poly2で割ったときの商．剰余は除去する
PolynomialRemainder[poly1,poly2,x]
x の多項式 poly1を poly2で割ったときの剰余を抽出する
PolynomialQuotientRemainder[poly1,poly2,x]
商と剰余をリストで与える
PolynomialMod[poly,m]
m を法として多項式 poly を簡約する
PolynomialGCD[poly1,poly2]
2つの多項式の最大公約式を探す
PolynomialLCM[poly1,poly2]
2つの多項式の最小公倍式を探す
PolynomialExtendedGCD[poly1,poly2]
2つの多項式の拡大最小公倍式を探す
Resultant[poly1,poly2,x]
2つの多項式の終結式を返す
Subresultants[poly1,poly2,x]
2つの多項式の主部分終結式の係数を見付ける
Discriminant[poly,x]
多項式 poly の判別式を見付ける
GroebnerBasis[{poly1,poly2,…},{x1,x2,…}]
多項式 polyi についてグレブナー基底を探す
GroebnerBasis[{poly1,poly2,…},{x1,x2,…},{y1,y2,…}]
yi を消去してグレブナー基底を探す
PolynomialReduce[poly,{poly1,poly2,…},{x1,x2,…}]
多項式 poly を項 polyi で構成された最も小さい形に変換する
多項式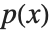の簡約化的な操作
多項式 と 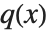が与えられたとき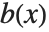，の次数が 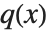より低いという条件の下で，関係式 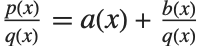は必ず一意的に決定する．商 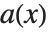はPolynomialQuotientで，また，剰余 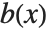はPolynomialRemainderで求めることができる．
を で割ったときの余りを求める：
今度は と の商を求め，余りは捨てる：
こうするともとの式が再構築できる：
この2つの多項式では，式がxについてのものか，yについてのものかにより答が変わってくる：
PolynomialModは，整数に対する関数Modの多項式版と考えればよい．m が整数なら，PolynomialMod[poly,m]は，単に多項式 poly の各係数を整数 m を法としてできるだけ低い次数の多項式に還元する．一方，m が多項式のときは，PolynomialMod[poly,m]は，m の適当な倍数 q m を poly から減算することで，次数を最小とした項を実効的に探そうとする．乗数 q は多項式であっても構わないが，その次数は poly の次数より低いものでなければならない．PolynomialModの返す最終的な多項式は，次数と先頭係数をともに最小化した多項式である．
を法として を簡約する．結果は単に多項式の割り算の余りである：
この場合，PolynomialModとPolynomialRemainderは同じ結果にならない：
PolynomialModとPolynomialRemainderの主な相違点は，前者が多項式の積と差を取ることで機能するのに対して，後者は割り算を用いるという点にある．また，PolynomialModは，複数の法による簡約化を可能にしている．典型的な例として，多項式と整数をともに法とする簡約化がある．
とをともに法とし を簡約する：
PolynomialGCD[poly1,poly2]は polyi を厳密に割ることのできる最高次の多項式を求める．これは整数関数GCDの多項式版と言える．
PolynomialGCDは，2つの多項式の最大公約式を与える：
PolynomialExtendedGCDは，2つの多項式の拡大最大公約式を与える：
返される多項式 および は，もとの多項式についての最大公約式を表すのに使うことができる：
関数Resultant[poly1,poly2,x]は，古典的代数問題で必要とされる各種アルゴリズムで使われる．ともに最高次の係数を1とする2つの多項式 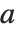と 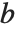の終結式は，その根の差 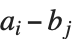の積で与えられる．ある多項式の対があるとき，それらの終結式はもとの多項式対の係数を持った多項式になることが知られている．また，終結式がゼロになるように多項式対のパラメータの値を変えることで対に共通な根を見付けることができる．最高次の係数を1とする2個の多項式は，リストSubresultants[poly1,poly2,x]の最初の 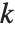個の要素がゼロであれば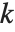， 個の共通な根を持つ．
xとyの多項式をyについて合成する．多項式に共通なyに関する根は，合成式を0にするxの値についてのみ存在する：
関数Discriminant[poly,x]はその根の差分の2乗の積である．これを使うと，その多項式に重根があるかどうかが判別できる．判別式は，変数に非依存の因数まで，多項式およびその導関数の終結式に等しい．
以下の多項式には重根があるため，判別式は消える：
以下の多項式は異なる根を持つため，その判別式は非零である：
グレブナー基底は近代代数アルゴリズムでよく使われる．関数GroebnerBasis[{poly1,poly2,…},{x1,x2,…}]は，与えられた多項式の集合を，式の性質が簡単に推定できる標準的な形に変形してくれる．また，これは重要な特徴だが， GroebnerBasisから得られる多項式系に共通な根はもとの多項式系の共通根に等しい．
は冗長なので，グレブナー基底には現れない：
多項式1は根を持たない．このため，もとの多項式には共通な根が存在しない：
求まる多項式は互いに依存しない形なので，ちょうど5つ根が存在することが分かる：
PolynomialReduce[poly,{p1,p2,…},{x1,x2,…}]はリスト形式で多項式の集合を返す．求まる多項式は， は最小次数で， は poly に等しい．
を項 と項 で書き表し，剰余は のみに依存する：
Factor[poly]
多項式を因数分解する
FactorSquareFree[poly]
多項式を無平方分解する
FactorTerms[poly,x]
x に依存しない項について因数分解する
FactorList[poly]
,
FactorSquareFreeList[poly]
,
FactorTermsList[poly]
結果の因数をリスト形式で返す
多項式の因数分解用関数
関数Factor，FactorTerms，FactorSquareFreeはさまざまの種類の多項式の因数分解を行う．Factorは，整数の範囲で因数分解を行う．FactorTermsでは，多項式の「内容」が対象になる．FactorSquareFreeでは，2乗形の因数を取り出す．
多項式を入力し，展開しておく：
FactorTermsで分解すると，xに依存しない因数2が外に引き出される：
FactorSquareFreeだと，2との因数は引き出すが，他はいじらない：
Factorを使うと，式が完全に因数分解され，もとの形が得られる：
多項式を扱うプログラムを書く場合等で，多項式の項を抽出できると後で操作するのに都合よくなることがある．関数FactorListを使うと，因数分解の後に各因数を，指数部分を付けた形で，リストの成分として得ることができる．このリストの第1要素は，必ず多項式に共通な数値形の因子がくる．
FactorListの多項式の出力の仕方は，FactorIntegerの整数の出力の仕方に相当する．
前の例で使った多項式をまた因数分解する．ただし，今度は，得られる因数をリストで出す．リストの各要素は項の因数と指数部からなる：
Factor[poly,GaussianIntegers->True]
ガウスの整数を係数に許容して因数分解する
複素数を係数に持つ因数分解
Factorとこれに関連した関数は，通常，普通の整数や有理数を係数とした多項式を扱う．GaussianIntegers->Trueのオプションを設定しておくと，Factorで実数部と虚数部がともに有理数である複素数を係数に持った多項式も扱えるようになる．普通不可能な因数分解の問題でも，この設定をしておくと可能になる場合がよくある．
普通の整数しか係数に使えないことにすると，この多項式はこれ以上因数分解できない：
ガウスの整数もよしとすると，今度は，分解可能になる：
IrreduciblePolynomialQ[poly]
poly が有理数体上の既約多項式かどうかを判定する
IrreduciblePolynomialQ[poly,GaussianIntegers->True]
poly がガウスの有理数体上で既約かどうかを判定する
IrreduciblePolynomialQ[poly,Extension->Automatic]
poly の代数的数の係数により拡張された有理数体上での既約性を判定する
既約性の判定
ある多項式が，体Fの係数を持つ2つの非定数多項式の積として表すことができない場合，その多項式は体F上で既約である．
以下の多項式は有理数体上で既約である．
ガウスの有理数体上では，可約である：
デフォルトでは，代数的数は独立変数として扱われる：
Sqrt[2]により拡張された有理数体上では，この多項式は可約である：
Cyclotomic[n,x]
n 次の x に関する円周等分多項式を構成する
円周等分多項式
円周等分した多項式は，さまざまな代数演算アルゴリズムで「基本多項式」として使われる．この多項式は，式 で定義される．ここで， は より小さく，かつ， に対して互いに素となる正整数すべてを動く．
円周等分多項式 を求める：
は の因数に現れる：
Decompose[poly,x]
可能であれば，多項式 poly をより単純な多項式の合成に分解し，それらの多項式をリストで返す
多項式の分解
因数分解は多項式の再構成に使う重要な手法の1つである．これとは異なる手法として「分解」がある．多項式 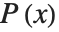を因数分解するとき，それは多項式 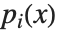の積 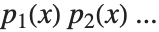の形で書かれる．一方，多項式 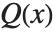を分解するときは，多項式を合成した形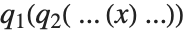，で構成されるとする．
Decomposeを使った簡単な例を見てみよう．もとの多項式 は多項式（ここで は多項式 ）と書ける：
多項式の関数を2つ作っておく：
関数を複合化した形にする：
Decomposeでもとの関数に分解する：
Decompose[poly,x]は x の多項式をリスト形式で返すが，それらの多項式を合成するともとの多項式が復元できるようになっている．このとき，もとの多項式に x 以外の変数があっても構わないがDecomposeが生成する一連の多項式は x の関数とみなされる．
因数分解と異なり，合成の仕方は完全に一意的ではない．例えば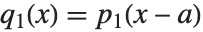，と 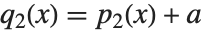の関係にある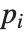多項式 と多項式 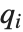は，ともに同じ合成式を与える．つまり，になる．またWolfram言語では，定数の項があれば，Decomposeの返すリストにおける最初の項に組み入れられることになっている．
InterpolatingPolynomial[{f1,f2,…},x]
x の多項式で，x が整数 i に等しいときには fi に等しくなるものを返す
InterpolatingPolynomial[{{x1,f1},{x2,f2},…},x]
x の多項式で，x が xi のときには fi に等しくなるものを返す
補間多項式を作成する
3つの点を通る二次式を求める：
xが0のとき，二次式の値は2になる：
素数を法とする多項式
素数 を法とする整数のなす有限体を とするとき，Wolfram言語は の要素を係数とする多項式も扱うことができる．
PolynomialMod[poly,p]
p を法とし多項式の係数を簡約する
Expand[poly,Modulus->p]
p を法とし poly を展開する
Factor[poly,Modulus->p]
p を法とし poly を因数分解する
PolynomialGCD[poly1,poly2,Modulus->p]
p を法とする polyi の最大公約式GCDを探す
GroebnerBasis[polys,vars,Modulus->p]
p を法とするグレブナー基底を探す
有限体上で多項式を操作するための関数
普通の多項式を例に使う：
2を法とし係数を簡約する：
得られた多項式を係数が整数の範囲で因数分解する：
2を法として計算させると，さらに因数分解を行うことが可能になる：
対称式
変数 の対称式とは， を任意に置換しても不変の多項式のことである．以下の多項式
は変数 の基本対称式と呼ばれる．
対称式の基本定理によると，， の対称式はすべて の基本対称式の多項式として表すことができる．
変数の順番が固定されているときは，任意の多項式 は， の対称部分と呼ばれる対称式 と，降順の単項式を含まない剰余 の和として表される．単項式 は であり，かつその場合に限り降順であるという．
SymmetricPolynomial[k,{x1,…,xn}]
変数 の 次基本対称式
SymmetricReduction[f,{x1,…,xn}]
となるような の多項式のペアを返す．ここで は対称部分， は剰余である
SymmetricReduction[f,{x1,…,xn},{s1,…,sn}]
の基本対称式を で置換したペアを返す
対称式計算のための関数
これは4つの変数についての三次基本対称式である：
基本対称式についての多項式を書く．入力した多項式が対称なので，剰余はゼロである：
対称部分の基本対称式が，変数 で置き換えられている．多項式は対称ではないので，剰余はゼロにならない：
SymmetricReductionは記号係数を持つ多項式に適用することができる：
代数的数体における多項式
Factorのような関数で多項式の因数分解をするとき，通常，得られる式の係数はすべてが有理数からなるものとする．ただし，オプションExtensionを設定することで係数の存在し得る領域を広げることが可能である．
Factor[poly,Extension->{a1,a2,…}]
ai の有理結合も係数に許容して多項式 poly を因数分解する
代数的数体における多項式の因数分解
係数が有理数しか取れないものとすると，この多項式は因数分解できない：
係数にを使ってもよいものとすると，因数分解ができるようになる：
係数にを使ってもよいものとしても，因数分解できる：
GaussianIntegers->Trueの条件指定はExtension->Sqrt[-1]に等しい：
との両方を使ってよいものとすれば，この多項式も完全に因数分解できる：
Expandを作用されると，もとの式が得られる：
Factor[poly,Extension->Automatic]
poly の係数が代数的数になり得るものとして，多項式 poly を因数分解する
代数的数を係数とする因数分解
係数にを持つ多項式を例に使う：
Factorのデフォルト設定だと，因数分解してくれない：
代数的数を係数に使うように指定すれば，を使い分解可能になる：
他の多項式に関する関数もFactorと同じように機能する．つまり，特に条件を指定しなければ代数的数は単なるシンボルとして扱われ，係数が有理整数において操作可能である．それに対し，Extension->Automaticとオプション設定をすれば，係数の表現に代数的数を使った変形操作が可能となる．
デフォルト設定では，これらの多項式はCancelでは約分できない：
代数的数を許すと，約分できるようになる：
デフォルト設定では，PolynomialLCMで共通な因数は見付けられない：
今度は，見付けられる：
IrreduciblePolynomialQ[poly,ExtensionAutomatic]
poly が poly の係数により拡張された有理体上の既約多項式かどうかを判定する
IrreduciblePolynomialQ[poly,Extension->{a1,a2,…}]
poly が poly の係数と a1,a2,…により拡張された有理体上で既約であるかどうかを判定する
IrreduciblePolynomialQ[poly,ExtensionAll]
すべての複素数体上での既約性を判定する
既約性の判定
ある多項式が体Fの係数を持つ2つの非定数多項式の積として表すことができない場合，その多項式はF上で既約である．
デフォルトでは，代数的数は独立変数として扱われる：
Sqrt[2]により拡張された有意数体上では，この多項式は可約である：
以下の多項式は有理数体上では既約である：
Sqrt[3]により拡張された有理数体上では，可約である：
この多項式はすべての複素数体上では既約である：
三角関数式
TrigExpand[expr]
三角関数式を項の和に展開する
TrigFactor[expr]
三角関数式を項の積に分解する
TrigFactorList[expr]
因数分解で得られる項をその指数とともにリスト形式で返す
TrigReduce[expr]
整数倍の角度を用いて三角関数式を簡約する
三角関数式の変形操作用関数
三角関数式を展開する：
展開した式を因数分解する：
得られた式を三角関数を項に使った線形な形に簡約する：
TrigExpandを使うと，双曲線関数も展開可能である：
TrigReduceでもとの形に復元する：
Wolframシステムでは，Tanのような関数が自動的に優先される：
TrigFactorListを使えば，Tanのような関数を分解した形で見ることができる：
TrigToExp[expr]
三角関数式を指数関数式に変換する
ExpToTrig[expr]
指数関数式を三角関数式に変換する
指数と三角関数の変換
TrigToExpで三角関数を指数表記に書き直す：
TrigToExpは双曲線関数に使うこともできる：
ExpToTrigで逆の変形を行う．変形操作で複素数はできる限り取り払われる：
ExpToTrigは双曲線関数や円関数にも適用できる：
ExpToTrigを純粋な数値からなる式に適用してもよい：
複素数の変数を含む式
Wolfram言語は，通常，x等の変数が実数でも複素数でも特に区別せず演算できる．それでも，変数を実数か複素数に特定した上で変換操作を行いたいときがあるだろう．
ComplexExpandは代数式や三角関数の式を展開するのに使うが，変数の取れる型は明確に条件付けられる．
ComplexExpand[expr]
すべての変数が実数であるという前提で式 expr を展開する
ComplexExpand[expr,{x1,x2,…}]
変数 xi が複素数であるという前提で式 expr を展開する
複素数からなる式の展開
xとyがともに実数であるとして，式を展開する：
この式では，aは実数である．だがxは複素数であり，展開すると実数部と虚数部に分解される：
複素変数が1つ増えただけで，展開した形は非常に複雑になる：
実数のパラメータを使い複素数の変数 z を表す方法はいくつかある．例えば，先に示したように，z は「直交座標の形式」でRe[z]+I Im[z]と書ける．また，「極形式」なら，Abs[z] Exp[I Arg[z]]と書ける．
ComplexExpandの指定にオプションTargetFunctionsの設定を付加することで，複素数の変数をどう表すべきか指定できる．TargetFunctionsには{Re,Im,Abs,Arg,Conjugate,Sign}の中の関数をリスト形式で割り付ける．すると，ComplexExpandが，与えられた関数を使い展開式の変数を書き直してくれる．何も指定していないときは， ReとImがデフォルトで使われる．
直交座標の形式で式を展開する：
今度は，極形式で展開する：
さらに，別の形式で展開してみる：
論理関数と区分関数
ネストした論理関数と区分関数は，ネストした数学関数と同じように展開することができる．展開にはLogicalExpandとPiecewiseExpandを使用する．
LogicalExpand[expr]
expr 中の論理関数を展開する
PiecewiseExpand[expr]
expr 中の区分関数を展開する
PiecewiseExpand[expr,assum]
指定の仮定のもとで展開する
論理関数と区分関数の展開
LogicalExpandは論理式をORとANDからなる標準的な選言標準形（disjunctive normal form，略してDNF）にする．
デフォルトにより，Wolfram言語はこの式を変更しない：
LogicalExpandを使うとこの式がORとANDを含む形に展開される：
LogicalExpandはすべての論理関数に使うことができ，常に論理式を標準的なORとANDの形式にする．必然的に結果が非常に大きくなることもある．
XorはANDとORを用いて表すことができる：
ネストした条件の任意の集合は常に，単一のPiecewiseオブジェクトからなる「区分標準形式」に事実上平坦化される．Wolfram言語ではPiecewiseExpandを使ってこれが行える．
デフォルトにより，Wolfram言語はこの式を変更しない：
PiecewiseExpandを使うと，この式が単一のPiecewiseオブジェクトに平坦化される：
MaxやAbsのような関数は，ClipやUnitStepと同じように，暗示的に条件を含んでいる．それらの条件の組合せはPiecewiseExpandを使って単一のPiecewiseオブジェクトに簡約することができる．
これは結果を単一のPiecewiseオブジェクトとして与える：
これは，xが実数であると仮定すると，Piecewiseオブジェクトとして書くこともできる：
Floor，Mod，FractionalPart等の関数は，原則として無限の場合を含むことができるが，Piecewiseオブジェクトによって表すこともできる．
xに境界がなければ，場合数が無限になるかもしれない：
Wolfram言語はデフォルトで，計算のどの段階においても，Floorのような単一の区分関数の展開で明示的に生成する場合数を限定している．この境界は$MaxPiecewiseCasesを再設定することで変更できる．
簡約化
Simplify[expr]
さまざまな代数的変換式と三角関数の変換式を用いて式を簡約する
FullSimplify[expr]
はるかに広い範囲の変換規則を使い簡約する
式の簡約化
Wolfram言語は，この式をそのままでは簡約してくれない：
Simplifyを適用し簡約化を強制する：
Simplifyを使えば，標準的な代数的変換式や三角関数の変換式を用いて簡約してくれる：
しかし，より高度の変換，例えば，この例にある特殊関数を含むような変換は簡約できない：
FullSimplifyを使えばさらに変換が可能である：
FullSimplify[expr,ExcludedForms->pattern]
パターン pattern にマッチする式の成分は除くようにして，式 expr を簡約する
簡約化の限定
例として，三角関数と平方根を含む式を使う：
デフォルト設定での，FullSimplifyは，式のすべてを簡約しようとする：
FullSimplifyに平方根を簡約化処理から外すように指示する：
FullSimplify[expr,TimeConstraint->t]
式 expr を簡約するが，変換処理に t 秒以上の時間がかかるようなら処理を中止する
FullSimplify[expr,TransformationFunctions->{f1,f2,…}]
式 expr の部分の変換に関数 fi だけを用いる
FullSimplify[expr,TransformationFunctions->{Automatic,f1,f2,…}]
fi と組込み変換を用いる
Simplify[expr,ComplexityFunction->c]
および
FullSimplify[expr,ComplexityFunction->c]
c を用いて最も単純な形を決定して簡約する
簡約化の限定
これは，SimplifyとFullSimplifyのどちらにも有効だが，簡約化とは，どんな式の形を使ったら最も簡単な式が形成できるかに尽きる．最適な形を自動的に探させるのではなく，意図的に指定することも可能になっている．これをするにはComplexityFunction->c のオプション設定を行う．指定した関数が候補にあがる式に適用され，最小な数値を生む候補の式が最終的な簡約した式として出力される．
Simplifyのデフォルトの設定だと，この式は何も簡約できない：
今度は，式の構成要素の個数が最小になるように簡約した形が探される：
仮定の使用
Wolfram言語は通常，オブジェクトの処理に必要なだけの最小限の仮定しかしない．これによりその結果も可能な限り一般的になる．しかし，場合によってこれらの結果は，より多くの仮定がなされた場合よりもかなり複雑になってしまうこともある．
Refine[expr,assum]
仮定を用いて expr を約す
Simplify[expr,assum]
仮定の下で簡約する
FullSimplify[expr,assum]
仮定の下で完全に簡約する
FunctionExpand[expr,assum]
仮定の下で関数を展開する
仮定の下で演算を行う
デフォルトのSimplifyはこの式に本質的には何もしない：
その理由は異なるxを選択をすると，全く異なった値になるからである：
x>0と仮定すると，Simplifyは式を直ちに0にする：
xとyについて仮定をしないと，何も実行されない：
xとyが両方とも正であると仮定された場合，対数が展開される.
SimplifyとFullSimplifyを適当な仮定の下で方程式や不等式に適用すると広範な定理を確立することもできる．
xに関する仮定を行わないと，この方程式の真偽を決定することができない：
これによりSimplifyで方程式が真であるという証明ができる：
これにより算術平均が幾何平均よりも大きいという普遍的結果が確立される：
がすべての正の引数に関して内にあるということを証明する：
SimplifyとFullSimplifyは常に式の最も簡単な形を求めようとする．しかし，場合によってはWolfram言語に特定の前提条件の下で通常の評価過程を進ませたいこともあるだろう．そのような場合にはRefineを使うとよい．Refine[expr,assum]は expr 中の変数が前提条件 assum を満たす数式で置き換えられたならばWolfram言語が自動的に行うであろう変形と同じ変形を行う．
これ以上簡単な形はSimplifyには見付けられない：
Refineは明示的な負の数xであるかのようにLog[x]を評価する：
仮定において重要なことは，あるオブジェクトが特定の領域の要素であるということを主張することである．x∈dom を用いてそのような仮定を設定することができる．ここで，∈文字はEscelEscまたは∖[Element]として入力できる．
x∈dom
または
Element[x,dom]
x は領域 dom の要素である
{x1,x2,…}∈dom
すべての xi は領域 dom の要素である
patt∈dom
patt と合致するような任意の式が領域 dom の要素である
オブジェクトは領域の要素である
が実数領域の要素であるということを確かめる：
これらの数は，すべて代数的数の要素である：
Wolfram言語は， は代数的数ではないことを知っている：
現代数学でも， が代数的数か否かまだ分かっていない：
記号xが実数領域の要素であるということを表している：
Complexes
複素数 の領域
Reals
実数 の領域
Algebraics
代数的数 の領域
Rationals
有理数 の領域
Integers
整数 の領域
Primes
素数 の領域
Booleans
ブール値（TrueおよびFalse） の領域
Wolfram言語がサポートする領域
が整数の仮定の下ではゼロである：
が実数の仮定の下での定理を確立する：
ある変数が不等式を満たしていると述べると，Wolfram言語は自動的にその変数が実数であるとみなす：
Simplify，FullSimplifyおよびFunctionExpandを仮定の下に使用することで，Wolfram言語の広大な数学的事実のコレクションにアクセスできる．
正接関数の周期性を用いる：
k/2 ∈ Integersの仮定は k が偶数である必要があるということを意味している：
Wolfram言語は，正数 に関してであることを知っている：
FullSimplifyは，特殊関数の知識にアクセスする：
Wolfram言語は，連続を扱う数学と同様に，離散数学と数論も扱える．
結果を簡約するためウィルソンの定理を用いる：
オイラーのファイ関数の乗積特性を用いる：
Simplify[expr,assum]あるいはRefine[expr,assum]のようなものには使いたい前提条件を明示的に与える．しかし，操作全体に1組の前提を指定したい場合もあるだろう．そのような場合はAssumingを使うとよい．
Assuming[assum,expr]
前提条件 assum を使って expr を評価する
$Assumptions
デフォルトの前提条件
より大きなスコープでの前提条件の指定
こうするとSimplifyがデフォルトの前提条件x>0を使う：
これは与えられた2つの前提条件を組み合せる：
SimplifyやRefineのような関数は使うべきデフォルトの前提条件を指定するオプションAssumptionsを取る．デフォルトでは，このオプションの設定はAssumptions:>$Assumptionsである．Assumingは，Blockにおけるように局所値を$Assumptionsに割り当てるという方法で作用する．
Assumptionsオプションを取るためにAssumingを使って前提条件を指定できる関数はSimplifyとRefineの他にもたくさんある．FunctionExpand，Integrate，Limit，Series，LaplaceTransform等がその例である．
Integrateでは自動的に前提条件が使われる：