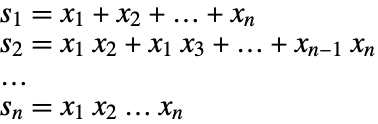代数操作

多项式的结构运算代数数域上的多项式
求多项式的结构三角函数式
多项式排序含有复变量的表达式
有理式的结构运算逻辑和分段函数
多项式的代数运算化简
对质数取模的多项式使用假设
对称多项式
多项式的结构运算
Expand[poly]
展开积和幂
Factor[poly]
完全因子分解
FactorTerms[poly]
提取数字公因子
FactorTerms[poly,{x,y,…}]
提取任何与 x、y、… 无关的公因子
Collect[poly,x]
将多项式写为 x 的幂的和
Collect[poly,{x,y,…}]
将多项式写为 x、y、… 的幂的和
多项式的结构运算.
单变量多项式：
Expand 展开乘积和幂，将多项式写为各项之和：
Factor 执行多项式的完全因子分解：
FactorTerms 提取 t 的数字公因子：
可将多项式写为多种形式. 函数 Expand、FactorTerms 和 Factor 提供了三种常见方式. Expand 将多项式写为各项之和，且展开所有的积. FactorTerms 从每项中提取公因子. Factor 进行完全因子分解，将多项式写为各项的乘积，每一项的次数都尽可能的小.
当一个多项式包含多个变量时，可以通过选择不同的变量作为“主变量”来将多项式写成不同的形式. Collect[poly,x] 接受多变量多项式，并将其重写为包含“主变量” x 的不同幂的项的和.
含有两个变量的多项式：
Collect 重写多项式，使 x 成为“主变量”：
如果指定变量列表，Collect 将表达式写成这些变量的多项式：
Expand[poly,patt]
展开 poly，避免展开不含有与 patt 匹配的项的部分
控制多项式的展开.
避免展开不含有 x 的部分：
避免展开不含有与 b[_] 匹配的对象的部分：
PowerExpand[expr]
展开 expr 中的 (ab)c 和 (ab)c
PowerExpand[expr,Assumptions->assum]
在假设条件 assum 的情况下展开 expr
展开幂和对数.
Wolfram 系统不会自动展开形式为 (ab)c 的表达式，除非 c 是整数. 通常，仅当 a 和 b 为正实数时才进行此扩展. 然而，函数 PowerExpand 可进行此扩展，实际上假定 a 和 b 确实为正实数.
Wolfram 系统不会自动展开此表达式：
PowerExpand 可进行此扩展，实际上假定 x 和 y 为正实数：
不会自动展开 Log：
PowerExpand 可进行此扩展：
PowerExpand 针对给定假设返回正确的结果：
Collect[poly,patt]
将含有与 patt 匹配的对象的项合并在一起
Collect[poly,patt,h]
对最后得到的系数应用 h
合并同类项的方法.
含有各种 f 函数的表达式：
合并与 f[_] 匹配的项：
对每个系数应用 Factor：
HornerForm[expr,x]
将 expr 写成关于 x 的霍纳形式
霍纳形式.
霍纳形式形式是一种排列多项式的方法，可通过最小化乘法次数来更有效地计算数值.
给出多项式的霍纳形式：
求多项式的结构
PolynomialQ[expr,x]
测试 expr 是否是关于 x 的多项式
PolynomialQ[expr,{x1,x2,…}]
测试 expr 是否是关于 xi 的多项式
Variables[poly]
poly 中出现的变量的列表
Exponent[poly,x]
poly 中出现的 x 的最大指数
Coefficient[poly,expr]
poly 中 expr 的系数
Coefficient[poly,expr,n]
poly 中 exprn 的系数
Coefficient[poly,expr,0]
poly 中与 expr 无关的项
CoefficientList[poly,{x1,x2,…}]
生成 poly 中 xi 的系数数组
CoefficientRules[poly,{x1,x2,…}]
获取单项式的指数向量和系数
求展开的多项式的结构.
含有两个变量的多项式：
展开的多项式：
PolynomialQ 报告 t 是关于 x 的多项式：
下面的表达式则不是关于 x 的多项式：
Variables 给出多项式 t 中出现的变量的列表：
给出多项式 t 中出现的 x 的最大指数. 对于单变量多项式，Exponent 给出多项式的次数：
Coefficient[poly,expr] poly 中 expr 的总系数. 此处，结果是两项的和：
这相当于 Coefficient[t,x^2]：
提取 t 中 的系数：
CoefficientList 给出 的各种幂的系数列表，从 的系数开始：
对于多变量多项式，CoefficientList 给出每个变量的每个幂的系数数组：
CoefficientRules 只包含具有非零系数的单项式：
重要的是要注意到，本教程中的函数也适用于未以展开形式给出的多项式.
许多函数都适用于严格意义上非多项式的表达式.
如果没有给定 a、b 和 c 特定的整数值，则严格意义上不能认为此表达式是多项式：
Exponent[expr,x] 给出 expr 中出现的 x 的最大指数，但是这里必须以符号形式给出结果：
多项式排序
可以通过许多不同的方式提取多项式的首项. 对于多变量多项式，按单项式的总次数排序通常非常有用.
MonomialList[poly]
获取单项式列表
CoefficientRules[poly]
用指数向量和系数表示单项式
FromCoefficientRules[list]
根据规则列表构建多项式
多项式的不同表示.
含有三个变量的多项式：
单项式列表：
用指数向量和系数表示的单项式列表：
第一个向量对应于 ：
FromCoefficientRules 根据规则和变量列表构建原始多项式：
如果省略了 MonomialList 或 CoefficientRules 的第二个参数，则按照函数 Variables 返回的顺序获取变量.
变量列表并不总是按顺序排列：
现在第一个向量对应于 ：
默认情况下，按字典顺序对单项式排序，以降序显示. 在上面的例子中，按第二个元素，{5,4,1}（对应于 ）排在 {5,3,2}（对应于 ）之前.
通过定义如何对两个指数向量 和 排序来描述顺序. 对于字典顺序，
.
也可以通过给出权重矩阵来描述顺序. 在这种情况下，将指数向量乘以权重矩阵，然后按字典顺序（也按降序）对结果进行排序. 不同顺序的矩阵如下所示.

11.gif

对应于不同排序的权重矩阵.
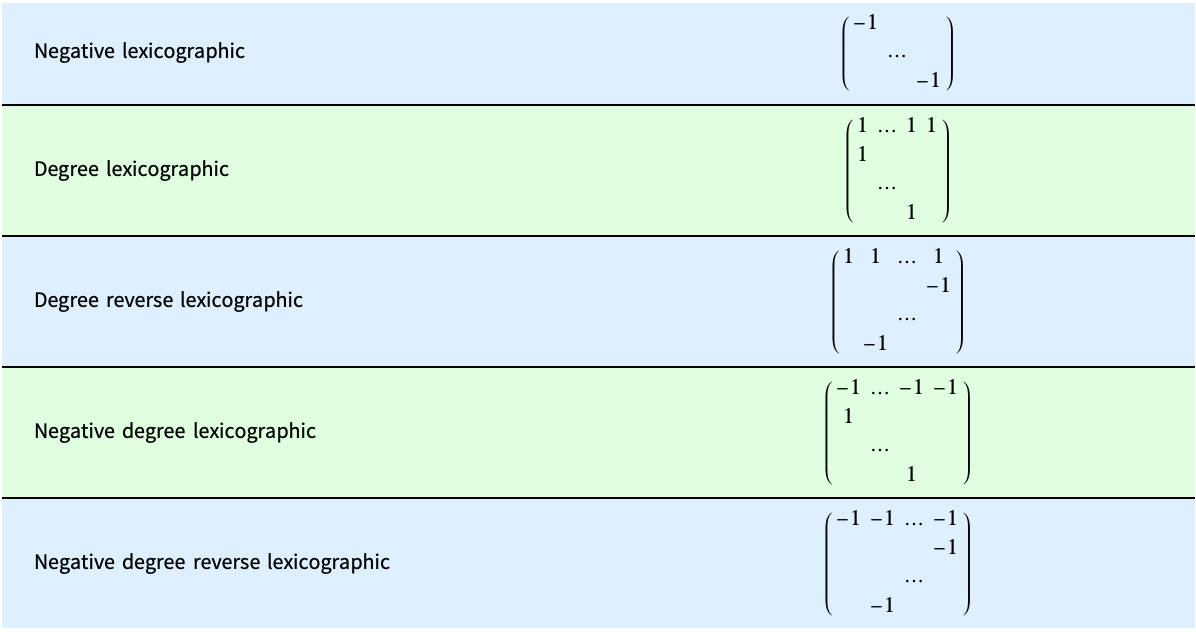
对于诸如 GroebnerBasis 和 PolynomialReduce 之类的函数，顺序必须是有理有据的，以确保元素的任何递减序列都是有限的（元素是非负指数组成的向量）. 为了使该条件成立，权重矩阵的每一列中的第一个非零值必须为正.
对表达式中多项式的默认排序对应于负字典顺序，其中以相反顺序对变量进行排序. 这通常被称为反向字典顺序.
以下是多项式的内部表示. 计算时对 Plus 和 Times 的参数进行排序：
排序后的项的列表：
按变量 {x,y,z} 的反向字典顺序排序：
这是权重矩阵指定的相同顺序：
结果与 poly 中自动排序的各项的列表相同：
TraditionalForm 尝试按接近字典顺序的顺序排列各个项.
按 TraditionalForm 显示的多项式：
下面使用高级排版功能来获取各个项的列表，顺序与在 TraditionalForm 输出中出现的顺序相同：
结果与按默认（字典）顺序给出的单项式列表一致：
选项 ParameterVariables 告诉 TraditionalForm 排序时不考虑哪些变量.
默认情况下，假定自变量列表为 {a,b,x}：
此处假定 x 是唯一的变量：
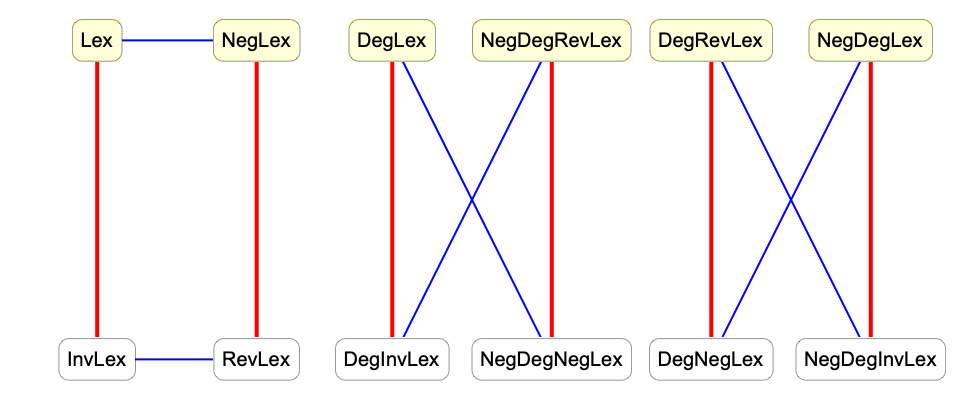
只需反转结果列表，即可从 MonomialList 中使用的六种排序中获得其他排序. 这实际上相当于对指数向量取负. 在可交换情况下，还可以通过反转变量的顺序来获得其他排序.
下图说明了各种排序之间的关系. 红线表示反转变量列表，蓝线表示对幂向量取负.
有理式的结构运算
对于普通多项式，Factor 和 Expand 给出最重要的形式. 对于有理式，有许多不同的形式都很有用.
ExpandNumerator[expr]
只展开分子
ExpandDenominator[expr]
只展开分母
Expand[expr]
展开分子，每一项都除以分母
ExpandAll[expr]
将分子和分母都全部展开
有理式的不同种类的展开式.
下面是一个有理式：
ExpandNumerator 将每一项的分子展开：
Expand 展开每一项的分子，且每一项都除以适当的分母：
ExpandDenominator 将每一项的分母展开：
ExpandAll 将每一项的分子和分母都全部展开：
ExpandAll[expr,patt]
等
避免展开不包含与 patt 匹配的项的部分
控制展开方式.
避免展开不含有 z 的项：
Together[expr]
将所有项合并在一起，放在公分母上
Apart[expr]
将表达式写成具有简单分母的项的和
Cancel[expr]
约去分子和分母的公因子
Factor[expr]
进行完全因式分解
有理式的结构运算.
下面是一个有理式：
Together 将所有项放在公分母上：
可用 Factor 对所得表达式的分子和分母进行因式分解：
Apart 将表达式写成各个项的和，每个项的分母都尽可能的简单：
Cancel 约去分子和分母的公因子：
Factor 先将所有项放在公分母上，然后对结果进行因式分解：
用数学术语来讲，Apart 将有理式分解为“部分分数”.
在含有多个变量的表达式中，可用 Apart[expr,var] 关于不同变量进行部分分数分解.
含有两个变量的有理式：
关于 x 的部分分数分解：
关于 y 的部分分数分解：
多项式的代数运算
对于许多实际计算，需要对多项式执行的唯一操作上是结构运算.
但是，如果对多项式进行更高级的代数操作，则必须使用本教程中讨论的代数运算.
需要注意的是，本教程中讨论的大多数运算仅适用于普通多项式，每一项的指数都为整数，系数皆为有理数.
PolynomialQuotient[poly1,poly2,x]
给出关于 x 的多项式 poly1 除以 poly2 的结果，丢弃余式
PolynomialRemainder[poly1,poly2,x]
给出关于 x 的多项式 poly1 除以 poly2 所得的余式
PolynomialQuotientRemainder[poly1,poly2,x]
以列表形式给出商和余式
PolynomialMod[poly,m]
对 m 取模，约简多项式 poly
PolynomialGCD[poly1,poly2]
求两个多项式的最大公因式
PolynomialLCM[poly1,poly2]
求两个多项式的最小公倍式
PolynomialExtendedGCD[poly1,poly2]
求两个多项式的扩展最大公因式
Resultant[poly1,poly2,x]
求两个多项式的结式
Subresultants[poly1,poly2,x]
求两个多项式的主子结式系数 (principal subresultant coefficient)
Discriminant[poly,x]
求多项式的 poly 的判別式
GroebnerBasis[{poly1,poly2,…},{x1,x2,…}]
求多项式 polyi 的 Gröbner 基
GroebnerBasis[{poly1,poly2,…},{x1,x2,…},{y1,y2,…}]
求消掉 yi 的 Gröbner 基
PolynomialReduce[poly,{poly1,poly2,…},{x1,x2,…}]
求用 polyi 表示时 poly 的最小表示
多项式的约简.
给定两个多项式 和 ，始终可以唯一地写出 ，其中 的次数小于 的次数. PolynomialQuotient 给出商式 ，PolynomialRemainder 给出余式 .
下面给出 除以 所得的余式：
这里是 和 的商式，舍弃余式：
返回原始表达式：
结果取决于将多项式视为关于 x 的多项式还是关于 y 的多项式：
PolynomialMod 实际上是对针对整数的函数 Mod 的模拟（针对的是多项式）. 当模 m 为整数时，PolynomialMod[poly,m] 只是将 poly 中的每个系数对整数 m 取模. 如果 m 是多项式，则 PolynomialMod[poly,m] 实际上尝试通过从 poly 中减去 m 的适当倍数 q m 来获得次数尽可能低的多项式. 倍数 q 本身可以是一个多项式，但是其次数始终小于 poly 的次数. PolynomialMod 最终给出一个多项式，其次数和首项的系数都尽可能的小.
对 取模. 结果就是除以多项式所得的余式：
此处，PolynomialMod 和 PolynomialRemainder 给出的结果不同：
PolynomialMod 和 PolynomialRemainder 之间的主要区别在于，前者只是对多项式进行相乘和相减，而后者使用除法来获取结果. 此外，PolynomialMod 允许同时对几个模式取模. 典型的情况是同时对多项式和整数取模.
同时对 和 取模：
PolynomialGCD[poly1,poly2] 给出能整除 polyi 的次数最高的多项式. 它是对整数函数 GCD 的模拟，只是针对的是多项式.
PolynomialGCD 给出了两个多项式的最大公因式：
PolynomialExtendedGCD 给出了两个多项式的扩展最大公因式：
返回的多项式 和 可用于以原始多项式表示 GCD：
函数 Resultant[poly1,poly2,x] 被用在许多经典的代数算法中. 首项系数都为 1 的两个多项式 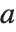和 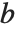的结式，由多项式所有的根之间的差 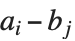的乘积给出. 事实证明，对于任何一对多项式，其结式始终两个多项式的系数所构成的多项式. 通过查看结果何时为零，可以知道两个多项式的参数取什么值时才有公根. 如果列表 Subresultants[poly1,poly2,x] 中的前 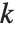个元素恰好为零，则首项系数都为 1 的两个多项式有 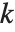个公根.
下面是含有 x 和 y 的两个多项式关于 y 的结式. 原始多项式在结式为零的 x 值处对 y 有公根：
函数 Discriminant[poly,x] 是其根的差的平方的乘积. 可用于确定多项式是否有重根. 判别式等于多项式及其导数的结式，与变量无关.
下面的多项式有重根，所以判别式为零：
下面的多项式有不同的根，所以判别式不等于零：
Gröbner 基出现在许多现代代数算法和应用中. 函数 GroebnerBasis[{poly1,poly2,…},{x1,x2,…}] 接受一组多项式，并将其简化为可以方便地推导出许多特性的标准形式. 一个重要的特点是，从 GroebnerBasis 获取的多项式组始终与原始多项式组有完全相同的公根集合.
实际上是多余的，因此不会出现在 Gröbner 基中：
多项式 1 没有根，表明原始多项式没有公根：
下面的多项式实际上已展开，现在可以看出它们有五个公根：
PolynomialReduce[poly,{p1,p2,…},{x1,x2,…}] 给出多项式列表 ，且 为最小多项式， 正好为 poly.
用 和 写出 ，其余式只依赖于 ：
Factor[poly]
对多项式进行因式分解
FactorSquareFree[poly]
将多项式写为无平方因式的乘积
FactorTerms[poly,x]
提取不依赖于 x 的项
FactorList[poly]
,
FactorSquareFreeList[poly]
,
FactorTermsList[poly]
以因式列表的形式给出结果
分解多项式的函数.
Factor、FactorTerms 和 FactorSquareFree 对多项式进行不同程度的因式分解. Factor 对整数进行完全因子分解. FactorTerms 提取多项式的“内容”. FactorSquareFree 提取出现的任何倍数因子.
以下是展开形式的多项式：
FactorTerms 提取不依赖于 x 的因子 2：
FactorSquareFree 提取出因子 2 和因式 ，但不对余下部分进行因式分解：
Factor 进行完全因式分解，恢复原始形式：
特别是当你编写处理多项式的程序时，通常会发现以标准形式提取多项式更方便. 函数 FactorList 给出了多项式的所有因子及其指数的列表. 列表的第一个元素始终是多项式的整体数值因子.
对于多项式，FactorList 返回的形式类似于由 FactorInteger 针对整数生成的形式.
下面是以上例子中多项式因子的列表. 列表的每个元素给出了因子及其指数：
Factor[poly,GaussianIntegers->True]
对多项式进行因式分解，允许用高斯整数作为系数
对系数为复数的多项式进行因式分解.
Factor 及相关函数通常只处理系数为普通整数或有理数的多项式. 但是，如果设置选项 GaussianIntegers->True，则 Factor 将允许处理系数为复数（实部和虚部为有理数）的多项式. 这使得我们可以进行更大范围的因式分解.
只允许使用普通整数时，该多项式是不可约的：
当允许使用高斯整数作为系数时，则可对多项式进行因式分解：
IrreduciblePolynomialQ[poly]
测试 poly 在有理数上是否不可约
IrreduciblePolynomialQ[poly,GaussianIntegers->True]
测试 poly 在高斯有理数上是否不可约
IrreduciblePolynomialQ[poly,Extension->Automatic]
在由 poly 的代数数系数扩展的有理数上测试不可约性
不可约性测试.
如果多项式不能表示为系数位于 F 中的两个非常数多项式的乘积，则它在数域 F 上是不可约的.
该多项式在有理数上是不可约的：
在高斯有理数上，该多项式是可约的：
默认情况下，代数数被视为自变量：
在由 Sqrt[2] 扩展的有理数上，多项式是可约的：
Cyclotomic[n,x]
给出关于 x 的 n 次分圆多项式
分圆多项式.
在各种代数算法中，分圆多项式作为“基本多项式”出现. 分圆多项式由 定义，其中 遍历所有小于 的与 互质的正整数.
分圆多项式 ：
出现在 的因式中：
Decompose[poly,x]
可能的情况下，将 poly 分解为更简单的多项式
分解多项式.
因式分解是将多项式分解为较简单部分的一种重要方法. 另一种完全不同的方法是分解. 在因式分解多项式 时，将其写为多项式 的积 . 而分解多项式 则是将其写为形为 的多项式组合.
以下是 Decompose 的一个简单例子. 原始多项式 可被写为多项式 ，其中 是多项式 ：
这里是两个多项式函数：
下面给出两个函数的复合形式：
Decompose 恢复原来的函数：
Decompose[poly,x] 被设计为给出关于 x 的多项式列表，如果重新复合这些多项式，将再现原始多项式. 原始多项式可以包含 x 以外的变量，但是 Decompose 产生的多项式序列应被视为关于 x 的函数.
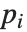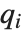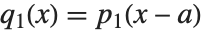与因式分解不同，多项式的分解不是完全唯一的. 例如，两组多项式 和 ， 和 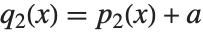给出同样的复合结果，使得 . Wolfram 语言遵循以下约定：将所有常数项吸收到 Decompose 产生的列表的第一个多项式中.
InterpolatingPolynomial[{f1,f2,…},x]
给出关于 x 的多项式，当 x 为整数 i 时，它等于 fi
InterpolatingPolynomial[{{x1,f1},{x2,f2},…},x]
给出关于 x 的多项式，当 x 为 xi 时，它等于 fi
生成插值多项式.
下面生成一个二次多项式，该二次多项式经过指定的三个点：
当 x 为 0 时，多项式的值为 2：
对质数取模的多项式
Wolfram 语言可处理系数位于有限整数域 （可对质数 取模）的多项式.
PolynomialMod[poly,p]
对 p 取模，约简多项式的系数
Expand[poly,Modulus->p]
展开 poly 模 p
Factor[poly,Modulus->p]
对 poly 模 p 进行因式分解
PolynomialGCD[poly1,poly2,Modulus->p]
求 polyi 模 p 的 GCD
GroebnerBasis[polys,vars,Modulus->p]
求模 p 的 Gröbner 基
在有限域上对多项式进行处理的函数.
这是一个普通的多项式：
对 2 取模，约简系数：
下面是所得多项式在整数上的因式：
如果对 2 取模，可进行进一步的因式分解：
对称多项式
变量 的对称多项式是在 的任意排列下不变的多项式. 多项式
被称为变量 的基本对称多项式.
对称多项式基本定理声称可用关于 的基本对称多项式表示每个关于 的对称多项式.
当变量的顺序固定时，任意多项式 可以唯一地表示为对称多项式 （称为 的对称部分）和余式 （不包含降序单项式）的和. 当且仅当 时，单项式 才被称为是降序的.
SymmetricPolynomial[k,{x1,…,xn}]
给出关于变量 的第 个基本对称多项式
SymmetricReduction[f,{x1,…,xn}]
给出关于 的一对多项式 ，使得 ，其中 是对称部分， 为余式
SymmetricReduction[f,{x1,…,xn},{s1,…,sn}]
给出一对多项式 ，将 中的基本对称多项式替换为
用于进行对称多项式计算的函数.
关于四个变量的三次基本对称多项式：
用基本对称多项式写出多项式 . 输入多项式是对称的，因此余式为零：
用变量 替换对称部分中的基本对称多项式. 多项式不是对称的，因此余式不为零：
SymmetricReduction 适用于具有符号系数的多项式：
代数数域上的多项式
像 Factor 这样的函数通常假定它们产生的多项式中的所有系数必须只含有有理数. 但是，通过设置选项 Extension，可以扩展允许的系数范围.
Factor[poly,Extension->{a1,a2,…}]
对 poly 进行因式分解，允许系数为 ai 的有理组合
在代数数域上对多项式进行因式分解.
只允许系数为有理数，因此无法对多项式进行因式分解：
如果系数可以含有 ，则可以对多项式进行因式分解：
如果系数可以含有 ，也可以对多项式进行因式分解：
GaussianIntegers->True 等价于 Extension->Sqrt[-1]：
如果系数可以同时含有 和 ，则可对多项式进行完全因式分解：
Expand 返回原始多项式：
Factor[poly,Extension->Automatic]
对 poly 进行因式分解，允许 poly 中的代数数出现在系数中
对具有代数数系数的多项式进行因式分解.
系数含有 的多项式：
默认情况下，Factor 不会对多项式进行因式分解：
但是现在，系数的数域被扩展，允许含有 ，可对多项式进行因式分解：
其他多项式函数的工作原理与 Factor 相似. 默认情况下，它们像独立符号变量一样对待代数数系数. 但如果设置了选项 Extension->Automatic，它们即可对这些系数执行运算.
默认情况下，Cancel 不对这些多项式进行约简：
但是现在可以了：
默认情况下，PolynomialLCM 无法提取公因子：
但是现在可以了：
IrreduciblePolynomialQ[poly,ExtensionAutomatic]
测试 poly 在由 poly 的系数扩展的有理数上是否不可约
IrreduciblePolynomialQ[poly,Extension->{a1,a2,…}]
测试 poly 在由 poly 的系数和 a1,a2,… 扩展的有理数上是否不可约
IrreduciblePolynomialQ[poly,ExtensionAll]
在所有复数域上测试不可约性
不可约性测试.
如果多项式不能表示为系数位于 F 中的两个非常数多项式的乘积，则它在数域 F 上是不可约的.
默认情况下，代数数被视为自变量：
在由 Sqrt[2] 扩展的有理数上，多项式是可约的：
多项式在有理数上不可约：
在由 Sqrt[3] 扩展的有理数上，多项式是可约的：
此多项式在所有复数域上都是不可约的：
三角函数式
TrigExpand[expr]
将三角函数式展开成各项的和
TrigFactor[expr]
将三角函数式分解为各项的积
TrigFactorList[expr]
用列表给出各个项及其指数
TrigReduce[expr]
用倍角约简三角函数式
用于处理三角函数式的函数.
展开三角函数式：
分解三角函数式：
将表达式简化为三角函数中的线性形式：
TrigExpand 适用于双曲函数和圆函数：
TrigReduce 恢复原始形式：
Wolfram 系统会在可能的情况下自动使用如 Tan 这样的函数：
但是，通过使用 TrigFactorList，可以看到类似于 Tan 的部分函数：
TrigToExp[expr]
用指数函数写出三角函数
ExpToTrig[expr]
用三角函数写出指数函数
与指数函数的转换.
TrigToExp 用指数函数写出三角函数：
TrigToExp 也适用于双曲函数：
ExpToTrig 进行相反的操作，在可能的情况下消除显式复数：
ExpToTrig 可处理双曲函数和圆函数：
也可以对纯数值表达式使用 ExpToTrig：
含有复变量的表达式
Wolfram 语言通常不关注 x 等变量代表实数还是复数. 但是，有时，你可能希望只有当特定变量被假定为实数或复数时才进行适当的转换.
函数 ComplexExpand 展开代数和三角函数式，对出现的变量进行确定的假设.
ComplexExpand[expr]
假定所有变量都是实数，展开 expr
ComplexExpand[expr,{x1,x2,…}]
假定 xi 为复数，展开 expr
展开复表达式.
假设 x 和 y 都是实数，展开表达式：
此处，假定 a 为实数，但假定 x 为复数，表达式被明确展开成实部和虚部：
如果有几个复变量，很快就会得到非常复杂的结果：
有几种方法可以用实参数写出复变量 z. 如上所示，z 可被写为“直角坐标形式” Re[z]+I Im[z]. 同样也可被写为“极坐标形式” Abs[z] Exp[I Arg[z]].
ComplexExpand 中的选项 TargetFunctions 允许你指定应如何写出复变量. 可以将 TargetFunctions 设为 {Re,Im,Abs,Arg,Conjugate,Sign} 中的函数. ComplexExpand 将根据要求尝试以这些形式给出结果. 默认情况下通常以 Re 和 Im 形式给出结果.
以直角坐标形式给出结果：
以极坐标形式给出结果：
另外一种形式的展开：
逻辑和分段函数
嵌套逻辑和分段函数可以像嵌套算术函数一样被展开. 可用 LogicalExpand 和 PiecewiseExpand 进行此操作.
LogicalExpand[expr]
展开 expr 中的逻辑函数
PiecewiseExpand[expr]
展开 expr 中的分段函数
PiecewiseExpand[expr,assum]
按指定假设展开表达式
展开逻辑和分段函数.
LogicalExpand 将逻辑表达式转换成标准的析取范式 (DNF)，由 ANDs 的 OR 组成.
默认情况下，Wolfram 语言保持此表达式不变：
LogicalExpand 将其展开为 ANDs 的 OR :
LogicalExpand 适用于所有逻辑函数，始终将其转换为标准的 ANDs 的 OR 形式. 有时结果会很大.
Xor 可被表示为 ANDs 的 OR：
实际上，可将任意一组嵌套条件展平为由单个 Piecewise 对象组成的分段范式 (piecewise normal form). 可以使用 PiecewiseExpand 在 Wolfram 语言中执行此操作.
默认情况下，Wolfram 语言保持此表达式不变：
PiecewiseExpand 将其展平为单个 Piecewise 对象：
如 Max 和 Abs，以及 Clip 和 UnitStep 这样的函数隐式涉及条件，通过 PiecewiseExpand 也可以将它们的组合简化为单个 Piecewise 对象.
给出单个 Piecewise对象的结果：
假设 x 为实数，也可以将下式写为 Piecewise 对象：
如 Floor、Mod 和 FractionalPart 这样的函数也可以用 Piecewise 对象来表示，尽管原则上它们可以包含无数种情况.
如果不限定 x，这将产生无数种情况：
默认情况下，Wolfram 语言限制了 Wolfram 语言在计算的任何阶段展开任何分段函数（如 Floor）时生成的分段的个数. 可以通过重置 $MaxPiecewiseCases 的值来改变此限制.
化简
Simplify[expr]
尝试各种代数和三角变换来简化表达式
FullSimplify[expr]
尝试更大范围的转换
简化表达式.
Wolfram 语言不会自动简化如下代数表达式：
Simplify 可进行简化：
Simplify 执行标准的代数和三角函数简化：
但是，它不会执行更复杂的转换，如涉及特殊函数的转换：
FullSimplify 则可以进行这样的转换：
FullSimplify[expr,ExcludedForms->pattern]
尝试化简 expr，不处理与 pattern 匹配的子表达式
控制化简.
这是一个包含三角函数和平方根的表达式：
默认情况下，FullSimplify 将尝试简化所有式子：
这将使 FullSimplify 不简化平方根：
FullSimplify[expr,TimeConstraint->t]
尝试简化 expr，每个转换最多花费 t 秒
FullSimplify[expr,TransformationFunctions->{f1,f2,…}]
只使用函数 fi 转换 expr 的构成部分
FullSimplify[expr,TransformationFunctions->{Automatic,f1,f2,…}]
使用内置转换及 fi
Simplify[expr,ComplexityFunction->c]
and
FullSimplify[expr,ComplexityFunction->c]
化简表达式，用 c 确定最简单的形式
进一步控制化简.
在 Simplify 和 FullSimplify 中始终存在一个问题，即什么才算是表达式的“最简单”形式. 可使用选项 ComplexityFunction->c 指定一个函数来确定. 该函数将被应用于表达式的每种候选形式，给出最小数值的函数将被认为是最简单的.
如果使用“简单”的默认定义，Simplify 将保持表达式不变：
现在，将试图最小化表达式中元素的数量：
使用假设
Wolfram 语言通常对你要操作的对象做出尽可能少的假设. 这意味着它给出的结果尽可能通用. 但是，如果给出更多假设，这些结果与之相比（考虑假设条件的情况下所得的结果）要复杂得多.
Refine[expr,assum]
用假设细化 expr
Simplify[expr,assum]
有假设条件的情况下进行化简
FullSimplify[expr,assum]
有假设条件的情况下进行完全化简
FunctionExpand[expr,assum]
有假设条件的情况下展开函数
有假设条件的情况下进行运算.
默认情况下，Simplify 对以下表达式不进行任何操作：
原因是如果 x 选择不同的值，其结果完全不同：
给定假设条件 x>0，Simplify 可以立即将表达式简化为 0：
如果不对 x 和 y 进行任何假设，无法执行任何操作：
如果假设 x 和 y 为正，即可展开对数：
通过对等式和不等式应用带有适当假设的 Simplify 和 FullSimplify，我们可以建立各种定理.
如果不对 x 作假设，则无法确定该等式的真伪：
Simplify 可以证明该等式是正确的：
下面确立了算术平均值大于几何平均值的标准结果：
下面证明对于所有正的参数 位于 范围内：
Simplify 和 FullSimplify 总是尝试找出表达式最简单的形式. 但是，有时你可能希望 Wolfram 语言只是遵循其普通的计算过程，但是有一些假设条件. 可以使用 Refine 来完成. 其工作原理为：如果 expr 中的变量被替换为满足假设条件 assum 的数值表达式，Refine[expr,assum] 将执行与 Wolfram 语言自动执行的转换相同的转换.
Simplify 无法找到更简单的形式：
Refine 即按 x 为负数的情况计算 Log[x]：
一类重要的假设是断言某个对象是特定域的元素. 你可以使用 x∈dom 设置此类假设，其中，可用 EscelEsc 或 ∖[Element] 来键入 ∈ 字符.
x∈dom
or
Element[x,dom]
断言 x 是域 dom 的元素
{x1,x2,…}∈dom
断言所有的 xi 是域 dom 的元素
patt∈dom
断言与 patt 匹配的任意表达式是是域 dom 的元素
断言对象是域的元素.
下面证明 是实数域的元素：
这些数字都是代数数域的元素：
Wolfram 语言知道 不是代数数：
目前数学尚不确定 是否为代数数：
下面表示断言符号 x 是实数域的元素：
Complexes
复数域
Reals
实数域
Algebraics
代数数域
Rationals
有理数域
Integers
整数域
Primes
质数域
Booleans
布尔值域（True 和 False）
Wolfram 语言支持的域.
如果假定 为整数， 为零：
如果假定 为实数，则定理 成立：
如果声称一个变量满足不等式，那么 Wolfram 语言将自动假定它是实数：
通过使用有假设条件的 Simplify、FullSimplify 和 FunctionExpand，可以访问 Wolfram 语言的大量数学内容.
使用正切线函数的周期性：
假定 k/2 ∈ Integers 意味着 k 必须是偶数：
Wolfram 语言知道对于所有正的 ，：
FullSimplify 可使用有关特殊函数的知识：
Wolfram 语言了解离散数学、数论以及连续数学.
使用威尔逊定理来简化结果：
使用 Euler phi 函数的乘性：
在如 Simplify[expr,assum] 或 Refine[expr,assum] 这样的函数中，我们可以明确给出要使用的假设. 但是有时你可能希望指定一组假设，可以在一系列操作中使用. 可通过 Assuming 来完成.
Assuming[assum,expr]
在计算 expr 时使用假设 assum
$Assumptions
默认使用的假设条件
指定更大范围的假设.
告诉 Simplify 使用默认假设 x>0:
组合使用给出的两个假设：
诸如 Simplify 和 Refine 之类的函数接受选项 Assumptions，指定了它们应使用的默认假设. 默认情况下，此选项的设置为 Assumptions:>$Assumptions. Assuming 则为 $Assumptions 分配一个本地值，就像 Block 中一样.
除了 Simplify 和 Refine，许多其他函数也接受 Assumptions 选项，因此可以通过 Assuming 为其指定假设. 举例来说，有 FunctionExpand、Integrate、Limit、Series 和 LaplaceTransform.
Integrate 中自动使用以下假设：