線形代数

行列の構築行列演算の基礎
行列の部分抽出と設定線形系の解法
スカラー，ベクトルおよび行列固有値と固有ベクトル
スカラー，ベクトルおよび行列に対する演算行列の高度な操作
ベクトルおよび行列の積テンソル
ベクトル操作疎な（スパース）配列：線形代数
逆行列
行列の構築
Table[f,{i,m},{j,n}]
i,j 番目の要素を与える i と j の関数 f を使い m×n の行列を作る
Array[f,{m,n}]
i,j 番目の要素が f[i,j]である m×n の行列を作る
ConstantArray[a,{m,n}]
すべての要素が a に等しい m×n 行列を作る
DiagonalMatrix[list]
対角成分を list とする対角行列を作る
IdentityMatrix[n]
n×n の単位行列を作る
Normal[SparseArray[{{i1,j1}->v1,{i2,j2}->v2,…},{m,n}]]
位置{ik,jk}の値 vk が非零である行列を作る
行列を作る関数
i,j 成分をa[i,j]とする2×2の行列を作る：
同じ行列を別な方法で作ってみる：
3×2の零行列を作る：
DiagonalMatrixを使うと，得られる行列で対角以外の成分はすべて0になる：
IdentityMatrix[n]を使い，n×n の単位行列を作る：
2つの非零要素を補充した3×4行列を作る：
MatrixFormは二次元形式で行列を出力する：
Table[0,{m},{n}]
零の行列
Table[If[i>=j,1,0],{i,m},{j,n}]
下三角行列
RandomReal[{0,1},{m,n}]
乱数成分を持つ行列
特殊な行列の構築
TableはIf[i≥j,a++,0]を各要素別々に評価し，下三角の部分の項目が連続的に大きくなる行列を与える：
SparseArray[{},{n,n}]
零行列
SparseArray[{i_,i_}->1,{n,n}]
n×n 単位行列
SparseArray[{i_,j_}/;i>=j->1,{n,n}]
下三角行列
SparseArrayを使って特殊な行列を構築する
これで一般的な下三角行列を設定する：
行列の部分抽出と設定
m[[i,j]]
i,j 要素を抽出する
m[[i]]
i 行目を抽出する
m[[All,i]]
i 列目を抽出する
Take[m,{i0,i1},{j0,j1}]
i0行から i1行まで，j0列から j1列までの部分行列を抽出する
m[[i0;;i1,j0;;j1]]
i0行から i1行まで，j0列から j1列までの部分行列を抽出する
m[[{i1,…,ir
}, {
j1
, … ,
js
}]]
行が ik で列が jk の要素からなる r×s の部分行列を抽出する
Tr[m,List]
対角要素を抽出する
ArrayRules[m]
非零要素の位置
行列の部分抽出法
Wolfram言語では，行列はリストのリストとして表される．したがって，Wolfram言語のリスト操作に使う標準的な演算を行列に対しても行うことができる．
3×3の行列を例に使う：
行列から第2行を抽出する：
これは行列の第2列である：
これで部分行列を抽出する：
m={{a11,a12,…},{a21,a22,…},…}
m が行列であると割り当てる
m[[i,j]]=a
要素{i,j} を a に再設定する
m[[i]]=a
行 i の全要素が a になるように再設定する
m[[i]]={a1,a2,…}
行 i の要素が{a1,a2,…}になるように再設定する
m[[i0;;i1]]={v1,v2,…}
行 i0 から i1 までがベクトル{v1,v2,…}になるように再設定する
m[[All,j]]=a
列 j の全要素が a になるように再設定する
m[[All,j]]={a1,a2,…}
列 j の要素が{a1,a2,…}になるように再設定する
m[[i0;;i1,j0;;j1]]={{a11,a12,…},{a21,a22,…},…}
行 i0から i1まで，列 j0から j1までの部分行列が新しい値となるよう再設定する
行列の部分的再設定
これは3×3行列である：
2, 2要素をxに再設定し，次いで行列全体を表示する：
今度は第2列の全要素をzに再設定する：
これは第2列の2つの要素を別々に再設定する：
第2列のすべての値を1大きくする：
指標の範囲は;; (Span)を使って指定することができる．
以下で最初の2行が新しいベクトルになるよう再設定する：
各行の第1・第3列目の要素を再設定する：
行2から3までの第1・第3列目の要素を再設定する：
スカラー，ベクトルおよび行列
行列やベクトルはリストを使って表される．リストでないものはスカラーとみなされる．
Wolfram言語では，ベクトルはスカラーのリストから構成される．また，行列はベクトルのリストから構成され，各行が個々のベクトルに対応する．正式な行列として機能するにはすべての行の長さを同じとし，矩形の配列をなすように行列の形を構成しなければならない．
VectorQ[expr]
リスト expr がベクトルを表すものかどうかを判定する（ベクトルならTrueを返し，そうでなければFalseを返す）
MatrixQ[expr]
リスト expr が行列を表すものかどうかを判定する（行列ならTrueを返し，そうでなければFalseを返す）
Dimensions[expr]
ベクトルまたは行列の次元をリスト形式で返す
ベクトルや行列の構造を判定するための関数
リスト{a,b,c}はベクトルの形式になっている：
明示的なリストでなければスカラー量とみなされる．したがって，この式にVectorQを作用させるとFalseになる：
要素の行列を構成する：
Dimensionsをベクトルに適用し，ベクトルの長さを調べる．内部でLengthが使われ長さが判明し，結果がリストとして求まる：
行の長さがちぐはぐなため，このオブジェクトは行列とはみなされない：
スカラー，ベクトルおよび行列に対する演算
Wolfram言語における数学関数のほとんどはリストの要素に個別に機能するように設定される．特に属性がListableとして与えられているものは，必ずリスト対応可能に設定される．
このためほとんどの数学関数は行列やベクトルの要素ごとに個別に機能する．
Logはベクトルの要素にそれぞれ個別に適用される：
行列についても同じことが言える．このことはネストしているすべてのリストについて当てはまる：
微分関数Dもまたリストの各要素に個別に適用される：
ベクトルの和は要素ごとに行われる：
次元の異なるベクトルの和を求めようとするとエラーになる：
スカラー1をベクトルの各要素に加える：
リストとしてとらえられないオブジェクトは，すべてスカラーとみなされる．ここでは，cがスカラーとみなされベクトルの各要素に独立して加えられる：
この場合，スカラーkがベクトルの各要素に掛け合される：
演算が終了した時点で，Wolfram言語は与えられたオブジェクトが明確なリスト形式であるもののみをベクトルとして扱う．この際，Wolfram言語はリストでないものをスカラーとみなす．すなわち，特定の演算の前後に特定の量をリストとして設定すると異なる結果となってしまう．
オブジェクトpはスカラーとして扱われる．したがって，ベクトルの各要素にそれぞれ加算される：
一方，pをリスト{c,d}として置換すると右のようになる：
一方，演算の前にpをリスト{c,d}で置換しておくとまた違った結果になる：
ベクトルおよび行列の積
cv
,
cm
等
ベクトルと行列の各要素にスカラー量を掛ける
u.v
,
v.m
,
m.v
,
m1.m2
等
ベクトルと行列の積
Cross[u,v]
ベクトルの外積（u×v としても入力可）
Outer[Times,t,u]
外積
KroneckerProduct[m1,m2,…]
クロネッカー積
ベクトルおよび行列の各種の積
スカラーkをベクトルの各要素に掛ける：
「ドット（点）」演算子は2つのベクトルのスカラー積を与える：
ドット演算子を使い行列とベクトルを掛け合せることも可能である：
ドット演算子は行列同士の積にも使う：
ドット演算子を使ったベクトルと行列の積では，右方向にでも左方向にでも積が取れる．このことは重要で，これに関連した形で，Wolfram言語では「行」ベクトルと「列」ベクトルが区別されないようになっている．Dotを使えば必要な演算操作を的確に行ってくれる（形式的には，内積 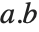とするとテンソル 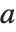の最後の添数が 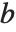の最初の添数で縮約されることを示す）．
ベクトルvと行列mを定義する：
ベクトルvにmを左側から掛け合せる．オブジェクトvが列ベクトルとして扱われることに注目：
今度は，vに右側からmを掛け合す．今度はvは行ベクトルとして扱われる：
左右両側からvをmに掛け合せる．スカラー量が得られる：
目的によっては，具体的な要素を与えずにベクトルや行列を設けたいときがある．そのようなときもDotが使え，シンボル的に積を表すことができる．
ドット演算子が非可換な積として機能する：
それでも，結合性はある：
和の内積は自動的には展開されない：
この場合，関数Distributeを使って分配則を強制できる．Distributeの使い方は「構造操作」を参照のこと：
ドット演算子は，ベクトルや行列等の「内積」を与える．高等な計算では，さらに，外積やクロネッカー(Kronecker)の積が必要になるだろう．このような演算子は一般化された関数OuterあういはKroneckerProductを使い構成できる．
ベクトルの外積は行列になる：
行列とベクトルの外積は3階のテンソルになる：
外積は「テンソル」で詳しく説明するので，そちらを参照のこと．
行列とベクトルのクロネッカー積は行列である：
1対の2×2行列のクロネッカー積は4×4の行列である：
ベクトル操作
v[[i]]
または
Part[v,i]
ベクトル v の i 番目の要素を返す
c v
ベクトル v の c 回のスカラー倍
u.v
2つのベクトルのドット積
Norm[v]
v のノルムを与える
Normalize[v]
v の方向の単位ベクトルを与える
Standardize[v]
零平均と単位標本分散を持つように v をシフトする
Standardize[v,f1]
v を f1[v]だけシフトして，単位標本分散を持つようスケールする
基本的なベクトル操作
三次元のベクトルである：
vとは逆向きで大きさが2倍のベクトルuである：
uの最初の要素がその負となるよう割り当てる：
uとvのドット積である：
vのノルムである：
vと同じ方向の単位ベクトル：
ノルムが1であることを検証する：
零平均と単位標本分散を持つように v を変換する：
以下は，変換された値は平均0と分散1を持つことを示している：
2つのベクトルのドット積がゼロであれば，そのベクトルは直交である．ベクトルの集合がすべて単位ベクトルであり，ペアで直交であるならば，その集合は直交である．
Projection[u,v]
u の v への正射影
Orthogonalize[{v1,v2,…}]
与えられたベクトルのリストから正規直交集合を生成する
直交ベクトルの操作
uのvへの投射である：
pはvのスカラー倍である：
u-pはvに対して直交である：
ベクトル集合{u,v}から開始すると，以下は2つのベクトルの正規直交集合を見付ける：
ベクトルのうちの1つが，先行するベクトルに線形依存である場合，結果において対応する位置はゼロベクトルになる：
逆行列
Inverse[m]
正方行列の逆行列を求める
逆行列
簡単な2×2の行列を入力する：
mの逆行列を求める．公式が生成される際に，行列式ad-bcがゼロではないと仮定される：
逆行列ともとの行列の積を取ると単位行列が得られるはずである：
Togetherを使い分母を約さなければ，もとの標準形単位行列が得られない：
有理数からなる行列を構成しておく：
厳密な逆行列が求まる：
もとの行列と掛け合せると単位行列が得られる：
特異行列の逆行列を求めようとすると，警告メッセージが表示され，入力したリストがそのまま返される：
文字成分からなる行列，および，厳密な数値成分からなる行列なら，Wolfram言語で厳密に逆行列を求めることが可能である．一方，行列成分の1つでも実数近似値のときは，逆行列も近似値になる．
近似実数を持つ行列を例にする：
数値計算的な逆行列を見付ける：
答をもとの行列に掛け合せると非常に小さな丸め誤差のある近似的な単位行列が得られる：
Chopを使えば，対角から外れた微小成分を削除できる：
Wolfram言語で逆行列を求めるとき，行列の成分が数値であっても厳密でありさえすれば，行列が特異かどうかが必ず判明する．一方，近似数値の行列から逆行列を求めるときは，行列が特異かどうかを確実に判明させることは困難である．判明するのは，行列式がもとの行列の成分に比べて極めて小さい，というくらいである．数値行列の逆行列を取ろうとし，それが特異であるという疑いがあるときは，Wolfram言語から警告が発せられる．
特異性の疑いがあるため，警告メッセージが表示される：
これは特異行列である．出力される警告メッセージは異なり，結果は使えない：
もとの行列で高精度の近似を使っているとき，Wolfram言語はその行列の逆行列を求めるときもその精度をなるべく保とうとする．
20桁精度の成分で6×6の行列を構成する：
もとの行列に逆行列を掛け合せ，得られる積の第1行を表示する：
20桁精度で6×6のヒルベルト(Hilbert)行列を作る．ヒルベルト行列は，数値計算的に逆にするのが難しいことで有名である：
求まる数値は正確である．ただし，精度は落ちる：
Inverseは正方行列に対してのみ機能する．「行列の高度な操作」で関数PseudoInverseを使った正方でない行列の逆行列の取り方を説明する．
行列演算の基礎
Transpose[m]
転置 m
ConjugateTranspose[m]
共役転置 m（エルミート共役）
Inverse[m]
逆行列
Det[m]
行列式
Minors[m]
小行列式
Minors[m,k]
k 番目の小行列式
Tr[m]
対角和（トレース）
MatrixRank[m]
行列の階数
行列の基本的な演算に使う関数
行列を転置すると，行と列が入れ替る．つまり，m×n の行列を転置すると n×m の行列を得ることができる．
2×3の行列を転置する．その結果，3×2の行列が求まる：
Det[m]は正方行列 m の行列式を与える．Minors[m]は第 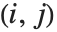要素が，m の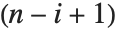第 列と第 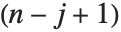行を削除することによって得られる部分行列の行列式で与えられる行列である．m の第 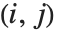余因子は，第 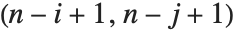要素と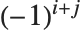 の積である．
Minors[m,k] は，m から k 個の列と k 個の行の組を可能なだけ選択することにより得られる k×k 部分行列の行列式を与える．Minorsは正方行列に加えて長方行列にも適用できることに注意する．
簡単な2×2の行列から行列式を計算する：
成分をa[i,j] とする3×3の行列を構成する：
mの行列式を求める：
行列のトレースTr[m] は，主対角要素の和である．
2×2の単純な行列のトレースが求められる：
行列の階数とは線形非依存の行または列の数である．
以下で行列の階数を求める：
MatrixPower[m,n]
n 次の行列のベキ
MatrixExp[m]
行列の指数関数
行列のベキと指数関数
2×2行列を例に見てみる：
行列 m から三次のベキを求める：
同じ行列を3回掛けたものに等しい：
行列の100万次のベキを求めてみよう：
行列 m の行列指数は である．ここで， は行列のベキを表す．
行列 m の指数関数を取る：
ベキ級数近似をもとにして m の指数関数を近似する：
線形系の解法
計算問題の多くに連立一次方程式を解く部分が含まれる．その場合，具体的に方程式を書き出して，Solveを適用するのが便利だろう．
しかし，問題の性質によっては，まず，連立一次方程式を行列の方程式の形に変換してから，行列操作の手法を使って解くこともあろう．方程式の系が一般的なアルゴリズムの一部としてあり，系がいくつ変数を持つかあらかじめ判明しないときに，このアプローチが有意義になる．
行列を使い，連立一次方程式を で表す．ここで は変数のベクトルとする．
連立一次方程式が疎，つまり行列 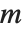のほとんどの成分がゼロであるなら，行列をSparseArrayオブジェクトとして表すのが最もよいだろう．「線形代数：疎な（スパース）配列」に説明してあるように，CoefficientArraysを使って記号方程式からSparseArrayオブジェクトに変換することができる．ここで説明してある関数はすべて通常の行列とSparseArrayオブジェクトの両方に同じように使うことができる．
LinearSolve[m,b]
行列方程式 を満足するベクトル
NullSpace[m]
行列方程式 を満足させる線形結合を持つ基底ベクトルを列挙する
MatrixRank[m]
の線形独立の行の数
RowReduce[m]
行を線形結合することで を簡約する
線形系を解き解析する
2×2の行列を構成しておく：
2つの線形方程式を作っておく：
Solveでこれらの方程式を直接解くことも可能である：
LinearSolveを使ってもベクトル解が求まる．この解はSolveで得た解に等しい：
別の解法を見てみよう．まず行列mの逆行列を取り，次に{a,b}に掛け合せる．正確だが，LinearSolveの効率には及ばない：
RowReduceには一種のガウスの消去法が使われており，この関数を使い方程式を解くことも可能である：
行列式が0でない正方行列 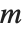から行列方程式 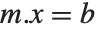を構成したとき，任意の 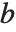に対して一意的な解が必ず存在する．一方，行列式が0の行列 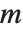の場合，任意の 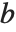に対して方程式 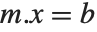を満足させるベクトル 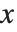は，存在しないか無限に存在するかのいずれかの状況になる．このような状態は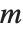， に含まれる線形方程式が独立していない場合に起る．
ただし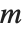， の行列式が0となる場合でも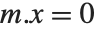， を満足させる0でないベクトル 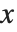は必ず存在する．この方程式を満足させるベクトルの集合 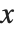は零空間，または，行列 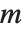の核をなすという．このベクトルはNullSpace[m]で求まる基底ベクトルの和で表すことができる．
簡単な行列を例にする．これは，2つの同じ線形方程式に対応している：
行列式は0になる：
LinearSolveでは方程式 は解けない：
mの零空間には単一基底ベクトルが存在する：
零空間の基底ベクトルにmを掛け合せると零ベクトルが得られる：
mには線形独立の行は1 行しかない：
NullSpaceとMatrixRankは特定の行列要素の組合せがゼロかどうかを決定しなければならない．近似数値行列の場合，Toleranceオプションを使ってどれくらいゼロに近ければ十分とみなし得るかを指定することができる．厳密な記号行列の場合は記号式がゼロかどうかのテストにより多くのことを行うためにZeroTest->(FullSimplify[#]==0&)のような指定が必要なこともある．
行列式が0になる，シンボルを使った簡単な行列を構成する：
mの零空間の基底には2つのベクトルがある：
mにこのベクトルの線形結合を掛けると，それがどんな組合せであってもゼロが返される：
LinearSolveやNullSpaceのような関数の重要な特徴はこれらが「正方」行列だけでなく「長方」行列にも使える点である．
線形方程式を行列方程式 で表すとき， の列数は変数の総数を表し，行数は方程式の総数を表す．連立一次方程式は次のような種類に分類できる．
劣決定系(Underdetermined)
方程式の数が変数の数より少ない．解は存在しない可能性もあれば多数存在する可能性もある
優決定系(Overdetermined)
独立方程式の数が変数の数より多い．解は存在する可能性もあれば存在しない可能性もある
非特異系(Nonsingular)
独立方程式の数が変数の数に等しく，行列式が非零．一意な解が存在する
無矛盾系(Consistent)
解は少なくとも1つ存在する
矛盾系(Inconsistent)
解は存在しない
矩形行列で表された連立一次方程式の分類
矛盾した方程式の組 と を解かせた場合どうなるか見てみる：
この行列は3つの変数からなる2つの方程式を表している：
劣決定系にLinearSolveを使う．可能な解の1つは求まる：
行列が劣決定系の方程式を表すとき，行列は自明でない零空間を持つ．この例の零空間は単一ベクトルで与えられる：
LinearSolveで求まった解に任意の零空間をなす基底ベクトルの線形合成を加えてもやはり解が得られる：
独立した方程式の数は行列MatrixRank[m]の「階数」である．重複する方程式の数はLength[NullSpace[m]]である．これらの量の合計は常に m 中の列の数に一致する．
LinearSolve[m]
という形式の方程式を解く関数を生成する
LinearSolveFunctionオブジェクトの生成
アプリケーションによっては 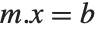という形式の方程式を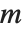， は変えずに 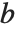だけを変化させて何度も解くことがあるだろう．Wolfram言語ではLinearSolve[m]を使っていくつのベクトルにでも適用できる単一のLinearSolveFunctionを作ることでこれを効率よく行うことができる．
これでLinearSolveFunctionを作る：
これをベクトルに適用することができる：
LinearSolveの明示的な第2引数としてベクトルを与えても同じ結果が得られる：
しかしfならいかなるベクトルにも適用できる：
LeastSquares[m,b]
最小二乗問題 を解くベクトル を与える
最小二乗問題を解く
次の線形形は矛盾を含んでいる：
LeastSquaresは を最小二乗の意味で最小にするベクトル を見付ける：
固有値と固有ベクトル
Eigenvalues[m]
m の固有値を列挙する
Eigenvectors[m]
m の固有ベクトルを列挙する
Eigensystem[m]
{eigenvalues,eigenvectors}という形式のリスト
Eigenvalues[N[m]],
等
数値的固有値
Eigenvalues[N[m,p]],
等
p 桁精度から始まる数値的な固有値
CharacteristicPolynomial[m,x]
m の特性多項式
固有値と固有ベクトル
が行列 の固有値であるとは，0以外のベクトル で となるものが存在するときをいう． を固有ベクトルと呼ぶ．
× 行列の「特性多項式」 CharacteristicPolynomial[m,x]はDet[m-x IdentityMatrix[n]]で与えられる．固有値はこの多項式の根である．
× の行列の固有値を見付けるということは，一般に 次の代数方程式を解くことを意味する．の場合，解をベキ根を使って代数的に記述することは一般に不可能である．Rootオブジェクトを使い解を構築することは可能ではあるが，ある程度疎な行列か単純な行列でないと，構築した解が複雑になりすぎて扱えなくなってしまう．
この例のような単純な行列でさえ，固有値の取る形は極めて複雑である：
Wolfram言語に近似実数を成分とする行列を与えると，近似値による固有値と固有ベクトルが算出される．
2×2の行列を例にする：
この行列はともに実数からなる固有値を2つ持つ：
mの固有ベクトルが2つ求まる：
Eigensystemを使うと固有値と固有ベクトルが同時に求まる．この割当てはvalsに固有値を割り当て，vecsに固有ベクトルを割り当てる：
第1組の固有値と固有ベクトルが適切な条件を満たしているか方程式を構成して確認する：
乱数を成分とする4×4行列の固有値を求める．非対称な行列では，固有値に虚数部が生じることがある：
関数Eigenvaluesを 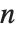× 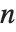行列に適用すると，固有値は 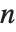個求まる．値はリスト形式で返される．固有値は行列の特性多項式の持つ根に対応するが，すべての固有値が相異なる値として求まるとは限らない．一方，Eigenvectorsを適用すると，固有ベクトルが求まり，リスト形式で返される．求まる固有ベクトルは必ず互いに独立している．求まる固有ベクトルの数が 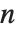に満たないとき，Eigenvectorsがリストに零ベクトルを補って，リスト長が常に になるようにする．
3×3の行列を構成する：
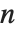0の固有値が3つ見付かる：
独立した固有ベクトルは1つしか見付からない．リスト長を3にするため，Eigenvectorsによって2つの零ベクトルが追加される：
以下は，行列の特性多項式を与える：
Eigenvalues[m,k]
m の大きい方から k 個目までの固有値
Eigenvectors[m,k]
対応する m の固有ベクトル
Eigensystem[m,k]
対応する固有ベクトルを持つ k 個の最大の固有値
Eigenvalues[m,-k]
m の小さい方から k 個目までの固有値
Eigenvectors[m,-k]
対応する m の固有ベクトル
Eigensystem[m,-k]
対応する固有ベクトルを持つ k 個の最小の固有値
最大固有値と最小固有値を求める
Eigenvaluesは数値的な固有値を絶対値の大きなものから順に並べる．行列の最大固有値あるいは最小固有値のみが知りたいことは多い．Eigenvalues[m,k]とEigenvalues[m,-k]を使うとこれが効率よく行える．
これは整数行列の厳密な固有値を計算する：
固有値は大きいものから小さいものへと並べられる：
これは絶対値が大きな方から3つ目までの固有値を与える：
Eigenvalues[{m,a}]
a についての m の一般化された固有値
Eigenvectors[{m,a}]
a についての m の一般化された固有ベクトル
Eigensystem[{m,a}]
a についての m の一般化された固有システム
CharacteristicPolynomial[{m,a},x]
a についての m の一般化された特性多項式
一般化された固有値と固有ベクトル
行列 についての行列 の一般化された固有値は である によって定義される．
一般化された固有値は一般化された特性多項式Det[m-x a]のゼロに対応する．
通常の行列の固有値は常にはっきりした値を持つが，一般化された固有値の中には一般化された特性多項式が消失してしまうと常にIndeterminateになるものもある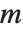． と 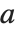が零空間を共有しているとこのようなことが起る．一般化された固有値は無限にもなり得る．
この2つの行列は一次元の零空間を共有しているので，一般化された固有値の1つはIndeterminateである：
これは，一般化された特性多項式を返す：
行列の高度な操作
SingularValueList[m]
m の非零の特異値のリスト
SingularValueList[m,k]
m の大きい方から k 番目までの特異値
SingularValueList[{m,a}]
a についての m の一般化された特異値
Norm[m,p]
m の p ノルム
Norm[m,"Frobenius"]
m のフロベニウス(Frobenius)ノルム
行列の特異値とノルムを求める
行列 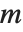の「特異値」は固有値 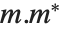の平方根である．ここではエルミート転置を表す．このような特異値の数は行列の小さい方の次元である．SingularValueListは特異値を大きいものから順に並べる．非常に小さな特異値は通常数値的に無意味である．オプション設定Tolerance->t とするとSingularValueListは最大特異値の端数 t よりも小さな特異値は除去する．近似数値行列の許容率はデフォルトでゼロよりも若干大きくなっている．
n 次元の空間における単位球内の各点のベクトルに × 行列 を掛けると 次元の楕円体が得られる．この楕円体の主軸の長さは の特異値で与えられる．
行列の「2ノルム」Norm[m,2]は楕円体の最大主軸であり，行列の最大特異値に等しい．これはまた任意の可能な単位ベクトル についての の最大の2ノルムの長さでもある．
行列の「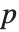 ノルム」Norm[m,p]は一般に の 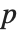ノルムの達することができる最大の長さである．最もよく考慮されているのは ，と の場合である．フロベニウスのノルムNorm[m,"Frobenius"]が考慮されることもある．これは 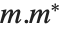のトレースの平方根である．
LUDecomposition[m]
LU分解
CholeskyDecomposition[m]
コレスキー(Cholesky)分解
正方行列の三角形への分解
LinearSolve[m]を使ってLinearSolveFunctionを作ると，これは行列 を三角形に分解することで作用する．そのような形を明示的に得られると便利なことがある．
「LU分解」は任意の正方行列を下三角行列あるいは上三角行列に効果的に分解する．「コレスキー(Cholesky)分解」は任意のエルミートの正定値行列を下三角行列とエルミート共役の積に効果的に分解する．これは行列の平方根を求めることに例えることができる．
PseudoInverse[m]
擬似逆行列
QRDecomposition[m]
QR分解
SingularValueDecomposition[m]
特異値分解
SingularValueDecomposition[{m,a}]
一般化された特異値分解
行列の直交分解
行列の逆行列の標準的な定義は，行列が正方行列あるいは特異行列ではない場合には成り立たない．しかし，行列 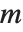の「擬似逆行列」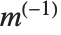はそれでも定義することができる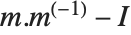． 中のすべての要素の平方の和を最小にすることで設定できる．ここで 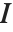は単位行列である．擬似逆行列は一般化された逆行列あるいはムーア・ペンローズ(Moore–Penrose)型の逆行列ともいわれる．これは最小二乗フィットに関連した問題で特によく使われる．
「QR分解」は任意の行列 を積 として表す．ここで は正規直交行列でありはエルミートの転置を表す．また は主対角線以下のすべての要素がゼロの三角行列である．
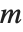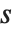「特異値分解(SVD)」は多くの数値行列のアルゴリズムの根底にある要素のひとつである．この基本概念は行列 を という形式で書き表すことで，ここで は対角線上に 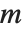の特異値を持つ行列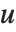， と 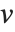は正規直交行列で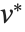， は 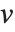のエルミート型の転置である．
JordanDecomposition[m]
ジョルダン(Jordan)分解
SchurDecomposition[m]
シューア(Schur)分解
SchurDecomposition[{m,a}]
一般化されたシューア(Schur)分解
HessenbergDecomposition[m]
ヘッセンベルク(Hessenberg)分解
固有値問題に関連する関数
ほとんどの行列は相似変換としてその固有ベクトルの行列を適用することで固有値の対角行列に約すことができる．しかし，こうするのに十分な固有ベクトルがない場合でも，行列を対角線上に固有値とジョルダン(Jordan)ブロックの両方がある「ジョルダン型」に約すことができる．「ジョルダン分解」は一般に任意の正方行列を 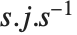として書く．
これよりも数値的により安定しているのは「シューア分解」である．これは任意の正方行列 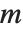を 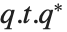として書く．ここで 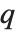は正規直交行列であり 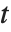はブロック上三角形である．これに関連するものとして，正方行列 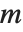を 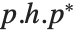の形式で表記する「ヘッセンベルク分解」が挙げられる．ここで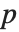， は正規直交行列であり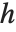， は主対角の下の対角まで非零要素を持つことができる．
テンソル
テンソルはベクトルや行列を一般化した数学的なオブジェクトである．Wolframシステムでは，テンソルはネストした多重レベルのリストで表される．リストにおける最大ネストレベルがテンソルの階数（ランク）を表す．
階数 0
スカラー
階数 1
ベクトル
階数 2
行列
階数 k
階数が k のテンソル
テンソルの階数とデータの型
k 階のテンソルは数値の k 次元の表である．リストが真の k 階テンソルになるには，その要素を k 次元の立体配列に配置することが可能でなければならない．また，立体には穴や突起があってもいけない．
テンソルの特定要素を指定する添数は立体の座標に対応している．また，テンソルの次元は立体の辺の長さに対応している．
k 階のテンソルが必要になる簡単な例に，k 個の変数に依存した関数への引数の設定がある．物理学でよく使われるテンソルでは，空間，または，時空間の持つ軸方向について添数が定義される．Wolframシステムには，共変や反変テンソルにおける添数に直接対応できる機能は組み込まれていない．そのような添数機能が必要ならば，特別に計量テンソルを使いカスタム設定する必要がある．
Table[f,{i1,n1},{i2,n2},…,{ik,nk}]
要素が f の値で与えられる n1×n2×…×nk のテンソルを作る
Array[a,{n1,n2,…,nk}]
要素が a を添数に適用することで与えられる n1×n2×…×nk のテンソルを作る
ArrayQ[t,n]
t が階数 n のテンソルかどうかテストする
Dimensions[t]
テンソルの次元を調べ，結果をリスト形式で返す
ArrayDepth[t]
テンソルの階数を求める
MatrixForm[t]
テンソル t を二次元配列に並べ替えて表示する
テンソルの作成と形状の判定
2×3×2のテンソルを入力する：
別の方法を使い同じテンソルを作成する：
MatrixFormを適用し，テンソルを二次元の配列として表示する．得られる配列は列ベクトルからなる2×3の行列として見ればよいだろう：
関数Dimensionsを使い，テンソルの次元を調べる：
テンソルの要素を抽出する：
関数ArrayDepthでテンソルの階数を調べる：
テンソルの階数は，要素を特定するのに必要な添数の数に等しい．少ない添数で要素を指定することで，部分テンソルが抽出できる．
Transpose[t]
テンソルにおいて第1，第2の添数を転置する
Transpose[t,{p1,p2,…}]
テンソルにおいて k 番目の添数が pk になるように転置する
Tr[t,f]
テンソル t の一般化された跡を構成する
Outer[f,t1,t2]
f を「積の演算子」とし，テンソル t1と t2から一般化された外積を構成する
t1.t2
テンソル t1と t2の内積を構成する（t1の最後の添数は t2の最初の添数に縮約）
Inner[f,t1,t2,g]
f を「積の演算子」，g を「和の演算子」とし，一般化された内積を構成する
テンソルの変形操作
k 階のテンソルを，添数を挿入するための「スロット」を k 個備えた入れ物ととらえると分かりやすいかもしれない．Transposeを適用させることはこれらのスロットを並べ替える作業に匹敵する．テンソルを k 次元の立方体ととらえると，Transposeの操作は立方体の回転（場合によっては，反転）と見ることができる．
Transposeの最も一般的な使い方では，テンソルの添数について任意な並べ替えが可能である．関数Transpose[T,{p1,p2,…,pk}]を適用すると，要素 T′ が要素 Tip1 ip2 … ipk で与えられる新たなテンソル T′i1 i2 … ik が求まる．
np1×np2×…×npk のテンソルにTransposeを適用させると n1×n2×…×nk のテンソルが求まる．
この行列は2×3のテンソルとも思える：
Transposeを適用すると3×2のテンソルができる．Transposeはテンソルの添数を入れる「スロット」2つを交換する，と見てもよいかもしれない：
もとのテンソルのm[[2,3]]の要素が転置されたテンソルのm[[3,2]]要素になる：
2×3×1×2のテンソルを作成する：
tの最初の2つのレベルを転置する：
答として，3×2×1×2のテンソルが求まる：
あるテンソルにおいて違ったレベルに同じリスト長のサブリストが配置されているとき，Transposeを使うことでそれらを平坦化することが可能である．
こうすると，3つのレベルすべてが平坦化される．主対角上の要素がリストに抽出される：
今度は，最初の2つのレベルだけが平坦化される：
Trを使ってテンソルの対角上の要素が抽出できる．
これは三階のテンソルの一般的な跡を構成する：
要素をリスト化した一般的な跡である：
これによって対角上の要素をレベル2まで合成する：
外積とその一般形は，低い階数のテンソルから高い階数のテンソルを構築するための方法ともとらえられる．外積は，直積やテンソル積またはクロネッカー(Kronecker)の積としても知られる．
構造的にいって，Outer[f,t,u]で構築する新たなテンソルは，テンソル t にある各要素の「位置」にテンソル u の構造を挿入した形を取る．また，新たなテンソルの各要素は，t と u の要素を f で合成することで値が決定する．
2つのベクトルから「f外積」を構成する．結果として行列ができる：
長さ3と長さ2のベクトルから「f外積」を取る．3×2の行列ができる：
2×2の行列と長さ3のベクトルから「f外積」を取る．2×2×3のテンソルができる：
テンソルの次元を調べる：
m1×m2×…×mr のテンソルと n1×n2×…×ns のテンソルについて一般化された外積を取ると，m1×…×mr×n1×…×ns のテンソルが構成される．外積を取る前のもとのテンソルの階数が r と s であれば，外積を取った結果求まるテンソルの階数は r+s になる．
添数を使い説明する．テンソル Ti1 i2 … ir と Uj1 j2 … js にOuterを適用すると，f[Ti1 i2 … ir,Uj1 j2 … js]を要素としたテンソル Vi1 i2 … irj1 j2 … js が構成される．
標準的なテンソル計算で，Outerで使う最もよく使われる関数 f は，Timesであり，それを指定することでいわゆる外積が計算できる．
特に組合せ論の問題では，f としてListがよく使われる．Outerを使うことで，ひとつのテンソルの全要素ともうひとつのテンソルの全要素から可能な限りの組合せが構築できる．
Outer[f,t,u]とすると，テンソル u がテンソル t の各要素の位置に挿入された形で新たなテンソルが構成される．また，Inner[f,t,u]でテンソルを構成すると，t の最終次元と u の第一次元を合成し，そして平坦化したような形が得られる．内積の目的は，m1×m2×…×mr のテンソルと n1×n2×…×ns のテンソルを，mr=n1としたとき，m1×m2×…×mr-1×n2×…×ns のテンソルを構成することにある．
内積の最も簡単な例としてベクトルを使った内積がある．同じベクトル長のベクトル2つにInnerを適用するとスカラーが求まる．Inner[f,v1,v2,g]とすると，普通のスカラー積を一般化した内積が構成できる．f には掛け算役の関数を指定し，g には足し算役の関数を指定しておく．
2つのベクトルの一般化した内積を取る：
これは，行列の一般化した内積：
3×2×2のテンソルを構成する：
次に2×3×1のテンソルを構成する：
3×2×3×1のテンソルを構成する：
テンソルの次元を確認する：
Innerを一方のテンソルの最終添数を他のテンソルの第1添数に「縮約」する操作と考えてもよい．他の添数のペアについて縮約をするには，まず，転置操作を行い必要な添数を第1位置と最終位置に移しておき，その後で，Innerを適用する．最後に再び転置をして添数をもとの位置に戻す．
テンソルの応用において，反対称性を実現するため符号を挿入する必要が出てくる．これは，順列の符号関数Signature[{i1,i2,…}]を使うと簡単にできる．
Outer[f,t1,t2,…]
t1,t2,…の最低レベルの要素を組み合せることで一般化された外積を構成する
Outer[f,t1,t2,…,n]
レベル n のサブリストだけを個別な要素として扱う
Outer[f,t1,t2,…,n1,n2,…]
テンソル ti におけるレベル ni のサブリストだけを個別な要素として扱う
Inner[f,t1,t2,g]
t1の最低レベルの要素を使い一般化された内積を構成す
Inner[f,t1,t2,g,n]
第1テンソルのレベル n を第2テンソルの最初のレベルで縮約する
テンソルの特定サブリストの個別扱い
すべてのシンボルが独立な要素として扱われる：
こうすると，レベル1のサブリストだけが個別要素として扱われるようになる：
ArrayFlatten[t,r]
階数 r のテンソル群の階数 r のテンソルから，平坦化された階数 r のテンソルを作る
ArrayFlatten[t]
行列の行列を平坦化する（ArrayFlatten[t,2]に等しい）
ブロックテンソルの平坦化
次はブロック行列（より大きな行列中の辺から辺までにフィットするブロックと見ることができる行列の行列）である：
次は，ブロックを貫き通して形成した行列である：
疎な（スパース）配列：線形代数
多くの大規模な線形代数アプリケーションは多くの要素を持つ行列を含んでいるが，非零要素のものは比較的少ない．WolframシステムではSparseArrayオブジェクトを使って「リストの操作：疎な（スパース）配列」で説明してあるようにこれを効果的に表現することができる．SparseArrayオブジェクトは非零の値がどこに表れるのかを指定する規則のリストを使って作用する．
SparseArray[list]
通常のリストのSparseArrayバージョン
SparseArray[{{i1,j1}->v1,{i2,j2}->v2,…},{m,n}]
要素{ik,jk}が値 vk を持つ m×n の疎な配列
SparseArray[{{i1,j1},{i2,j2},…}->{v1,v2,…},{m,n}]
同じ疎な配列
Normal[array]
SparseArrayに対応する通常のリスト
疎な配列の指定
「リストの操作：疎な（スパース）配列」で説明してあるように，パターンを使って疎な配列中の要素集団を指定することができる．また任意の階数のテンソルに対応する疎な配列を作ることもできる．
これで148個の非零要素がある50×50の疎な数値行列を作る：
これで行列要素を視覚的に表す：
これは行列中の大きい方から4番目までの固有値である：
DotはSparseArrayの結果を与える：
通常の配列と同じように部分を抽出することができる：
通常のリストに対するのと同じようにSparseArrayに対してもほとんどの標準的な構造操作を行うことができる．結果が疎である場合はSparseArrayオブジェクトが返されるのが通例である．
Dimensions[m]
配列の次元
ArrayRules[m]
配列中の非零要素の規則
m[[i,j]]
要素 i, j
m[[i]]
i 番目の行
m[[All,j]]
j 番目の列
m[[i,j]]=v
要素 i, j の再設定
SparseArrayオブジェクトに直接行える構造操作の例
これはmの第1列を与える．ここには非零要素は2つしかない：
mの第1列中の各要素に3を足す：
これで第1列の全要素が非零になった：
これは第2行の非零要素の規則を与える：
SparseArray[rules]
規則から疎な配列を生成
CoefficientArrays[{eqns1,eqns2,…},{x1,x2,…}]
方程式から係数の配列を得る
Import["file.mtx"]
ファイルから疎な配列をインポートする
疎な配列を得る典型的な方法
これは三重対角ランダム行列を生成する：
行列を10乗してもまだかなり疎である：
係数を疎な配列として抽出する：
これは対応する通常の配列である：
これでもとの形式を再生する：
CoefficientArraysは通常の整方程式を扱うことができる：
二次式部分の係数は階数3のテンソルで与えられる：
これでもとの形を再生する：
機械精度の疎な数値行列について，WolframシステムはMatrix Market形式(.mtx)やHarwell–Boeing形式のような標準的なファイル形式をサポートする．これらの形式の行列はImportやExportを用いてインポートしたりエキスポートしたりできる．