Linear Algebra
Linear Algebra
| Table[f,{i,m},{j,n}] | build an m×n matrix where f is a function of i and j that gives the value of the i,j th entry |
| Array[f,{m,n}] | build an m×n matrix whose i,j th entry is f[i,j] |
| ConstantArray[a,{m,n}] | build an m×n matrix with all entries equal to a |
| DiagonalMatrix[list] | generate a diagonal matrix with the elements of list on the diagonal |
| IdentityMatrix[n] | generate an n×n identity matrix |
| Normal[SparseArray[{{i1,j1}->v1,{i2,j2}->v2,…},{m,n}]] | make a matrix with nonzero values vk at positions {ik,jk} |
DiagonalMatrix makes a matrix with zeros everywhere except on the leading diagonal:
| Table[0,{m},{n}] | a matrix of zeros |
| Table[If[i>=j,1,0],{i,m},{j,n}] | a lower‐triangular matrix |
| RandomReal[{0,1},{m,n}] | a matrix with random numerical entries |
Table evaluates If[i≥j,a++,0] separately for each element, to give a matrix with sequentially increasing entries in the lower-triangular part:
| SparseArray[{},{n,n}] | a zero matrix |
| SparseArray[{i_,i_}->1,{n,n}] | an n×n identity matrix |
| SparseArray[{i_,j_}/;i>=j->1,{n,n}] | a lower‐triangular matrix |
Constructing special types of matrices with SparseArray.
| m[[i,j]] | the i,j th entry |
| m[[i]] | the i th row |
| m[[All,i]] | the i th column |
| Take[m,{i0,i1},{j0,j1}] | the submatrix with rows i0 through i1 and columns j0 through j1 |
| m[[i0;;i1,j0;;j1]] | the submatrix with rows i0 through i1 and columns j0 through j1 |
| m[[{i1,…,ir
}, {
j1
,
…
,
js
}]]
| the r×s submatrix with elements having row indices ik and column indices jk |
| Tr[m,List] | elements on the diagonal |
| ArrayRules[m] | positions of nonzero elements |
Matrices in the Wolfram Language are represented as lists of lists. You can use all the standard Wolfram Language list‐manipulation operations on matrices.
| m={{a11,a12,…},{a21,a22,…},…} | assign m to be a matrix |
| m[[i,j]]=a | reset element {i,j} to be a |
| m[[i]]=a | reset all elements in row i to be a |
| m[[i]]={a1,a2,…} | reset elements in row i to be {a1,a2,…} |
| m[[i0;;i1]]={v1,v2,…} | reset rows i0 through i1 to be vectors {v1,v2,…} |
| m[[All,j]]=a | reset all elements in column j to be a |
| m[[All,j]]={a1,a2,…} | reset elements in column j to be {a1,a2,…} |
| m[[i0;;i1,j0;;j1]]={{a11,a12,…},{a21,a22,…},…} | reset the submatrix with rows i0 through i1 and columns j0 through j1 to new values |
The Wolfram Language represents matrices and vectors using lists. Anything that is not a list the Wolfram Language considers as a scalar.
A vector in the Wolfram Language consists of a list of scalars. A matrix consists of a list of vectors, representing each of its rows. In order to be a valid matrix, all the rows must be the same length, so that the elements of the matrix effectively form a rectangular array.
| VectorQ[expr] | |
| MatrixQ[expr] | |
| Dimensions[expr] | a list of the dimensions of a vector or matrix |
Most mathematical functions in the Wolfram Language are set up to apply themselves separately to each element in a list. This is true in particular of all functions that carry the attribute Listable.
A consequence is that most mathematical functions are applied element by element to matrices and vectors.
The Log applies itself separately to each element in the vector:
The differentiation function D also applies separately to each element in a list:
Any object that is not manifestly a list is treated as a scalar. Here c is treated as a scalar, and added separately to each element in the vector:
It is important to realize that the Wolfram Language treats an object as a vector in a particular operation only if the object is explicitly a list at the time when the operation is done. If the object is not explicitly a list, the Wolfram Language always treats it as a scalar. This means that you can get different results, depending on whether you assign a particular object to be a list before or after you do a particular operation.
You would have gotten a different result if you had replaced p by {c,d} before you did the first operation:
| cv
,
cm
, etc.
| multiply each element by a scalar |
| u.v
,
v.m
,
m.v
,
m1.m2
, etc.
| vector and matrix multiplication |
| Cross[u,v] |
vector cross product (also input as
u×v
)
|
| Outer[Times,t,u] | outer product |
| KroneckerProduct[m1,m2,…] | Kronecker product |
It is important to realize that you can use "dot" for both left‐ and right‐multiplication of vectors by matrices. The Wolfram Language makes no distinction between "row" and "column" vectors. Dot carries out whatever operation is possible. (In formal terms, 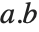 contracts the last index of the tensor
contracts the last index of the tensor 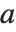 with the first index of
with the first index of 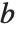 .)
.)
This left‐multiplies the vector v by m. The object v is effectively treated as a column vector in this case:
For some purposes, you may need to represent vectors and matrices symbolically without explicitly giving their elements. You can use Dot to represent multiplication of such symbolic objects.
You can apply the distributive law in this case using the function Distribute, as discussed in "Structural Operations":
The "dot" operator gives "inner products" of vectors, matrices, and so on. In more advanced calculations, you may also need to construct outer or Kronecker products of vectors and matrices. You can use the general function Outer or KroneckerProduct to do this.
Outer products are discussed in more detail in "Tensors".
| v[[i]] or Part[v,i] | give the i th element in the vector v |
| c v | scalar multiplication of c times the vector v |
| u.v | dot product of two vectors |
| Norm[v] | give the norm of v |
| Normalize[v] | give a unit vector in the direction of v |
| Standardize[v] | shift v to have zero mean and unit sample variance |
| Standardize[v,f1] | shift v by f1[v] and scale to have unit sample variance |
Two vectors are orthogonal if their dot product is zero. A set of vectors is orthonormal if they are all unit vectors and are pairwise orthogonal.
| Projection[u,v] | give the orthogonal projection of u onto v |
| Orthogonalize[{v1,v2,…}] | generate an orthonormal set from the given list of vectors |
When one of the vectors is linearly dependent on the vectors preceding it, the corresponding position in the result will be a zero vector:
| Inverse[m] | find the inverse of a square matrix |
This gives the inverse of m. In producing this formula, the Wolfram Language implicitly assumes that the determinant ad-bc is nonzero:
You have to use Together to clear the denominators, and get back a standard identity matrix:
If you try to invert a singular matrix, the Wolfram Language prints a warning message, and returns the input unchanged:
If you give a matrix with exact symbolic or numerical entries, the Wolfram Language gives the exact inverse. If, on the other hand, some of the entries in your matrix are approximate real numbers, then the Wolfram Language finds an approximate numerical result.
When you try to invert a matrix with exact numerical entries, the Wolfram Language can always tell whether or not the matrix is singular. When you invert an approximate numerical matrix, The Wolfram Language can usually not tell for certain whether or not the matrix is singular: all it can tell is, for example, that the determinant is small compared to the entries of the matrix. When the Wolfram Language suspects that you are trying to invert a singular numerical matrix, it prints a warning.
The Wolfram Language prints a warning if you invert a numerical matrix that it suspects is singular:
If you work with high‐precision approximate numbers, the Wolfram Language will keep track of the precision of matrix inverses that you generate.
This generates a 20‐digit numerical approximation to a 6×6 Hilbert matrix. Hilbert matrices are notoriously hard to invert numerically:
Inverse works only on square matrices. "Advanced Matrix Operations" discusses the function PseudoInverse, which can also be used with nonsquare matrices.
| Transpose[m] | transpose m |
| ConjugateTranspose[m] | conjugate transpose m (Hermitian conjugate) |
| Inverse[m] | matrix inverse |
| Det[m] | determinant |
| Minors[m] | matrix of minors |
| Minors[m,k] | k th minors |
| Tr[m] | trace |
| MatrixRank[m] | rank of matrix |
Transposing a matrix interchanges the rows and columns in the matrix. If you transpose an m×n matrix, you get an n×m matrix as the result.
Det[m] gives the determinant of a square matrix m. Minors[m] is the matrix whose 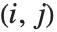 th element gives the determinant of the submatrix obtained by deleting the
th element gives the determinant of the submatrix obtained by deleting the 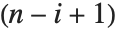 th row and the
th row and the 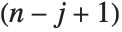 th column of m. The
th column of m. The 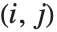 th cofactor of m is
th cofactor of m is 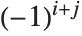 times the
times the 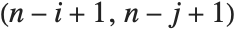 th element of the matrix of minors.
th element of the matrix of minors.
Minors[m,k] gives the determinants of the k×k submatrices obtained by picking each possible set of k rows and k columns from m. Note that you can apply Minors to rectangular, as well as square, matrices.
The trace or spur of a matrix Tr[m] is the sum of the terms on the leading diagonal.
| MatrixPower[m,n] | n th matrix power |
| MatrixExp[m] | matrix exponential |
Many calculations involve solving systems of linear equations. In many cases, you will find it convenient to write down the equations explicitly, and then solve them using Solve.
In some cases, however, you may prefer to convert the system of linear equations into a matrix equation, and then apply matrix manipulation operations to solve it. This approach is often useful when the system of equations arises as part of a general algorithm, and you do not know in advance how many variables will be involved.
Note that if your system of equations is sparse, so that most of the entries in the matrix 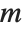 are zero, then it is best to represent the matrix as a SparseArray object. As discussed in "Sparse Arrays: Linear Algebra", you can convert from symbolic equations to SparseArray objects using CoefficientArrays. All the functions described here work on SparseArray objects as well as ordinary matrices.
are zero, then it is best to represent the matrix as a SparseArray object. As discussed in "Sparse Arrays: Linear Algebra", you can convert from symbolic equations to SparseArray objects using CoefficientArrays. All the functions described here work on SparseArray objects as well as ordinary matrices.
| LinearSolve[m,b] | a vector |
| NullSpace[m] | a list of linearly independent vectors whose linear combinations span all solutions to the matrix equation |
| MatrixRank[m] | the number of linearly independent rows or columns of |
| RowReduce[m] | a simplified form of |
You can use Solve directly to solve these equations:
You can also get the vector of solutions by calling LinearSolve. The result is equivalent to the one you get from Solve:
Another way to solve the equations is to invert the matrix m, and then multiply {a,b} by the inverse. This is not as efficient as using LinearSolve:
RowReduce performs a version of Gaussian elimination and can also be used to solve the equations:
If you have a square matrix 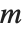 with a nonzero determinant, then you can always find a unique solution to the matrix equation
with a nonzero determinant, then you can always find a unique solution to the matrix equation 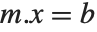 for any
for any 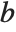 . If, however, the matrix
. If, however, the matrix 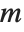 has determinant zero, then there may be either no vector, or an infinite number of vectors
has determinant zero, then there may be either no vector, or an infinite number of vectors 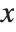 which satisfy
which satisfy 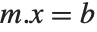 for a particular
for a particular 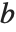 . This occurs when the linear equations embodied in
. This occurs when the linear equations embodied in 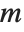 are not independent.
are not independent.
When 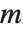 has determinant zero, it is nevertheless always possible to find nonzero vectors
has determinant zero, it is nevertheless always possible to find nonzero vectors 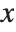 that satisfy
that satisfy 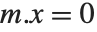 . The set of vectors
. The set of vectors 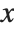 satisfying this equation form the null space or kernel of the matrix
satisfying this equation form the null space or kernel of the matrix 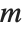 . Any of these vectors can be expressed as a linear combination of a particular set of basis vectors, which can be obtained using NullSpace[m].
. Any of these vectors can be expressed as a linear combination of a particular set of basis vectors, which can be obtained using NullSpace[m].
NullSpace and MatrixRank have to determine whether particular combinations of matrix elements are zero. For approximate numerical matrices, the Tolerance option can be used to specify how close to zero is considered good enough. For exact symbolic matrices, you may sometimes need to specify something like ZeroTest->(FullSimplify[#]==0&) to force more to be done to test whether symbolic expressions are zero.
An important feature of functions like LinearSolve and NullSpace is that they work with rectangular, as well as square, matrices.
When you represent a system of linear equations by a matrix equation of the form 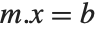 , the number of columns in
, the number of columns in 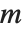 gives the number of variables, and the number of rows gives the number of equations. There are a number of cases.
gives the number of variables, and the number of rows gives the number of equations. There are a number of cases.
Underdetermined | number of equations less than the number of variables; no solutions or many solutions may exist |
Overdetermined | number of independent equations more than the number of variables; solutions may or may not exist |
Nonsingular |
number of independent equations equal to the number of variables, and determinant nonzero; a unique solution exists
|
Consistent | at least one solution exists |
Inconsistent | no solutions exist |
LinearSolve gives one of the possible solutions to this underdetermined set of equations:
When a matrix represents an underdetermined system of equations, the matrix has a nontrivial null space. In this case, the null space is spanned by a single vector:
If you take the solution you get from LinearSolve, and add any linear combination of the basis vectors for the null space, you still get a solution:
The number of independent equations is the rank of the matrix MatrixRank[m]. The number of redundant equations is Length[NullSpace[m]]. Note that the sum of these quantities is always equal to the number of columns in m.
| LinearSolve[m] | generate a function for solving equations of the form |
Generating LinearSolveFunction objects.
In some applications, you will want to solve equations of the form 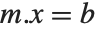 many times with the same
many times with the same 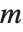 , but different
, but different 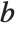 . You can do this efficiently in the Wolfram Language by using LinearSolve[m] to create a single LinearSolveFunction that you can apply to as many vectors as you want.
. You can do this efficiently in the Wolfram Language by using LinearSolve[m] to create a single LinearSolveFunction that you can apply to as many vectors as you want.
This creates a LinearSolveFunction:
You get the same result by giving the vector as an explicit second argument to LinearSolve:
| LeastSquares[m,b] | give a vector |
| Eigenvalues[m] | a list of the eigenvalues of m |
| Eigenvectors[m] | a list of the eigenvectors of m |
| Eigensystem[m] | a list of the form {eigenvalues,eigenvectors} |
| Eigenvalues[N[m]], etc. | numerical eigenvalues |
| Eigenvalues[N[m,p]], etc. | numerical eigenvalues, starting with p‐digit precision |
| CharacteristicPolynomial[m,x] | the characteristic polynomial of m |
The eigenvalues of a matrix 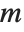 are the values
are the values 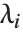 for which one can find nonzero vectors
for which one can find nonzero vectors 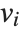 such that
such that  . The eigenvectors are the vectors
. The eigenvectors are the vectors 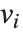 .
.
The characteristic polynomial CharacteristicPolynomial[m,x] for an 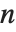 ×
×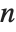 matrix is given by Det[m-x IdentityMatrix[n]]. The eigenvalues are the roots of this polynomial.
matrix is given by Det[m-x IdentityMatrix[n]]. The eigenvalues are the roots of this polynomial.
Finding the eigenvalues of an 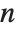 ×
×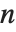 matrix in general involves solving an
matrix in general involves solving an 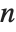 th‐degree polynomial equation. For
th‐degree polynomial equation. For  , therefore, the results cannot in general be expressed purely in terms of explicit radicals. Root objects can nevertheless always be used, although except for fairly sparse or otherwise simple matrices the expressions obtained are often unmanageably complex.
, therefore, the results cannot in general be expressed purely in terms of explicit radicals. Root objects can nevertheless always be used, although except for fairly sparse or otherwise simple matrices the expressions obtained are often unmanageably complex.
If you give a matrix of approximate real numbers, the Wolfram Language will find the approximate numerical eigenvalues and eigenvectors.
Eigensystem computes the eigenvalues and eigenvectors at the same time. The assignment sets vals to the list of eigenvalues, and vecs to the list of eigenvectors:
This finds the eigenvalues of a random 4×4 matrix. For nonsymmetric matrices, the eigenvalues can have imaginary parts:
The function Eigenvalues always gives you a list of 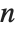 eigenvalues for an
eigenvalues for an 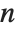 ×
×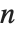 matrix. The eigenvalues correspond to the roots of the characteristic polynomial for the matrix, and may not necessarily be distinct. Eigenvectors, on the other hand, gives a list of eigenvectors which are guaranteed to be independent. If the number of such eigenvectors is less than
matrix. The eigenvalues correspond to the roots of the characteristic polynomial for the matrix, and may not necessarily be distinct. Eigenvectors, on the other hand, gives a list of eigenvectors which are guaranteed to be independent. If the number of such eigenvectors is less than 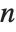 , then Eigenvectors supplements the list with zero vectors, so that the total length of the list is always
, then Eigenvectors supplements the list with zero vectors, so that the total length of the list is always 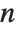 .
.
There is, however, only one independent eigenvector for the matrix. Eigenvectors appends two zero vectors to give a total of three vectors in this case:
| Eigenvalues[m,k] | the largest k eigenvalues of m |
| Eigenvectors[m,k] | the corresponding eigenvectors of m |
| Eigensystem[m,k] | the largest k eigenvalues with corresponding eigenvectors |
| Eigenvalues[m,-k] | the smallest k eigenvalues of m |
| Eigenvectors[m,-k] | the corresponding eigenvectors of m |
| Eigensystem[m,-k] | the smallest k eigenvalues with corresponding eigenvectors |
Eigenvalues sorts numeric eigenvalues so that the ones with large absolute value come first. In many situations, you may be interested only in the largest or smallest eigenvalues of a matrix. You can get these efficiently using Eigenvalues[m,k] and Eigenvalues[m,-k].
| Eigenvalues[{m,a}] | the generalized eigenvalues of m with respect to a |
| Eigenvectors[{m,a}] | the generalized eigenvectors of m with respect to a |
| Eigensystem[{m,a}] | the generalized eigensystem of m with respect to a |
| CharacteristicPolynomial[{m,a},x] | the generalized characteristic polynomial of m with respect to a |
The generalized eigenvalues for a matrix 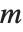 with respect to a matrix
with respect to a matrix 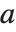 are defined to be those
are defined to be those 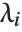 for which
for which 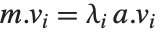 .
.
The generalized eigenvalues correspond to zeros of the generalized characteristic polynomial Det[m-x a].
Note that while ordinary matrix eigenvalues always have definite values, some generalized eigenvalues will always be Indeterminate if the generalized characteristic polynomial vanishes, which happens if 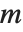 and
and 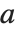 share a null space. Note also that generalized eigenvalues can be infinite.
share a null space. Note also that generalized eigenvalues can be infinite.
These two matrices share a one‐dimensional null space, so one generalized eigenvalue is Indeterminate:
| SingularValueList[m] | the list of nonzero singular values of m |
| SingularValueList[m,k] | the k largest singular values of m |
| SingularValueList[{m,a}] | the generalized singular values of m with respect to a |
| Norm[m,p] | the p‐norm of m |
| Norm[m,"Frobenius"] | the Frobenius norm of m |
The singular values of a matrix 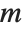 are the square roots of the eigenvalues of
are the square roots of the eigenvalues of 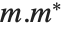 , where
, where  denotes Hermitian transpose. The number of such singular values is the smaller dimension of the matrix. SingularValueList sorts the singular values from largest to smallest. Very small singular values are usually numerically meaningless. With the option setting Tolerance->t, SingularValueList drops singular values that are less than a fraction t of the largest singular value. For approximate numerical matrices, the tolerance is by default slightly greater than zero.
denotes Hermitian transpose. The number of such singular values is the smaller dimension of the matrix. SingularValueList sorts the singular values from largest to smallest. Very small singular values are usually numerically meaningless. With the option setting Tolerance->t, SingularValueList drops singular values that are less than a fraction t of the largest singular value. For approximate numerical matrices, the tolerance is by default slightly greater than zero.
If you multiply the vector for each point in a unit sphere in 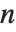 ‐dimensional space by an
‐dimensional space by an 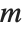 ×
×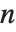 matrix
matrix 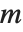 , then you get an
, then you get an 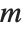 ‐dimensional ellipsoid, whose principal axes have lengths given by the singular values of
‐dimensional ellipsoid, whose principal axes have lengths given by the singular values of 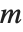 .
.
The 2‐norm of a matrix Norm[m,2] is the largest principal axis of the ellipsoid, equal to the largest singular value of the matrix. This is also the maximum 2‐norm length of 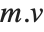 for any possible unit vector
for any possible unit vector 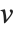 .
.
The 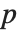 ‐norm of a matrix Norm[m,p] is in general the maximum
‐norm of a matrix Norm[m,p] is in general the maximum 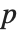 ‐norm length of
‐norm length of  that can be attained. The cases most often considered are
that can be attained. The cases most often considered are  ,
,  , and
, and  . Also sometimes considered is the Frobenius norm Norm[m,"Frobenius"], which is the square root of the trace of
. Also sometimes considered is the Frobenius norm Norm[m,"Frobenius"], which is the square root of the trace of 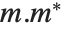 .
.
| LUDecomposition[m] | the LU decomposition |
| CholeskyDecomposition[m] | the Cholesky decomposition |
When you create a LinearSolveFunction using LinearSolve[m], this often works by decomposing the matrix 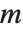 into triangular forms, and sometimes it is useful to be able to get such forms explicitly.
into triangular forms, and sometimes it is useful to be able to get such forms explicitly.
LU decomposition effectively factors any square matrix into a product of lower‐ and upper‐triangular matrices. Cholesky decomposition effectively factors any Hermitian positive‐definite matrix into a product of a lower‐triangular matrix and its Hermitian conjugate, which can be viewed as the analog of finding a square root of a matrix.
| PseudoInverse[m] | the pseudoinverse |
| QRDecomposition[m] | the QR decomposition |
| SingularValueDecomposition[m] | the singular value decomposition |
| SingularValueDecomposition[{m,a}] | the generalized singular value decomposition |
The standard definition for the inverse of a matrix fails if the matrix is not square or is singular. The pseudoinverse 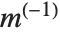 of a matrix
of a matrix 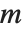 can however still be defined. It is set up to minimize the sum of the squares of all entries in
can however still be defined. It is set up to minimize the sum of the squares of all entries in 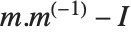 , where
, where 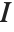 is the identity matrix. The pseudoinverse is sometimes known as the generalized inverse, or the Moore–Penrose inverse. It is particularly used for problems related to least‐squares fitting.
is the identity matrix. The pseudoinverse is sometimes known as the generalized inverse, or the Moore–Penrose inverse. It is particularly used for problems related to least‐squares fitting.
QR decomposition writes any matrix 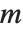 as a product
as a product 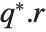 , where
, where 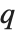 is an orthonormal matrix,
is an orthonormal matrix,  denotes Hermitian transpose, and
denotes Hermitian transpose, and 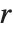 is a triangular matrix, in which all entries below the leading diagonal are zero.
is a triangular matrix, in which all entries below the leading diagonal are zero.
Singular value decomposition, or SVD, is an underlying element in many numerical matrix algorithms. The basic idea is to write any matrix 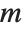 in the form
in the form  , where
, where 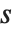 is a matrix with the singular values of
is a matrix with the singular values of 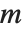 on its diagonal,
on its diagonal, 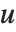 and
and 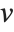 are orthonormal matrices, and
are orthonormal matrices, and 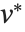 is the Hermitian transpose of
is the Hermitian transpose of 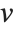 .
.
| JordanDecomposition[m] | the Jordan decomposition |
| SchurDecomposition[m] | the Schur decomposition |
| SchurDecomposition[{m,a}] | the generalized Schur decomposition |
| HessenbergDecomposition[m] | the Hessenberg decomposition |
Most square matrices can be reduced to a diagonal matrix of eigenvalues by applying a matrix of their eigenvectors as a similarity transformation. But even when there are not enough eigenvectors to do this, one can still reduce a matrix to a Jordan form in which there are both eigenvalues and Jordan blocks on the diagonal. Jordan decomposition in general writes any square matrix in the form as 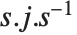 .
.
Numerically more stable is the Schur decomposition, which writes any square matrix 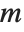 in the form
in the form 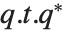 , where
, where 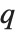 is an orthonormal matrix, and
is an orthonormal matrix, and 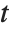 is block upper‐triangular. Also related is the Hessenberg decomposition, which writes a square matrix
is block upper‐triangular. Also related is the Hessenberg decomposition, which writes a square matrix 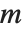 in the form
in the form 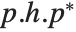 , where
, where 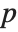 is an orthonormal matrix, and
is an orthonormal matrix, and 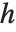 can have nonzero elements down to the diagonal below the leading diagonal.
can have nonzero elements down to the diagonal below the leading diagonal.
Tensors are mathematical objects that give generalizations of vectors and matrices. In the Wolfram System, a tensor is represented as a set of lists, nested to a certain number of levels. The nesting level is the rank of the tensor.
A tensor of rank k is essentially a k‐dimensional table of values. To be a true rank k tensor, it must be possible to arrange the elements in the table in a k‐dimensional cuboidal array. There can be no holes or protrusions in the cuboid.
The indices that specify a particular element in the tensor correspond to the coordinates in the cuboid. The dimensions of the tensor correspond to the side lengths of the cuboid.
One simple way that a rank k tensor can arise is in giving a table of values for a function of k variables. In physics, the tensors that occur typically have indices which run over the possible directions in space or spacetime. Notice, however, that there is no built‐in notion of covariant and contravariant tensor indices in the Wolfram System: you have to set these up explicitly using metric tensors.
| Table[f,{i1,n1},{i2,n2},…,{ik,nk}] | |
create an n1×n2×…×nk tensor whose elements are the values of f | |
| Array[a,{n1,n2,…,nk}] | create an n1×n2×…×nk tensor with elements given by applying a to each set of indices |
| ArrayQ[t,n] | test whether t is a tensor of rank n |
| Dimensions[t] | give a list of the dimensions of a tensor |
| ArrayDepth[t] | find the rank of a tensor |
| MatrixForm[t] | print with the elements of t arranged in a two‐dimensional array |
MatrixForm displays the elements of the tensor in a two‐dimensional array. You can think of the array as being a 2×3 matrix of column vectors:
Dimensions gives the dimensions of the tensor:
ArrayDepth gives the rank of the tensor:
The rank of a tensor is equal to the number of indices needed to specify each element. You can pick out subtensors by using a smaller number of indices.
| Transpose[t] | transpose the first two indices in a tensor |
| Transpose[t,{p1,p2,…}] | transpose the indices in a tensor so that the k th becomes the pk th |
| Tr[t,f] | form the generalized trace of the tensor t |
| Outer[f,t1,t2] | form the generalized outer product of the tensors t1 and t2 with "multiplication operator" f |
| t1.t2 | form the dot product of t1 and t2 (last index of t1 contracted with first index of t2) |
| Inner[f,t1,t2,g] | form the generalized inner product, with "multiplication operator" f and "addition operator" g |
You can think of a rank k tensor as having k "slots" into which you insert indices. Applying Transpose is effectively a way of reordering these slots. If you think of the elements of a tensor as forming a k‐dimensional cuboid, you can view Transpose as effectively rotating (and possibly reflecting) the cuboid.
In the most general case, Transpose allows you to specify an arbitrary reordering to apply to the indices of a tensor. The function Transpose[T,{p1,p2,…,pk}] gives you a new tensor T′ such that the value of T′i1 i2 … ik is given by Tip1 ip2 … ipk.
If you originally had an np1×np2×…×npk tensor, then by applying Transpose, you will get an n1×n2×…×nk tensor.
Applying Transpose gives you a 3×2 tensor. Transpose effectively interchanges the two "slots" for tensor indices:
If you have a tensor that contains lists of the same length at different levels, then you can use Transpose to effectively collapse different levels.
You can also use Tr to extract diagonal elements of a tensor.
Outer products, and their generalizations, are a way of building higher‐rank tensors from lower‐rank ones. Outer products are also sometimes known as direct, tensor, or Kronecker products.
From a structural point of view, the tensor you get from Outer[f,t,u] has a copy of the structure of u inserted at the "position" of each element in t. The elements in the resulting structure are obtained by combining elements of t and u using the function f.
If you take the generalized outer product of an m1×m2×…×mr tensor and an n1×n2×…×ns tensor, you get an m1×…×mr×n1×…×ns tensor. If the original tensors have ranks r and s, your result will be a rank r+s tensor.
In terms of indices, the result of applying Outer to two tensors Ti1 i2 … ir and Uj1 j2 … js is the tensor Vi1 i2 … irj1 j2 … js with elements f[Ti1 i2 … ir,Uj1 j2 … js].
In doing standard tensor calculations, the most common function f to use in Outer is Times, corresponding to the standard outer product.
Particularly in doing combinatorial calculations, however, it is often convenient to take f to be List. Using Outer, you can then get combinations of all possible elements in one tensor, with all possible elements in the other.
In constructing Outer[f,t,u] you effectively insert a copy of u at every point in t. To form Inner[f,t,u], you effectively combine and collapse the last dimension of t and the first dimension of u. The idea is to take an m1×m2×…×mr tensor and an n1×n2×…×ns tensor, with mr=n1, and get an m1×m2×…×mr-1×n2×…×ns tensor as the result.
The simplest examples are with vectors. If you apply Inner to two vectors of equal length, you get a scalar. Inner[f,v1,v2,g] gives a generalization of the usual scalar product, with f playing the role of multiplication, and g playing the role of addition.
You can think of Inner as performing a "contraction" of the last index of one tensor with the first index of another. If you want to perform contractions across other pairs of indices, you can do so by first transposing the appropriate indices into the first or last position, then applying Inner, and then transposing the result back.
In many applications of tensors, you need to insert signs to implement antisymmetry. The function Signature[{i1,i2,…}], which gives the signature of a permutation, is often useful for this purpose.
| Outer[f,t1,t2,…] | form a generalized outer product by combining the lowest‐level elements of t1,t2,… |
| Outer[f,t1,t2,…,n] | treat only sublists at level n as separate elements |
| Outer[f,t1,t2,…,n1,n2,…] | treat only sublists at level ni in ti as separate elements |
| Inner[f,t1,t2,g] | form a generalized inner product using the lowest‐level elements of t1 |
| Inner[f,t1,t2,g,n] | contract index n of the first tensor with the first index of the second tensor |
| ArrayFlatten[t,r] | create a flat rank r tensor from a rank r tensor of rank r tensors |
| ArrayFlatten[t] |
Here is a block matrix (a matrix of matrices that can be viewed as blocks that fit edge to edge within a larger matrix):
Many large-scale applications of linear algebra involve matrices that have many elements, but comparatively few that are nonzero. You can represent such sparse matrices efficiently in the Wolfram System using SparseArray objects, as discussed in "Sparse Arrays: Manipulating Lists". SparseArray objects work by having lists of rules that specify where nonzero values appear.
| SparseArray[list] | a SparseArray version of an ordinary list |
| SparseArray[{{i1,j1}->v1,{i2,j2}->v2,…},{m,n}] | |
an m×n sparse array with element {ik,jk} having value vk | |
| SparseArray[{{i1,j1},{i2,j2},…}->{v1,v2,…},{m,n}] | |
the same sparse array | |
| Normal[array] | the ordinary list corresponding to a SparseArray |
As discussed in "Sparse Arrays: Manipulating Lists", you can use patterns to specify collections of elements in sparse arrays. You can also have sparse arrays that correspond to tensors of any rank.
You can apply most standard structural operations directly to SparseArray objects, just as you would to ordinary lists. When the results are sparse, they typically return SparseArray objects.
| Dimensions[m] | the dimensions of an array |
| ArrayRules[m] | the rules for nonzero elements in an array |
| m[[i,j]] | element i, j |
| m[[i]] | the i th row |
| m[[All,j]] | the j th column |
| m[[i,j]]=v | reset element i, j |
A few structural operations that can be done directly on SparseArray objects.
| SparseArray[rules] | generate a sparse array from rules |
| CoefficientArrays[{eqns1,eqns2,…},{x1,x2,…}] | |
get arrays of coefficients from equations | |
| Import["file.mtx"] | import a sparse array from a file |
CoefficientArrays can handle general polynomial equations: