FourierTransform

FourierTransform[expr,t,ω]

gives the symbolic Fourier transform of expr.

FourierTransform[expr,{t1,t2,…},{ω1,ω2,…}]

gives the multidimensional Fourier transform of expr.

Details and Options

  • The Fourier transform and its inverse are a way to transform between the time domain and the frequency domain.
  • Fourier transforms are typically used to reduce ordinary and partial differential equations to algebraic or ordinary differential equations, respectively. They are also used extensively in control theory and signal processing. Finally, they have applications in studying quantum mechanical phenomena, noise filtering, etc.
  • The Fourier transform of the time domain function 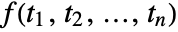is the frequency domain function :
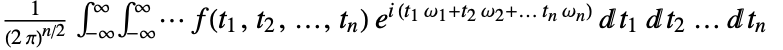  • The Fourier transform of a function is by default defined to be .
  • The multidimensional Fourier transform of a function is by default defined to be or when using vector notation .
  • Different choices of definitions can be specified using the option FourierParameters.
  • The integral is computed using numerical methods if the third argument, , is given a numerical value.
  • The asymptotic Fourier transform can be computed using Asymptotic.
  • There are several related Fourier transformations:
  • FourierTransforminfinite continuous-time functions (FT)
    FourierSequenceTransforminfinite discrete-time functions (DTFT)
    FourierCoefficientfinite continuous-time functions (FS)
    Fourierfinite discrete-time functions (DFT)
  • The Fourier transform is an automorphism in the Schwartz vector space of functions whose derivatives are rapidly decreasing and thus induces an automorphism in its dual: the space of tempered distributions. These include absolutely integrable functions, well-behaved functions of polynomial growth and compactly supported distributions.
  • Hence, FourierTransform not only works with absolutely integrable functions, but it can also handle a variety of tempered distributions such as DiracDelta to enlarge the pool of functions or generalized functions it can effectively transform.
  • The following options can be given:
  • AccuracyGoal Automaticdigits of absolute accuracy sought
    Assumptions $Assumptionsassumptions to make about parameters
    FourierParameters {0,1}parameters to define the Fourier transform
    GenerateConditions Falsewhether to generate answers that involve conditions on parameters
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoal Automaticdigits of precision sought
    WorkingPrecision Automaticthe precision used in internal computations
  • Common settings for FourierParameters include:
  • {0,1}default setting/physics
    {1,-1}systems engineering/mathematics
    {-1,1}classical physics
    {0,-2Pi}ordinary frequency
    {a,b}general setting
  • In TraditionalForm, FourierTransform is output using ℱ. »

Examples

open allclose all

Basic Examples  (6)

Compute the Fourier transform of a function:

Plot the function and its Fourier transform:

Fourier transform of :

For the systems engineering convention, change the parameters:

The Fourier transform of a Gaussian is another Gaussian:

Plot both Gaussians:

Compute the Fourier transform of a multivariate function:

Plot the result:

Compute the transform at a single point:

Scope  (44)

Basic Uses  (4)

Fourier transform of a function for a symbolic parameter :

Fourier transforms of trigonometric functions:

Evaluate the Fourier transform for a numerical value of the parameter :

TraditionalForm formatting:

Elementary Functions  (8)

Fourier transform of a power function:

Polynomial:

Fourier transform of rational functions:

Plot the transform:

Plot the real and imaginary parts:

Reciprocal of square root:

Plot the transform:

Expressions involving trigonometric functions:

Ratio of sine and linear function:

Plot the transform:

Composition of elementary functions:

Plot the transform:

Logarithmic function:

Plot the transform:

Special Functions  (5)

Sinc function:

Plot the transform:

Expressions involving Bessel functions:

Plot the transform:

SinIntegral function:

Laguerre polynomial:

Airy function:

Plot the magnitude of the Fourier transform for complex :

Piecewise Functions and Distributions  (7)

Fourier transform of a piecewise function:

Absolute value using Sign function:

Restriction of a sine function to a half-period:

Triangular function:

Ramp:

UnitStep:

Product of UnitStep and cosine functions:

Plot the magnitude and phase:

Periodic Functions  (5)

Fourier transform of SquareWave:

TriangleWave:

SawtoothWave:

Full-wave-rectified function with period :

Rectified wave:

Generalized Functions  (5)

Fourier transform involving HeavisideTheta:

Plot the magnitude and phase:

DiracDelta:

Derivative of DiracDelta:

HeavisideLambda:

HeavisidePi:

Multivariate Functions  (5)

Bivariate Fourier transform of a constant:

Exponential function:

Trivariate cosine:

Product of power and exponential:

Fourier transform of a product of exponential and SquareWave functions:

Formal Properties  (3)

Fourier transform of a first-order derivative:

Fourier transform of a second-order derivative:

Fourier transform threads itself over equations:

Numerical Evaluation  (2)

Calculate the Fourier transform at a single point:

Alternatively, calculate the Fourier transform symbolically:

Then evaluate it for the specific value of :

Options  (7)

AccuracyGoal  (1)

The option AccuracyGoal sets the number of digits of accuracy:

With default settings:

Assumptions  (1)

Specify the range of a variable using Assumptions:

FourierParameters  (2)

Fourier transform for the unit box function and different parameters:

Set up your particular global choice of parameters to work with ordinary frequency once per session:

Restore defaults:

GenerateConditions  (1)

Use GenerateConditionsTrue to get parameter conditions for when a result is valid:

PrecisionGoal  (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision  (1)

If WorkingPrecision is specified, the computation is done at that working precision:

With default settings:

Applications  (11)

Signals and Systems  (3)

Find the convolution of signals:

The product of their Fourier transforms:

Find the inverse transform:

Compare with Convolve:

Spectrum of the product of two signals, with one given in the frequency domain by:

The Fourier transform of the signal :

The Fourier transform of the product of with the original signal is the convolution of its transforms:

Its spectrum:

Frequency response of an LTI system defined by an ODE:

Apply the Fourier transform over the equation:

Solve for the Fourier transform of :

The frequency response of the LTI system is the ratio of the Fourier transforms of the output function over the input function :

Ordinary Differential Equations  (1)

Solve a differential equation using Fourier transforms:

Apply the Fourier transform over the equation:

Solve for the Fourier transform:

Find the inverse transform to get the solution:

Compare with DSolveValue:

Partial Differential Equations  (1)

Consider the heat equation: with initial condition :

Fourier transform with respect to :

With and , solve this ODE:

Compute the inverse Fourier transform:

And convolution to get the solution:

Consider the special case with initial condition and :

Compare with DSolveValue:

Plot the initial conditions and solutions for different values of :

Plot the solution over the - plane.

Evaluation of Integrals  (1)

Calculate the following definite integral:

Compute the Fourier transform with respect to and interchange the order of transform and integration:

Integrate over :

Use the inverse Fourier transform to get the result:

Compare with Integrate:

Other Applications  (5)

The power spectrum of a damped sinusoid:

The Fourier transform of a radially symmetric function in the plane can be expressed as a Hankel transform. Verify this relation for the function defined by:

Plot the function:

Compute its Fourier transform:

Obtain the same result using HankelTransform:

Plot the Fourier transform:

Generate a gallery of Fourier transforms for a list of radially symmetric functions:

Compute the Hankel transforms for these functions:

Generate the gallery of Fourier transforms as required:

Calculate the power spectrum of a stationary OrnsteinUhlenbeckProcess:

A quick look at the Heisenberg uncertainty principle:

Consider a fixed-area box function as the position space wavefunction of a particle. Its Fourier transform gives the momentum space wavefunction of the particle:

When is small, the height of the fixed-area box is big, and the position of the particle is almost guaranteed. The momentum space wavefunction is approximately for values between its two roots closest to zero, which makes it almost impossible to find its momentum. Similarly, vice versa, as seen here:

Properties & Relations  (6)

By default, the Fourier transform of is:

For , the definite integral becomes:

Compare with FourierTransform:

Use Asymptotic to compute an asymptotic approximation:

FourierTransform and InverseFourierTransform are mutual inverses:

FourierTransform and FourierCosTransform are equal for even functions:

FourierTransform and FourierSinTransform differ by for odd functions:

Possible Issues  (1)

The result from an inverse Fourier transform may not have the same form as the original:

Neat Examples  (2)

The Fourier transforms of weighted Hermite polynomials have a very simple form:

Create a table of basic Fourier transforms:

Wolfram Research (1999), FourierTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierTransform.html (updated 2025).

Text

Wolfram Research (1999), FourierTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierTransform.html (updated 2025).

CMS

Wolfram Language. 1999. "FourierTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/FourierTransform.html.

APA

Wolfram Language. (1999). FourierTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierTransform.html

BibTeX

@misc{reference.wolfram_2025_fouriertransform, author="Wolfram Research", title="{FourierTransform}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FourierTransform.html}", note=[Accessed: 30-January-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fouriertransform, organization={Wolfram Research}, title={FourierTransform}, year={2025}, url={https://reference.wolfram.com/language/ref/FourierTransform.html}, note=[Accessed: 30-January-2025 ]}