DSolveValue
DSolveValue[eqn,expr,x]
独立変数 x を持つ常微分方程式 eqn の記号解によって得られた expr の値を与える.
DSolveValue[eqn,expr,{x,xmin,xmax}]
xminから xmaxまでの x についての記号解を使う.
DSolveValue[{eqn1,eqn2,…},expr,…]
微分方程式のリストについての記号解を使う.
DSolveValue[eqn,expr,{x1,x2,…}]
微分方程式 eqn についての記号解を使う.
DSolveValue[eqn,expr,{x1,x2,…}∈Ω]
領域 Ω 上における偏微分方程式 eqn の解を使う.
詳細とオプション


- DSolveValueは,常微分方程式(ODE),偏微分方程式(PDE),微分代数方程式(DAE),遅延微分方程式(DDE),積分方程式,積分微分方程式,ハイブリッド微分方程式を解くことができる.
- DSolveValueの出力形式は,従属関数 u または u[x]の形式に制御される.
-
DSolveValue[eqn,u,x] f f は純関数 DSolveValue[eqn,u[x],x] f[x] f[x]は x 中の式 - DSolveValueは単一の解を返すのに対し,DSolveは複数の解を返すことができる.
- DSolveValueが与える解は,明示的に解くことができないInactiveな総和や積分を含んでいることがある.そのような場合には変数 K[1], K[2], …が使われる.
- DSolveValue[eqn,y[Infinity],x]は,Infinityにおける解 y の極限値を与える.
- DSolveValueによって解くことができる方程式のクラスには次がある.
-
u'[x]f[x,u[x]] 常微分方程式 a ∂xu[x,y]+b ∂yu[x,y]f 偏微分方程式 f[u'[x],u[x],x]0 微分代数方程式 u'[x]f[x,u[x-x1]] 遅延微分方程式 u'[x]+ 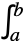 k[x,t]u[t]tf
k[x,t]u[t]tf積分微分方程式 {…,WhenEvent[cond,u[x]g]} ハイブリッド微分方程式 - DSolveValue[u[t]->sys,resp,t]は系のモデルを解くために使うことができる.sys はTransferFunctionModelまたはStateSpaceModel,応答 resp は以下のいずれかでよい. »
-
"StateResponse" 入力 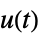 に対する sys の状態応答
に対する sys の状態応答"OutputResponse" 入力 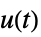 に対する sys の出力応答
に対する sys の出力応答 - DSolveValue[sys,resp,t]を使って系のモデルを解くことができる.sys はTransferFunctionModelまたはStateSpaceModel,応答 resp は以下のいずれかでよい.
-
"ImpulseResponse" 入力DiracDelta[t]に対する sys の出力応答 "StepResponse" 入力UnitStep[t]に対する sys の出力応答 "RampRespone" 入力Ramp[t]に対する sys の出力応答 - 常微分方程式および微分代数方程式の境界条件は,u[x1]a や u'[x2]b 等の特定の点で方程式を与えることで指定することができる.
- 偏微分方程式の境界条件は,方程式 u[x,y1]a,Derivative[1,0][u][x,y1]b 等として,あるいはDirichletCondition[u[x,y]g[x,y],cond]として与えることができる.
- 遅延微分方程式の初期条件は,履歴関数 g[x]として u[x/;x<x0]g[x]の形で与えることができる.
- WhenEvent[event,action]を方程式 eqn に含ませて event がTrueになったときの動作(action)を指定することができる.
- 指定 u∈Vectors[n]または u∈Matrices[{m,n}]を使って従属変数 u が順にベクトル値または行列値の変数であると示すことができる. »
- 領域 Ω は,RegionQ[Ω]がTrueになる任意のものでよい
- N[DSolveValue[...]]は,記号的に解けない微分方程式については,NDSolveValueまたはParametricNDSolveValueを呼び出す.
- 使用可能なオプション
-
Assumptions $Assumptions パラメータについての仮定 DiscreteVariables {} ハイブリッド方程式についての離散変数 GeneratedParameters C 生成されたパラメータにどのように命名するか Method Automatic 使用するメソッド - GeneratedParametersは生成されたパラメータの形式を制御する.常微分方程式および微分代数方程式については,この形式はデフォルトで定数C[n]であり,偏微分方程式については任意の関数C[n][…]である. »
例題
すべて開くすべて閉じるスコープ (118)
基本的な用法 (13)
任意定数C[1]の異なる2つの値について解の曲線をプロットする:
第2引数に y を使うことで,一階微分方程式の解を確かめる:
記号解が得られない場合は,N[DSolveValue[…]]を適用してNDSolveValueを呼び出す:
線形微分方程式 (5)
非線形微分方程式 (3)
微分方程式系 (8)
区分微分方程式 (4)
ハイブリッド微分方程式 (8)
Sturm-Liouville問題 (6)
Assumptionsを使ってこの範囲内で固有関数を求める:
積分方程式 (6)
一階偏微分方程式 (7)
任意の関数C[1]についての特定の選択による解:
ハイブリッド偏微分方程式 (11)
放物線偏微分方程式 (7)
楕円偏微分方程式 (9)
一般的な偏微分方程式 (6)
領域上の偏微分方程式 (3)
Inactive和から最初の100項を抽出する:
非整数階微分方程式 (8)
0.7階のCaputoDを含む非整数階微分方程式を解く:
系のモデル (9)
正弦波入力に対するStateSpaceModelのOutputResponseとStateResponseを計算する:
伝達関数モデルについて,ステップ応答,インパルス応答,ランプ応答を求める:
記述子StateSpaceModelの状態応答:
記述子StateSpaceModelの出力応答:
オプション (5)
Assumptions (1)
Assumptionsを使って母数 λ の範囲を指定する:
GeneratedParameters (2)
Method (1)
DifferentialRootについての解を得る:
アプリケーション (41)
常微分方程式 (12)
Infinityにおける解の極限値を計算する:
バネによって壁に固定された稼働中のコンベヤーベルト上のブロックをモデル化する.ブロックの体積,ベルトの速度,摩擦係数,バネ定数等,系のさまざまなパラメータの値について,その位置と速度を比較する:
接続に関するキルヒッホフ(Kirchhoff)の法則に加えて構成成分の諸法則を使って,時間 ![]() で適用される電圧
で適用される電圧 ![]() のステップインパルスに対するRLC回路の応答のシミュレーションを行う:
のステップインパルスに対するRLC回路の応答のシミュレーションを行う:
水がパイプを通って1つのタンクから別のタンクに流れるときの,2つの円筒形タンクの水位の変化をモデル化する:
Hagen–Poiseuille関係を使ってパイプの中のフローをモデル化する:
積分方程式 (4)
等時曲線問題では,ビーズ玉が,どこに置かれたものであれ,同じ時間で最下点まで落ちる下降曲線を求める必要がある.合計の下降時間を曲線の弧長と速度 v によって表すとアベルの積分方程式 ![]() が与えられる.未知の関数
が与えられる.未知の関数 ![]() を関係
を関係 ![]() によって定義し,エネルギー保存の方程式
によって定義し,エネルギー保存の方程式 ![]() の変換を使うと明示的な方程式が与えられる:
の変換を使うと明示的な方程式が与えられる:
DSolveValueを使って積分方程式を解く:
積分が実数値であるという仮定のもとに曲線を原点から始めて積分すると,![]() の関数としての
の関数としての ![]() が与えられる:
が与えられる:
![]() と
と ![]() の値を代入し,ParametricPlotを使って最大等時曲線を表示する:
の値を代入し,ParametricPlotを使って最大等時曲線を表示する:
変数 ![]() を変更すると,
を変更すると,![]() の範囲での曲線の単純で特異ではないパラメータ化が与えられる:
の範囲での曲線の単純で特異ではないパラメータ化が与えられる:
エネルギーの保存方程式とチェーン規則![]() を組み合せると,
を組み合せると,![]() の関数としての
の関数としての ![]() について次の微分方程式が得られる:
について次の微分方程式が得られる:
解をプロットするとすべてが2秒で最下点 ![]() に達することが分かる:
に達することが分かる:
3gの質量が付けられたバネ質量系は3dynes/cmのバネ定数と2g/sの減衰係数を持つ.![]() で質量が下方に押され,速度28cm/sで下向きに放たれる.
で質量が下方に押され,速度28cm/sで下向きに放たれる.![]() で
で![]() の力が質量に対して下向きにかかる.系の速度を時間の関数として求める.速度についての積分方程式は以下で与えられる:
の力が質量に対して下向きにかかる.系の速度を時間の関数として求める.速度についての積分方程式は以下で与えられる:
DSolveValueを使って積分微分方程式を解く:
 ,インダクタンスは,キャパシタンスはである.抵抗器中の電流は最初はである.電流を時間の関数として求める:
,インダクタンスは,キャパシタンスはである.抵抗器中の電流は最初はである.電流を時間の関数として求める:
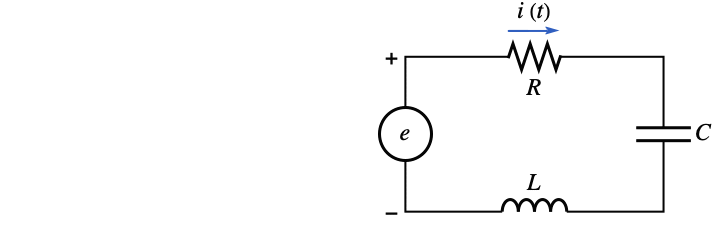
DSolveValueを使って積分微分方程式を解く:
線形ヴォルテラ積分方程式は線形微分方程式の初期値問題に等しい.この関係を次のヴォルテラ方程式について確かめる:
DSolveValueを使って積分方程式を解く:
従来の偏微分方程式 (5)
一般的な偏微分方程式 (5)
粘度パラメータが無限に小さくなる場合の,極限におけるバーガース方程式の平滑化解の衝撃波への進化を見る:
長さ d の一次元の箱の中で動くように条件付けられた電子は,端点にディリクレ条件がある自由シュレディンガー方程式に支配されている:
和の中の各項は,正弦を初期状態として使うと確率密度定 ![]() が時間依存になるので,常状態と呼ばれる.例えば,以下のようになる:
が時間依存になるので,常状態と呼ばれる.例えば,以下のようになる:
初期データの正規化は,密度の積分(どこかに粒子を発見する全確率)が1になるように選択される:
上記以外の初期条件を使うと,たとえ2つの定常状態の和のように単純なものでも,結果として複雑な時間依存密度になる:
電子質量と ![]() の値をSI単位で入れ,d をよく使われる原子間距離の1nmに設定すると,次の密度関数になる:
の値をSI単位で入れ,d をよく使われる原子間距離の1nmに設定すると,次の密度関数になる:
このグラフを確率密度の動画として見ると,電子の「中心」がボックスの片側からもう片側に動くのが分かる:
ブラック・ショールズモデルを使って,もとになっている資産価格と行使価格の両方が100ドル,安全金利5%,もとになっている資産のボラティリティが20%,満期1年の場合の,ヨーロッパバニラコールオプションの値を求める:
FinancialDerivativeで与えられた値と比較する:
系のモデル (5)
UnilateralConvolveを使って正弦波入力からのモデルの出力応答を得る:
次は,インパルス応答と正弦波関数のラプラスたたみ込みを示している:
正弦波入力からの出力応答をDSolveValueを使って計算する:
単位ステップ入力に応じて,安定した1次系の定常状態の出力値を決定する:
望ましい生産率と販売率を入力として,実際の生産率と在庫レベルを状態として持つ生産および在庫システムモデルの状態空間モデル:
特定の生産率と初期の平衡状態からの売上の10%の増加に対する応答を決定する:
Clohessy–Wiltshire方程式は,中心体を周回する2つの衛星間の相対運動をモデル化する:
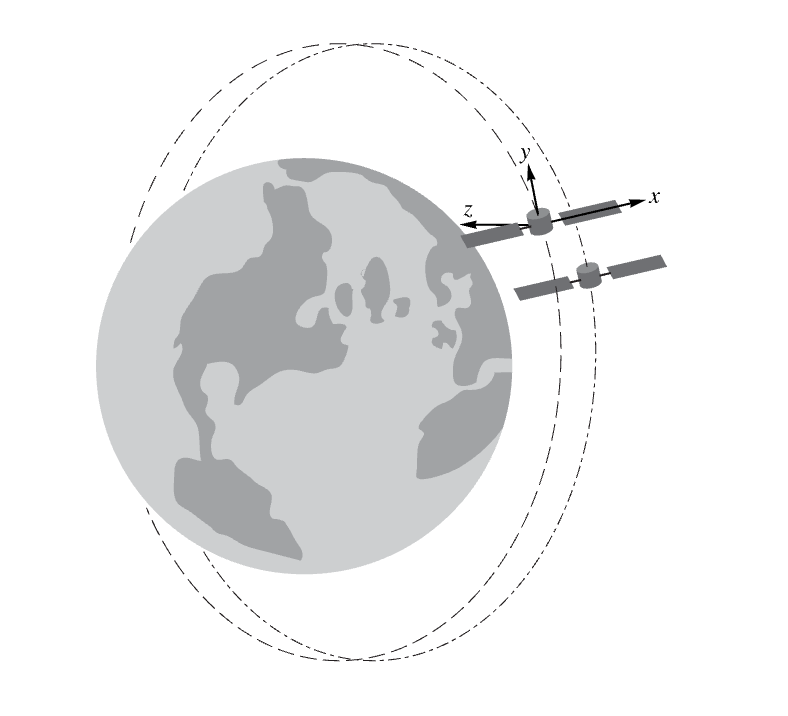
DSolveValueを使って,打上げ条件の特定の集合から閉じた相対軌道を得る:
特性と関係 (12)
DSolveValueは解の式を返す:
DSolveは解についての規則を返す:
Integrateに対応する微分方程式:
NDSolveValueを使って数値解を求める:
AsymptoticDSolveValueを使って漸近展開を求める:
DEigensystemを使って固有値と固有関数を求める:
DSolveValueを使ってインパルス応答を計算する:
InverseLaplaceTransformを使った同じ計算:
記号解が得られなかったときには,N[DSolveValue[…]]を適用してNDSolveValueを呼び出す:
CompleteIntegralは非線形偏微分方程式の完全積分を求める:
DSolveValueは同じ解を警告メッセージとともに返す:
CompleteIntegralを使って線形偏微分方程式の完全積分を求める:
DSolveValueはこの偏微分方程式についての一般解を返す:
DFixedPointsを使って2つの常微分方程式系の固定点を求める:
DStabilityConditionsを使って固定点の安定性を解析する:
考えられる問題 (4)
テキスト
Wolfram Research (2014), DSolveValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/DSolveValue.html (2024年に更新).
CMS
Wolfram Language. 2014. "DSolveValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/DSolveValue.html.
APA
Wolfram Language. (2014). DSolveValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DSolveValue.html