表示一个网络图层,将一元函数 f 应用于输入数组的每一个元素.
ElementwiseLayer["name"]
应用由 "name" 指定的函数.


ElementwiseLayer
表示一个网络图层,将一元函数 f 应用于输入数组的每一个元素.
ElementwiseLayer["name"]
应用由 "name" 指定的函数.
更多信息和选项


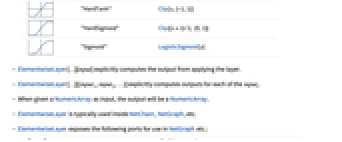
- f 可为以下任一函数:Ramp、LogisticSigmoid、Tan、Tanh、ArcTan、ArcTanh、Sin、Sinh、ArcSin、ArcSinh 、Cos、Cosh、ArcCos、ArcCosh、Cot、Coth、ArcCot、ArcCoth、Csc、Csch、ArcCsc、ArcCsch、Sec、Sech、ArcSec、ArcSech、Haversine、InverseHaversine、Gudermannian、InverseGudermannian、Log、Exp、Sqrt、CubeRoot、Abs、Gamma、LogGamma、Erf、InverseErf、Erfc、InverseErfc、Round、Floor、Ceiling、 Sign、FractionalPart、IntegerPart、Unitize、KroneckerDelta.
- 通常,f 可以是在应用于单个参数时给出 Ramp、LogisticSigmoid 等与数字、Plus、Subtract、Times、Divide、Power、Surd、Min、Max、Clip、Mod、Threshold、Chop 以及使用 If、And、Or、Which、Piecewise、Equal、Greater、GreaterEqual、Less、LessEqual、Unequal、Negative、NonNegative、Positive、NonPositive 、PossibleZeroQ 的逻辑运算的组合的任意对象.
- ElementwiseLayer 支持 "name" 具有下列值:
-
"RectifiedLinearUnit" or "ReLU" Ramp[x] 
"ExponentialLinearUnit" or "ELU" x 当 x≥0 Exp[x]-1 当 x<0 
"ScaledExponentialLinearUnit" or "SELU" 1.0507 x 当 x >= 0 1.758099340847161` (Exp[x]-1) 当 x<0 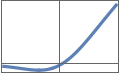
"GaussianErrorLinearUnit" or "GELU" 0.5 x(1+Erf[x/Sqrt[2]]) 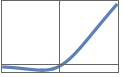
"Swish" x LogisticSigmoid[x] 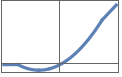
"HardSwish" x Min[Max[x+3,0],6]/6 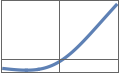
"Mish" x Tanh[Log[1+Exp[x]]] 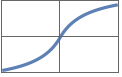
"SoftSign" x/(1+Abs[x]) 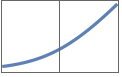
"SoftPlus" Log[Exp[x]+1] 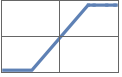
"HardTanh" Clip[x,{-1,1}] 
"HardSigmoid" Clip[(x+1)/2, {0,1}] 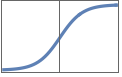
"Sigmoid" LogisticSigmoid[x] - ElementwiseLayer[…][input] 显式计算应用网络层所得到的输出.
- ElementwiseLayer[…][{input1,input2,…}] 显式计算每个 inputi 的输出.
- 当 NumericArray 作为输入时,输出将是 NumericArray.
- ElementwiseLayer 通常用于 NetChain、NetGraph 等内部.
- ElementwiseLayer 公开了以下端口,以用于 NetGraph 等中:
-
"Input" 任意秩的数组 "Output" 与输入相同维数的数组 - 当无法从更大的网络的其他层推断时,选项 "Input"->{n1,n2,…} 可用于修复 ElementwiseLayer 的输入维度.
- Options[ElementwiseLayer] 给出构建网络层的默认选项的列表. Options[ElementwiseLayer[…]] 给出在一些数据上运行网络层的默认选项列表.
- Information[ElementwiseLayer[…]] 给出关于该网络层的报告.
- Information[ElementwiseLayer[…],prop] 给出 ElementwiseLayer[…] 的属性 prop 的值. 可能的属性与 NetGraph 相同.
范例
打开所有单元 关闭所有单元基本范例 (2)
范围 (3)
创建一个计算 "hard sigmoid" 函数的 ElementwiseLayer:
创建一个接受大小为 3 的向量的 ElementwiseLayer:
创建计算高斯函数的 ElementwiseLayer:
应用 (3)
训练 G. Klambauer 等于 2017 年在 UCI Letter 数据集中的 "Self-Normalizing Neural Networks" 中描述的 16 层深的自规一化网络. 获取数据:
自规一化网络假定输入数据的均值为 0,方差为 1. 标准化测试和训练数据:
定义一个 16 层、具有 "AlphaDropout" 的自规一化的网络:
与用 Classify 中的 "RandomForest" 方法所得的准确度相比较:
允许分类网络处理“非分离”问题. 创建一个由圆盘上的点组成的合成训练集,由圆 r=0.5 分成两类:
创建一个由两个 LinearLayer 层构建的层,最后使用 ElementwiseLayer 变换成概率:
因为 LinearLayer 是一个仿射层,没有涉及非线性的叠加两层相当于使用一个单层. 平面上的单线不能分离这两类,它是单个 LinearLayer 的水平集.
训练类似的网络,其在两层间具有 Tanh 非线性:
二进制分类任务需要网络的输出是一个概率. ElementwiseLayer[LogisticSigmoid] 可用于接受任何标量并产生介于 0 和 1 之间的值. 创建一个网络,接受长度为 2 的向量并产生二进制预测:
属性和关系 (1)
当在 NetChain 或 NetGraph 中指定合适的函数会自动使用 ElementwiseLayer:
可能存在的问题 (3)
技术笔记
相关指南
-
▪
- 神经网络层
文本
Wolfram Research (2016),ElementwiseLayer,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ElementwiseLayer.html (更新于 2022 年).
CMS
Wolfram 语言. 2016. "ElementwiseLayer." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/ElementwiseLayer.html.
APA
Wolfram 语言. (2016). ElementwiseLayer. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ElementwiseLayer.html 年
BibTeX
@misc{reference.wolfram_2025_elementwiselayer, author="Wolfram Research", title="{ElementwiseLayer}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ElementwiseLayer.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_elementwiselayer, organization={Wolfram Research}, title={ElementwiseLayer}, year={2022}, url={https://reference.wolfram.com/language/ref/ElementwiseLayer.html}, note=[Accessed: 05-February-2026]}