FindDistribution[data]
data の分布にフィットする単純な関数形式を求める.
FindDistribution[data,n]
最良の分布を n 個まで求める.
FindDistribution[data,n,prop]
特性 prop と関連する最良の分布を n 個まで返す.
FindDistribution[data,n,{prop1,prop2,…}]
特性 prop1,prop2等に関連する最良の分布を n 個まで返す.


FindDistribution
FindDistribution[data]
data の分布にフィットする単純な関数形式を求める.
FindDistribution[data,n]
最良の分布を n 個まで求める.
FindDistribution[data,n,prop]
特性 prop と関連する最良の分布を n 個まで返す.
FindDistribution[data,n,{prop1,prop2,…}]
特性 prop1,prop2等に関連する最良の分布を n 個まで返す.
詳細とオプション



- データは,一変量分布からの可能な結果のリストでなければならない.
- FindDistribution[data,n,All]は,可能なすべての特性を持つDatasetオブジェクトを作成する.
- サポートされる特性
-
"BIC" ベイズ情報量基準 "AIC" 赤池情報量基準 "HQIC" Hannan–Quinn情報量基準 "Score" 内部スコア "Complexity" 分布の複雑さ "LogLikelihood" LogLikelihood 値 "PearsonChiSquare" PearsonChiSquareTest p 値 "CramerVonMises" CramerVonMisesTest p 値 All 上記の特性すべて - 使用可能なオプション
-
MaxItems Infinity 混合分布における分布の最高数 PerformanceGoal Automatic パフォーマンスのどの面について最適化するか RandomSeeding Automatic どのような擬似乱数生成器のシードを内部的に使うべきか TargetFunctions Automatic 考慮する分布タイプ - PerformanceGoalの可能な設定
-
"Speed" 分布を求めるために使用する時間を最短にする "Quality" よりよい分布を求めようとする - TargetFunctionsの可能な設定
-
Automatic 自動選択された分布 All すべての組込み分布 "Continuous" すべての連続分布 "Discrete" すべての離散分布 {dist1, 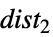 ,
, }
}分布 disti { 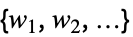 {dist1,
{dist1,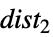 ,
, }}
}}重み wiを使った分布 disti - RandomSeedingの可能な設定
-
Automatic 関数が呼び出されるたびに自動的にシードを変える Inherited 外部シードの乱数を使う seed 明示的な整数または文字列をシードとして使う - TargetFunctionsで使用可能な連続分布には,BetaDistribution,CauchyDistribution,ChiDistribution,ChiSquareDistribution,ExponentialDistribution,ExtremeValueDistribution,FrechetDistribution,GammaDistribution,GumbelDistribution,HalfNormalDistribution,InverseGaussianDistribution,LaplaceDistribution,LevyDistribution,LogisticDistribution,LogNormalDistribution,MaxwellDistribution,NormalDistribution,ParetoDistribution,RayleighDistribution,StudentTDistribution,UniformDistribution,WeibullDistribution,HistogramDistributionがある.
- TargetFunctionsで使用可能な離散分布には,BenfordDistribution,BinomialDistribution,BorelTannerDistribution,DiscreteUniformDistribution,GeometricDistribution,LogSeriesDistribution,NegativeBinomialDistribution,PascalDistribution,PoissonDistribution,WaringYuleDistribution,ZipfDistribution,HistogramDistribution,EmpiricalDistributionがある.
- 内部情報量基準には,ベイズ情報基準をTargetFunctionsの確率とともに使う.
例題
すべて開く すべて閉じる例 (2)
スコープ (3)
デフォルトで,FindDistributionは単純な分布を返す:
上位2分布についての全特性を含むDatasetを生成する:
オプション (5)
TargetFunction (3)
連続的であるとして扱われた場合のデータの分布をGammaDistributionを使って推定する:
特定の分布についての母数を,その分布についての事前分布を仮定して推定する:
1935年から1989年までの米国の地震のマグニチュードには2つの峰がある:
TargetFunctionsを使わずに最良フィットを推定する:
PerformanceGoal (1)
ビッグデータの集合について最良フィットを推定し,PerformanceGoalのさまざまな設定についてAbsoluteTimingを比較する:
解のLogLikelihoodを比較する:
RandomSeeding (1)
アプリケーション (5)
特性と関係 (1)
デフォルトで,FindDistributionParametersは最大尤度を使って固定分布の分布母数を推定する.FindDistributionはベイズ情報量基準と事前確率と組み合せる完全なベイズ的アプローチを使って最適な分布と最適な母数の両方を求める.
StudentTDistributionからサンプルを取ってデータを生成する:
FindDistributionを使ってこのデータに最もフィットする分布を推定する:
FindDistributionParametersを使い,StudentTDistributionを仮定して最適な母数を推定する:
StudentTDistributionは対数尤度を最小にするが,LogisticDistributionはこれに比べて事前確率が高く複雑さは低い.
対応するLogLikelihoodと比較する:
FindDistributionParametersとほぼ同じ母数を求めないなら,オプションTargetFunctionsを使うとよい:
テキスト
Wolfram Research (2015), FindDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/FindDistribution.html (2017年に更新).
CMS
Wolfram Language. 2015. "FindDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/FindDistribution.html.
APA
Wolfram Language. (2015). FindDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindDistribution.html
BibTeX
@misc{reference.wolfram_2025_finddistribution, author="Wolfram Research", title="{FindDistribution}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/FindDistribution.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_finddistribution, organization={Wolfram Research}, title={FindDistribution}, year={2017}, url={https://reference.wolfram.com/language/ref/FindDistribution.html}, note=[Accessed: 06-February-2026]}