RegionPlot
RegionPlot[pred,{x,xmin,xmax},{y,ymin,ymax}]
pred がTrueである領域を見せるプロットを作成する.
RegionPlot[{pred1,pred2,…},…]
prediに対応する複数の領域をプロットする.
RegionPlot[{…,w[predi,…],…},…]
特徴を記号ラッパー w で定義して prediをプロットする.
詳細とオプション



- 述部 pred は不等式の任意の論理結合でよい.
- RegionPlotでプロットされる領域には不連続な部分が含まれることがある.
- RegionPlotは,変数 x と y を,事実上Blockを使って局所的なものとして扱う.
- RegionPlotは属性HoldAllを有し,特定の数値を x と y に割り当てた後ではじめて pred を評価する.場合によってはEvaluateを使ってまず pred を記号的に評価した方が効率的かもしれない.
- prediには次のラッパー w を使うことができる.
-
Annotation[predi,label] prediの注釈を与える Button[predi,action] prediの曲線がクリックされたときに action を評価する Callout[predi,label] コールアウトで領域にラベルを付ける Callout[predi,label,pos] コールアウトを相対的な位置 pos に置く EventHandler[predi,events] prediの一般的なイベントハンドラを定義する Hyperlink[predi,uri] 領域をハイパーリンクにする Labeled[predi,label] 領域にラベルを付ける Labeled[predi,label,pos] ラベルを相対的な位置 pos に置く Legended[predi,label] 領域を凡例で識別する PopupWindow[predi,cont] 領域にポップアップウィンドウを付ける StatusArea[predi,label] マウスオーバーの際にステータスエリアに表示する Style[predi,styles] 領域を指定されたスタイルで表示する Tooltip[predi,label] 領域にツールチップを付ける Tooltip[predi] 領域をツールチップとして使う - ラッパー w は複数のレベルで適用できる.
-
w[predi] prediをラップする w[{predi,…}] prediの集合をラップする w1[w2[…]] ネストしたラッパーを使う - Callout,Labeled,Placedには次の位置 pos が使える.
-
Automatic 自動的に置かれたラベル Above, Below, Before, After 曲線の周囲の位置 {x,y} {x,y}の近くの位置 {pos,epos} 領域の相対的な位置 pos に置かれたラベル内の epos - RegionPlotはGraphicsと同じオプションに以下の追加・変更を加えたものが設定できる. [全オプションのリスト]
-
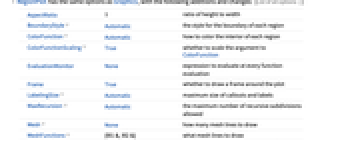
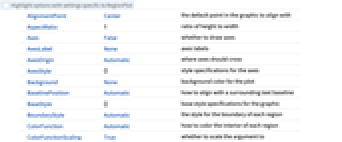
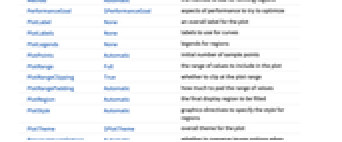
AspectRatio 1 縦横比 BoundaryStyle Automatic 各領域の境界のスタイル ColorFunction Automatic 各領域の内側の彩色をどうするか ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか EvaluationMonitor None すべての関数評価で評価される式 Frame True プロットの周囲に枠を描くかどうか LabelingSize Automatic コールアウトとラベルの最大サイズ MaxRecursion Automatic 許容される再帰分割の最大数 Mesh None メッシュラインを何本引くか MeshFunctions {#1&,#2&} どのようなメッシュラインを描くか MeshShading None メッシュライン間の領域の陰影付けをどうするか MeshStyle Automatic メッシュラインのスタイル Method Automatic 領域を細分化するためのメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotLabels None 曲線に使うラベル PlotLegends None 領域の凡例 PlotPoints Automatic サンプル点の初期数 PlotRange Full プロットに含める値の範囲 PlotRangeClipping True プロット範囲で切り取るかどうか PlotRangePadding Automatic 値の範囲をどの程度充填するか PlotStyle Automatic 領域のスタイルを指定するグラフィックス指示子 PlotTheme $PlotTheme プロットの全体的なテーマ ScalingFunctions None 個々の座標をどのようにスケールするか TextureCoordinateFunction Automatic テクスチャ座標をどのように決めるか TextureCoordinateScaling True TextureCoordinateFunctionの引数をスケールするかどうか WorkingPrecision MachinePrecision 内部計算に使われる精度 - PlotLegendsの代表的な設定値
-
None 凡例は付けない Automatic 凡例を自動的に決定する "Expressions" f1, f2, … を凡例ラベルとして使う {lbl1,lbl2,…} lbl1, lbl2, … を凡例ラベルとして使う Placed[lspec,…] 凡例の置き方を指定する - RegionPlotはまず,PlotPointsで指定された等間隔のサンプル点の格子で pred を評価する.次に適応的アルゴリズムを用いて,pred がTrueとなるすべての領域の境界を求めるために最高MaxRecursion回まで再分割する.
- RegionPlotは有限個のサンプル点しか使わないので,pred がTrueとなる領域を見落す可能性もある.結果の検証にはPlotPointsとMaxRecursionの設定値を大きくしてみるとよい.
- デフォルト設定のPlotRange->Fullの場合,RegionPlotは x と y について xminから xmaxまでと yminから ymaxまでの完全な範囲を明示的に含む.
- Mesh->Allの設定では,RegionPlotは各領域を求めるために使ったすべての部分分割を表示するように明示的にメッシュラインを描く.
- RegionPlotは一般に正の領域のみを見付けることができる.線のみあるいは点のみの領域は見付けられない.
- MeshFunctionsの関数に渡される引数は x, y である.ColorFunctionとTextureCoordinateFunctionにはデフォルトでこれらの引数のスケールされたものが渡される.
- ScalingFunctions{sx,sy}は x 軸を sxで,y 軸を syでスケールする.
- 次は,よく使われる組込みのスケーリング関数 s である.
-
"Log" 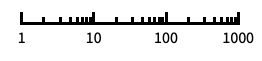
自動の目盛ラベルが付いた対数スケール "Log10" 
10のベキ乗に目盛がある底10の対数スケール "SignedLog" 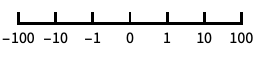
0と負の数を含む対数スケール "Reverse" 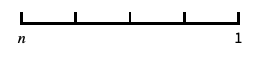
座標の向きを反転させる "Infinite" 
無限スケール - RegionPlotはGraphics[GraphicsComplex[data]]を返す.

全オプションのリスト


例題
すべて開くすべて閉じるスコープ (19)
サンプリング (5)
ラベル付けと凡例 (4)
Labeledで領域にラベルを付ける:
Calloutで領域にラベルを付ける:
ラベルが領域内に置かれるときは,コールアウトのリーダーは無効になる:
PlotLegendsで凡例を加える:
Legendedで凡例を加える:
プレゼンテーション (10)
領域に明示的なPlotStyleを与える:
範囲の境界に明示的なBoundaryStyleを与える:
オプション (56)
BoundaryStyle (4)
ColorFunction (5)
ColorFunctionはPlotStyleよりも優先順位が高い:
ColorFunctionはMeshShadingよりも優先順位が低い:
Mesh (7)
MeshShading (4)
PlotLegends (8)
PlotStyle (5)
ScalingFunctions (5)
Infinityを含む領域は自動的にスケールされる:
アプリケーション (8)
特性と関係 (9)
RegionPlotは,必要に応じてより多くの点をサンプルとして取る:
立体についてはRegionPlot3Dを使う:
方程式系にContourPlotとContourPlot3Dを使う:
複素平面上の領域にComplexRegionPlotを使う:
他のプロットを抑制するためにRegionFunctionを使う:
平面のパラメトリック曲線や領域にParametricPlotを使う:
領域上での積分にIntegrateあるいはNIntegrateを使う:
Maximize,NMaximizeあるいはFindMaximumを使って領域上で最適化する:
Reduceを使って領域の円柱表示をする:
FindInstanceを使って領域内の特定のサンプルを得る:
考えられる問題 (2)
テキスト
Wolfram Research (2007), RegionPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/RegionPlot.html (2022年に更新).
CMS
Wolfram Language. 2007. "RegionPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/RegionPlot.html.
APA
Wolfram Language. (2007). RegionPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionPlot.html