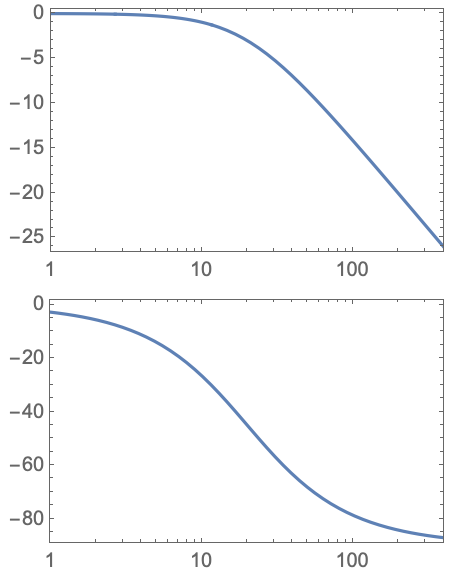
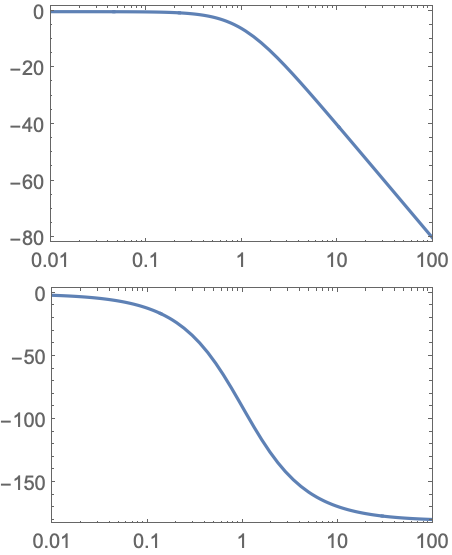
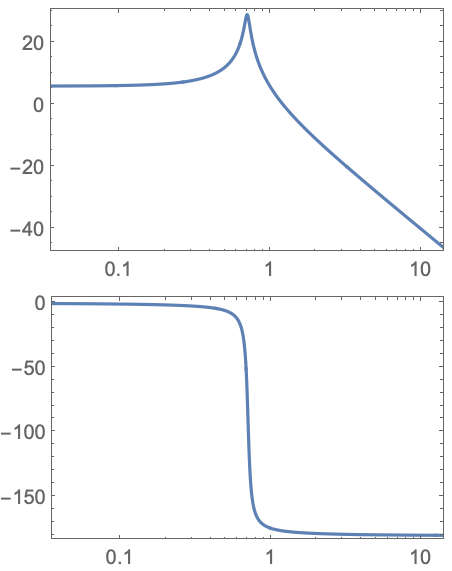
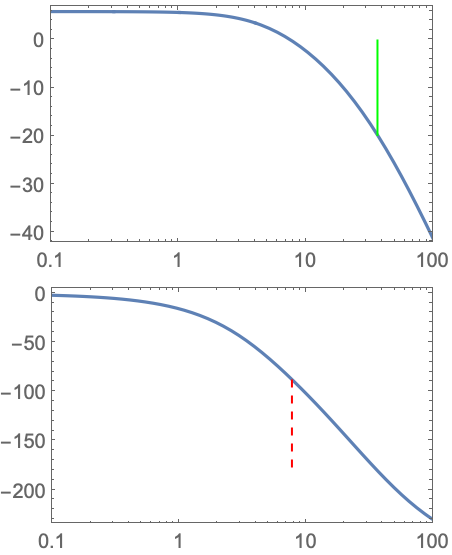
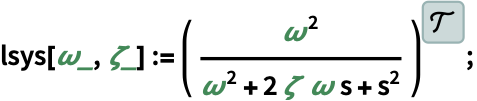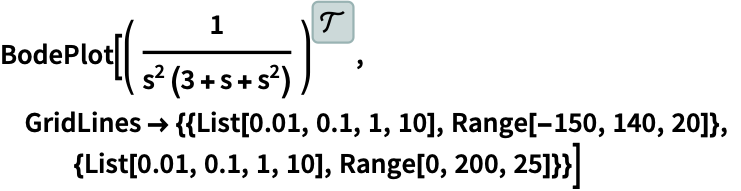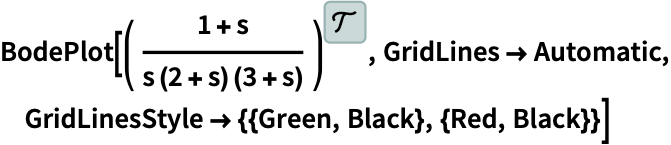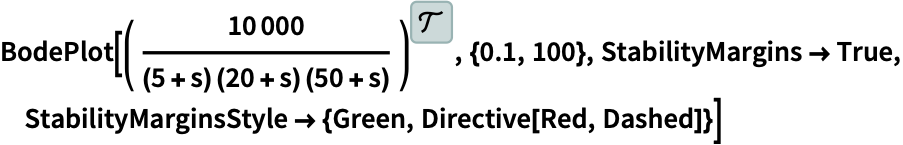BodePlot
✖
BodePlot
詳細とオプション




- BodePlotは lsys の伝達関数のゲインと位相の線図を与える.
- 系 lsys はディスクリプタ系と遅延系を含むTransferFunctionModelまたはStateSpaceModelである.
- 対応する伝達関数
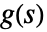 がある系 lsys に対しては,次の式の線図が与えられる.
がある系 lsys に対しては,次の式の線図が与えられる. -
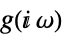
連続時間系 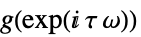
サンプル時間 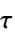 の離散時間系
の離散時間系 - BodePlotは,事実上Blockを使い,変数 ω を局所的なものとして扱う.
- BodePlotにはPlotと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
Exclusions None 除外する周波数 FeedbackType "Negative" フィードバックタイプ Frame True 各プロットに枠を描くかどうか MeshFunctions {{#1&},{#1&}} メッシュ区分の置き方の決め方 PhaseRange Automatic 使用する位相値の範囲 PlotLayout "VerticalGrid" 使用するレイアウト PlotRange {{Full,Automatic},{Full,Automatic}} 含める値の範囲 SamplingPeriod None サンプリング周期 ScalingFunctions {{"Log10","dB"},{"Log10","Degree"}} スケーリング関数 StabilityMargins False 安定余裕を示すかどうか StabilityMarginsStyle Automatic 安定余裕のスタイルを指定するグラフィックス指示子 - オプションPlotLayoutで使える明示的な設定値は"VerticalGrid"と"List"である.
- オプションPlotLayoutには次の値が使える.
-
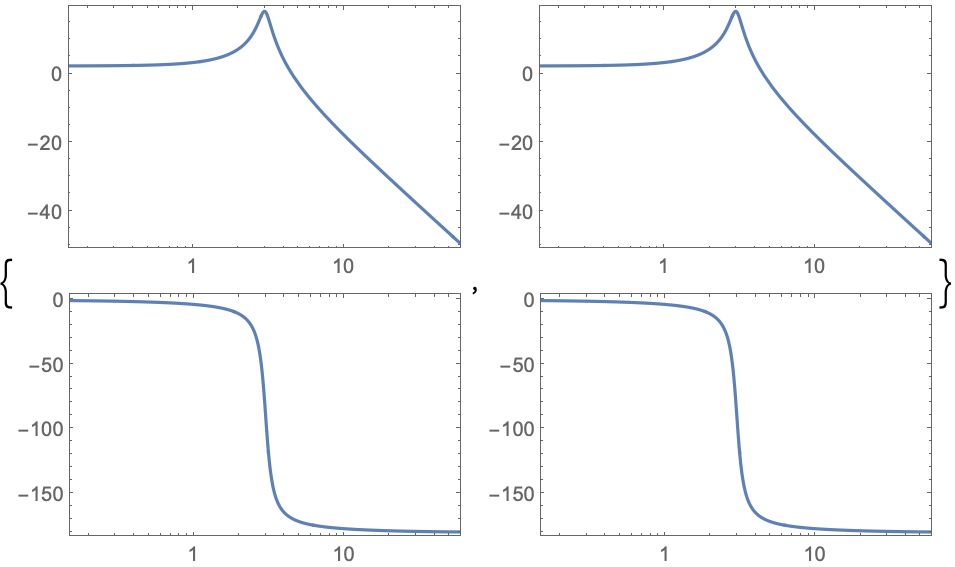
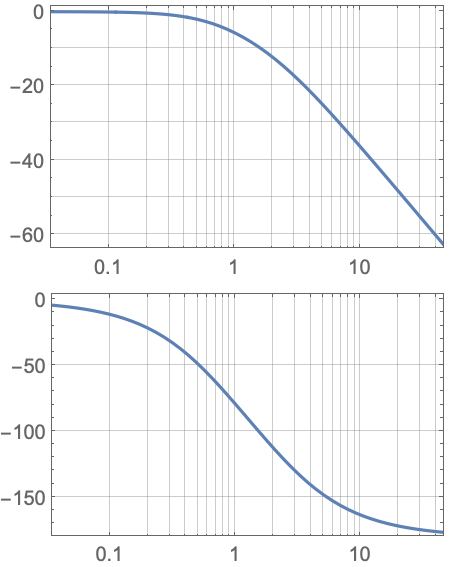
"VerticalGrid" ゲイン線図と位相線図を垂直格子で {  ,
, }
}"List" ゲイン線図と位相線図をリストで 
"Magnitude" ゲイン線図のみ 
"Phase" 位相線図のみ - BodePlotの他のオプションは,最初の要素がゲイン線図,2番目が位相線図を表す,2つの要素のリストとして指定できる.
- オプション指定
-
opt->val val をゲインと位相の両線図に使う opt->{val} val をゲイン線図に,デフォルト値を位相線図に使う opt->{val1,val2} val1をゲイン線図に,val2を位相線図に使う opt->{Automatic,val} デフォルト値をゲイン線図に,val を位相線図に使う - PlotLayoutの設定が"Magnitude"あるいは"Phase"のとき,単一の設定は要求された線図を参照する.
- スケーリング関数はScalingFunctions{{magfreqscale,magscale},{phasefreqscale,phasescale}}で指定できる.
- 周波数スケール magfreqscale と phasefreqscale には,10を底とする対数スケールを表す"Log10"と線形スケールを表す"Linear"が使える.
- ゲインスケール magscale にはそれぞれゲインのデシベルと絶対値を表す"dB"あるいは"Absolute"が使える.
- 位相スケール phasescale には"Degree"あるいは"Radian"が使える.
全オプションのリスト
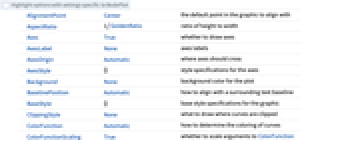



例題
すべて開くすべて閉じる例 (3)基本的な使用例
スコープ (13)標準的な使用例のスコープの概要
https://wolfram.com/xid/0i1r4wou6-yglej9
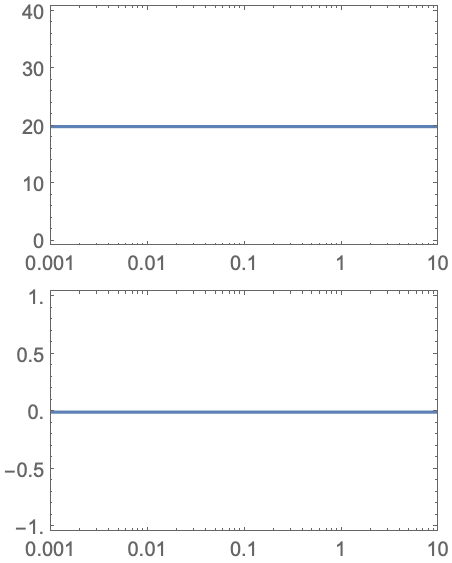
https://wolfram.com/xid/0i1r4wou6-emlvr9
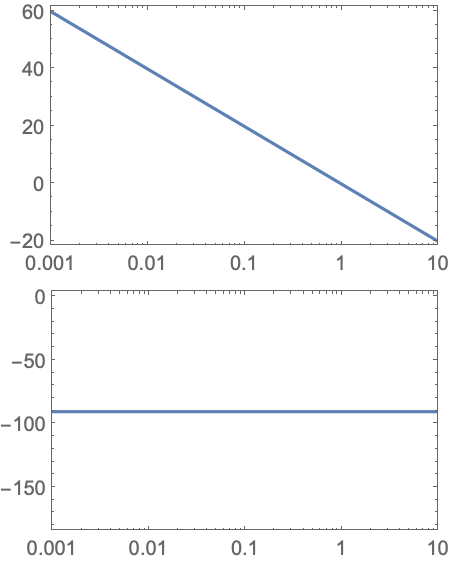
https://wolfram.com/xid/0i1r4wou6-isayy3
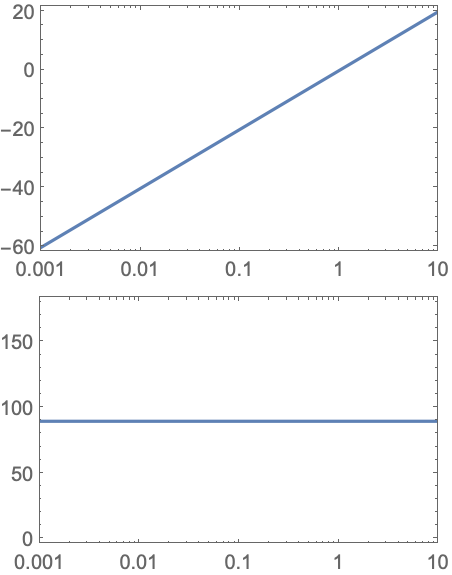
https://wolfram.com/xid/0i1r4wou6-2v78e
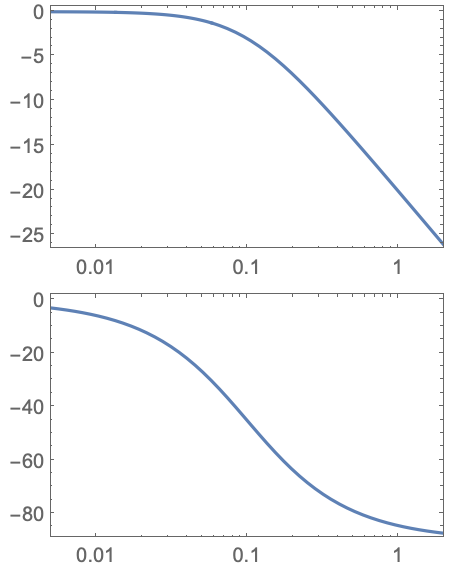
https://wolfram.com/xid/0i1r4wou6-8gnze1
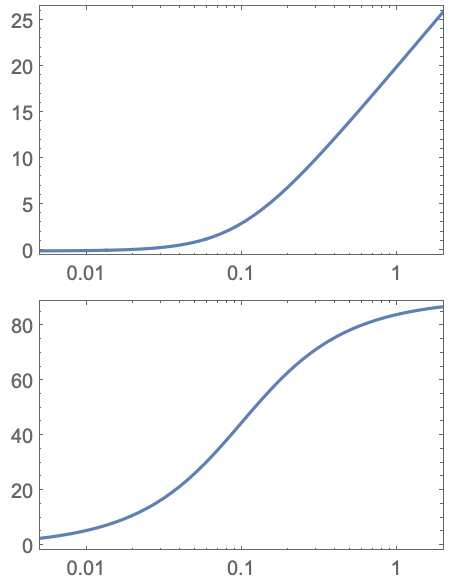
https://wolfram.com/xid/0i1r4wou6-9seqte
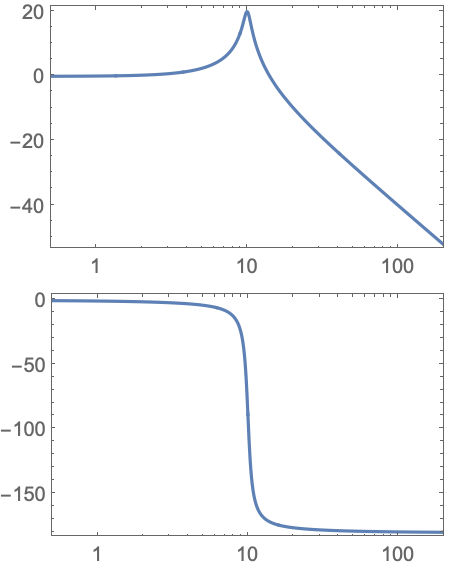
https://wolfram.com/xid/0i1r4wou6-8u8y7a
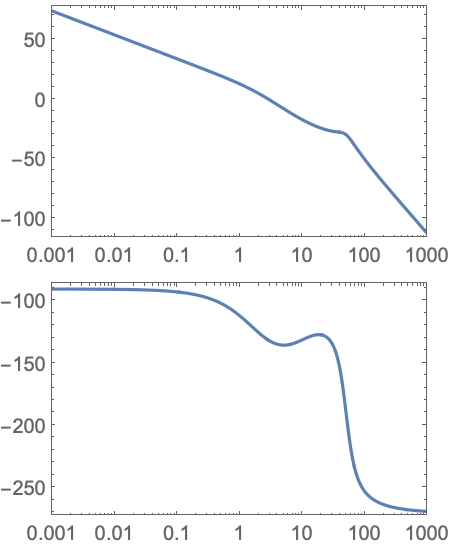
https://wolfram.com/xid/0i1r4wou6-uqcvn4
https://wolfram.com/xid/0i1r4wou6-0365c3
https://wolfram.com/xid/0i1r4wou6-byg9e2

https://wolfram.com/xid/0i1r4wou6-7ex9ln
https://wolfram.com/xid/0i1r4wou6-xhe5nt
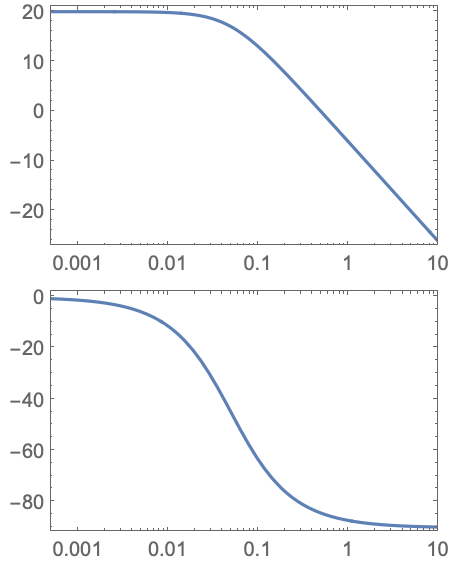
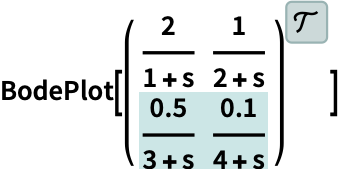
https://wolfram.com/xid/0i1r4wou6-3ij4am
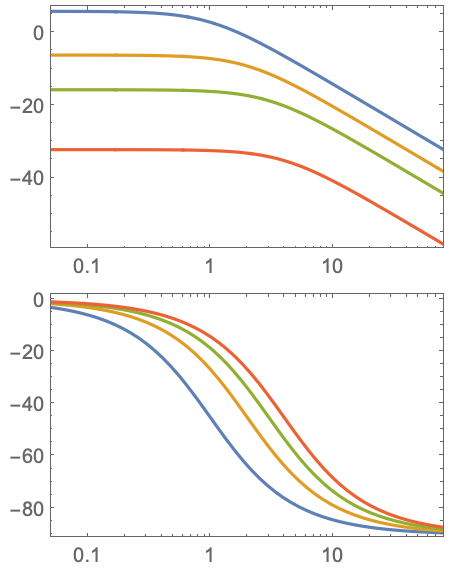
一般化と拡張 (1)一般化および拡張された使用例
オプション (21)各オプションの一般的な値と機能
CoordinatesToolOptions (5)
https://wolfram.com/xid/0i1r4wou6-2nyrb8
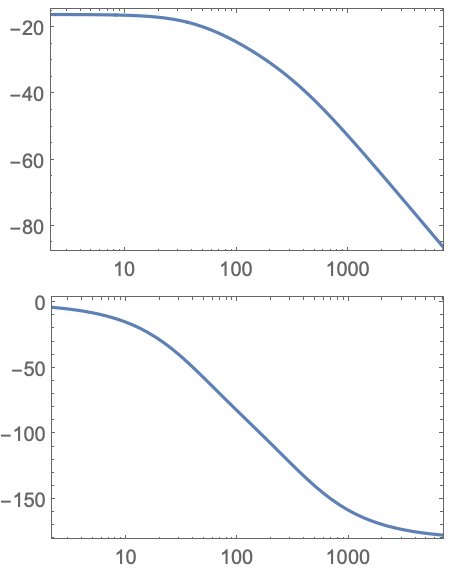
周波数rad/sであるなら,これを![]() で割って座標周波数の値をHzで得る:
で割って座標周波数の値をHzで得る:

https://wolfram.com/xid/0i1r4wou6-57jeib
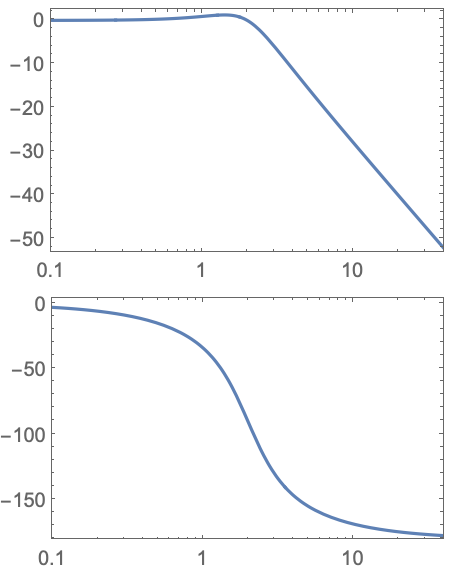

https://wolfram.com/xid/0i1r4wou6-bvfkm8
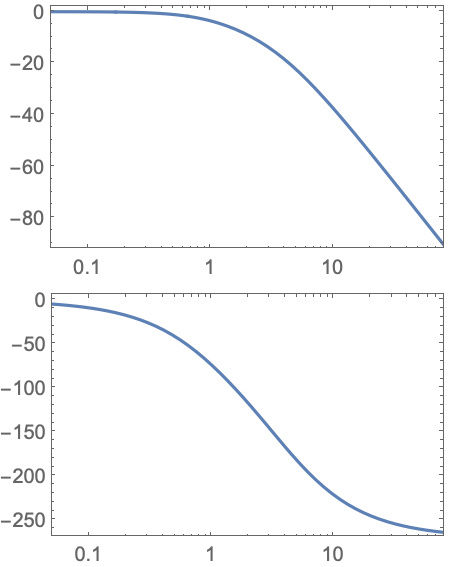
もとの単位による周波数値,絶対単位によるゲイン,ラジアンによる位相:

https://wolfram.com/xid/0i1r4wou6-l04qzn
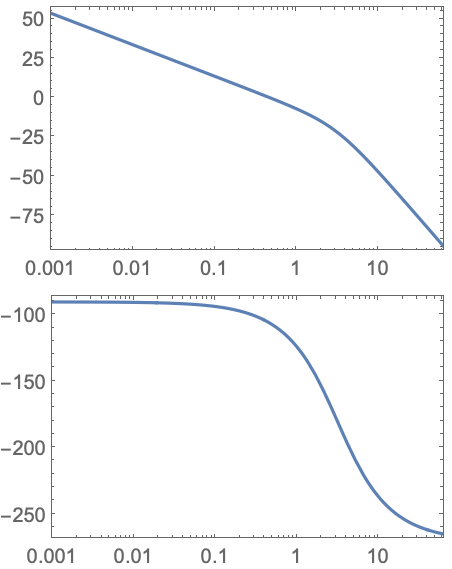

https://wolfram.com/xid/0i1r4wou6-r43x4j
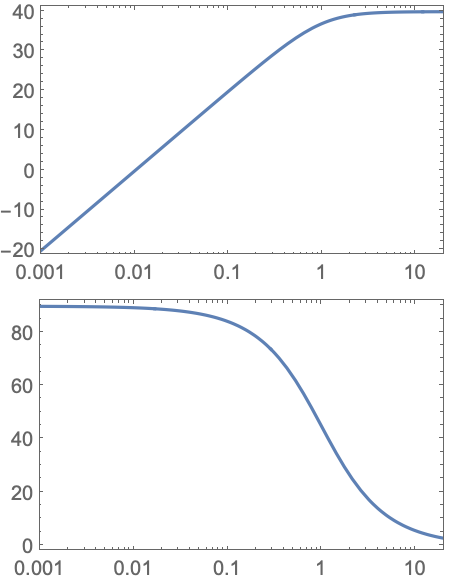
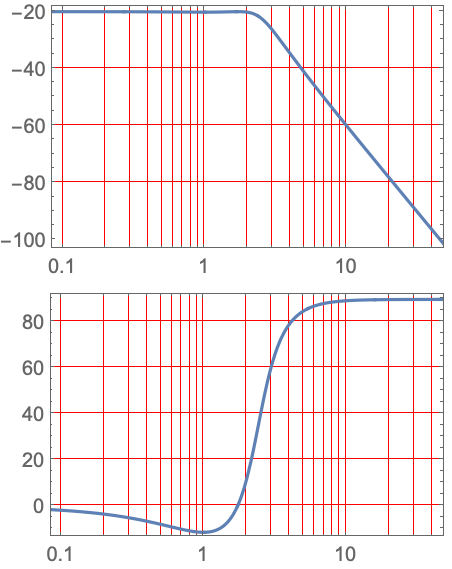
GridLines (3)
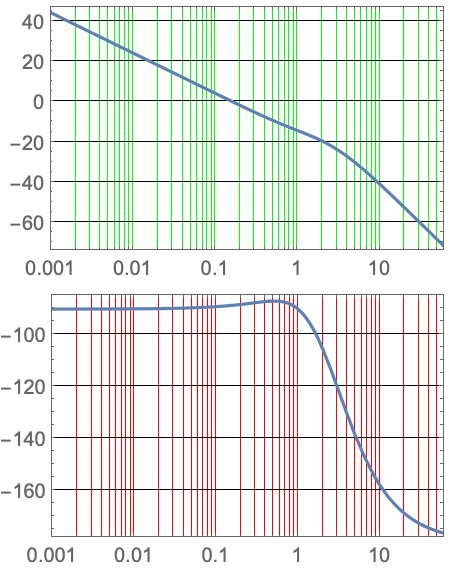
GridLinesStyle (2)
PhaseRange (1)
PlotLayout (1)
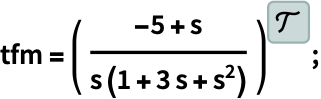
https://wolfram.com/xid/0i1r4wou6-xk6y4n
https://wolfram.com/xid/0i1r4wou6-nvn5il
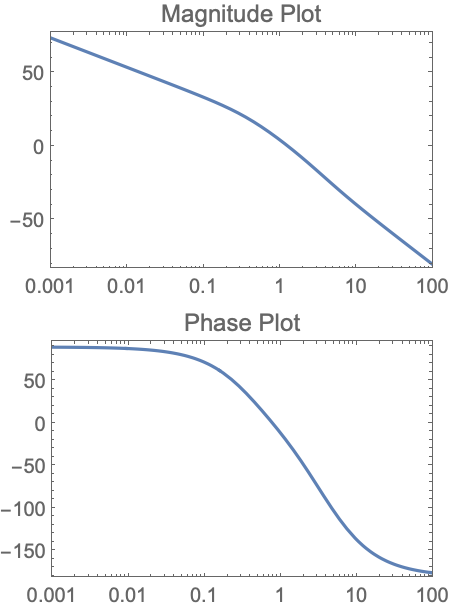
https://wolfram.com/xid/0i1r4wou6-81yth1
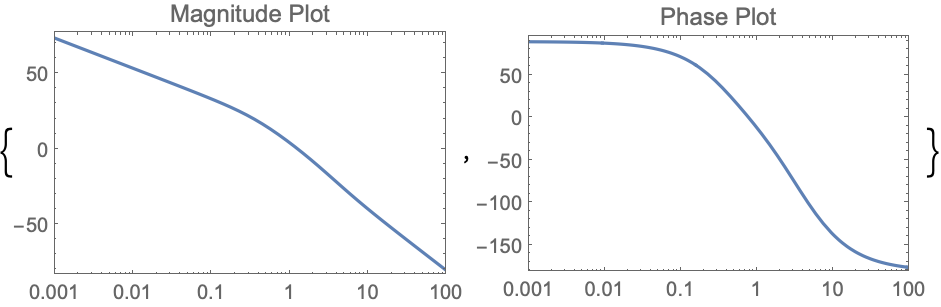
https://wolfram.com/xid/0i1r4wou6-3240je
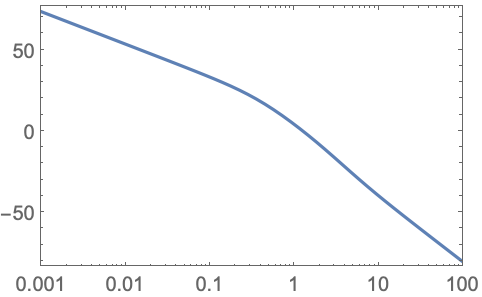
https://wolfram.com/xid/0i1r4wou6-6yf5w3
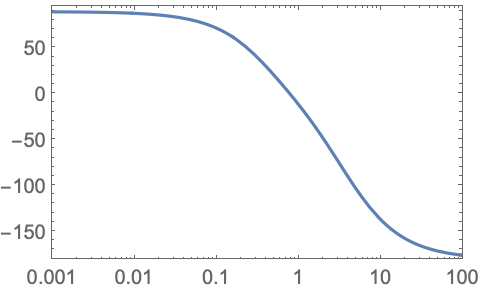
PlotTheme (2)
SamplingPeriod (2)
https://wolfram.com/xid/0i1r4wou6-cmen34
https://wolfram.com/xid/0i1r4wou6-b9ibpq
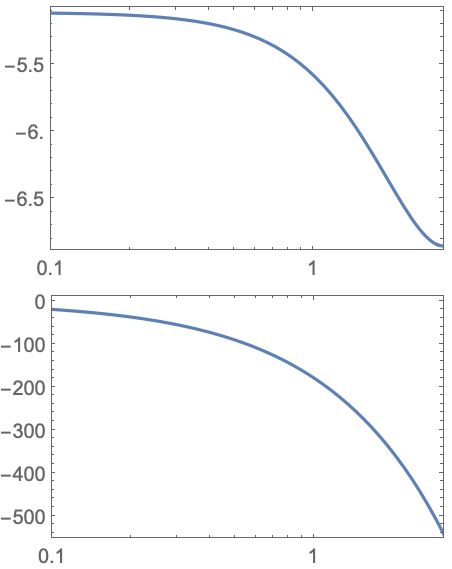
BodePlot関数でサンプリング周期を指定する:
https://wolfram.com/xid/0i1r4wou6-ubqqcz
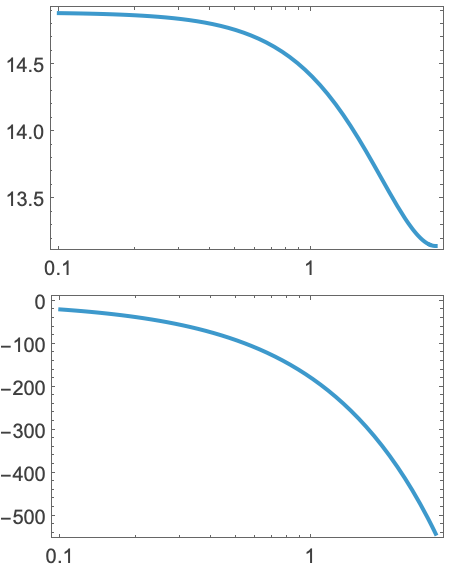
https://wolfram.com/xid/0i1r4wou6-gwhv09
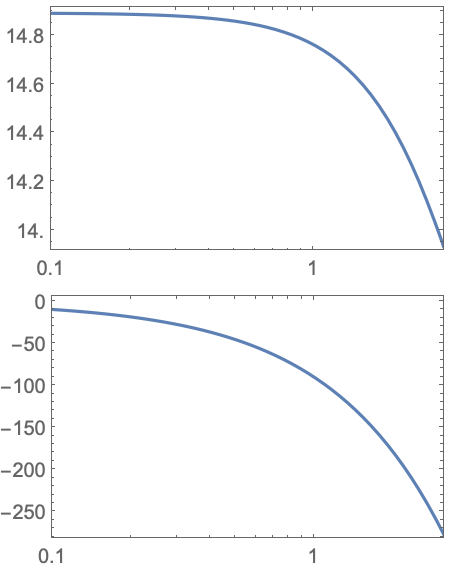
ScalingFunctions (2)
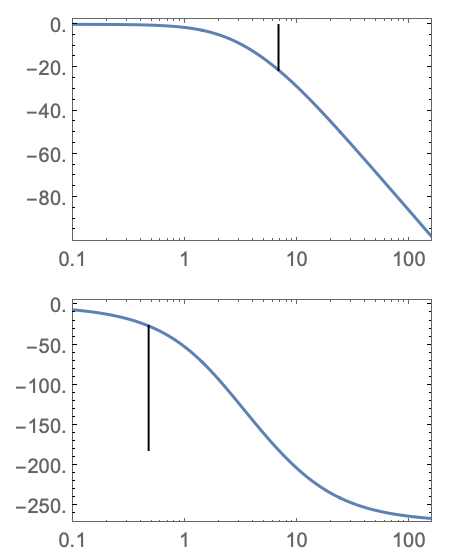
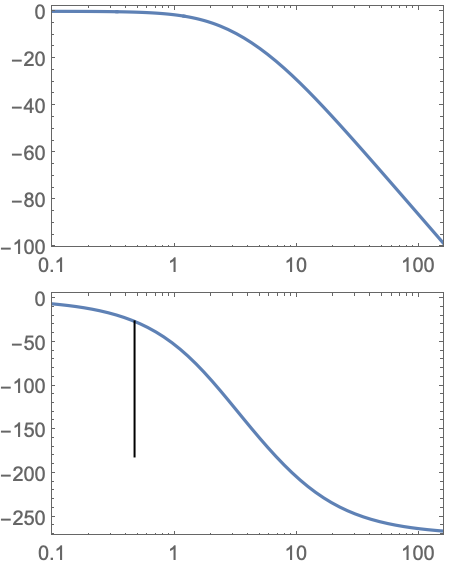
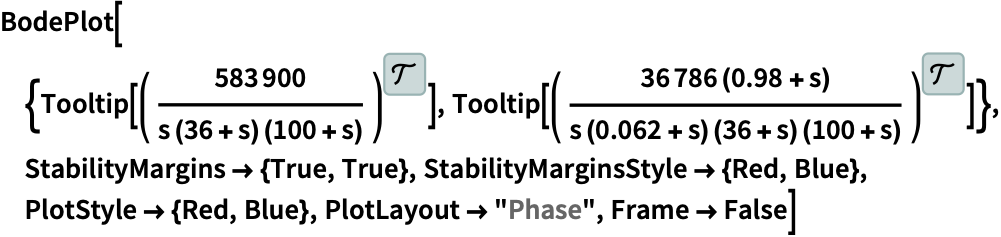
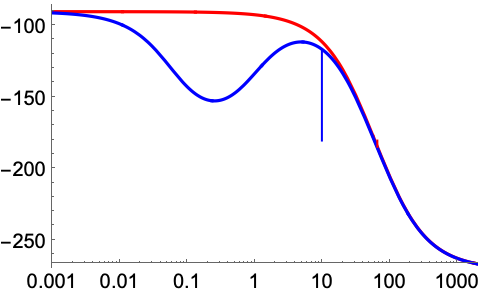
StabilityMargins (2)
アプリケーション (7)この関数で解くことのできる問題の例
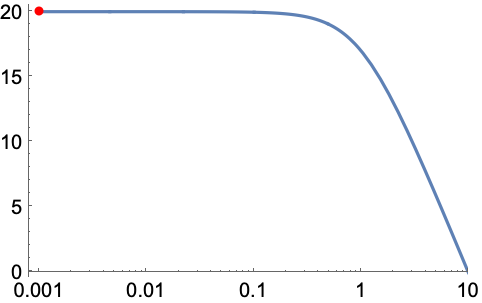
タイプ0系の静止位置誤差定数は定常状態におけるゲインである:

https://wolfram.com/xid/0i1r4wou6-7qov47

https://wolfram.com/xid/0i1r4wou6-42wtgo
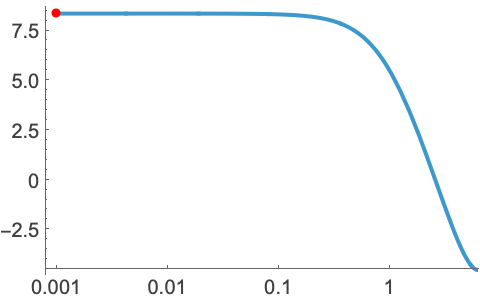
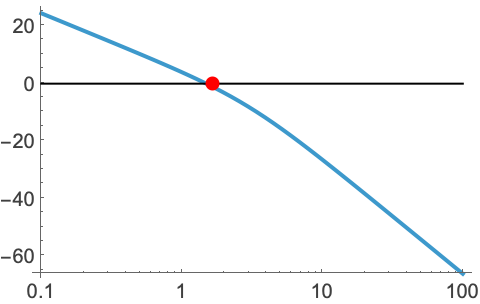
タイプ1系の静止速度誤差定数は0 dBラインと最初の10年における![]() デシベルのセグメント(あるいはその延長)のほぼ交点である:
デシベルのセグメント(あるいはその延長)のほぼ交点である:

https://wolfram.com/xid/0i1r4wou6-hm7wr7

https://wolfram.com/xid/0i1r4wou6-v3y4xp
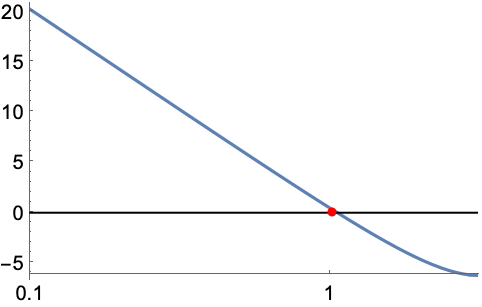
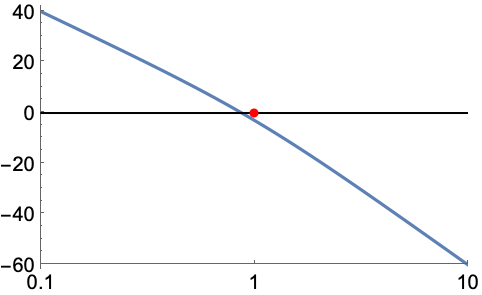
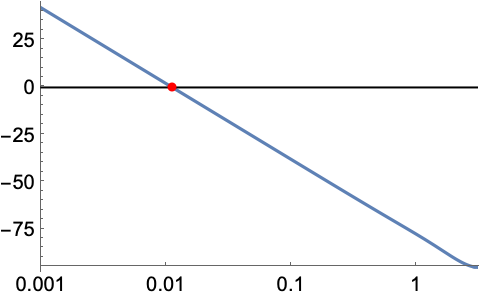
タイプ2の系の静止加速度誤差定数の平方根は最初の10年間に![]() デシベルのセグメント(あるいはその延長)と0 dB線とのほぼ交点である:
デシベルのセグメント(あるいはその延長)と0 dB線とのほぼ交点である:

https://wolfram.com/xid/0i1r4wou6-fmsud

https://wolfram.com/xid/0i1r4wou6-6jgffr
https://wolfram.com/xid/0i1r4wou6-obungf
サンプリング周期が1のゼロ次ホールドの周波数応答を可視化する:

https://wolfram.com/xid/0i1r4wou6-igqu0u
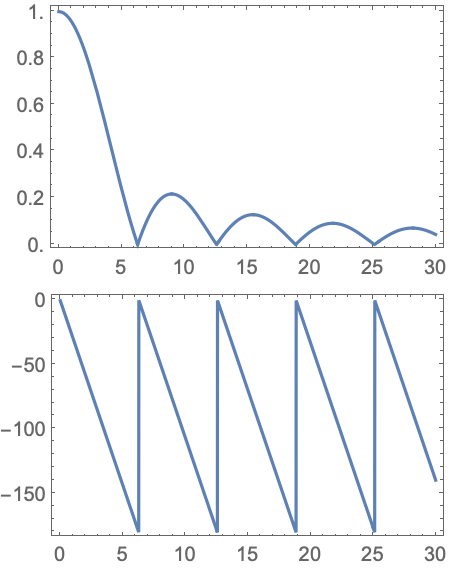
ラプラス変数がラジアン/秒のときに,周波数がヘルツのボード線図を得る:
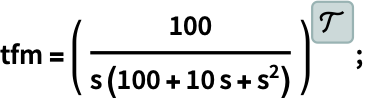
https://wolfram.com/xid/0i1r4wou6-zljn22
https://wolfram.com/xid/0i1r4wou6-bo9su3
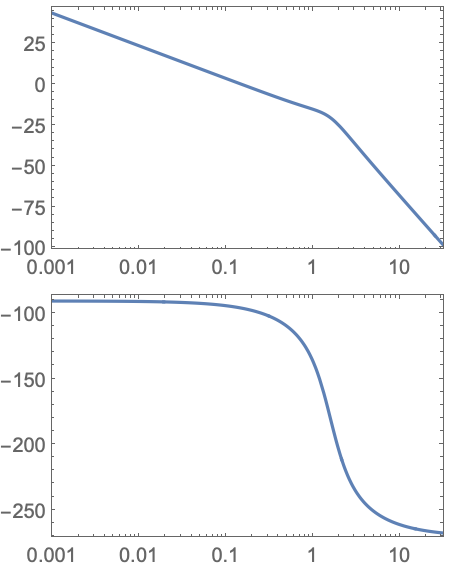
連続時間系については,ラプラス変数をスケールすることで,同じ結果を得ることができる:
https://wolfram.com/xid/0i1r4wou6-7p8sb1
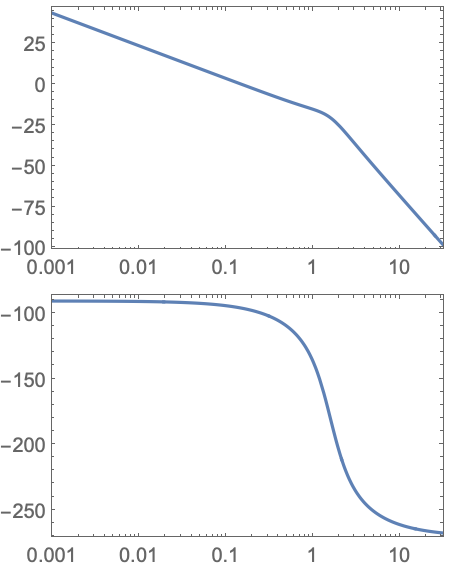
ラジアン/秒のZ変換変数による離散時間系についてのヘルツの点:
https://wolfram.com/xid/0i1r4wou6-dvbzsb
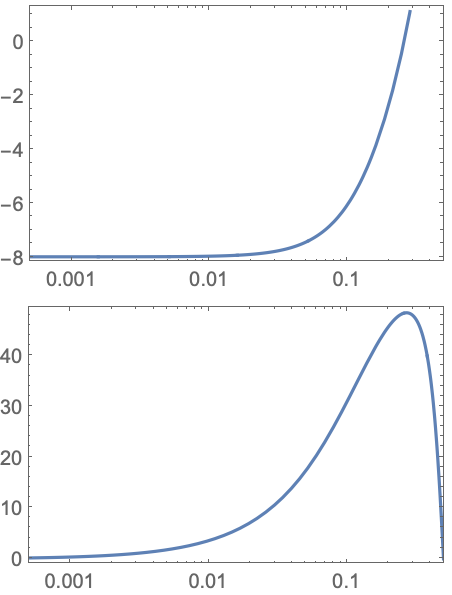
特性と関係 (1)この関数の特性および他の関数との関係
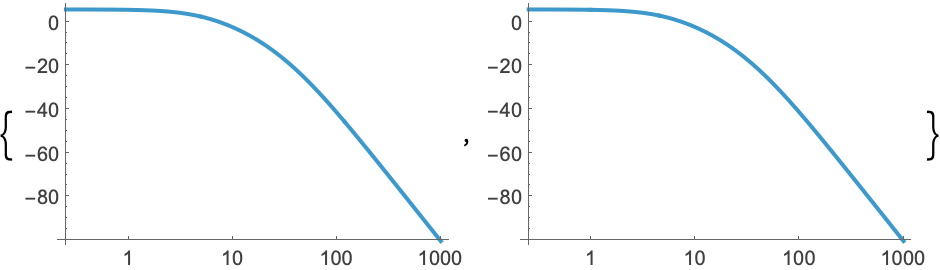
SingularValuePlotはボード線図のゲイン線図を多入力多出力系に一般化する:
https://wolfram.com/xid/0i1r4wou6-yhmful
https://wolfram.com/xid/0i1r4wou6-9f9yd4
Wolfram Research (2010), BodePlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/BodePlot.html (2014年に更新).テキスト
Wolfram Research (2010), BodePlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/BodePlot.html (2014年に更新).
Wolfram Research (2010), BodePlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/BodePlot.html (2014年に更新).CMS
Wolfram Language. 2010. "BodePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/BodePlot.html.
Wolfram Language. 2010. "BodePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/BodePlot.html.APA
Wolfram Language. (2010). BodePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BodePlot.html
Wolfram Language. (2010). BodePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BodePlot.htmlBibTeX
@misc{reference.wolfram_2025_bodeplot, author="Wolfram Research", title="{BodePlot}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/BodePlot.html}", note=[Accessed: 25-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_bodeplot, organization={Wolfram Research}, title={BodePlot}, year={2014}, url={https://reference.wolfram.com/language/ref/BodePlot.html}, note=[Accessed: 25-April-2025
]}