ComplexRegionPlot
ComplexRegionPlot[pred,{z,zmin,zmax}]
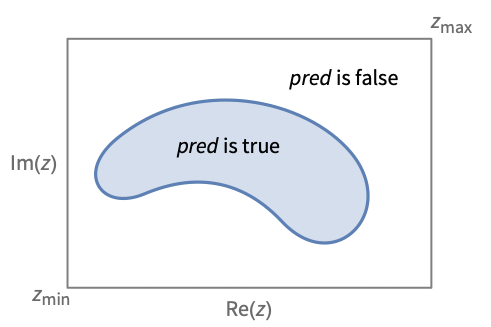
pred がTrueとなる複素平面上の領域を示すプロットを作成する.
ComplexRegionPlot[{pred1,pred2,…},{z,zmin,zmax}]
複数の述語 prediによって与えられた領域をプロットする.
詳細とオプション




- 述語 prediは不等式の任意の論理結合でよい.prediは,比較の目的で複素数から実数成分を抽出する,Re,Im,Abs,Argのような関数を含むことが多い.
- ComplexRegionPlotがプロットする領域には不連続の部分が含まれていてもよい.
- ComplexRegionPlot[pred,{z,n}]はComplexRegionPlot[pred,{z,-n-n I,n+n I}]と等価である.
- ComplexRegionPlotは,事実上Blockを使って,変数 z を局所的なものとして扱う.
- ComplexRegionPlotには属性HoldAllがあり,z に特定の数値を割り当てた後ではじめて pred を評価する.場合によっては,Evaluateを使ってまず pred を記号的に評価した方が効率的かもしれない.
- prediには次のラッパー w を使うことができる.
-
Annotation[predi,label] prediの注釈を与える Button[predi,action] prediの曲線がクリックされたときに action を評価する Callout[predi,label] コールアウトで領域にラベルを付ける Callout[predi,label,pos] コールアウトを相対的な位置 pos に置く EventHandler[predi,events] prediの一般的なイベントハンドラを定義する Hyperlink[predi,uri] 領域をハイパーリンクにする Labeled[predi,label] 領域にラベルを付ける Labeled[predi,label,pos] ラベルを相対的な位置 pos に置く Legended[predi,label] 領域を凡例で識別する PopupWindow[predi,cont] 領域にポップアップウィンドウを付ける StatusArea[predi,label] マウスオーバーの際にステータスエリアに表示する Style[predi,styles] 領域を指定のスタイルで表示する Tooltip[predi,label] 領域にツールチップを付ける Tooltip[predi] 領域をツールチップとして使う - ラッパー w は複数のレベルで適用できる.
-
w[predi] prediをラップする w[{predi,…}] prediの集合をラップする w1[w2[…]] ネストしたラッパーを使う - Callout,Labeled,Placedには次の位置 pos が使える.
-
Automatic 自動的に置かれたラベル Above, Below, Before, After 曲線の周囲の位置 z z 近くの位置 {pos,epos} 領域の相対的な位置 pos に置かれたラベル内の epos - ComplexRegionPlotにはGraphicsと同じオプションに以下の追加・変更を加えたものが設定できる. [全オプションのリスト]
-
AspectRatio 1 縦横比 BoundaryStyle Automatic 各領域の境界のスタイル ColorFunction Automatic 各領域の内側の彩色をどうするか ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか EvaluationMonitor None 各関数評価で評価される式 Frame True プロットの周囲に枠を描くかどうか LabelingSize Automatic コールアウトとラベルの最大サイズ MaxRecursion Automatic 許容される再帰分割の最大数 Mesh None メッシュラインを何本引くか MeshFunctions {#1&,#2&} どのようなメッシュラインを描くか MeshShading None メッシュライン間の領域の陰影付けをどうするか MeshStyle Automatic メッシュラインのスタイル Method Automatic 領域を細分化するためのメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotLabels None 曲線に使うラベル PlotLegends None 領域の凡例 PlotPoints Automatic サンプル点の初期数 PlotRange Full プロットに含める値の範囲 PlotRangeClipping True プロット範囲で切り取るかどうか PlotRangePadding Automatic 値の範囲をどの程度充填するか PlotStyle Automatic 領域のスタイルを指定するグラフィックス指示子 PlotTheme $PlotTheme プロットの全体的なテーマ TextureCoordinateFunction Automatic テクスチャ座標をどのように決めるか TextureCoordinateScaling True TextureCoordinateFunctionの引数をスケールするかどうか WorkingPrecision MachinePrecision 内部計算に使われる精度 - 次は,PlotLegendsのよく使われる設定である.
-
None 凡例は付けない Automatic 凡例を自動的に決定する "Expressions" f1, f2, … を凡例ラベルとして使う {lbl1,lbl2,…} lbl1, lbl2, … を凡例ラベルとして使う Placed[lspec,…] 凡例の置き方を指定する - ComplexRegionPlotは,まず,PlotPointsで指定された等間隔のサンプル点の格子で pred を評価する.次に,pred がTrueとなるすべての領域の境界を見付けるために,適応的アルゴリズムを使って最大でMaxRecursion回再分割する.
- 使うサンプル点の数が有限なので,pred がTrueとなる領域をComplexRegionPlotが見逃す可能性がある点に留意する必要がある.結果をチェックする際は,PlotPointsおよびMaxRecursionの設定を大きくするとよい.
- デフォルト設定のPlotRange->Fullのとき,ComplexRegionPlotは z の全範囲(zminから zmaxまで)を明示的に含む.
- ComplexRegionPlotは,一般に,正の領域のみを求める.線あるいは点のみの領域は求められない.
- MeshFunctions内の関数に渡される引数は z である.ColorFunctionとTextureCoordinateFunctionには,デフォルトで,Re[z],Im[z],Abs[z],Arg[z]のスケールされたバージョンが渡される.
全オプションのリスト



例題
すべて開くすべて閉じる例 (5)
スコープ (23)
サンプリング (3)
ラベルと凡例 (9)
Labeledで領域にラベルを付ける:
Calloutで領域にラベルを付ける:
ラベルが領域内にあるときはコールアウトのリーダー線は使われない:
PlotLegendsで凡例を加える:
Legendedで凡例を加える:
プレゼンテーション (11)
領域に明示的なPlotStyleを与える:
領域の境界に明示的なBoundaryStyleを与える:
オプション (59)
BoundaryStyle (4)
ColorFunction (5)
スケールされた,Re[z],Im[z],Abs[z]あるいはArg[z]で領域に彩色する:
名前付きの色関数はスケールされたArg[z]方向を使う:
ColorFunctionはPlotStyleより優先順位が高い:
ColorFunctionはMeshShadingより優先順位が低い:
Mesh (7)
MeshShading (4)
PlotLabels (5)
PlotLegends (8)
PlotStyle (5)
TextureCoordinateFunction (4)
アプリケーション (25)
基本的な形 (5)
高度な形 (2)
数学的恒等式 (1)
収束領域 (6)
複素領域のマッピング (7)
![]() 平面上の領域を,同じ大きさ,形,向きで量
平面上の領域を,同じ大きさ,形,向きで量 ![]() 分
分 ![]() 平面方向にシフトさせる加法関数
平面方向にシフトさせる加法関数 ![]() を定義する:
を定義する:
rect[f[z]]をプロットすると,rect[z]の原像が与えられる:
![]() 平面上の領域を同じ形の
平面上の領域を同じ形の ![]() 平面上の領域にスケールして回転させる線形関数
平面上の領域にスケールして回転させる線形関数 ![]() を定義する:
を定義する:
![]() 平面から
平面から ![]() 平面への倍率はAbs[c]で回転角はArg[c]である:
平面への倍率はAbs[c]で回転角はArg[c]である:
Abs[c]でスケーリングを,Arg[c]で回転を,![]() でシフトを組み合せるアフィン関数を定義する:
でシフトを組み合せるアフィン関数を定義する:
![]() 平面における境界の形を決定するために,
平面における境界の形を決定するために,![]() 平面における正方形の天辺について考える.ただし,
平面における正方形の天辺について考える.ただし,![]() (
(![]() )である.この辺が
)である.この辺が ![]() 平面の
平面の![]() を中心として半径が
を中心として半径が![]() の半円に相当することを示す:
の半円に相当することを示す:
線形分数変換円と線を円と線にマッピングする.この線形分数変換は上半平面を単位円板にマッピングする:
これは ![]() であることを示唆する.これはNestListで確かめられる:
であることを示唆する.これはNestListで確かめられる:
物理におけるアプリケーション (1)
特性と関係 (8)
ComplexRegionPlotはRegionPlotの特殊ケースである:
ComplexContourPlotは複素数上に曲線をプロットする:
ComplexPlotは関数の引数と大きさを色を使って示す:
ComplexPlot3Dを使って ![]() 軸を大きさに使う:
軸を大きさに使う:
複素数の配列にComplexArrayPlotを使う:
ReImPlotとAbsArgPlotを使って複素数値を実数上にプロットする:
ComplexListPlotを使って複素数の位置を平面上に示す:
ComplexStreamPlotとComplexVectorPlotは複素数を方向として扱う:
考えられる問題 (1)
RegionPlotは二次元領域しか可視化できない:
テキスト
Wolfram Research (2020), ComplexRegionPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/ComplexRegionPlot.html.
CMS
Wolfram Language. 2020. "ComplexRegionPlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ComplexRegionPlot.html.
APA
Wolfram Language. (2020). ComplexRegionPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ComplexRegionPlot.html