ComplexRegionPlot
ComplexRegionPlot[pred,{z,zmin,zmax}]
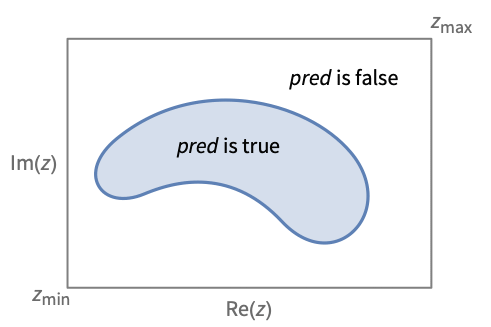
绘制复平面上 pred 为 True 的区域.
ComplexRegionPlot[{pred1,pred2,…},{z,zmin,zmax}]
绘制由多个谓词 predi 给定的区域.
更多信息和选项




- 谓词 predi 可为为任意不等式的逻辑组合. predi 通常会涉及如 Re、Im、Abs 和 Arg 这样的函数,从复数中提取实数以进行比较.
- ComplexRegionPlot 绘制的区域可包含不相连的部分.
- ComplexRegionPlot[pred,{z,n}] 等价于 ComplexRegionPlot[pred,{z,-n-n I,n+n I}].
- ComplexRegionPlot 将变量 z 视为局部变量,相当于使用 Block.
- ComplexRegionPlot 具有属性 HoldAll,只在对 z 赋值后才计算 pred. 某些情况下,先用 Evaluate 对 pred 进行符号式计算效率更高.
- 以下封装 w 可用于 predi:
-
Annotation[predi,label] 为 predi 提供注释 Button[predi,action] 当 predi 的曲线被点击时执行 action Callout[predi,label] 用标注 (callout) 标记区域 Callout[predi,label,pos] 将标注放置在相对位置 pos EventHandler[predi,events] 定义 predi 的通用事件处理程序 Hyperlink[predi,uri] 把区域变为一个超链接 Labeled[predi,label] 标记区域 Labeled[predi,label,pos] 将标签放置在相对位置 pos Legended[predi,label] 在图例中标识区域 PopupWindow[predi,cont] 为区域添加弹出窗口 StatusArea[predi,label] 当鼠标移过时在状态栏中显示 Style[predi,styles] 用指定样式显示区域 Tooltip[predi,label] 为区域添加提示条 Tooltip[predi] 将区域用作提示条 - 可在多个层级上应用封装 w:
-
w[predi] 封装 predi w[{predi,…}] 封装一组 predi w1[w2[…]] 使用嵌套封装 - Callout、Labeled 和 Placed 可使用以下位置 pos:
-
Automatic 自动放置标签 Above, Below, Before, After 区域周围的位置 z z 附近的位置 {pos,epos} 在区域的相对位置 pos 处放置的标签中的 epos - ComplexRegionPlot 和 Graphics 有相同的选项,不同之处和更多选项如下所示: [所有选项的列表]
-
AspectRatio 1 高宽比 BoundaryStyle Automatic 每个区域的边界的样式 ColorFunction Automatic 怎样为每个区域的内部着色 ColorFunctionScaling True 是否对 ColorFunction 的参数进行缩放 EvaluationMonitor None 每次运行函数时要计算的表达式 Frame True 是否为图形绘制边框 LabelingSize Automatic 最大化标注和标签的大小 MaxRecursion Automatic 递归子划分的最大数量 Mesh None 绘制多少条网格线 MeshFunctions {#1&,#2&} 绘制什么样的网格线 MeshShading None 怎样处理网格线之间区域的色调 MeshStyle Automatic 网格线的样式 Method Automatic 细化区域所用的方法 PerformanceGoal $PerformanceGoal 优化的目标 PlotLabels None 曲线的标签 PlotLegends None 区域的图例 PlotPoints Automatic 初始采样点的个数 PlotRange Full 绘图中要包含的值的范围 PlotRangeClipping True 在绘图范围边界处是否进行剪切 PlotRangePadding Automatic 对值的范围进行多少填充 PlotStyle Automatic 指定区域的样式的图形指令 PlotTheme $PlotTheme 绘图的整体外观主题 TextureCoordinateFunction Automatic 怎样确定纹理的坐标 TextureCoordinateScaling True 是否对 TextureCoordinateFunction 的参数进行缩放 WorkingPrecision MachinePrecision 内部计算使用的精度 - PlotLegends 的常见设置有:
-
None 没有图例 Automatic 自动确定图例 "Expressions" 用 f1、f2、… 作为图例标签 {lbl1,lbl2,…} 用 lbl1、lbl2、… 作为图例标签 Placed[lspec,…] 指定图例的放置 - ComplexRegionPlot 首先在由 PlotPoints 指定的等间隔采样点组成的网格上计算 pred. 然后使用一种自适应算法进行至多 MaxRecursion 次子划分,试图找出所有 pred 为 True 的区域的边界.
- 应该认识到由于使用的采样点数量有限,ComplexRegionPlot 可能会丢失某些 pred 为 True 的区域. 为确保结果正确,可以尝试增大 PlotPoints 和 MaxRecursion 的设置.
- 采用默认设置 PlotRange->Full 时,ComplexRegionPlot 将明确包含 z 从 zmin 到 zmax 内的所有值.
- ComplexRegionPlot 通常只能找到值为真的区域;找不到仅为线或点的区域.
- 为 MeshFunctions 中的函数提供的参数为 z. 默认情况下,为 ColorFunction 和 TextureCoordinateFunction 提供的是 Re[z]、Im[z]、Abs[z]、Arg[z] 经过缩放的值.
所有选项的列表




范例
打开所有单元关闭所有单元范围 (23)
采样 (3)
添加标签和图例 (9)
演示 (11)
为区域设置明确的 PlotStyle:
为区域的边界设置明确的 BoundaryStyle:
选项 (59)
BoundaryStyle (4)
ColorFunction (5)
用缩放过的 Re[z]、Im[z]、Abs[z] 或 Arg[z] 为区域着色:
已命名颜色函数沿缩放过的 Arg[z] 方向进行着色:
ColorFunction 比 PlotStyle 的优先级高:
ColorFunction 比 MeshShading 的优先级低:
Mesh (7)
MeshShading (4)
PlotLabels (5)
PlotLegends (8)
PlotStyle (5)
TextureCoordinateFunction (4)
应用 (25)
基本形状 (5)
收敛区域 (6)
映射复区域 (7)
定义一个加性函数 ![]() ,将
,将 ![]() 平面的区域移动
平面的区域移动 ![]() ,移至
,移至 ![]() 平面中,并保持大小、形状和方位不变:
平面中,并保持大小、形状和方位不变:
如果绘制 rect[f[z]],可获得 rect[z] 的预映射:
定义一个线性函数 ![]() ,将
,将 ![]() 平面上的区域缩放和旋转至
平面上的区域缩放和旋转至 ![]() 平面,保持形状不变:
平面,保持形状不变:
从 ![]() 平面到
平面到 ![]() 平面的缩放因子为 Abs[c],旋转角度为 Arg[c]:
平面的缩放因子为 Abs[c],旋转角度为 Arg[c]:
定义一个仿射函数,将缩放 Abs[c]、旋转 Arg[c] 和平移 ![]() 组合在一起:
组合在一起:
为了确定 ![]() 平面中边界的形状,考虑
平面中边界的形状,考虑 ![]() 平面中正方形的上边缘,即
平面中正方形的上边缘,即 ![]() ,
,![]() ,显示它对应于
,显示它对应于 ![]() 平面中以
平面中以 ![]() 为圆心,半径为
为圆心,半径为 ![]() 的半圆:
的半圆:
线性分式变换以将圆和线映射到圆和线著名. 下面的线性分式变换将上半平面映射到单位圆盘:
这说明 ![]() ,可通过 NestList 来确认这一点:
,可通过 NestList 来确认这一点:
物理应用 (1)
属性和关系 (8)
ComplexRegionPlot 是 RegionPlot 的特例:
ComplexContourPlot 在复平面上绘制曲线:
ComplexPlot 用颜色显示函数的辐角和大小:
通过 ComplexPlot3D 用 ![]() 轴显示幅值:
轴显示幅值:
用 ComplexArrayPlot 绘制复数数组:
用 ReImPlot 和 AbsArgPlot 在实平面上绘制复数:
用 ComplexListPlot 显示复数在平面上的位置:
ComplexStreamPlot 和 ComplexVectorPlot 将复数视为方向:
可能存在的问题 (1)
RegionPlot 只可视化二维区域:
文本
Wolfram Research (2020),ComplexRegionPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexRegionPlot.html.
CMS
Wolfram 语言. 2020. "ComplexRegionPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ComplexRegionPlot.html.
APA
Wolfram 语言. (2020). ComplexRegionPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ComplexRegionPlot.html 年