DSolve
更多信息和选项


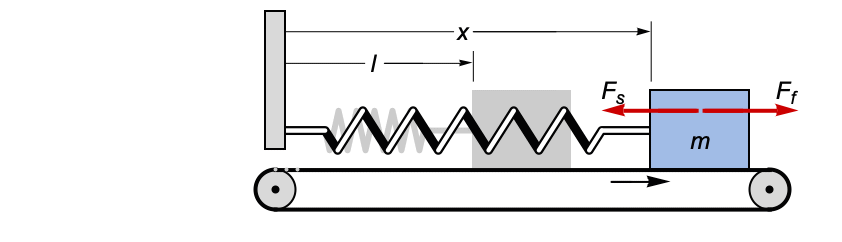
- DSolve 可以求解常微分方程 (ODE)、偏微分方程 (PDE)、微分代数方程 (DAE)、 时滞微分方程 (DDE)、积分方程、积分微分方程以及混合型微分方程.
- 可用 DSolve 求解的不同的方程类型包括:
-
u'[x]f[x,u[x]] 常微分方程 a ∂xu[x,y]+b ∂yu[x,y]f 偏微分方程 f[u'[x],u[x],x]0 微分代数方程 u'[x]f[x,u[x-x1]] 时滞微分方程 u'[x]+ 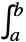 k[x,t]u[t]tf
k[x,t]u[t]tf积分微分方程 {…,WhenEvent[cond,u[x]g]} 混合型微分方程 - DSolve 的输出由关联函数 u 或 u[x] 的形式控制:
-
DSolve[eqn,u,x] {{uf},…} 其中 f 为纯函数 DSolve[eqn,u[x],x] {{u[x]f[x]},…} 其中 f[x] 是关于 x 的表达式 - 如果输出为纯函数,可用 eqn/.{{uf},…} 验证解的正确性. »
- DSolve[eqn] 中的因变量是从 eqn 中推导出来的,可以明确指定为 u[x],也可以指定为自变量方程的纯函数 u. »
- DSolve 有时会以 Solve 的形式给出隐式解. »
- DSolve 的解可能含有不能明确计算结果的 Inactive 和与积分. 这种情况下,可使用变量 K[1]、K[2], …
- 可以通过给出在特定点的方程,比如 u[x1]a、u'[x2]b 等等,指定常微分方程 (ODE) 和微分代数方程 (DAE) 的边界条件.
- 可以用方程 u[x,y1]a、Derivative[1,0][u][x,y1]b 等给出偏微分方程 (PDE) 的边界条件,或是以 DirichletCondition[u[x,y]g[x,y],cond] 形式给出.
- 可以利用历史函数 g[x],以 u[x/;x<x0]g[x] 形式给出时滞微分方程 (DDE) 的初始条件.
- 还可以将 WhenEvent[event,action] 包含在方程 eqn 中,用来指定当 event 变成 True 时采取的 action.
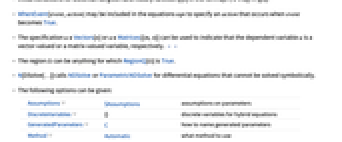
- 规约 u∈Vectors[n] 或 u∈Matrices[{m,n}] 可用于分别表示因变量 u 是向量值变量或矩阵值变量.或者将 u 定义为 VectorSymbol 或 MatrixSymbol. » »
- Ω 可以是任何令 RegionQ[Ω] 为 True 的区域.
- 对于不能进行符号式求解的微分方程,N[DSolve[…]] 会调用 NDSolve 或 ParametricNDSolve.
- 可以给出下列选项:
-
Assumptions $Assumptions 对参数的假设 DiscreteVariables {} 混合型方程的离散变量 GeneratedParameters C 怎样命名产生的参数 Method Automatic 使用什么方法 IncludeSingularSolutions False 是否包括奇异解 - GeneratedParameters 控制产生参数的形式;缺省情况下,对于常微分方程 (ODE) 和微分代数方程 (DAE),这些参数是常数 C[n],对于偏微分方程 (PDE),则为任意函数 C[n][…]. »
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (117)
线性微分方程 (6)
非线性微分方程 (6)
微分方程组 (8)
或者将 ![]() 定义为 VectorSymbol:
定义为 VectorSymbol:
或者将 ![]() 定义为 MatrixSymbol:
定义为 MatrixSymbol:
分段微分方程 (4)
混合微分方程 (8)
Sturm-Liouville 问题 (6)
利用 Assumptions 获取位于该范围内的特征函数:
积分方程 (6)
一阶偏微分方程 (7)
对任意函数 C[1] 作特定选择后的解:
椭圆型偏微分方程 (9)
一般偏微分方程 (6)
无论四个常数 C[k] 取何值,ψ 都满足方程及边界条件:
区域上的偏微分方程 (3)
从 Inactive 和中提取前 100 项:
分数阶微分方程 (8)
求解包含 0.7 阶 CaputoD 的分数微分方程:
选项 (7)
Assumptions (2)
GeneratedParameters (2)
Method (1)
获取以 DifferentialRoot 形式给出的解:
SingularSolutions (1)
使用 IncludeSingularSolutions 可计算奇异解和一般解:
应用 (36)
常微分方程 (12)
混合微分方程 (8)
积分方程 (4)
等时降落问题要求找到一条向下的曲线,把珠子放在曲线任一位置,滑落到底的时间都相等. 把总的下降时间用曲线长度和速度 v 表示后,可以导出阿贝尔积分方程 ![]() . 通过关系
. 通过关系 ![]() 定义未知函数
定义未知函数 ![]() 并使用能量守恒方程
并使用能量守恒方程 ![]() 导出显式方程:
导出显式方程:
用 DSolve 求解积分方程:
让曲线从原点开始并积分——并假设被积函数是实数值的——导出以 ![]() 为自变量的函数
为自变量的函数 ![]() :
:
代换 ![]() 和
和 ![]() 的值,用 ParametricPlot 显示极大等时降线:
的值,用 ParametricPlot 显示极大等时降线:
变量替换 ![]() 可以给出一个简单的、非奇异的曲线参数化形式,范围在
可以给出一个简单的、非奇异的曲线参数化形式,范围在 ![]() 之间:
之间:
结合能量守恒方程和链式法则 ![]() 可以得出下列以
可以得出下列以 ![]() 为自变量的函数
为自变量的函数 ![]() 的微分方程:
的微分方程:
用 DSolve 求解积分微分方程:
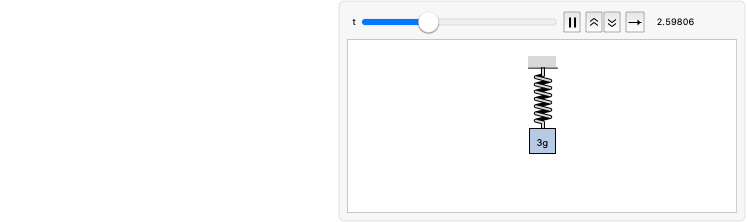
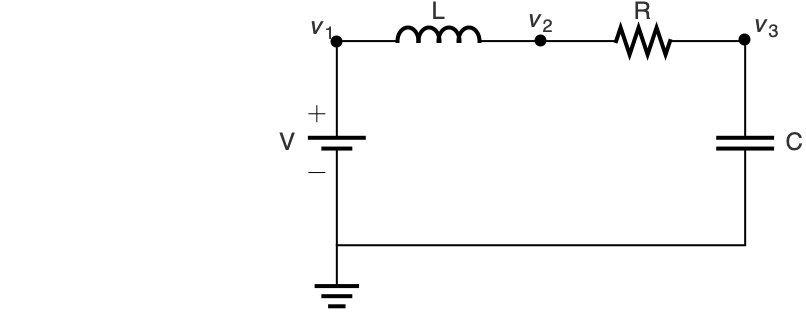
一个 LRC 电路,电压源为 ![]() . 电路的电阻是 0.2
. 电路的电阻是 0.2 ![]() ,电感是
,电感是
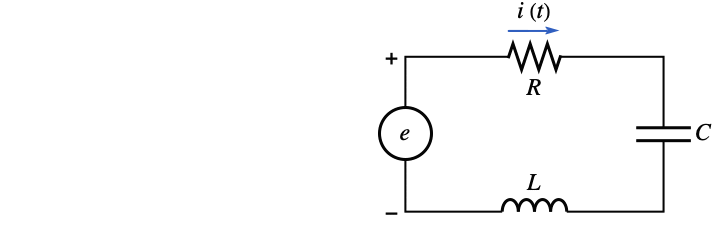
用 DSolve 求解积分微分方程:
一个线性沃尔泰拉积分方程等价于一个线性微分方程的初值问题. 为下列沃尔泰拉方程验证这个关系:
用 DSolve 求解积分方程:
经典偏微分方程 (5)
一般偏微分方程 (5)
研究当粘性参数变成无限小的极限情况下,伯格斯方程对冲击波的平滑解的演变情况:
一个被限制在长度为 d 的一位盒上移动的电子遵守端点处狄利克雷条件下的自由薛定谔方程:
和中的每一项被称为定态,因为用正弦函数作为初始条件会使位置概率密度 ![]() 与时间无关. 例如:
与时间无关. 例如:
将初始数据归一化,以使密度的积分(在某处发现粒子的总概率)为 1:
任意其它初始条件,即便简单到只是两个定态的和,都会导致产生复杂的含时密度:
用国际单位制中的单位输入电子的质量和 ![]() 的值,并将 d 设为典型的原子间距离,1 纳米,得到下列密度函数:
的值,并将 d 设为典型的原子间距离,1 纳米,得到下列密度函数:
将图像作成概率密度电影,可以看出电子的“中心”在盒子两个边之间来回移动:
求一份欧洲香草看涨期权的极值,如果如果标的资产价格与行权价格均为 $100,无风险利率为 5%,标的资产波动率为 20%,而到期期限为 1 年,使用布莱克–舒尔斯模型:
与 FinancialDerivative 给出的值相比较:
属性和关系 (10)
对应于 Integrate 的微分方程:
用 NDSolve 求数值解:
用 DEigensystem 求特征值和特征函数:
用 DSolve 计算脉冲响应:
用 InverseLaplaceTransform 执行同一计算:
DSolve 返回解的规则:
DSolveValue 返回解的表达式:
当符号解失败时,应用 N[DSolve[...]] 以调用 NDSolve:
使用 DFixedPoints 查找两个 ODE 方程组的定点:
使用 DStabilityConditions 来分析定点的稳定性:
可能存在的问题 (9)
结果可能包含未激活积分(inactive integral):
使用 Activate 运算积分:
这里,DSolve 给出错误信息,因为 ![]() 未被包括在第二个参数中:
未被包括在第二个参数中:
另外,也可使用 DSolveValue 来只获得 ![]() 的解:
的解:
此范例返回未计算值,因为 DSolve 无法将其解释为向量方程:
CompleteIntegral 求非线性偏微分方程的完全积分:
DSolve 返回相同解,但会带有警告信息:
用 CompleteIntegral 求线性偏微分方程的完全积分:
DSolve 返回此偏微分方程的通解:
技术笔记
历史
1991年引入 (2.0) | 在以下年份被更新:1996 (3.0) ▪ 2003 (5.0) ▪ 2014 (10.0) ▪ 2015 (10.3) ▪ 2016 (11.0) ▪ 2019 (12.0) ▪ 2021 (13.0) ▪ 2022 (13.1) ▪ 2022 (13.2) ▪ 2024 (14.1) ▪ 2025 (14.2)
文本
Wolfram Research (1991),DSolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DSolve.html (更新于 2025 年).
CMS
Wolfram 语言. 1991. "DSolve." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/DSolve.html.
APA
Wolfram 语言. (1991). DSolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DSolve.html 年
BibTeX
@misc{reference.wolfram_2025_dsolve, author="Wolfram Research", title="{DSolve}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/DSolve.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_dsolve, organization={Wolfram Research}, title={DSolve}, year={2025}, url={https://reference.wolfram.com/language/ref/DSolve.html}, note=[Accessed: 28-February-2026]}