ListSliceDensityPlot3D

ListSliceDensityPlot3D[farr,surf]

曲面 surf についてスライスされた値の三次元 farr の密度プロットを生成する．

ListSliceDensityPlot3D[{{x1,y1,z1,f1},{x2,y2,z2,f2},…},surf]

点{xi,yi,zi}における fiの値についてのスライス密度プロットを生成する．

ListSliceDensityPlot3D[…,{surf1,surf2,…}]

複数のスライス surf1, surf2, …上でスライス密度プロットを生成する．

詳細とオプション

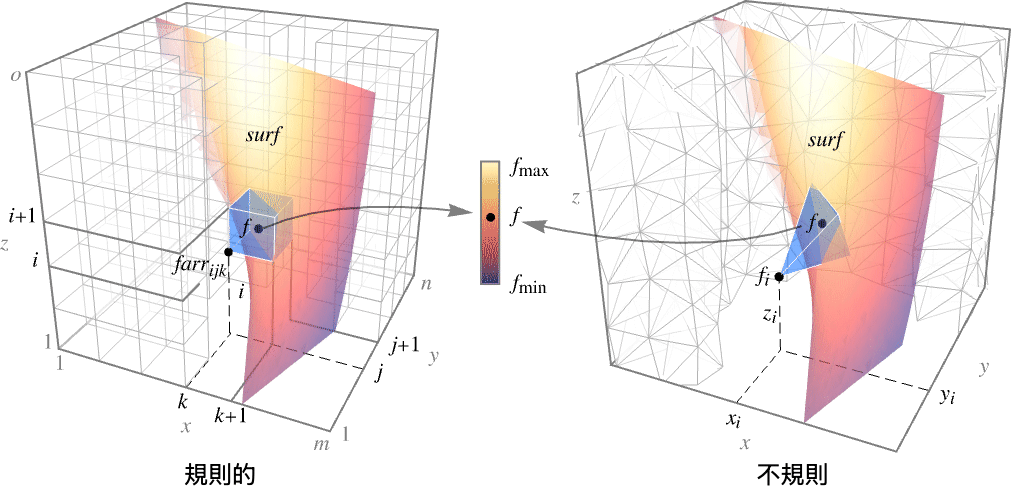
  • ListSliceDensityPlot3Dは補間された関数 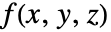を評価し，値を色にマップする．
  • 規則的なデータについては，関数 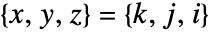は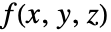で値 farr[[i,j,k]]を持つ．
  • 不規則データについて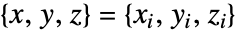は，は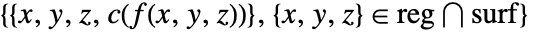で値 fiを持つ．
  • プロットは集合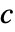を可視化する．ただし 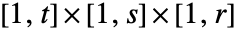は色関数で領域 reg は規則的なデータについてはデカルト積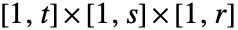，不規則データについては{{x1,y1,z1},…,{xn,yn,zn}}の凸包である．
  • 次の基本的なスライス面 surfiを与えることができる．
  • Automaticスライス面を自動的に決定する
    "CenterPlanes"中心を通る座標平面
    "BackPlanes"プロットの後ろの座標平面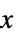
    "XStackedPlanes" 軸に沿って積み重ねられた座標平面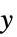
    "YStackedPlanes" 軸に沿って積み重ねられた座標平面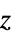
    "ZStackedPlanes" 軸に沿って積み重ねられた座標平面
    "DiagonalStackedPlanes"対角上に軸に沿って積み重ねられた座標平面
    "CenterSphere"中心の球
    "CenterCutSphere"切り取られたウェッジがある球
    "CenterCutBox"切り取られた象限があるボックス
  • ListSliceDensityPlot3D[data]はListSliceDensityPlot3D[data,Automatic]に等しい．
  • 基本的なスライス面には次のパラメータ化を使うことができる．
  • {"XStackedPlanes",n},n 個の等間隔の平面を生成
    {"XStackedPlanes",{x1,x2,…}}x=xiについての平面を生成
    {"CenterCutSphere",ϕopen}視点に面したカット角 ϕopen
    {"CenterCutSphere",ϕopen,ϕcenter} 平面上の中心角が ϕcenterのカット角 ϕopen
  • "YStackedPlanes"および"ZStackedPlanes"は"XStackedPlanes"についての指定に従う．追加的な特徴はスコープの例で示す．
  • 次の一般的なスライス面 surfiを使うことができる．
  • surfaceregion3Dにおける二次元領域，例：Hyperplane
    volumeregionsurfiが境界面とみなされる3Dにおける三次元領域，例：Cuboid
  • スライス面 surfiには次のラッパーを使うことができる．
  • Annotation[surf,label]注釈を与える
    Button[surf,action]曲面がクリックされた際に実行する動作を定義
    EventHandler[surf,…]曲面の一般的なイベントハンドラを定義
    Hyperlink[surf,uri]曲面がハイパーリンクとして動作するようにする
    PopupWindow[surf,cont]曲面にポップアップウィンドウを付ける
    StatusArea[surf,label]曲面上にマウスが来た場合にステータスエリアに表示
    Tooltip[surf,label]曲面に任意のツールチップを付ける
  • ListSliceDensityPlot3Dには，Graphics3Dと同じオプションに以下の追加・変更を加えたものが使える． [全オプションのリスト]
  • AxesTrue軸を描くかどうか
    BoundaryStyle Automatic表面の境界をどのようにスタイル付けするか
    BoxRatios {1,1,1}3D境界ボックスの比
    ClippingStyle NonePlotRangeで切り取られた値をどのように描くか
    ColorFunction Automaticプロットにどのように彩色するか
    ColorFunctionScaling TrueColorFunctionの引数をスケールするかどうか
    DataRange Automaticデータとして仮定する x，y，z の値の範囲
    PerformanceGoal $PerformanceGoalパフォーマンスのどの面について最適化するか
    PlotLegends None色勾配の凡例
    PlotPoints Automatic各方向のスライス面 surfiの近似サンプル数
    PlotRange {Full,Full,Full,Automatic}含める f あるいはその他の値の範囲
    PlotTheme $PlotThemeプロットの全体的なテーマ
    RegionFunction (True&)点を含めるかどうかをどのように決定するか
    ScalingFunctions None個々の座標のスケール方法
    TargetUnits Automatic使用する所望の単位
  • ColorFunctionには，デフォルトで，f のスケールされた値が渡される．
  • RegionFunctionには，デフォルトで，x，y，z，f が渡される．
  • 次元{r,s,t}の farr については，設定DataRangeAutomaticはDataRange{{1,r},{1,s},{1,t}}に等しい．
  • 次は，ScalingFunctionsの可能な設定である．
  • sff 密度の値をスケールする
    {sx,sy,sz}x，y， z の各軸をスケールする
    {sx,sy,sz,sf}x，y， z の各軸と f 密度の値をスケールする
  • 次は，よく使われる組込みのスケーリング関数 s である．
  • "Log"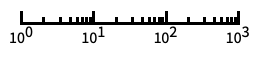自動的に目盛ラベルを付ける対数スケール
    "Log10"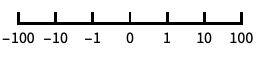10のベキ乗に目盛を置く，10を底とした対数スケール
    "SignedLog"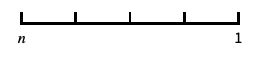0と負の数を含む対数に似たスケール
    "Reverse"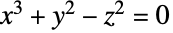座標の向きを逆にする

    • 全オプションのリスト

例題

すべて開くすべて閉じる

例  (2)

表面の集合上に値の配列の密度をプロットする：

値の配列についての密度を曲面 上にプロットする：

スコープ  (24)

表面  (9)

標準的なスライス面上に密度プロットを生成する：

標準的な軸と並んだ積み重ねスライス面：

標準的な境界表面：

半平面上に密度をプロットする：

体積プリミティブ上にプロットすることは，RegionBoundary[reg]上にプロットすることに等しい：

曲面 上に密度をプロットする：

複数の表面上に密度をプロットする：

積み重ね平面の数を指定する：

中心切取り球スライスについての切取り角を指定する：

データ  (8)

個の値からなる規則的なデータについては，，， データは配列中のその位値を反映する：

DataRangeを使って明示的な ，， データ範囲を与える：

(, , , )のタプルからなる不規則データからの補間密度をプロットする：

データの値が与えられた点を示す：

SparseArrayで与えられた値の配列について，密度をプロットする：

QuantityArrayで与えられた値の配列について，密度をプロットする：

PlotPointsを使ってスライス面の適応的サンプリングを制御する：

RegionFunctionを使って不明瞭なスライスを露出させる：

プロットの x 軸をスケールする：

z 軸の向きを逆にする：

プレゼンテーション  (7)

PlotThemeを使って全体的なスタイリングを即座に得る：

PlotLegendsを使って異なる値についての色の棒を得る：

Axesで軸の表示を制御する：

AxesLabelを使って軸に，PlotLabelを使ってプロット全体にラベルを付ける：

ColorFunctionで関数の値でプロットに色付けする：

BoundaryStyleでスライス面の境界にスタイルを付ける：

TargetUnitsは，可視化でどの単位を使うかを指定する：

オプション  (33)

BoundaryStyle  (1)

スライス面の境界にスタイルを付ける：

BoxRatios  (3)

デフォルトでは，境界ボックスの辺は同じ長さである：

BoxRatios->Automaticを使って3D座標値の自然なスケールを示す：

境界ボックスの各側にカスタムの長さ比を使う：

ClippingStyle  (2)

切り取られた領域に彩色する：

Noneを使って切り取られた領域を取り除く：

ColorFunction  (3)

の値に従ってスライス面に色付けする：

ColorDataで使用可能な名前付きの色勾配を使う：

のところに赤を使う：

ColorFunctionScaling  (2)

デフォルトで，スケールされた値が使われる：

ColorFunctionScaling->Falseを使ってスケールされていない f の値にアクセスする：

DataRange  (2)

デフォルトで，データ範囲は配列の次元であるとみなされる：

データ範囲を明示的に指定する：

PerformanceGoal  (2)

より品質の高いプロットを生成する：

品質を犠牲にしてもパフォーマンスを優先する：

PlotLegends  (3)

密度の凡例を示す：

PlotLegendsは自動的に色関数をマッチさせる：

Placedで凡例の配置を制御する：

PlotPoints  (1)

PlotPointsを使ってスライス面のサンプリングを決定する：

PlotRange  (3)

デフォルトで，全(All)密度が示される：

選択範囲を示す：

の値を含む選択された範囲を示す：

PlotTheme  (3)

詳しい格子線，目盛，凡例のテーマを使う：

明示的にオプションを設定してPlotThemeスタイルを無効にする：

さまざまなプロットテーマを比較する：

RegionFunction  (2)

あるいは の密度のみを含める：

となる部分の等高線のみを含める：

ScalingFunctions  (5)

デフォルトで，プロットのすべての方向が線形スケールになる：

軸が対数スケールのプロットを作成する：

ScalingFunctionsを使って 軸の方向が逆になるようにスケールする：

関数とその逆関数によって定義されたスケールを使う：

スケーリング関数は変数によって定義されたスライスに適用される：

名前付きのスライス表面はスケーリング関数によっては変形されない：

TargetUnits  (1)

QuantityArrayで指定された単位はTargetUnitsで指定された単位に変換される：

アプリケーション  (9)

基本データ  (4)

で生成されるデータの密度スライスをプロットする：

球上の および から生成されたデータの密度：

および から生成されたデータ：

および から生成されたデータ：

および からのデータ：

および からのデータ：

一変量関数の積である からのデータ：

一変量関数と二変量関数のおよび からのデータ：

三変量関数である,の密度スライスをプロットする：

指数関数の総和 sum_ialpha_i exp(-TemplateBox[{{p, -, {p, _, i}}}, Norm]^2)の等高面スライスをプロットする：

ボックスの中の点 をランダムに選び，そこから等高面スライスをプロットする：

他の可視化の方法と比較する：

それらを一緒に示す：

シミュレーションデータ  (3)

三変数の確率密度関数のスライスをプロットする：

サンプルを取り，関数をプロットする：

分布のシミュレーションを行い点を生成する：

ヒストグラムを使ってシミュレーションデータを累積する：

メンガーのスポンジ配列を生成し，そこから等高線スライスをプロットする：

配列中の半径1の近傍の値を平均し密度スライスをプロットすることで，ランダムな値の二次元配列の離散発散モデルのシミュレーションを行う：

時間は 軸に沿って進化する．時点1，3，7のスナップショットを撮る：

経験的データ  (2)

タンパク質中の原子の位置をビンに入れ，そこから密度スライスをプロットする：

軸をピコメートル単位にして原子の集中を示す：

脳からのMRIデータを可視化する：

特性と関係  (5)

表面上の等高線にListSliceContourPlot3Dを使う：

データ値の完全な体積の可視化にListDensityPlot3Dを使う：

一定の値の表面にListContourPlot3Dを使う：

関数にSliceDensityPlot3Dを使う：

2Dの密度プロットにListDensityPlotを使う：

考えられる問題  (1)

一定の値のスライス面にはノイズが現れることがある：

関数 は選択されたスライス面上で一定である：

別のスライス面を選ぶと関数の理に叶った絵が与えられる：

Wolfram Research (2015), ListSliceDensityPlot3D, Wolfram言語関数， https://reference.wolfram.com/language/ref/ListSliceDensityPlot3D.html （2022年に更新）.

テキスト

Wolfram Research (2015), ListSliceDensityPlot3D, Wolfram言語関数， https://reference.wolfram.com/language/ref/ListSliceDensityPlot3D.html （2022年に更新）.

CMS

Wolfram Language. 2015. "ListSliceDensityPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/ListSliceDensityPlot3D.html.

APA

Wolfram Language. (2015). ListSliceDensityPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ListSliceDensityPlot3D.html

BibTeX

@misc{reference.wolfram_2024_listslicedensityplot3d, author="Wolfram Research", title="{ListSliceDensityPlot3D}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ListSliceDensityPlot3D.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_listslicedensityplot3d, organization={Wolfram Research}, title={ListSliceDensityPlot3D}, year={2022}, url={https://reference.wolfram.com/language/ref/ListSliceDensityPlot3D.html}, note=[Accessed: 14-November-2024 ]}