NegativeBinomialDistribution[n,p]
母数が n と p の負の二項分布を表す.


NegativeBinomialDistribution
NegativeBinomialDistribution[n,p]
母数が n と p の負の二項分布を表す.
詳細

- 負の二項分布における値
 の確率は,非負の整数については
の確率は,非負の整数については であり,その他の場合はゼロである. »
であり,その他の場合はゼロである. » - NegativeBinomialDistributionでは,n は任意の正の実数でよく,p は1以下の任意の非負の実数でよい.
- n が正の整数の場合,NegativeBinomialDistribution[n,p]は,成功確率が p の一連の試行において n 回成功するまでの失敗回数の分布を返す.
- 非整数母数 n についてのNegativeBinomialDistributionもまたポリヤ(Pólya)分布として知られている
- NegativeBinomialDistributionでは,n と p は無次元量でよい. »
- NegativeBinomialDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- NegativeBinomialDistribution[n,p]は,整数値
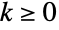 について定義され,正の実数母数 n および p (ただし,
について定義され,正の実数母数 n および p (ただし,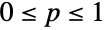 )によって定義された離散統計分布を表す.負の二項分布は離散的で単峰性の確率密度関数(PDF)を持つ.文脈によって,パスカル分布(PascalDistribution)およびPólya–Aeppli分布(PolyaAeppliDistribution)が負の二項分布と呼ばれることがあるが,どちらも上で説明した負の二項分布とは異なる.
)によって定義された離散統計分布を表す.負の二項分布は離散的で単峰性の確率密度関数(PDF)を持つ.文脈によって,パスカル分布(PascalDistribution)およびPólya–Aeppli分布(PolyaAeppliDistribution)が負の二項分布と呼ばれることがあるが,どちらも上で説明した負の二項分布とは異なる. - n が正の整数の場合,NegativeBinomialDistribution[n,p]は成功確率 p で n 回成功するまでの一連の試行における失敗数の分布を与える.これは,パスカル分布(PascalDistribution)に密接に関連しており,17世紀におけるパスカルの業績にまで遡ることができる.非整数母数 n について,負の二項分布はPólya分布としても知られている.一般的な n については,1940年代までにいくつかの分布が提唱され,負の二項分布と呼ばれていた.しかし,上で説明した(ずっと後になって提唱された)NegativeBinomialDistributionが,現代では最も広く応用されている.負の二項分布は1990年代以来確率論で非常に重要な役目を果たしており,事故統計,出生・死亡過程,消費支出,計量生物学,小売在庫管理等を含む現象のモデル化にも使われている.
- RandomVariateを使って,負の二項分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,NegativeBinomialDistribution[n,p]] (より簡略な表記では xNegativeBinomialDistribution[n,p])を使って,確率変数 x が負の二項分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[NegativeBinomialDistribution[n,p]]およびCDF[NegativeBinomialDistribution[n,p]]を使って得られる.平均,中央値,分散,共分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Covariance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が負の二項分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから負のパラメトリック二項分布を推定することが,FindDistributionParametersを使ってデータを負の二項分布にフィットすることができる.ProbabilityPlotを使って負の記号二項分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って負の記号二項分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された負の二項分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って負の二項分布を含む高次元分布を構築することが,ProductDistributionを使って負の二項分布を含む独立成分分布の結合分布を計算することができる.
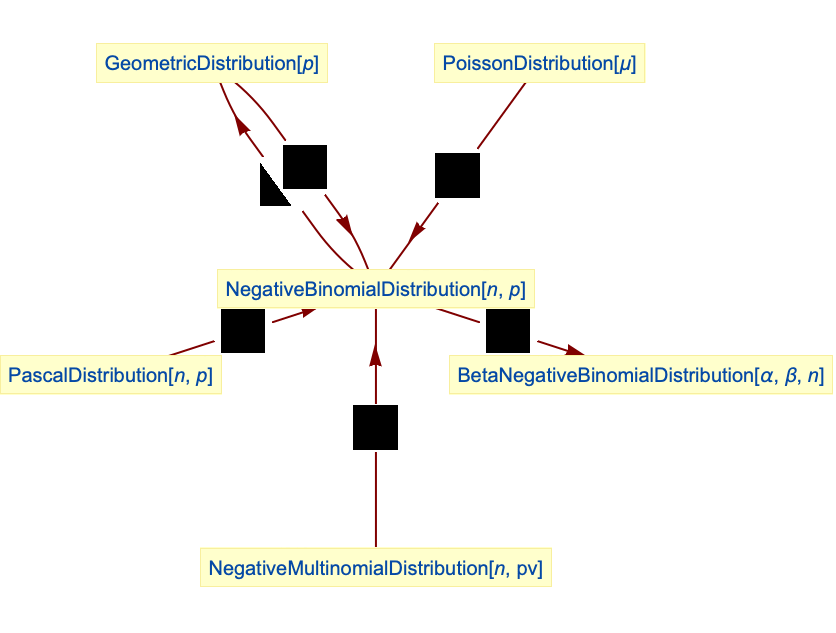
- NegativeBinomialDistributionは,他の数多くの分布と関連している.この分布は,NegativeBinomialDistribution[n,p]の変数 x についての確率密度関数が,ベクトル{x}について書かれたNegativeMultinomialDistribution[n,{1-p}]のそれと厳密に等しいという意味で,より一般的なNegativeMultinomialDistributionの一変量バージョンである.NegativeBinomialDistribution[1,p]はGeometricDistribution[p]とあらゆる面で等しい.NegativeBinomialDistributionはPascalDistributionとGeometricDistributionの変換分布(TransformedDistribution)として得ることができる.NegativeBinomialDistributionは,母数混合分布(ParameterMixtureDistribution)を使ってPoissonDistribution,GammaDistribution,BetaDistribution,BetaPrimeDistributionから実現することができる.また,より複雑な変換を介してCompoundPoissonDistributionとも関連している.NegativeBinomialDistributionはBinomialDistribution,MultinomialDistribution,BernoulliDistribution,BetaBinomialDistribution,HypergeometricDistribution,PoissonDistributionとも関連がある.
例題
すべて開く すべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
n が大きい場合,尖度は標準のNormalDistributionの尖度に近付く:
無次元のQuantityを使ってNegativeBinomialDistributionを定義する:
アプリケーション (7)
NegativeBinomialDistributionの累積分布関数は右連続関数の例である:
10回コイントスを行って,10回目のトスで8回目の表が出た.コインが公正な場合にこのような事象が起こる確率を求める:
コインが不正であるかもしれないと仮定して ![]() の最も考えられる値を求める:
の最も考えられる値を求める:
4回成功するまでフリースローを打つバスケットボールの選手がいる.この選手がフリースローで得点する確率は0.7である.プロセスのシミュレーションを行う:
1分間にファウルが行われる確率が独立して0.1であるとして30分間のファウルのシミュレーションを行う:
バスケットボールでは6回ファウルをすると退場になる.ファウルで退場になるまでの予想される競技時間を求める:
出荷される製品が60個一束で検査される.10個目の不良品が見付かると不合格となるが,すべての束がそれまで検査される.製品の20%が不良品である場合に束が不合格となる確率を求める:
不合格となった束にある不良品ではない製品の数のシミュレーションを行う:
不合格となった束に含まれる不良品に対する不良ではない製品の割合の平均を求める:
![]() 個のデータパケットを含むデータストリームが順序情報なしで繰り返し送られている.すべてのパケットが正しい順序で2回目に届くまでに届く順序が不正なデータストリームの数の分布を求める:
個のデータパケットを含むデータストリームが順序情報なしで繰り返し送られている.すべてのパケットが正しい順序で2回目に届くまでに届く順序が不正なデータストリームの数の分布を求める:
最高で18回失敗した後に,正しい順序のパケットが2回目に届く確率を求める:
特性と関係 (11)
NegativeBinomialDistribution[n,p]は n->∞で正規分布に収束する:
平均が固定している負の二項分布の極限はPoissonDistributionである:
負の二項分布を簡約するとGeometricDistributionになる:
負の二項分布とPascalDistributionはシフトによって異なる:
GeometricDistributionに従う n 個の独立変数の総和は負の二項分布に従う:
一変量のNegativeMultinomialDistribution は負の二項分布である:
NegativeBinomialDistributionはPoissonDistributionとGammaDistributionを混合したものである:
BetaNegativeBinomialDistributionは負の二項分布とBetaDistributionを混合したものである:
ゼロ切断NegativeBinomialDistributionの極限はLogSeriesDistributionである:
考えられる問題 (2)
テクニカルノート
-
▪
- 離散分布
関連するガイド
-
▪
- 離散一変量分布 ▪
- 壷モデル分布 ▪
- 保険数理で使われる分布
テキスト
Wolfram Research (2007), NegativeBinomialDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "NegativeBinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html.
APA
Wolfram Language. (2007). NegativeBinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html
BibTeX
@misc{reference.wolfram_2025_negativebinomialdistribution, author="Wolfram Research", title="{NegativeBinomialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html}", note=[Accessed: 09-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_negativebinomialdistribution, organization={Wolfram Research}, title={NegativeBinomialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html}, note=[Accessed: 09-February-2026]}