GammaDistribution

GammaDistribution[α,β]

形状母数 α，尺度母数 β のガンマ分布を表す．

GammaDistribution[α,β,γ,μ]

形状母数 α と γ，尺度母数 β，位置母数 μ の一般化されたガンマ分布を表す．

詳細

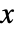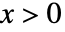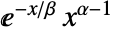  • ガンマ分布における値 の確率密度は，のときは に比例し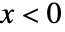，のときは0である． »
  • 一般化されたガンマ分布における値 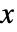の確率密度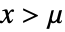は， では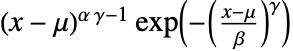に比例し，その他の場合は0である．
  • GammaDistributionでは，α，β，γ は任意の正の実数でよく，μ は任意の実数でよい．
  • GammaDistributionでは，β と μ は単位次元が等しい任意の数量でよく，α と γ は無次元量でよい． »
  • GammaDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »

予備知識

  • GammaDistribution[α,β,γ,μ]は，区間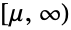上で定義され，実数 μ （「位置母数」と呼ばれる），2つの正の実数 α と γ（「形状母数」と呼ばれる），正の実数 β （「尺度母数」と呼ばれる）でパラメータ化された連続統計分布を表す．母数 μ は，ガンマ分布の確率密度関数(PDF)の水平位置を決定する．PDFの形は，α，β，γ の取る値の組合せに完全に依存し，単峰性か潜在的な特異値が領域の下方境界に近付く単調減少のいずれかである．これに加え，PDFの裾部は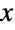， の大きい値についてPDFが指数的に減少するという意味で「薄い」（この動作は，分布のSurvivalFunctionを分析することで数量的に正確にできる）．4母数バージョンは一般化されたガンマ分布と呼ばれることがあるのに対し，2母数形式のGammaDistribution[α,β]（GammaDistribution[α,β,1,0]に等しい）は，しばしば単にガンマ分布と呼ばれる．
  • （2母数の）ガンマ分布は1830年代のラプラスの業績まで遡ることができる．ラプラスは，標準変量の精度についての後方共役事前分布としてこれを得た．3母数形式および4母数形式への一般化は，ディリクレ積分公式についてのリウヴィルの業績まで遡ることができる．ガンマ分布の名称は，そのPDFにガンマ関数が存在することによる．ガンマ分布は，さまざまな分野における数量をモデル化するために使われる．統計学では，ガンマ分布は，多変量正規分布に従う変量中の独立単位正規変量の平方和と関連する分布であり，正定値二次元形式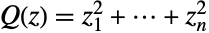（の形を持つもの）の分布の近似に使われる．ガンマ分布は，気象学，金融工学，統計生態学，個体群動態，ゲノミクス，神経科学，保険数理を含む他の多くの分野でも使われている．
  • RandomVariateを使ってガンマ分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,GammaDistribution[α,β,γ,μ]]（より簡略すると xGammaDistribution[α,β,γ,μ]）を使って，確率変数 x が，ガンマ分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[GammaDistribution[α,β,γ,μ],x]およびCDF[GammaDistribution[α,β,γ,μ],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がガンマ分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックガンマ分布を推定することが，FindDistributionParametersを使ってデータをガンマ分布にフィットすることができる．ProbabilityPlotを使って記号ガンマ分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号ガンマ分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたガンマ分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってガンマ分布を含む高次元分布を構築することが，ProductDistributionを使ってガンマ分布を含む独立成分分布の結合分布を計算することができる．
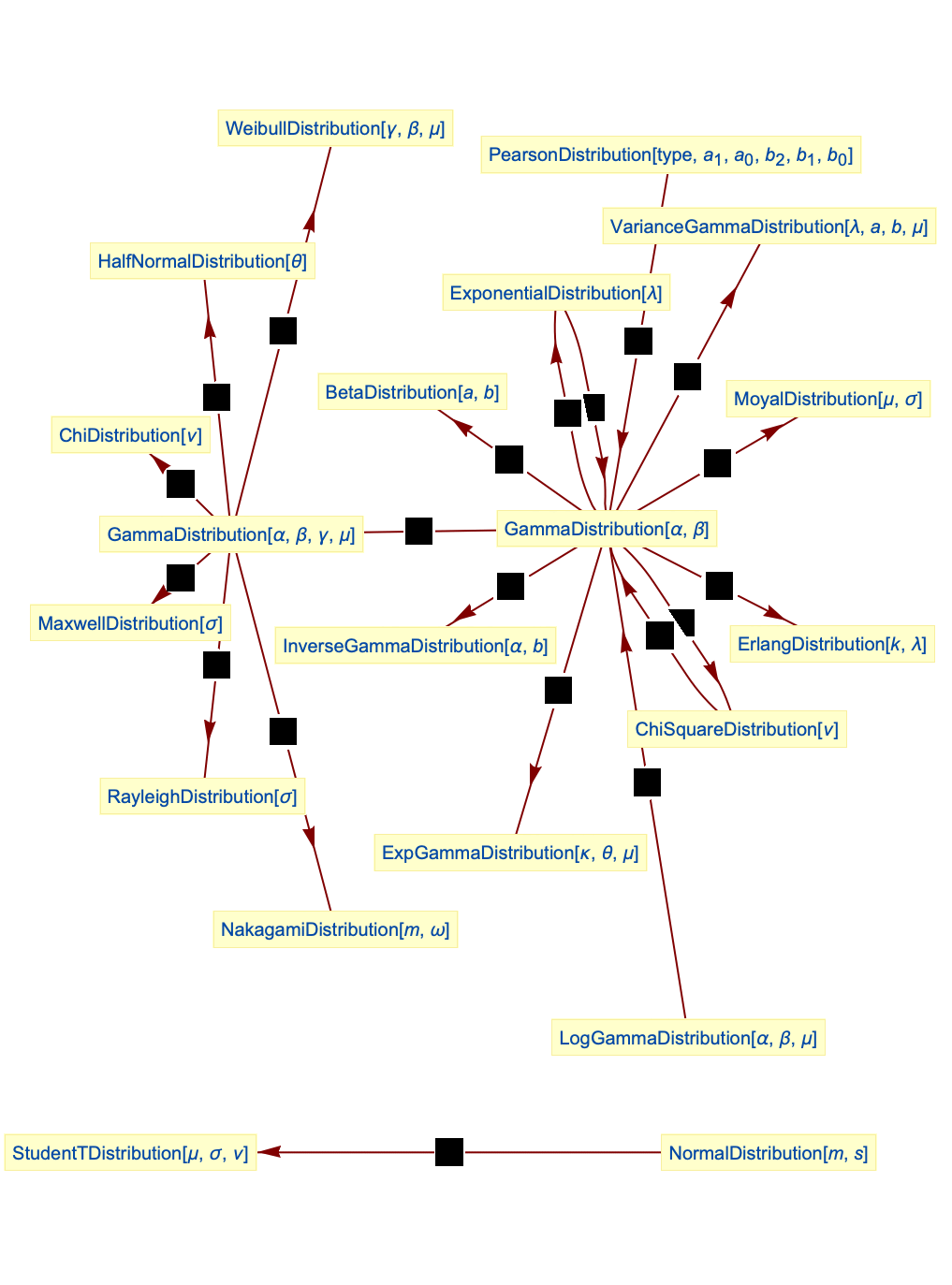
  • ガンマ分布は他のいくつかの分布と関連している．先述した通り，GammaDistributionはNormalDistributionおよびMultinormalDistributionと緊密な関係があり，PoissonDistribution，NormalDistribution，ExponentialDistribution，GompertzMakehamDistributionを含む（ベイズ推論では）いくつかの分布の共役事前分布である．GammaDistributionはChiSquareDistribution（GammaDistribution[ν/2,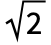,2,0]のPDFはChiSquareDistribution[ν]のPDFと同じである），ExponentialDistribution（ExponentialDistribution[1/λ]のPDFはGammaDistribution[1,λ]のPDFと同じである），MaxwellDistribution（MaxwellDistribution[σ]のPDFはGammaDistribution[3/2,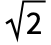σ,2,0]のPDFと厳密に等しい）に一般化される．これを変換してInverseGammaDistribution，MoyalDistribution，LogGammaDistribution等の分布を得ることができる．GammaDistributionは，PearsonDistribution，ErlangDistribution，BetaDistribution，ExpGammaDistribution，RayleighDistribution，ChiDistribution，WeibullDistribution，StudentTDistribution等とも関連している．

例題

すべて開くすべて閉じる

例  (8)

ガンマ分布の確率密度関数：

ガンマ分布の累積分布関数：

ガンマ分布の平均と分散：

ガンマ分布の中央値：

一般化されたガンマ分布の確率密度関数：

一般化されたガンマ分布の累積分布関数：

一般化されたガンマ分布の平均と分散：

一般化されたガンマ分布の中央値：

スコープ  (12)

ガンマ分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

一般化されたガンマ分布を示す擬似乱数の集合を生成する：

そのヒストグラムと確率密度関数を比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：


歪度は形状母数の α と γ のみに依存する：

ガンマ分布の歪度：

極限ではガンマ分布は対称になる：

一般化されたガンマ分布の歪度：

尖度は形状母数 α と γ のみに依存する：

ガンマ分布の尖度：

極限では尖度はNormalDistributionのものに近付く：

一般化されたガンマ分布の尖度：

母数の関数としての閉形式の種々のモーメント：

Moment：

記号次数の閉形式：

CentralMoment：

記号次数の閉形式：

FactorialMoment：

Cumulant：

記号次数の閉形式：

一般化されたガンマ分布の種々のモーメント：

Moment：

CentralMoment：

FactorialMoment：

Cumulant：

ガンマ分布のハザード関数：

の範囲での一般化されたガンマ分布のハザード関数：

の範囲：

ガンマ分布の分位関数：

一般化されたガンマ分布の分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

時間の中央値を求める：

アプリケーション  (6)

寿命がガンマ分布に従うデバイスがある．このデバイスの信頼性を求める：

で時間的に増大するハザード関数：

直列のこのようなデバイス2つの信頼性を求める：

並列のこのようなデバイス2つの信頼性を求める：

と について2つの系の信頼性を比較する：

寿命にA，B，Cの3段階があるデバイスがある．各段階の時間は平均が10時間の指数分布に従う．段階Cの後でこのデバイスは故障する．このデバイスの故障までの時間の分布を求める：

故障までの平均時間を求める：

このようなデバイスが最低40時間使用可能である確率を求める：

30個の独立したデバイスの故障までの時間のシミュレーションを行う：

朝の混雑する時間帯にある喫茶店に10分間に8人の客が来店する．1人の客が来店してから次の客が来店するまでの時間は指数分布に従い， 人の来店時間の間隔はGammaDistribution[k,1/λ]分布に従う．45分間に少なくとも40人が来店する確率を求める：

40番目の客が来店するまでの平均時間を求める：

40番目の客が来店するまでの時間が少なくとも1時間である確率を求める：

朝の混雑する時間帯に40番目の客が来店するまでの時間の30日間のシミュレーションを行う：

ガンマ分布の混合分布を使ってマルチモーダルデータのモデル化を行うことができる：

オールド・フェイスフル・ガイザーの噴出までの待ち時間のヒストグラムは2つのモードを示している：

MixtureDistributionをデータにフィットさせる：

そのヒストグラムを推定分布の確率密度関数と比較する：

待ち時間が80分を超える確率を求める：

平均待ち時間を求める：

最も一般的な待ち時間を求める：

次の60回の噴出の待ち時間のシミュレーションを行う：

ガンマ分布を使ってLogNormalDistributionに従うデータをモデル化することができる：

ヒストグラムと推定分布の確率密度関数を比較する：

対数尤度を対数正規分布による推定値と比較する：

Stacy分布は一般化されたGammaDistributionの特殊ケースである：

特性と関係  (32)

ガンマ分布は正の因子によるスケーリングの下では閉じている：

一般化されたガンマ分布は平行移動と正の因子によるスケーリングの下では閉じている：

ガンマ分布は加算の下では閉じている：

個の同一分布に従う変数について：

GammaDistribution[α,β]は α->∞ の極限で正規分布に収束する：

他の分布との関係：

ChiSquareDistributionはガンマ分布の特殊なケースである：

スケールされたChiSquareDistributionはガンマ分布に従う：

ChiDistributionはGammaDistributionの特殊ケースである：

ExponentialDistributionはガンマ分布の特殊なケースである：

ExponentialDistributionに従う 個の変量の総和はガンマ分布に従う：

の場合：

ガンマ分布とInverseGammaDistributionは逆分布の関係にある：

一般化されたガンマ分布はガンマ分布に簡約される：

MaxwellDistributionはGammaDistributionの特殊ケースである：

MoyalDistributionはGammaDistributionを変換したものである：

RayleighDistributionはGammaDistributionの特殊ケースである：

NakagamiDistributionはGammaDistributionの特殊ケースである：

WeibullDistributionは一般化されたガンマ分布の特殊ケースである：

HalfNormalDistributionは一般化されたガンマ分布の特殊ケースである：

一般化されたガンマ分布はガンマ分布からの変形として得ることができる：

ErlangDistributionはガンマ分布の特殊なケースである：

ガンマ分布はLogGammaDistributionに関連している：

GammaDistributionはExpGammaDistributionに関連している：

BetaPrimeDistributionは一般化されたGammaDistributionの商として得ることができる：

ParetoDistributionはGammaDistributionの商として得ることができる：

GammaDistributionはタイプ3のピアソン分布(PearsonDistribution)の特殊ケースである：

BetaDistributionは2つの独立したガンマ変数を変換したものとして得ることができる：

KDistributionはExponentialDistributionとGammaDistributionから得ることができる：

ガンマ分布の差はVarianceGammaDistributionに従う：

KDistributionはRayleighDistributionとGammaDistributionの母数混合として表すことができる：

NegativeBinomialDistributionはPoissonDistributionとGammaDistributionを混合したものである：

GeometricDistributionはPoissonDistributionとGammaDistributionを混合したものである：

StudentTDistributionはNormalDistributionとGammaDistributionの母数混合分布である：

ParetoDistributionはExponentialDistributionとGammaDistributionの商として求めることができる：

考えられる問題  (2)

GammaDistributionは，α あるいは β が正の実数ではないときは定義されない：

記号出力に無効な母数値を代入すると意味のない結果が返される：

おもしろい例題  (1)

累積分布関数の等高線を持つ β のさまざまな値についての確率密度関数：

Wolfram Research (2007), GammaDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/GammaDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), GammaDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/GammaDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "GammaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GammaDistribution.html.

APA

Wolfram Language. (2007). GammaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GammaDistribution.html

BibTeX

@misc{reference.wolfram_2024_gammadistribution, author="Wolfram Research", title="{GammaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GammaDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gammadistribution, organization={Wolfram Research}, title={GammaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/GammaDistribution.html}, note=[Accessed: 21-November-2024 ]}