SliceVectorPlot3D
SliceVectorPlot3D[{vx,vy,vz},surf,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
スライス面 surf 上に,場{vx,vy,vz}のベクトルプロットを生成する.
SliceVectorPlot3D[{vx,vy,vz},surf,{x,y,z}∈reg]
曲面 surf を領域 reg 内に制限する.
SliceVectorPlot3D[{vx,vy,vz},{surf1,surf2,…},…]
複数のスライス surfi上にベクトルプロットを生成する.
詳細とオプション




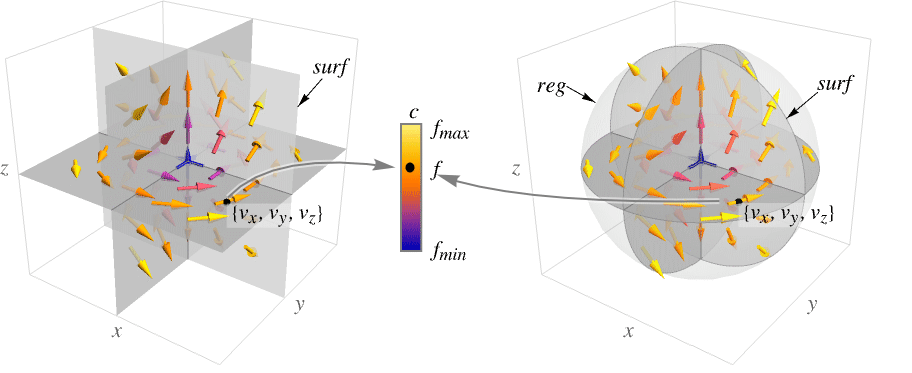
- SliceVectorPlot3Dは曲面 surf 上の x, y, z の値でフィールド関数{vx,vy,vz}を評価し,結果を大きさで彩色された矢印として表示する.
- このプロットは集合
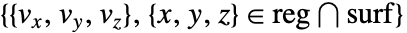 を可視化する.
を可視化する. - SliceVectorPlot3D[f,{x,xmin,xmax},…]はSliceVectorPlot3D[f,Automatic,{x,xmin,xmax},…]等に等しい.
- 以下の基本的なスライス面 surfiを与えることができる.
-
Automatic スライス面を自動的に決定する 
"CenterPlanes" 中心を通る座標平面 
"BackPlanes" プロットの後ろの座標平面 
"XStackedPlanes" 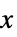 軸に沿って積み重ねられた座標平面
軸に沿って積み重ねられた座標平面
"YStackedPlanes" 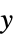 軸に沿って積み重ねられた座標平面
軸に沿って積み重ねられた座標平面
"ZStackedPlanes" 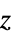 軸に沿って積み重ねられた座標平面
軸に沿って積み重ねられた座標平面
"DiagonalStackedPlanes" 対角上に軸に沿って積み重ねられた座標平面 
"CenterSphere" 中心の球 
"CenterCutSphere" 切り取られたウェッジがある球 
"CenterCutBox" 切り取られた象限があるボックス - 基本的なスライス面には次のパラメータ化を使うことができる.
-
{"XStackedPlanes",n}, n 個の等間隔の平面を生成する {"XStackedPlanes",{x1,x2,…}} x=xiについての平面を生成する {"CenterCutSphere",ϕopen} 視点に面したカット角 ϕopen {"CenterCutSphere",ϕopen,ϕcenter} 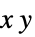 平面上の中心角が ϕcenterのカット角 ϕopen
平面上の中心角が ϕcenterのカット角 ϕopen - "YStackedPlanes"および "ZStackedPlanes"は"XStackedPlanes"についての指定に従う.追加的な特徴はスコープの例で示す.
- 次の一般的なスライス面 surfiを使うことができる.
-
expr0 x,y,z による陰的方程式,例:x y z-10 surfaceregion 3Dにおける二次元領域,例:Hyperplane volumeregion surfiが境界面とみなされる3Dにおける三次元領域,例:Cuboid - スライス面 surfiには次のラッパーを使うことができる.
-
Annotation[surf,label] 注釈を与える Style[surf,style] 曲面にスタイル付けする Button[surf,action] 曲面がクリックされた際に実行する動作を定義する EventHandler[surf,…] 曲面の一般的なイベントハンドラを定義する Hyperlink[surf,uri] 曲面がハイパーリンクとして動作するようにする PopupWindow[surf,cont] 曲面にポップアップウィンドウを付ける StatusArea[surf,label] 曲面上にマウスが来た場合にステータスエリアに表示する Tooltip[surf,label] 曲面に任意のツールチップを付ける - SliceVectorPlot3Dには,Graphics3Dと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
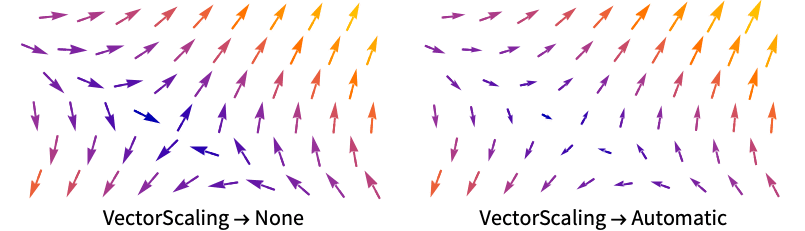
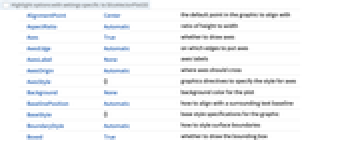
Axes True 軸を描くかどうか BoundaryStyle Automatic 表面の境界にどのようにスタイル付けするか BoxRatios {1,1,1} 縦横比 ClippingStyle Automatic ベクトル範囲外の矢印の表示方法 Method Automatic プロットに使うメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotLegends None 含める凡例 PlotPoints Automatic 各方向のスライス面 surfiについての近似サンプル数 PlotRange {Full,Full,Full} 含める x, y, z 値の範囲 PlotRangePadding Automatic 値の範囲をどのくらい充填するか PlotStyle Automatic 各スライス面についてのスタイル指示子 PlotTheme $PlotTheme プロットの全体的なテーマ RegionBoundaryStyle None プロット領域の境界のスタイル RegionFunction (True&) どの領域を含めるかを決定する ScalingFunctions None 軸のスケール方法 TargetUnits Automatic 希望する使用単位 VectorAspectRatio Automatic 矢印の縦横比 VectorColorFunction Automatic ベクトルをどのように彩色するか VectorColorFunctionScaling True VectorColorFunction引数をスケールするかどうか VectorMarkers Automatic 矢印の形 VectorPoints Automatic プロットするベクトルの数あるいは配置 VectorRange Automatic 表示するベクトル長の範囲 VectorScaling None 矢印のサイズのスケール方法 VectorSizes Automatic 表示された矢印のサイズ VectorStyle Automatic どのようにベクトルを描画するか WorkingPrecision MachinePrecision 内部計算に使う精度 - VectorScalingは,VectorSizesで与えられる sminから smaxの矢印のサイズの範囲にベクトルの大きさをスケールする.
- VectorScaling->Automaticは,ベクトルの大きさによって矢印の長さをスケールする.
- RegionFunctionには,x,y,z,vx,vy,vz,Norm[{vx,vy,vz}]が渡される.
- VectorColorFunctionには,デフォルトで,スケールされた x,y,z,vx,vy,vz,Norm[{vx,vy,vz}]が渡される.
- スライス面は,StyleラッパーおよびPlotStyleオプションでスタイル付けすることができる.Styleラッパーの方がPlotStyleより優先される.Noneを使ってスライス面を表示しないようにすることができる.
- 次は,ScalingFunctionsの可能な設定である.
-
{sx,sy,sz} x,y,z の各軸をスケールする - 次は,よく使われる組込みのスケーリング関数 s である.
-
"Log" 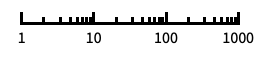
自動目盛ラベル付きの対数スケール "Log10" 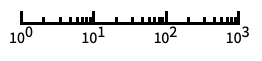
10のベキ乗に目盛が付いた,10を底とする対数スケール "SignedLog" 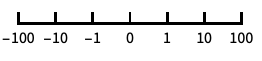
0と負の数を含む対数に似たスケール "Reverse" 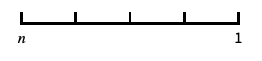
座標の向きを逆にする "Infinite" 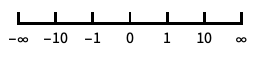
無限スケール
全オプションのリスト



例題
すべて開くすべて閉じるスコープ (28)
表面 (9)
立体プリミティブ上にプロットすることはRegionBoundary[reg]上にプロットすることに等しい:
サンプリング (3)
VectorPointsを使って矢印の数を指定する:
RegionFunctionを使って曖昧なスライスを露出させる:
領域はConeを含む領域で指定することができる:
ImplicitRegionを含む数式定義領域:
BoundaryMeshRegionを含むメッシュに基づく領域:
プレゼンテーション (16)
VectorScalingを使い,大きさに従ってスケールされた矢印を表示する:
VectorSizesを使って矢印が小さくなり過ぎないようにする:
VectorRangeを使ってどのベクトルをプロットするかを制御する:
ClippingStyleを使って切り取られたベクトルの外観を制御する:
PlotThemeを使って全体的なスタイルを即座に得る:
PlotLegendsを使ってさまざまな値に対する色の棒を得る:
Axesで軸の表示を制御する:
AxesLabelで軸に,PlotLabelでプロット全体にラベルを付ける:
VectorColorFunctionでベクトルをその大きさによって色付けする:
VectorMarkersを使ってベクトルの形を制御する:
VectorAspectRatioを使って矢印の縦横比を変更する:
BoundaryStyleでスライス面の境界にスタイル付けする:
RegionBoundaryStyleでRegionFunctionをハイライトする:
RegionBoundaryStyleでRegionFunctionにスタイル付けする:
TargetUnitsは,可視化でどの単位を使うかを指定する:
オプション (60)
BoxRatios (3)
ClippingStyle (4)
デフォルトで,切り取られたベクトルはVectorRangeが与える最短あるいは最長のベクトル長と一致する一定の色で彩色される:
PlotLegends (3)
場が2つのときにVectorColorFunctionをNoneに設定し,凡例を使ってそれぞれの場を識別する:
PlotRange (2)
PlotRangePadding (7)
PlotTheme (3)
RegionBoundaryStyle (3)
VectorRangeとClippingStyleを組み合せても同じような効果を出すことができる:
ScalingFunctions (4)
VectorAspectRatio (1)
VectorAspectRatioは矢印の長さの縦横比を指定する:
VectorColorFunction (5)
ColorDataからの任意の名前付き色勾配を使う:
VectorColorFunctionScaling->Falseを使ってスケールされていない値を得る:
VectorColorFunctionScaling (3)
VectorColorFunctionScaling->Falseを使ってスケールされていない値を得る:
VectorMarkers (3)
VectorPoints (4)
VectorRange (3)
VectorScaling (3)
VectorSizes (2)
VectorStyle (1)
VectorColorFunctionはVectorStyleより優先順位が高い:
アプリケーション (23)
微分方程式 (9)
微分方程式の解はすべてが原点に収束するプロット中の矢印に従う:
前述の例を自動化し,![]() についての実数固有値の可能なすべての符号の組合せを分析する.ただし,
についての実数固有値の可能なすべての符号の組合せを分析する.ただし,![]() は固有値が
は固有値が![]() の対角行列である:
の対角行列である:
![]() の場合は,
の場合は,![]() および
および ![]() 軸に沿った安定性はあるが,
軸に沿った安定性はあるが,![]() 軸に沿っては不安定である:
軸に沿っては不安定である:
![]() の場合は,
の場合は,![]() 軸に沿った安定性はあるが,
軸に沿った安定性はあるが,![]() および
および ![]() 軸に沿っては不安定である:
軸に沿っては不安定である:
![]() と直交する平面は
と直交する平面は ![]() と
と ![]() を含むので,原点は
を含むので,原点は ![]() では吸引的であり
では吸引的であり ![]() では反発的である:
では反発的である:
![]() と直交する平面は
と直交する平面は ![]() と
と ![]() を含むので,場は直接
を含むので,場は直接 ![]() に向かっている:
に向かっている:
![]() と直交する平面は
と直交する平面は ![]() と
と ![]() を含んでいるので,場は
を含んでいるので,場は ![]() から離れていく:
から離れていく:
![]() の固有値と固有ベクトルは,
の固有値と固有ベクトルは,![]() 軸周囲に螺線動作を持つベクトル場
軸周囲に螺線動作を持つベクトル場 ![]() の原点における流出域を示す:
の原点における流出域を示す:
いくつかの初期条件について,微分方程式 ![]() の線形系の解を計算する:
の線形系の解を計算する:
固有空間 ![]() は法線が
は法線が![]() の原点を通る平面なので,
の原点を通る平面なので,![]() の解は
の解は![]() の周りで螺旋運動をしつつ原点に引き寄せられる:
の周りで螺旋運動をしつつ原点に引き寄せられる:
![]() が1つの実数と2つの複素数の共役固有値を持つブロック対角である場合の微分方程式
が1つの実数と2つの複素数の共役固有値を持つブロック対角である場合の微分方程式 ![]() の線形系の動作を説明する.行列
の線形系の動作を説明する.行列 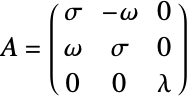 は,
は,![]() ,
,![]() ,
,![]() の固有値を持つ:
の固有値を持つ:
流体力学 (2)
固体力学 (2)
束 (3)
特性と関係 (10)
ベクトル場のすべての完全体積可視化にVectorPlot3Dを使う:
データにListSliceVectorPlot3Dを使う:
2Dにおけるベクトル点にVectorPlotを使う:
StreamPlotあるいはLineIntegralConvolutionPlotを2Dにおけるベクトル場に使う:
VectorDensityPlotを使ってスカラー場の密度プロットを加える:
StreamDensityPlotを使ってベクトルの代りに流れを使う:
VectorDisplacementPlotを使って変位ベクトル場の指定領域に対する影響を可視化する:
VectorDisplacementPlot3Dを使って変位ベクトル場の3Dの指定領域に対する影響を可視化する:
StreamPlot3Dを使って3D場を流線としてプロットする:
ComplexVectorPlotで複素関数をベクトル場としてプロットする:
ComplexStreamPlotでベクトルの代りに流れをプロットする:
GeoVectorPlotを使って地図上にベクトルをプロットする:
GeoStreamPlotでベクトルの代りに流れを使う:
テキスト
Wolfram Research (2015), SliceVectorPlot3D, Wolfram言語関数, https://reference.wolfram.com/language/ref/SliceVectorPlot3D.html (2022年に更新).
CMS
Wolfram Language. 2015. "SliceVectorPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/SliceVectorPlot3D.html.
APA
Wolfram Language. (2015). SliceVectorPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SliceVectorPlot3D.html