SliceVectorPlot3D
SliceVectorPlot3D[{vx,vy,vz},surf,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
在切片曲面 surf 上生成场 {vx,vy,vz} 的向量图.
SliceVectorPlot3D[{vx,vy,vz},surf,{x,y,z}∈reg]
将曲面 surf 限制在 reg 区域内.
SliceVectorPlot3D[{vx,vy,vz},{surf1,surf2,…},…]
在多个切片曲面 surfi 上生成向量图.
更多信息和选项




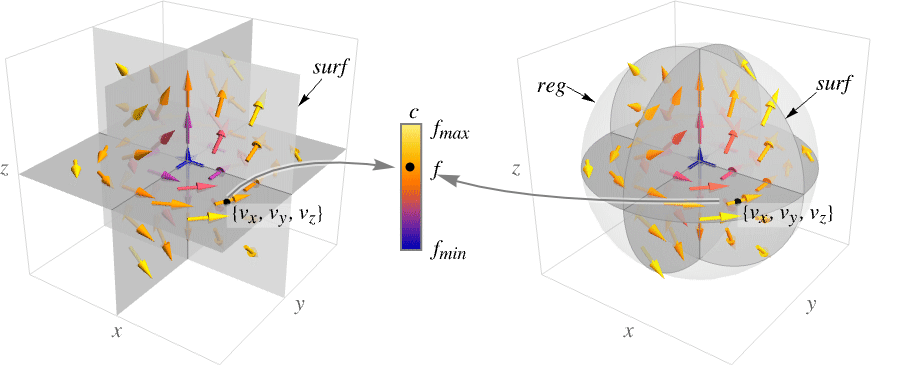
- SliceVectorPlot3D 在曲面 surf 上的 x、y 和 z 值处计算场函数 {vx,vy,vz} ,并将结果显示为按大小着色的箭头.
- 绘图可视化了集合
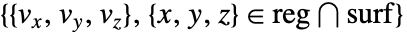 .
. - SliceVectorPlot3D[f,{x,xmin,xmax},…] 等价于 SliceVectorPlot3D[f,Automatic,{x,xmin,xmax},…] 等.
- 可以给出以下基本切片曲面 surfi:
-
Automatic 自动确定切片曲面 
"CenterPlanes" 经过中心的坐标平面 
"BackPlanes" 坐标平面位于图的后面 
"XStackedPlanes" 沿  轴堆叠的坐标平面
轴堆叠的坐标平面
"YStackedPlanes" 沿 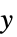 轴堆叠的坐标平面
轴堆叠的坐标平面
"ZStackedPlanes" 沿 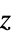 轴堆叠的坐标平面
轴堆叠的坐标平面
"DiagonalStackedPlanes" 沿对角方向堆叠的平面 
"CenterSphere" 位于中心的球面 
"CenterCutSphere" 切去楔形块的球面 
"CenterCutBox" 八分之一被切掉的盒子 - 以下参数化可用于基本切片曲面:
-
{"XStackedPlanes",n}, 生成 n 个等间隔平面 {"XStackedPlanes",{x1,x2,…}} 生成平面 x=xi {"CenterCutSphere",ϕopen} 正对视点处切去角 ϕopen {"CenterCutSphere",ϕopen,ϕcenter} 以  平面上的 ϕcenter 为中心角切去角 ϕopen
平面上的 ϕcenter 为中心角切去角 ϕopen - "YStackedPlanes"、"ZStackedPlanes" 和 "XStackedPlanes" 的规范一样,在“范围”下面的例子中会展示更多的用法.
- 可以使用下列常见切片表面 surfi:
-
expr0 以 x、y、z 表示的隐方程,如 x y z-10 surfaceregion 三维空间中的二维区域,如 Hyperplane volumeregion 三维空间中的三维区域,其中 surfi 为边界曲面,如 Cuboid - 可将下列封装用于切片曲面 surfi:
-
Annotation[surf,label] 提供注释 Style[surf,style] 为曲面设计样式 Button[surf,action] 定义当曲面被点击时应执行的操作 EventHandler[surf,…] 为曲面定义通用事件处理程序 (general event handler) Hyperlink[surf,uri] 将曲面设置为超链接 PopupWindow[surf,cont] 为曲面添加弹出窗口 StatusArea[surf,label] 当鼠标悬停在曲面处时,在状态栏中显示的内容 Tooltip[surf,label] 为曲面添加任意提示条 - SliceVectorPlot3D 与 Graphics3D 的选项相同,不同之处和更多选项如下所示: [所有选项的列表]
-
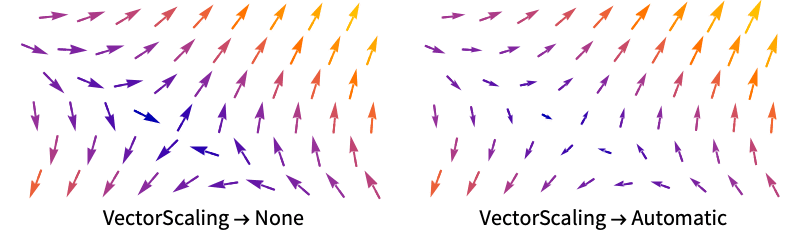
Axes True 是否绘制坐标轴 BoundaryStyle Automatic 如何设计曲面边界的样式 BoxRatios {1,1,1} 高宽比 ClippingStyle Automatic 怎样显示向量范围外的箭头 Method Automatic 用于绘图的方法 PerformanceGoal $PerformanceGoal 优化的目标 PlotLegends None 要包括的图例 PlotPoints Automatic 每个方向上切片曲面 surfi 样本的大致数目 PlotRange {Full,Full,Full} 要包括的 x、 y、 z 值范围 PlotRangePadding Automatic 取值范围填充为多少 PlotStyle Automatic 每个切片曲面的样式指令 PlotTheme $PlotTheme 图的整体主题 RegionBoundaryStyle None 怎样设置绘图区域边界的样式 RegionFunction (True&) 确定要包括哪块区域 ScalingFunctions None 怎样缩放坐标轴 TargetUnits Automatic 想要使用的单位 VectorAspectRatio Automatic 箭头的宽长比 VectorColorFunction Automatic 如何为向量上色 VectorColorFunctionScaling True 是否缩放传递给 VectorColorFunction 的参数 VectorMarkers Automatic 箭头的形状 VectorPoints Automatic 要绘制向量的数目或位置 VectorRange Automatic 显示出来的向量的长度范围 VectorScaling None 怎样缩放箭头的大小 VectorSizes Automatic 显示出来的箭头的尺寸 VectorStyle Automatic 如何绘制向量 WorkingPrecision MachinePrecision 内部计算时使用的精度 - VectorScaling 将向量的幅值缩放至由 VectorSizes 给定的箭头大小范围 smin 到 smax.
- VectorScaling->Automatic 将根据向量的幅值缩放箭头的长度:
- 传递给 RegionFunction 的变量为 x、y、z、vx、vy、vz 和 Norm[{vx,vy,vz}].
- 默认情况下,传递给 VectorColorFunction 的变量为经过缩放的 x、y、z、vx、vy、vz 和 Norm[{vx,vy,vz}].
- 可以用 Style 封装和 PlotStyle 选项来设计切片曲面的样式,其中 Style 封装比 PlotStyle 有更高的优先级. None 可以用来表示不应显示切片曲面.
- ScalingFunctions 的可能设置包括:
-
{sx,sy,sz} 缩放 x、y 和 z 坐标轴 - 常见内置缩放函数 s 包括:
-
"Log" 
对数刻度,自动进行标记 "Log10" 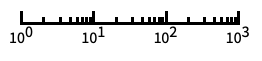
以 10 为底的对数刻度,用 10 的幂进行标记 "SignedLog" 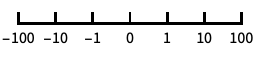
类似对数的刻度,包含 0 和负数 "Reverse" 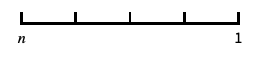
反转坐标的方向 "Infinite" 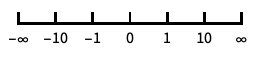
无穷刻度
所有选项的列表


范例
打开所有单元关闭所有单元范围 (28)
曲面 (9)
在基本几何体(volume primitive)上绘图相当于在 RegionBoundary[reg] 上绘图:
抽样 (3)
用 VectorPoints 指定箭头的数量:
用 RegionFunction 来显示被遮挡的切片:
可以用包含 Cone 的区域来指定值域:
一个含有 ImplicitRegion 的公式区域(formula region):
一个含有 BoundaryMeshRegion 的基于网格的区域:
演示 (16)
用 VectorScaling 显示根据幅值缩放的箭头:
用 VectorSizes 防止箭头太小:
用 VectorRange 控制绘制哪些向量:
用 ClippingStyle 控制剪切掉的向量的外观:
使用 PlotTheme 对整体样式进行配置:
使用 PlotLegends 显示不同数值对应的颜色:
用 Axes 控制坐标轴的显示:
可使用 AxesLabel 为坐标轴添加标签,使用 PlotLabel 为整个图添加标签:
可使用 VectorColorFunction 根据向量的幅值为向量添加颜色:
用 VectorMarkers 控制向量的形状:
用 VectorAspectRatio 修改箭头的宽长比:
用 BoundaryStyle 为切片曲面边界设计样式:
突出显示具有 RegionBoundaryStyle 的 RegionFunction:
用 RegionBoundaryStyle 设置 RegionFunction 的样式:
TargetUnits 指定了在可视化图中使用的单位:
选项 (60)
ClippingStyle (4)
默认情况下,剪切掉的向量具有恒定的颜色,该颜色与 VectorRange 给出的最小或最大的向量长度的颜色一致:
PlotLegends (3)
PlotRange (2)
PlotRangePadding (7)
PlotTheme (3)
RegionBoundaryStyle (3)
VectorAspectRatio (1)
VectorAspectRatio 指定箭头的宽长比:
VectorColorFunction (5)
可使用 ColorData 中任意有名称的颜色梯度:
使用 VectorColorFunctionScaling->False 可得到未经缩放的值:
VectorColorFunctionScaling (3)
VectorMarkers (3)
VectorRange (3)
VectorScaling (3)
VectorSizes (2)
VectorStyle (1)
VectorColorFunction 比 VectorStyle 的优先级高:
应用 (23)
属性和关系 (10)
用 VectorPlot3D 可视化整个矢量场:
对数据使用 ListSliceVectorPlot3D:
用 VectorPlot 绘制二维向量图:
用 StreamPlot 或 LineIntegralConvolutionPlot 绘制二维向量场:
使用 VectorDensityPlot 添加标量场的密度图:
使用 StreamDensityPlot 可在图中使用流而非向量:
使用 VectorDisplacementPlot 来可视化位移向量场对指定区域的影响:
用 VectorDisplacementPlot3D 可视化位移向量场对指定三维区域的影响:
使用 StreamPlot3D 将三维场绘制为流线:
用 ComplexVectorPlot 将复函数绘制为向量场:
可用 ComplexStreamPlot 绘制流而非向量:
可用 GeoVectorPlot 在地图上绘制向量:
可用 GeoStreamPlot 绘制流而非向量:
文本
Wolfram Research (2015),SliceVectorPlot3D,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SliceVectorPlot3D.html (更新于 2022 年).
CMS
Wolfram 语言. 2015. "SliceVectorPlot3D." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/SliceVectorPlot3D.html.
APA
Wolfram 语言. (2015). SliceVectorPlot3D. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SliceVectorPlot3D.html 年
