TreePlot
TreePlot[g]
产生图 g 的树图.
TreePlot[{e1,e2,…}]
产生边为 ej 的树图.
TreePlot[{…,w[ei],…}]
绘制特征由符号封装 w 定义的 ei.
TreePlot[{vi 1vj 1,…}]
使用规则 vi 1vj 1 指定图 g.
TreePlot[m]
产生由邻接矩阵 m 表示的树图.
TreePlot[…,vpos]
将根 v 放在图的位置 pos.
更多信息和选项


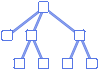
- TreePlot 也称为树形图.
- TreePlot 尝试把顶点放在连续层的树上或树的集合上.
- TreePlot 支持如 Graph 一样的顶点和边.
- 如果图 g 不是树,TreePlot 把其顶点布局在图的每个连接分量的生成树的基础上.
- TreePlot[g] 试图按照使树具有尽可能少的层次来选择根.
- TreePlot[g,pos] 把根放在位置 pos.
- 可能的位置 pos 是 Top、Bottom、Left、Right、Center.
- 默认情况下,TreePlot 把每个树根放在顶部.
- 以下特殊封装可以用在边 ei:
-
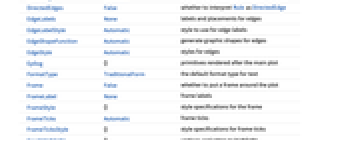
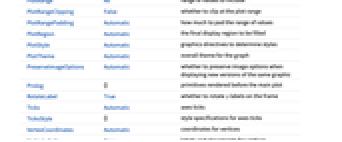
Annotation[ei,label] 提供注释 Button[ei,action] 定义当点击元素时执行的行为 EventHandler[ei,…] 定义元素的一般事件句柄 Hyperlink[ei,uri] 把元素作为超链接 Labeled[ei,…] 显示带有标签的元素 PopupWindow[ei,cont] 在元素上附加弹出窗口 StatusArea[ei,label] 当鼠标悬停在元素时显示在状态区 Style[ei,opts] 使用指定的样式显示元素 Tooltip[ei,label] 在元素上附加任意的提示条 - TreePlot 同 Graphics 具有相同的选项,添加及改变了下列选项: [所有选项的列表]
-
DataRange Automatic 生成顶点坐标的范围 DirectedEdges False 是否把 Rule 诠释为 DirectedEdge EdgeLabels None 边的标签和位置 EdgeLabelStyle Automatic 边标签使用的样式 EdgeShapeFunction Automatic 产生边的图形状 EdgeStyle Automatic 边的样式 GraphHighlight {} 突出显示的顶点和边 GraphHighlightStyle Automatic 突出显示的样式 LayerSizeFunction (1) 每一层允许的高度 PerformanceGoal Automatic 试图最优化的性能方面 PlotStyle Automatic 对顶点和边的整体图形指令 PlotTheme Automatic 图的整体主题 VertexCoordinates Automatic 顶点的坐标 VertexLabels None 顶点的标签和位置 VertexLabelStyle Automatic 用于顶点标签的样式 VertexShape Automatic 顶点的图形形状 VertexShapeFunction Automatic 产生顶点的图形形状 VertexSize Automatic 顶点的大小 VertexStyle Automatic 顶点的样式 - PlotTheme 的可能设置包括常用的基本主题:
-
"Business" 适于商业展示或信息图形的明亮、现代外观 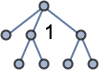
"Detailed" 通过使用标签和提示条识别数据 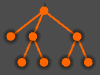
"Marketing" 适于市场需求的优雅、捉眼球的设计 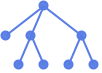
"Minimal" 简单图 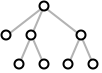
"Monochrome" 单颜色设计 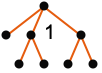
"Scientific" 坦率的设计对于分析带有标签和提示条的详细数据非常有用 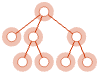
"Web" 干净、大胆的设计适于消费者的网站或博客 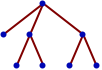
"Classic" 图的历史设计仍与现有用途保持兼容 - 图的特征主题影响顶点和边的绘制. 特征主题包括:
-
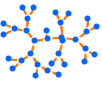
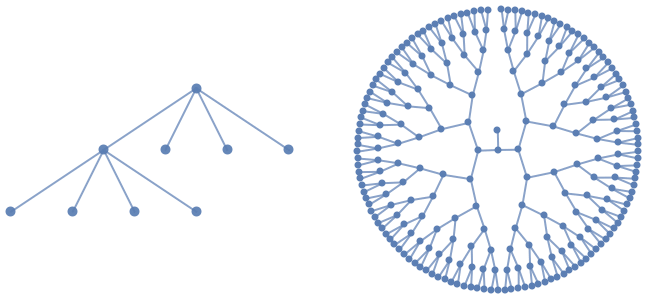
"LargeGraph" 大图 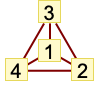
"ClassicLabeled" 典型的图 
"IndexLabeled" 索引标签图
所有选项的列表


范例
打开所有单元关闭所有单元范围 (10)
选项 (7)
PlotStyle (3)
PlotStyle 可以和有更高优先级 VertexRenderingFunction 混合使用:
PlotStyle 可以和有更高优先级的 EdgeRenderingFunction 混合使用:
应用 (8)
属性和关系 (4)
可能存在的问题 (2)
用 LayeredGraphPlot 或 GraphPlot 可以避免边的重叠:
TreePlot 自动选择根节点来最小化树的高度:
文本
Wolfram Research (2007),TreePlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TreePlot.html (更新于 2020 年).
CMS
Wolfram 语言. 2007. "TreePlot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/TreePlot.html.
APA
Wolfram 语言. (2007). TreePlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TreePlot.html 年