Wolfram言語では，どんな軸スケールを使うかとか，プロットする式のサンプリング点をどこにするかとか，また座標軸をどう描画するかとか，プロットの仕様をいろいろ変更できるようになっている．通常は，Wolfram言語により自動的に採用される設定条件で間に合うが，グラフの用途によっては，仕様を変更した方がよいときもあるだろう．

これはWolfram言語の関数全般に関して言えることだが，関数の動作条件を変更するには，「オプション」指定を行う．各オプションには決まった名前がある．例えば，プロットの条件を指定するにはPlot関数の最後に引数として，書式 name->value で書かれた規則を引数として加える（ここで，name はオプション名，value は変更する設定値を示す）．何も規則を指定しなければ，「デフォルト値」の規則が使われる．

Plotのような関数には設定できるオプションが数多くある．普通は，多くても2，3の項目を変更する程度で事が足りるだろう．プロットを見やすくするには，いろいろと実験してみるのが最善の方法である．例えば，あるオプションに一連の異なった値を設定していったとき，プロットの表示がどうなるかを見ていくとよいだろう．

オプションはプロットごとに指定することができる．また，プロットした後でも，オプションだけを変えて再表示することができるようにもなっている．これについては「プロットの再描画と組合せ」で説明する．

自動設定でプロットを行う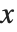と， 軸と 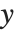軸のスケールが自動設定され，式の挙動で特に重要と思われる部分だけがプロットされる．もし，プロットする式の値が急激に増加する場合や，特異点が現れる場合は，局所的に式の値が大きくなりすぎて，その部分は自動的にプロット範囲から除外されてしまう．PlotRangeを指定することにより，プロットに入れたい 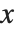軸と 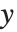軸の範囲を正確に制御できる．

関数の曲線をなるべく滑らかにプロットできるように，Wolfram言語内部で調整が取られる．つまり，増減の激しい関数に対してはより多くのプロット点が使われる．通常，関数の取る形に応じて関数のサンプリングを「適応」させるが，上限はあり，それ以上の細かさで関数をサンプリングすることはできない．この上限は設定可能なので，必要ならば変更しておく．

ここで重要なのは，プロットする関数は限られた点数までしかサンプリングできないので，必ずしも関数の特徴を再現できるとは限らない，ということである．Wolfram言語は適応的に関数をサンプリングするため，関心のある部分付近のサンプル数を増加させるが，それでも何かが足りないという可能性もある．もちろん，PlotPointsでプロット点数を増やしておき，もっと多くの点でサンプリングすることは可能である．ただし，PlotPointsを大きく設定すればするほど，曲線は滑らかにできるが，プロットする時間も長くなってしまうことになる．

一度プロットしたなら，いつでもそれを再表示できるようにプロット操作に関する情報がWolfram言語内部に保存される．このため，プロットを再表示するときは，必要なオプションだけを変更すればよい．

Showを入力するたびにオプション設定を変えてやることで，1つのプロットをいろいろな方法で見ることができる．最良なプロット仕様を見付けるには，このようにひとつひとつ設定条件を試しながら行うのもよい方法である．

Showを使い複数のプロットを重ねて表示することもできる．結果のグラフィックスのオプションはすべて，Show式の最初のグラフィックスのオプションを従う．

Wolfram言語のグラフィックスはすべて式なので，他の式と同様に操作することができる．このような操作を行うときはShowを使う必要はない．

書式Show[plot₁,plot₂,…]を使うと，複数のプロットを1つに重ね合せることができる．また，GraphicsGridを指定しておけば，複数のプロットを配列的に並べることもできる．

特に指定がない場合，GraphicsGridを指定するとプロットとプロットの境界に狭い間隔が置かれる．この間隔は，書式Spacings->{h,v}を使ったオプション設定で変えることができる．ここで，h と v は，それぞれ，水平方向と垂直方向の間隔幅を表すパラメータである．デフォルトでは，Spacingsオプションはデフォルトフォントの文字の幅と高さを使って，h および v パラメータをスケールするが，グラフィックスでは一般にScaled座標を使った方が便利である．Scaledは値1が格子の1要素の幅と高さを表すようにスケールする．

プロットすると，他の情報と一緒にプロットした点もリスト形式で保存される．Showを使うことで，これらの情報をもとに，プロットをいろいろな描画条件で再表示することができる．また，条件を変えても，Showにはもともとプロットした値が保存されているので，例えば，オプション設定で最初に作ったプロットを部分的に拡大表示させ，Plotで使われた個々の標本点を確認する，というようなことも可能である．ただし，オプションPlotPointsを使ったプロット点数の指定は，Plotコマンドを指定したときだけに有効である．（Wolfram言語では，常に保持してある実際の点がプロットされる．平滑化した曲線やスプライン曲線は使われない．これは，数学のグラフィックスで誤った解釈を与えかねないからである．）

三次元グラフィックスは，その内部でマウスをドラッグしてグラフィックスを回転させることができる．グラフィックスの内部でドラッグすると，グラフィックスはマウスに従う方向に転倒し，グラフィックスの境界線付近をドラッグするとスクリーン上のそのままの場所で回転する．Shiftキーを押したままグラフィックスをドラッグすると，グラフィックスをパンすることができる．Ctrlキーを使うとズームされる．

3Dプロットには非常に多くのオプションがある．ここではその中の基本的なものに限って説明する．他は「グラフィックスとサウンドオブジェクトの構造」で説明する．

次に掲げる3Dプロットの最初のオプション群は，2D用に提供される同名のオプションと機能面で同じである．

3Dプロットで特に重要な設定はどこの空間点からプロット面を眺めるかを決めることだろう．実際の設定は，視点となる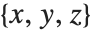の座標位置を選び，オプションViewPointに設定することで行える．Plot3DとShowの機能のどちらでも設定の仕方は同じである．座標の算出法は「3Dグラフィックスの座標系」で説明する．マウスを使ってグラフィックスを回転させている場合は，ViewPoint値を調整していることになる．

人間は，複雑な数学的曲面を視覚的にとらえるのがどちらかというと苦手である．曲面の形を把握しやすくするためには，理解を助けるような手掛りをできるだけ多くプロットに入れておくとよい．

視点に関しては，プロット面を多少斜め上方向から眺めるような値に設定するとたいていは最良の効果が得られる．また，視点をプロット面にある程度接近させ，遠近効果を付けた方が一般によくなる．また，プロット空間に囲み枠を引いて，プロット面の空間配置（オリエンテーション）を分かりやすくするのもひとつの方法だろう．

3Dのイメージに実在感を与えるために，デフォルトでは，擬似的な照明モデルを使いプロット面に特殊な色付けが施される．この場合，4点の光源とアンビエント照明がオブジェクトを照らしているものと想定される．他の光源の設定方法やオブジェクトの反射特性の設定方法は，「照明効果と曲面の反射特性」で説明する．

照明は，照明特性の集まりを表す文字列を使って指定することもできる．例えば，オプション設定Lighting->"Neutral"では白い光の集まりが使われるので，プリンタ等の白黒出力デバイスで忠実に再現することができる．

Wolfram言語を使って関数の値をプロットすることができる．Wolfram言語に関数を入力し，それを複数のプロット点で評価することで曲線や曲面を形成させる．

ここでは関数ではなく，リストとしてあるデータ点をどうプロットするかを説明する（外部ファイルやプログラムからどうデータを読み込むかは，「データのインポートとエキスポート」で説明する）．プロットの対象物がリスト形式のデータであっても，使うWolfram言語コマンドは，関数のプロットで使ったものと似ていて，類推できる．

「基本的なプロット」において，Wolfram言語を使いどう 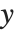座標を 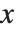座標の関数としてプロットし，曲線を生成するかを説明した．Wolfram言語を使いパラメトリックプロットを行うことも可能である．パラメトリックプロットでは，各点の 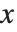と 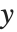座標は，ともに第3のパラメータ，例えば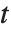， に依存した関数として与えられる．

3Dパラメトリックプロットで使うParametricPlot3D[{f_x,f_y,f_z},{t,t_min,t_max}]は，二次元のParametricPlot[{f_x,f_y},{t,t_min,t_max}]に準じている．また，どちらの次元のプロットでも，パラメータ t を変化させることでプロット点が生成され，また，それらの点が結ばれることで曲線が形成される．ParametricPlotなら曲線は二次元，ParametricPlot3Dなら三次元である．

ParametricPlot3D[{f_x,f_y,f_z},{t,t_min,t_max},{u,u_min,u_max}]を使うと，形成されるのは3Dの曲面で，曲線ではない．曲面は四辺形の面要素で構成され，四辺形の各頂点は，等間隔の格子上で t と u が取る値において決定される f_i の各値に対応した座標を持つ．

ParametricPlot3Dをうまく使えば，複雑に入り組んだ構造の曲面を作ることができる．このような曲面の形成の仕方は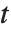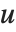，- 平面を「歪めたり」，「丸めたり」して行うものととらえると分かりやすいかもしれない．

ParametricPlot3Dで曲面プロットをするときは，特に，パラメータとして適切な変数を選択することが大切である．また，パラメータを変化させていったときプロット面が部分的にでも複数回に渡って描画されないように注意しなければいけない．同じ点を何回もプロットするとメッシュが部分的に途切れてしまうことがあるし，また，ParametricPlot3Dがプロットを完了するのに余計な時間がかかってしまう．

「グラフィックスとサウンドオブジェクトの構造」で触れるが，Wolfram言語には機能的に非常に充実したグラフィックス用プログラミング言語が組み込まれている．この言語を使うことで，いろいろな形式のプロットを行うことが可能になる．

利用できるプロット関数のいくつかが，Wolframシステムに付属の標準パッケージで定義されている．

Wolframシステムを使えばグラフィックスだけでなくサウンドも作れる（一部のコンピュータではシステム的に制約がありこの機能がサポートされない場合がある）．Wolframシステムでは，グラフィックスとサウンドはほとんど同じように扱われる．

例えば，グラフィックスでは，Plot[f,{x,x_min,x_max}]により関数をプロットする．これに対して，サウンドでは，Play[f,{t,0,t_max}]により関数を「プレイ」する．Playでは，関数が音の波形の定義に使われる．また，関数の値は，時間の関数である発生音の振幅を与える．

Playのサウンドはどんな波形の音でもよい．例えば，倍音で構成されたものでなくてもよい．Playの引数として入力する振幅関数は，発生させたい音に対応した瞬間信号値を与えるものである．この信号は，まず電圧に変換され，そして，スピーカの振動に変換されて音を発生させる．文献によっては，振幅は音のピーク信号強度と定義するものもあるが，本書では，常に，時間の関数である瞬間的な信号強度とする．

Playで使う時間変数は常に秒単位で指定する．実際に音の生成が開始されると，音の振幅が毎秒決まった回数だけ標本化（サンプリング）される．この毎秒当りのサンプル数はサンプルレートと呼ばれ，オプションSampleRateを使うことで任意な値に設定することができる．

一般に，サンプルレートを上げると，高い周波数帯域の音成分をより忠実に表現できるようになる．サンプルレートがr であれば再生可能な周波数域は 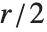Hzまでである．普通，人間の聴力は周波数で20〜22,000Hzの音を聞き取ることができるといわれている（年齢や性別等によって多少差はある）．ちなみに，ピアノの持つ88音階は基本周波数で27.5〜4,096Hzに相当する．

また，CDプレーヤーで使われている標準サンプルレートは44,100Hzで，実効的な電話のサンプルレートは8,000Hz程度である．特別なシステム仕様でなければ，Wolframシステムにおけるサンプルレートは，規定で約8,000Hzに設定されている．

Play[{f₁,f₂,…]を使いステレオ効果を出すこともできる．2チャンネルにとどまらず，何チャンネルでも操作可能である．

ListPlayを使いデータを音として聞くことが可能である．この場合，データはリスト形式で入力し，各データ点は特定のレートでサンプリングされた振幅の値とする．

Wolframシステムで実際にサウンドが生成される場合，一定範囲の振幅・音域だけが許される．これは，PlayまたはListPlayのコマンドにオプションPlayRangeを使った区間値を与えることでできる．この設定は，「プロット仕様の変更」のプロット範囲の指定で使ったPlotRangeと同じように行えばよい．

設定PlayRange->Automaticを使えば，適切なスケール率が選択され便利だが，PlayRangeを使い音域を限定した方が，内部でプレイ範囲の計算をする必要がなくなるため，Playの処理スピードが上がる．

出力のSoundオブジェクトは通常，サウンドの可視化を含むボタンとしてフォーマットされ，押されたときにサウンドを発する．サウンドはユーザが介入しなくても，またEmitSoundを使って出力を生成しなくてもプレイすることができる．事実，Soundボタンの内部の内装ではボタンが押されたときにEmitSoundが使われる．

Soundオブジェクトの内部構造は，「サウンド表現」で説明する．