SphericalPlot3D
SphericalPlot3D[r,θ,ϕ]
球座標 θ と ϕ の関数として,球面半径 r の3Dプロットを生成する.
SphericalPlot3D[r,{θ,θmin,θmax},{ϕ,ϕmin,ϕmax}]
球座標の指定した範囲で3D曲面プロットを生成する.
SphericalPlot3D[{r1,r2,…},{θ,θmin,θmax},{ϕ,ϕmin,ϕmax}]
複数の曲面を持つ3D曲面プロットを生成する.
詳細とオプション




- 角
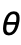 および
および 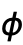 はラジアンで測られる.
はラジアンで測られる. 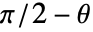 は「緯度」に相当する.
は「緯度」に相当する. は「北極」で0に,「南極」で
は「北極」で0に,「南極」で 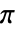 になる.
になる.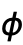 は「経度」に相当し,「北極」から見て0から
は「経度」に相当し,「北極」から見て0から  まで反時計回りで変化する.
まで反時計回りで変化する.- SphericalPlot3D[r,θ,ϕ] は
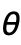 が0から
が0から 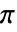 まで,
まで,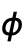 が0から
が0から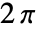 までの範囲であるとする.
までの範囲であるとする.  ,
, 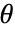 ,
, 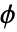 に相当する
に相当する 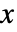 ,
, 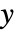 ,
, 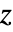 位置は,
位置は, ,
, 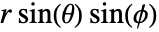 ,
, 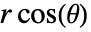 である.変数
である.変数 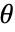 および変数
および変数  は任意の値を持つことができる.これらが定義する曲面は放射状に重なってもよい.
は任意の値を持つことができる.これらが定義する曲面は放射状に重なってもよい.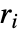 等を評価するとNone,あるいは実数以外になる位置には穴が残される.
等を評価するとNone,あるいは実数以外になる位置には穴が残される.- SphericalPlot3Dは,実質的にBlockを使って変数
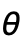 と
と 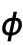 変数を局所的に扱う.
変数を局所的に扱う. - SphericalPlot3Dは属性HoldAllを持ち,変数に特定の数値を割り当てた後でのみ
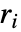 を評価する.
を評価する. - 場合によっては,変数に特定の数値を割り当てる前にEvaluateを使って
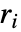 を記号的に評価する方が効率がよいことがある.
を記号的に評価する方が効率がよいことがある. - SphericalPlot3Dでは,Graphics3Dのオプションに以下の追加・訂正を加えたものが使える. [全オプションのリスト]
-
Axes True 軸を描くかどうか BoundaryStyle Automatic 曲面の境界線をどのように描くか ColorFunction Automatic 曲線と曲面の色をどのように決めるか ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか EvaluationMonitor None 各関数を評価するときに評価する式 Exclusions Automatic 除外すべき 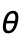 および
および 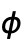 曲線
曲線ExclusionsStyle None 除外された点または曲線の部分に何を描くか MaxRecursion Automatic 許容する再帰分割の最大数 Mesh Automatic 各方向にいくつのメッシュ分割を描くか MeshFunctions {#4&,#5&} メッシュ分割の置き方をどう決めるか MeshShading None メッシュ分割間の陰影付けの方法 MeshStyle Automatic メッシュ分割のスタイル Method Automatic 曲面の細分化に使用するメソッド NormalsFunction Automatic 効果的な曲面の法線をどのように決定するか PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotLegends None 曲面の凡例 PlotPoints Automatic 各パラメータのサンプル点の最初の数 PlotStyle Automatic 各オブジェクトのスタイルに使うグラフィックス指示子 PlotTheme $PlotTheme プロットの全体的なテーマ RegionFunction (True&) 点を含めるかどうかの決定方法 ScalingFunctions None 個々の座標のスケール方法 TextureCoordinateFunction Automatic テクスチャ座標の決め方 TextureCoordinateScaling True TextureCoordinateFunctionの引数をスケールするかどうか WorkingPrecision MachinePrecision 内部計算の精度 - Tooltip,StatusArea,あるいはAnnotationを使って曲線や曲面にインタラクティブにラベルを付けることができる.
- SphericalPlot3D[Tooltip[{r1, r2,…}],…]は,
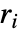 が対応する曲面のツールチップのラベルとして表示されるように指定する.
が対応する曲面のツールチップのラベルとして表示されるように指定する. - Tooltip[r,label]は,曲面の明示的なツールチップラベルを指定する.
- SphericalPlot3Dは,まず,PlotPointsが指定する多くの等間隔に置かれたサンプル点で各関数を評価する.次に,最大でMaxRecursion回各パラメータを再分割し,適応的アルゴリズムを使って追加的なサンプル点を選ぶ.
- 使うサンプル点の数が有限であれば,SphericalPlot3Dが関数の特徴を見逃す可能性があるので注意されたい.結果の検証にはPlotPointsとTMaxRecursionの設定値を大きくするとよい.
- On[SphericalPlot3D::accbend]のとき,曲線が一定の滑らかさに達しないときにSphericalPlot3Dはメッセージを出力する.
- MeshFunctionsおよびRegionFunctionで関数に渡される引数は
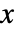 ,
,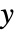 ,
,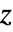 ,
,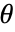 ,
,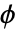 ,
,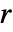 である.ColorFunctionとTextureCoordinateFunctionの関数には,デフォルトでこれらの引数のスケールされたものが渡される.
である.ColorFunctionとTextureCoordinateFunctionの関数には,デフォルトでこれらの引数のスケールされたものが渡される. - これらの関数は各曲面上に渡って評価される.
- デフォルトで,曲面はColorFunction->(White&)に相当する均一の白い拡散反射面として扱われる.
- SphericalPlot3DはGraphics3D[GraphicsComplex[data]]を返す.
- 3D曲面に影響するテーマ
-

"DarkMesh" 色の濃いメッシュライン 
"GrayMesh" グレーのメッシュライン 
"LightMesh" 色の薄いメッシュライン 
"ZMesh" 垂直に配置されたメッシュライン 
"ThickSurface" 曲面に厚みを与える - 次は,ScalingFunctionsの可能な設定である.
-
{sx,sy,sz} x,y,z の各軸をスケールする {sx,sy,sz,sθ,sϕ} θ パラメータ空間と ϕ パラメータ空間をスケールする - 次は,よく使われる組込みのスケーリング関数 s である.
-
"Log" 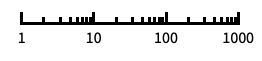
自動目盛ラベル付きの対数スケール "Log10" 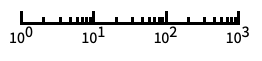
10のベキ乗に目盛が付いた,10を底とする対数スケール "SignedLog" 
0と負の数を含む対数に似たスケール "Reverse" 
座標の向きを逆にする "Infinite" 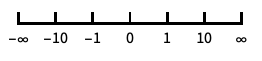
無限スケール - θ パラメータ空間あるいは ϕ パラメータ空間のスケーリングは,プロットのサンプリングに影響するが,全体的なプロットの外観には影響しない.
全オプションのリスト



例題
すべて開くすべて閉じるスコープ (18)
サンプリング (9)
関数が急速に変化するところではより多くの点がサンプルとして取られる:
PlotPointsおよびMaxRecursionを使って適応的サンプリングを制御する:
PlotRangeを使って関心領域に焦点を当てる:
Exclusionsを使って点の除去や結果の曲面の分割を行う:
ScalingFunctionsを使って x 軸の向きを逆にする:
プレゼンテーション (9)
各曲面にインタラクティブなTooltipを与える:
オプション (62)
BoundaryStyle (4)
BoundaryStyleは自動的にMeshStyleにマッチする:
曲面がRegionFunctionで切り取られた部分には境界が描かれる:
曲面がExclusionsで切り取られた部分には境界は描かれない:
ColorFunction (5)
EvaluationMonitor (2)
Exclusions (5)
Mesh (5)
MeshShading (7)
Noneを使って切片を取り除く:
MeshShadingはスタイリングに関してはPlotStyleより優先順位が高い:
MeshShadingをAutomaticに設定し,特定の部分にPlotStyleを使う:
MeshShadingはColorFunctionとともに使うことができる:
FaceFormを使って異なる曲面に異なるスタイルを使う:
NormalsFunction (3)
PlotLegends (3)
TextureCoordinateFunction (4)
特性と関係 (8)
SphericalPlot3DはParametricPlot3Dの特殊ケースである:
回転する曲面と円柱座標にRevolutionPlot3Dを使う:
三次元の任意の曲線と曲面にParametricPlot3Dを使う:
極座標の曲線にPolarPlotを使う:
二次元の曲線と範囲にParametricPlotを使う:
ContourPlot3DとRegionPlot3Dを陰的に定義された曲面と範囲に使う:
ListPlot3DとListSurfacePlot3Dをデータに使う:
球の生成にSphereを使う:
テキスト
Wolfram Research (2007), SphericalPlot3D, Wolfram言語関数, https://reference.wolfram.com/language/ref/SphericalPlot3D.html (2022年に更新).
CMS
Wolfram Language. 2007. "SphericalPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/SphericalPlot3D.html.
APA
Wolfram Language. (2007). SphericalPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SphericalPlot3D.html