SystemModelUncertaintyPlot[sys,spec]
plots the uncertainty in outputs in the system model sys from uncertainty in inputs according to spec.




SystemModelUncertaintyPlot
SystemModelUncertaintyPlot[sys,spec]
plots the uncertainty in outputs in the system model sys from uncertainty in inputs according to spec.
Details and Options





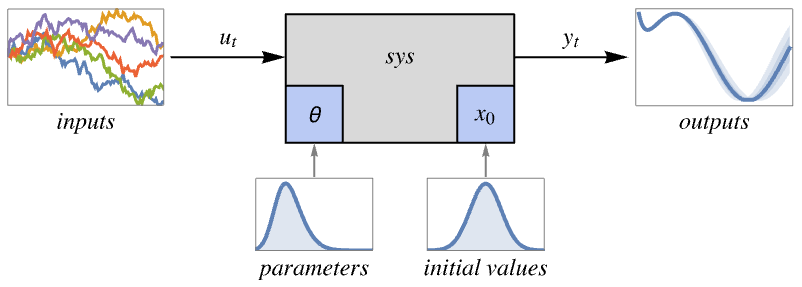
- SystemModelUncertaintyPlot is typically used to visualize the uncertainty of key signals in a system model resulting from uncertainty in parameters, initial values or inputs. This allows for graphical validation of the impact of uncertainties.
- Given the uncertain parameters, initial values and inputs, the system is simulated a large number of times and a slice function is applied at every point in time to compute aggregate statistics. By default, quantiles are used as a slice function.
- The system model sys can have the following forms:
-
SystemModel[…] general system model StateSpaceModel[…] state-space model TransferFunctionModel[…] transfer function model AffineStateSpaceModel[…] affine state-space model NonlinearStateSpaceModel[…] nonlinear state-space model DiscreteInputOutputModel[…] discrete input-output model - spec is an Association that allows the following keys:
-
"InitialValues" {v1val1,…} variable vi has initial value vali "Inputs" {in1fun1,…} input ini has value funi "Outputs" {v1,…} variables to plot "ParameterValues" {p1val1,…} parameter pi has value vali "SimulationCount" 200 target number of simulations "SimulationInterval" {tmin,tmax} simulate and plot from time tmin to tmax "SliceFunction" sfun function to compute for each time slice - When multiple sources of uncertainty are provided, simulations are performed covering their combinations, using the target number of simulations as an upper bound.
- The values vali in "ParameterValues" and "InitialValues" can take the following forms:
-
pval a single value {pval1,…} custom list of values randomly sampled int an Interval or CenteredInterval uniformly sampled dist an Around or a distribution to sample reg a region to sample uniformly - Multidimensional regions and distributions vald for sets of d variables can be set with {v1,…,vd}vald.
- The inputs funi in "Inputs" can take the following forms:
-
f a single function f[t] at time t {f1,…} a custom list of functions randomly sampled rproc a random process to sample - Vector-valued functions and processes fund for sets of d inputs can be set with {in1,…,ind}fund.
- The slice function sfun can take the following forms:
-
"MinMax" min and max "Quantiles" quantiles 0%, 25%, 50%, 75%, 100% {"Quantiles",{q1,…}} quantiles {q1,…} "Confidence" mean and 95% confidence bands {"Confidence",{cl1,…}} confidence bands with confidence levels {cl1,…} {sfun1,…} list of custom scalar-valued functions - SystemModelUncertaintyPlot has the same options as ListLinePlot, with the following additions and changes: [List of all options]
-
AxesLabel Automatic indicate units on the axis Filling Automatic filling to insert under each curve FrameLabel Automatic frame labels Method Automatic what simulation and plot methods to use PlotLabel Automatic overall label for the plot PlotLayout Automatic how to position data PlotLegends Automatic legends for curves ProgressReporting $ProgressReporting control display of progress SamplingPeriod Automatic sample period for random processes TargetUnits Automatic - units to display in the plot
- Method settings take the form Method <|"sub1"val1,…|>.
- Method suboptions "subi" include:
-
"PlotMethod" Automatic plot method "SimulationMethod" Automatic simulation method - "PlotMethod" settings are the same as the Method settings in ListLinePlot.
- "SimulationMethod" settings are the same as the Method settings in SystemModelSimulate.
- SystemModelUncertaintyPlot uses the output as a plot label in the default PlotLayout.
- With PlotLayout "Association", SystemModelUncertaintyPlot gives an Association with the output as the key and its corresponding plot as the value for each requested variable.
- Possible settings for TargetUnits include:
-
None no unit "Unit" unit defined in model "DisplayUnit" display unit defined in model (default) unit explicit unit {unitt,unit} units for time and data - Models with "Epoch" in their simulation settings trigger the use of DateScale.
-
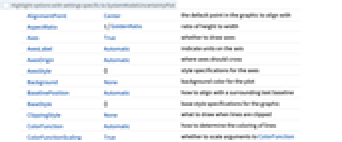
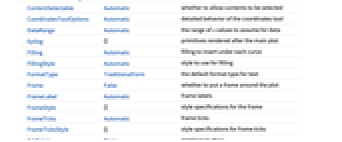
AlignmentPoint Center the default point in the graphic to align with AspectRatio 1/GoldenRatio ratio of height to width Axes True whether to draw axes AxesLabel Automatic indicate units on the axis AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ClippingStyle None what to draw when lines are clipped ColorFunction Automatic how to determine the coloring of lines ColorFunctionScaling True whether to scale arguments to ColorFunction ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DataRange Automatic the range of x values to assume for data Epilog {} primitives rendered after the main plot Filling Automatic filling to insert under each curve FillingStyle Automatic style to use for filling FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel Automatic frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic InterpolationOrder None the polynomial degree of curves used in joining data points IntervalMarkers Automatic how to render uncertainty IntervalMarkersStyle Automatic style for uncertainty elements LabelingFunction Automatic how to label points LabelingSize Automatic maximum size of callouts and labels LabelStyle {} style specifications for labels MaxPlotPoints Infinity the maximum number of points to include Mesh None how many mesh points to draw on each line MeshFunctions {#1&} how to determine the placement of mesh points MeshShading None how to shade regions between mesh points MeshStyle Automatic the style for mesh points Method Automatic what simulation and plot methods to use MultiaxisArrangement None how to arrange multiple axes for data PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotHighlighting Automatic highlighting effect for points PlotLabel Automatic overall label for the plot PlotLabels None labels for data PlotLayout Automatic how to position data PlotLegends Automatic legends for curves PlotMarkers None markers to use to indicate each point PlotRange Automatic range of values to include PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to determine the style of each line PlotTheme $PlotTheme overall theme for the plot PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic ProgressReporting $ProgressReporting control display of progress Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame SamplingPeriod Automatic sample period for random processes ScalingFunctions None how to scale individual coordinates TargetUnits Automatic - units to display in the plot
Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks

List of all options




Examples
open all close allBasic Examples (1)
Scope (20)
Models (4)
Plot uncertainty in two variables of a SystemModel:
Plot the uncertainty in the output of an AffineStateSpaceModel:
Plot the uncertainty in the output of a NonlinearStateSpaceModel:
Plot the uncertainty in the output of a DiscreteInputOutputModel:
Use a SquareWave input:
Specification (4)
Uncertainty in Values (5)
Plot the uncertainty generated from giving a list of values for a parameter:
Plot the uncertainty generated from sampling an interval for a parameter value:
Plot the uncertainty generated from sampling a distribution for a parameter value:
Plot the uncertainty generated from sampling a geometric region for a parameter value:
Plot the uncertainty generated from sampling a Circle for two initial values:
Uncertainty in Inputs (3)
Plot the uncertainty generated when an ARIMAProcess is used for an input:
Plot the uncertainty generated when several functions are used as input:
Use these profiles for the input flow rate in a continuous stirred tank reactor:
Plot the uncertainty generated when using a two-dimensional process for two inputs:
Options (17)
AxesLabel (2)
Filling (2)
FrameLabel (2)
Method (1)
Set a custom simulation method with Method:
PlotLayout (2)
PlotLegends (2)
ProgressReporting (1)
Control progress reporting with ProgressReporting:
ScalingFunctions (2)
Plot the model with log-scaled values using ScalingFunctions:
Models with "Epoch" in its simulation settings are plotted as values at a sequence of dates:
Use ScalingFunctions{None,Automatic} to produce simulation time plots instead:
Use DateTicksFormat to format for date tick labels:
TargetUnits (1)
Set custom units with TargetUnits:
Applications (4)
Trajectories Near Equilibrium (1)
Plot the uncertainty in the angle and angular velocity of a simple damped pendulum when the initial conditions take values near equilibrium points:
When the system starts at rest at small angles, it evolves toward the stable ground position:
When the system starts near the unstable fully inverted position, it also evolves toward the ground position:
System Tolerance (1)
The performance of a circuit depends heavily on its components and parameter tolerances. When the resistance of one of the components in this model of a speaker follows a truncated normal distribution, the variation in the current going through the speaker can be measurable:
External disturbances can also affect the performance of a circuit. For instance, the input voltage of the speaker can be affected by high-frequency signals:
Plot the uncertainty in the current of the speaker when affected by these high-frequency disturbances:
Validation of Controlled Systems (1)
Validate a controlled ball and beam system by placing the ball away from the stable position:
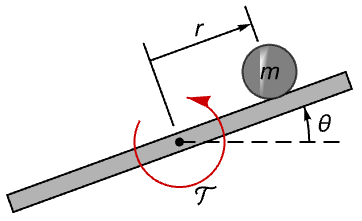
The farther away the ball starts from the equilibrium point, the more the system will struggle bringing it back to the stable position:
The control effort peaks at the start and then later a few more times to stop the ball from overshooting the stable position:
Controlled systems should also be validated against external disturbances. Stress the controlled ball and beam system with a white noise torque disturbance and plot the control effort as the system experiences various sampling periods of the noise:
Orbital Maneuver (1)
Study the effect of a short-time tangential boost on a toy spacecraft in a circular orbit:
Boosts of large magnitude can lead to unbounded trajectories:
Bounded or unbounded trajectories can unfold if the magnitude of the boost follows a normal distribution. Plot the uncertainty in the distance to the center of force:
Properties & Relations (2)
Use SystemModelPlot to plot individual curves:
Use SystemModelPlot to plot individual curves when doing a parameter sweep:
Use SystemModelPlot to plot sensitivity bands computed with SystemModelSimulateSensitivity:
Use SystemModelUncertaintyPlot to plot uncertainty:
Interval and CenteredInterval are sampled as regions:
Around and VectorAround are sampled as their corresponding distributions:
Related Guides
Related Links
History
Text
Wolfram Research (2024), SystemModelUncertaintyPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelUncertaintyPlot.html.
CMS
Wolfram Language. 2024. "SystemModelUncertaintyPlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemModelUncertaintyPlot.html.
APA
Wolfram Language. (2024). SystemModelUncertaintyPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemModelUncertaintyPlot.html
BibTeX
@misc{reference.wolfram_2025_systemmodeluncertaintyplot, author="Wolfram Research", title="{SystemModelUncertaintyPlot}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelUncertaintyPlot.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_systemmodeluncertaintyplot, organization={Wolfram Research}, title={SystemModelUncertaintyPlot}, year={2024}, url={https://reference.wolfram.com/language/ref/SystemModelUncertaintyPlot.html}, note=[Accessed: 17-January-2026]}