式の評価
| 評価の原理 | ループと制御構造体 |
| 式の標準形への還元 | 評価中に式を集める |
| 属性 | 評価処理のトレース |
| 標準評価手順 | 評価処理用スタック |
| 非標準な評価手順 | 無限評価の防止 |
| パターン，規則，定義の評価 | 処理の中断と放棄 |
| 反復関数における評価 | 式のコンパイル |
| 条件子 |
例えば，Wolfram言語は整数の加法用の組込み関数を使い，式6+7を評価する．同じように，簡約化のための組込み関数を使い，代数式x-3x+1を評価する．その際に，x=5との定義がすでに作成されていれば，Wolfram言語は，この定義を使いx-3x+1を-9に約す．
Wolfram言語において最も中心をなす2つの概念は「式」と「評価」であろう．「式」で説明したように，Wolfram言語が扱うオブジェクトは多岐に渡るが，それらのすべては，「式」を使い一様な形式で表される．ここでは，Wolfram言語が実行できるすべての操作を評価処理の例としてどのように統一的に見ることができるかを説明していく．
Wolfram言語は，既知の定義を適用し尽くした時点で，得られた式をそれがどのようなものであれ結果として返す．場合によっては，結果は数等のオブジェクトである．しかし通常は，シンボル形式で表されたいくつかのオブジェクトを含む式である．
Wolfram言語は，結果が変化しなくなるまで定義を適用していく，という原則に従う．このため，Wolfram言語が出力する最終結果を取り出し，再入力すると，同じ結果が再び得られる．（これに該当しない場合もある．詳しくは「無限評価の防止」を参照のこと．）
どんなときでも，Wolfram言語は，その時点で既知の定義しか使うことができない．もちろん，定義が後で追加されると，Wolfram言語はそれらも使うことができるようになる．ただし，その場合の結果は以前のものとは異なることもある．
最も単純な評価の例として，f[x_]=x^2等の定義を使って，式を直接他の式に変換するという処理がある．しかし，Wolfram言語で書かれたプログラムの実行に使われる処理も評価の形態である．したがって，例えば，条件子やループを含んだ一連のWolfram言語式で構成された手続き型のプログラムがあるとき，それを実行することは式を評価することに相当する．場合によっては，評価処理は，例えば，ループにおいて特定の式を何回も評価することもある．
例えば，関数Plusに関する組込み定義は，標準形に従った項を丸カッコでくくらない形式で加法の項を書くように設定されている．加法の結合則によると，(a+b)+cとa+(b+c)とa+b+cは等しい．しかし，多くの用途では，これらの項すべてが単一標準形a+b+cに還元された方が便利である．Plusの組込み定義はこの変形操作を行うように設定されている．
Plusに関する組込み定義を介すことで，この式は丸カッコなしの標準形に還元される：
足し算のような関数には結合則の他に交換則も成り立つため，a+c+bとa+b+cのように項の順序を入れ替えても値は等しいまま保持される．しかし，Wolfram言語では，このような式はすべて一律な「標準形」にされる．ここで，使われる標準形とは，すべての項を，アルファベット順に近い並び順に対応した一定の順序に置く形を言う．
上の例で，項を可能な限りの並び順に変え，2つの構成を見比べることでa+c+bとc+a+bが等しいかどうかを判断するのは可能である．しかし，そうするよりは，両方の式を標準形にしてから判定した方が処理能率はよくなる．
例えば，多項式には2つの標準形が考えられるが，それぞれ違った目的に適する．その1つは，Expandを作用させることで得られる展開された項の単純和である．この標準形は多項式の加減法を行うのに最適な形である．
多項式の標準形はもうひとつある．Factorを適用することで，多項式を，それ以上は還元できない因数で作られた積として書くことができる．この標準形は除法等の演算に適している．
展開形と因数分解形はどちらも同等に重要な多項式の標準形である．どちらを使うかは，何にそれを適用させるかによる．このため，Wolfram言語では，多項式は，自動的にこれらの形のいずれかに変換されるということはない．その代りに，ExpandとFactor等の関数が提供されているので，それらを使うことで，ユーザ自身が多項式の形を明示的に選択することができるようになっている．
単にExpandを作用させるだけで展開形に変形させることができる．2つの式が等しいことが明白になる：
この疑問に関する基本結果は数学の計算理論からすでに判明している．それによると，標準形に還元することは式によっては不可能である．2つの任意の式があるとき，限られた変換操作でこれらを標準形に整理できるという保証はない．
このことは，ある意味では，あまり驚くようなものでもない．どんな式でも標準形に直せるなら，式が等しいかどうかは簡単に判明させることができてしまう．しかし，数学の難解問題には，いわゆる式の同値性に関するものが数多くある．この事実からも，変換操作がいかに難しいものかが分かる．
関数の性質は，属性で指定することができる．例えば，Flatと呼ばれる属性を関数に付与しておくと，その関数は「平坦」な特性を持つことになる．つまり，引数の部分がネストすれば，自動的にそのネスト部が平坦化され，結合則が適用可能な状態になる．
Flatのような属性は評価の仕方だけでなくパターンマッチ等の操作にも影響する．このため，属性の指定は，関数を定義したり，変換規則を適用する前に行う必要がある．
| Attributes[f] | f の属性を参照する |
| Attributes[f]={attr1,attr2,…} | f に複数の属性を一括で割り当てる |
| Attributes[f]={} | f を属性なしとする |
| SetAttributes[f,attr] | 属性 attr を f に加える |
| ClearAttributes[f,attr] | f の属性 attr を除去する |
| Orderless | 交換則が適用する関数とする（引数は標準的順序に並び替る） |
| Flat | 結合則が適用する関数とする（引数は平坦化される） |
| OneIdentity | 関数をパターンマッチング用の引数の値に等しいとする（例：f[f[a]]は a に等しい） |
| Listable | f は引数であるリストの各要素に同じ関数を適用した関数とする （例：f[{a,b}]は{{f[a],f[b]})となる） |
| Constant | f のすべての階の導関数がゼロの関数とする |
| NumericFunction | f は，引数を数値とすれば，関数の返す値も数値になるような特性を持つ関数とする |
| Protected | f の値は変更不可 |
| Locked | f の属性は変更不可 |
| ReadProtected | f の値は参照不可 |
| HoldFirst | f の第1引数は評価不可 |
| HoldRest | f の第1引数を除くすべては評価不可 |
| HoldAll | すべての f の引数は評価不可 |
| HoldAllComplete | f の引数は完全に不活性なものとする |
| NHoldFirst | f の第1引数はNによる数値計算不可 |
| NHoldRest | f の第1引数を除くすべてはNによる数値計算不可 |
| NHoldAll | すべての f の引数はNによる数値計算不可 |
| SequenceHold | |
| Temporary | f は不必要になると除去される局所変数として扱われる関数とする |
| Stub | f が明示的に入力されたときにはNeedsが自動的に呼び出される |
組込み関数Plusがどんな属性を持っているか調べる：
Wolfram言語の組込み数学関数に割り当てられている重要な属性にListable（リスト可）がある．この属性の関数に引数をリストとして与えると，関数頭部がリストの各要素に直接かかるように適用される．「糸を縫う」ように各リスト要素に分配されることから，この分配操作は英語でスレッド(thread)とも呼ばれる．
多くの属性は，適用先の関数の評価そのものに直接影響を与える．評価には影響しないが，他の面で影響を与える属性もある．例えば，属性OneIdentityはパターンマッチだけに影響する（「平坦な関数と順不同な関数」を参照）．同様に，属性Constantは微分を計算するときか，微分に依存する操作が必要なときだけに有効になる．
属性Protectedは割当て操作に影響する．プロテクトの掛かったシンボルは再定義することができない．「組込み関数の変更」で説明した関数ProtectとUnprotectを，SetAttributesとClearAttributesの代りに使っても，プロテクトの有効化と解除を行うことができる．「組込み関数の変更」で触れたが，Wolfram言語が起動した時点では，ほとんどの組込み関数にプロテクトが掛かっている．このため，ユーザが誤って定義付けをしようとしてもできない．
特定のシンボルに割り当てた定義を参照するには?f と入力する（組込み関数にもこれに関連した機能を提供するものが各種あるので，それらを使ってもよい）．参照禁止の属性ReadProtectedを変数や関数に付加しておけば，定義内容が参照できないようにすることができるようになっている．参照不可になっても，関係式自体は有効なままであり，引き続き評価に使うことができる．
SetAttributesやClearAttributesのような関数を使えば，通常，変数や関数の属性をどのようにでも設定変更することができる．ただし，あらかじめ変数や関数に属性Lockedが割り当ててあるときは，属性の変更はできない．（新たに設けたWolframシステムセッションなら，ロックは解除されるので，この限りではない．）属性Lockedを属性Protectedと参照禁止の属性ReadProtectedに組み合せて使うことで，ユーザによる不用意な定義内容の参照や，変更を未然に防ぐことができる．
関数に属性を与えるということは，Wolfram言語に対して評価や参照で特別な性質を考慮するよう指示することを意味する．通常，一度与えられた性質は常に有効だが，場合によっては，限られた状況下でだけそれを有効にしたいかもしれない．そのようなときは，属性は直接使わずに，代りに，特殊な関数を呼び出すことでその属性に関連付けられた変換を行うことも可能である．
| Function[vars,body,{attr1,…}] | 属性 attr1, … を備えた純関数を定義する |
Wolframシステムは，式の頭部を評価し終えると，即座に頭部が属性を持ったシンボルかどうかを判定する．もしも，順不同性Orderlessや平坦性Flat，または，リスト可Listableの属性が備わっていると，Wolframシステムは，式の要素の評価が終了した時点で，これらの属性に関連した変換操作を行う．
「評価の原理」で説明したが，Wolframシステムにおける評価の基本は，適用可能な規則がなくなるまで式の評価を続ける，ということである．つまり，結果が出たら，それに対して再び規則が適用される．そして，次の結果に変化がなくなるまで，評価処理は繰り返される．
| 2ax+a^2+1 | ユーザが式を入力する |
| Plus[Times[2,a,x],Power[a,2],1] | 式が内部表記に変換される |
| Times[2,a,x] | まずこの項が評価される |
| Times[2,7,x] | aが評価され，あらかじめ定義された値7が代入される |
| Times[14,x] | 式全体にTimesの組込み定義が使われ，積が評価される |
| Power[a,2] | この項が次に評価される |
| Power[7,2] | aに割り当てられた値7が代入される |
| 49 | 式全体にPower用の組込み規則が使われ，ベキが計算される |
| Plus[Times[14,x],49,1] | 評価済みの各項がPlus式に取り込まれる |
| Plus[50,Times[14,x]] | 式全体にPlus用の組込み定義が使われ，和が計算される |
| 50+14x | 結果がこのように表示される |
「評価処理のトレース」で触れるが，Wolframシステムにはトレースと呼ばれる評価処理の追跡機能が備わっている．Trace[expr]を式に作用させると，式の評価過程で生成される暫定的な内部式をネストされたリスト形式で表示することができる．（注意点として，標準評価手順では，式の木構造において最下位から上位に向かって評価は進められるので，式の最小単位の部分がTraceからの結果のリストに最初に現れる．）
定義の適用順序は重要な意味を持っている．つまり，「組込み関数の変更」で触れたように，ユーザ指定の定義は組込み型の定義より優先されるため，組込み型の定義を代替するための定義を与えることが可能である．
この式の評価には，ArcSinの組込み定義が使われる：
ArcSinにユーザ指定の定義を与える．プロテクトを解除しておく必要がある：
「異なるシンボルへの定義式の関連付け」で説明したが，規則を上向きの値または下向きの値としてオブジェクトに割り当てることができる．Wolframシステムは，上向きの値の定義を下向きの値の定義より優先させる．
f[g[x]]のような式には，通常，適用可能な定義には2つの形式がある．f に関連付けられた下向きの値，そして，g に関連付けられた上向きの値である．Wolframシステムは，g に関連付けられた定義を f の定義より優先させる．
この順序付けは，特殊な規則は一般的な規則より先に適用させる，といった指針に基づいている．関数に関連付けられた下向きの値の前に，引数に関連付けられた上向きの値を優先させることで，任意の引数を持つ関数のための一般定義を上書きする特別な引数に対する定義を作成することができる．
Plusのような組込み関数の多くは下向きの値を持つ．ただし，Wolframシステムの組込み型オブジェクトによっては上向きの値を持つものもある．例えば，ベキ級数を表すのに使われるSeriesDataオブジェクトは，数学的操作に関した組込み済みの上向きの値を持つ．
- g に関連付けしたユーザ定義
- g に関連付けられている組込み定義
- f に関連付けしたユーザ定義
- f に関連付けられている組込み定義
下向きの値より上向きの値の方が優先されるという事実は，いろいろな場面で重要な意味を持つ．例えば，式を再構成するための操作を定義するとする．再構成の操作に関する上向きの値を各種オブジェクトに対して与えると，これらの上向きの値はこのオブジェクトが現れるたびに使われる．しかし，特別なオブジェクトが見当たらないときに使うための，再構成用の一般的な手続きを与えることもまた可能である．その場合，この手続きは，再構成操作に関する下向きの値として与えることができる．下向きの値は上向きの値の後に試されるので，上向きの値を伴ったオブジェクトが何もないときに限って，一般手続きが使われる．
一般に，式は上向きの値を備えた複数のオブジェクトを持つ．Wolframシステムは，まず，式の頭部を参照し，それに関連した上向きの値を試す．次に，式の各要素を順々に参照していき，要素に上向きの値があればそれを試す．この手順は，まずユーザ定義の上向きの値に対して行われ，続いて，組込み済みの上向きの値に対して行われる．また，この手順が一連の要素に対して適用されるとき，先に現れる要素に関連付けられた上向きの値は，後寄りの要素に関連付けられた上向きの値より優先される．
組込み関数のほとんどは標準的な評価手順に従って評価されるが，例外もある．例えば，プログラムの構築や実行に使われるほとんどの関数は，非標準の手順で処理される．このような関数では，引数の一部が全く評価されなかったり，引数は評価されても関数の制御下にあるため特別処理を受けたりするものもある．
| x=y | 式の左辺は評価しない |
| If[p,a,b] | |
| Do[expr,{n}] | expr を n 回繰返し評価する |
| Plot[f,{x,…}] | x の数値データについて式 f を評価する |
| Function[{x},body] | 実際に関数の適用があるまでは評価しない |
a=1のような定義を与えるとき，左辺に現れる a は評価されない．評価されると，困った状況に陥るだろう．なぜかといえば，例えば，先に a=7と割り当てておき，後で，a=1と直すと，前の定義が a に適用されてしまい，定義が7=1と無意味な形になってしまう．
標準評価手順において，関数の引数は式の先頭のものから順々に評価される．この処理を強制的に禁止するには，HoldFirst，HoldRest，HoldAllの式の評価を保留にする属性を式に設定しておく．
関数にホールド属性が付いていて，引数が評価保留の状態にあっても，Evaluate[arg]を引数に作用させることで強制的に評価を行うことができる．
| f[Evaluate[arg]] | f にホールド属性があっても，引数 arg を強制的に評価する |
ホールド用の属性と強制評価の関数を組み合せることで，関数の引数評価をいつ実行したらよいかを制御することができる．引数にEvaluateを作用させておき，関数が参照されるのを待たずに，即座に評価させることも可能である．この方法はいろいろな場面で便利になる．
普通は，式を入力したら，そのすべてを評価したい．それでも，場合によっては，式を評価処理から外しておきたいときもあるだろう．例えば，Wolfram言語プログラムにおいて式のある部分にシンボル的な操作を施したいとする．そのようなとき，この操作が行われる間は評価保留にしておきたい．
Hold[expr]とHoldForm[expr]の違いは出力における表示的なものである．標準出力表記では，Holdの記述は表示されるが，HoldFormは表示されない．完全形に切り換えれば，両方とも表示される．
Holdを作用させると，式は未評価の形のまま保持される：
HoldFormも評価保留にできる．しかし，標準形的なWolfram言語の出力形式では表示されない：
完全形にすると，HoldFormの使用が確認できる：
| Hold[expr] | 式 expr の評価を保留にする |
| HoldComplete[expr] | 式 expr の評価を保留にし，expr に関連付けられている上向きの値の適用を防止する |
| HoldForm[expr] | 式 expr の評価を保留にし，HoldFormは記述せずに表示する |
| ReleaseHold[expr] | |
| Extract[expr,index,Hold] | 式 expr の一部をHoldで包み込み，評価されないようにする |
今度は，抽出した部分をHoldで包み込み，評価不可にする：
| f[…,Unevaluated[expr],…] | 式 expr 未評価のまま引数として f に与える |
| SequenceHold | 引数として現れるSequenceオブジェクトは平坦化しない |
| HoldAllComplete | 全引数を完全に不活性なものとする |
全引数のホールド属性HoldAllを与えることで，関数の引数をすべて評価不可にすることができる．しかし，この属性を与えても，引数の変換処理が一部実行されてしまう．つまり，評価保留にする引数がSequenceオブジェクトのときは，平坦化処理が行われてしまう．これを禁止にするには，SequenceHoldの属性を適用する必要がある．また，引数に上向きの値が関連付けられていると，上向きの値が適用されてしまう．これを防ぐには，属性HoldAllCompleteを与えておき，評価禁止関数Unevaluatedが除去されないようにしておく必要がある．
式の評価とパターンマッチングの処理では，いくつかの相互作用的な操作が必要になる．第一に，パターンマッチングでは，検索の対象となる式は少なくとも部分的に評価済みである．このため，パターン自体もあらかじめ評価しておいた方が都合がよい．
場合によっては，パターンの全部もしくは一部を評価不可としておきたい．そうするには，HoldPatternを評価不可にしたい部分に作用させる．つまり，評価したくないパターンが patt ならば，HoldPattern[patt]と記述する．すると，パターンとしての patt の機能はそのまま保持されるが，パターン自体は未評価のままになる．
| HoldPattern[patt] | パターンマッチングの機能上は patt と同じだが，patt では評価は保留にする |
HoldPatternの応用ケースとして，まだ評価されていない式，つまり未評価の形の式に対して適用するためのパターンの指定がある．
上の例で示したように，通常，lhs->rhs のような変換規則において左辺 lhs はすぐに評価されてしまう．規則は，普通，すでに評価済みの式に対して適用されるからである．また，lhs->rhs における右辺もすぐに評価される．ただし，遅延型の規則 lhs:>rhs を使えば，右辺 rhs は評価しないまま保持しておくことができる．
変換規則の左辺は普通評価されるが，定義の左辺は普通評価されない．理由は次の通りである．変換規則は，通常，/.を介して評価済みの式に適用される．これに対して，定義は評価の過程で適用される．つまり，まだ完全に評価の済んでいない式に適用される．定義をこのような式に対して適用可とするには，定義の左辺を少なくとも一部未評価のまま保持しておく必要がある．
最も単純なケースとして，シンボルに対する定義がある．「非標準な評価手順」で説明したが，x=value の定義において，左辺にあるシンボルは評価されないまま残される．もしも，定義が与えられる前に，x に y が割り当てられ，その上で，x=value により左辺が評価されることになったなら，y=value といったおかしな定義が発生してしまう．
定義の左辺にある個々のシンボルは評価されないが，左辺が複雑な式からなるときは，それらが部分的に評価されることもある．例えば，左辺が f[args]のような形を取るとき，引数部 args は前もって評価される．
定義の左辺に現れる関数において，その引数部を先に評価しなければならない理由は，ある式の評価においてこの定義がどう使われるかを考えるとよく分かる．「評価の原理」で説明したように，関数が評価されるときは，関数の持つ引数がまず評価の対象になる．その次に，関数に関連した定義が検索され，見付かればそれが適用される．つまり，定義を関数に適用する前に，引数はすでに評価済みでなければならない．ただし，例外が1つある．それは，対象となる関数が特別な属性を備えており，引数の評価が保留になっているときである．
| symbol=value | 変数 symbol は評価しないが，値 value は評価する |
| symbol:=value | 変数 symbol と値 value はともに評価しない |
| f[args]=value | 引数 args は評価するが，左辺全体は評価しない |
| f[HoldPattern[arg]]=value | 引数 arg の評価なしで f[arg]が割り当てられる |
| Evaluate[lhs]=value | 左辺を完全に評価する |
定義の左辺に現れる関数において，その引数が先に評価されることは，普通，適切である．しかし，状況によっては，そうしたくない場合もある．そのようなときは，評価不可としたい部分に対してHoldPatternを作用させておく．
Table[f,{i,imax}]等の評価で取られる最初のステップでは，i の値を局所的にすることが行われる（「ブロックと局所値」を参照のこと）．次に，反復回数の上限 imax が評価される．式 f は，i の値が確定するまで未評価なまま保持される．反復評価がすべて終了したとき，変数 i にはもとの大域値が戻される．
乱数生成関数RandomReal[]を4回実行する．毎回，別の擬似乱数が生成される：
Table[f,{i,imax}]のような反復式では，普通，i に特定の値が割り当てられるまでは関数 f は未評価な形のままにしておいた方がよい．任意の値を持つ i に対して有効となる関数 f の完全なシンボル形式が見付からないときは特にそうである．
Table[f,{i,imax}]のような式において，f を，任意な i を持つ関数として完全なシンボル形式で記述することが可能であれば，このシンボル形式をまず計算してしまい，その後にTableを作用させた方が計算の効率が上がる．これを行うには，Table[Evaluate[f],{i,imax}]を使う．
| Table[f,{i,imax}] | i に特定な値が割り当てられるまでは f を未評価なままにしておく |
| Table[Evaluate[f],{i,imax}] | i は未知数としておいて，f を強制的に評価する |
| lhs:=rhs/;test | 判定式 test の評価結果がTrueのときだけ定義を有効にする |
| If[test,then,else] | |
| Which[test1,value1,test2,…] | 判定式 testi を順に評価していき，最初にTrueになる判定式に対応した値を返す |
| Switch[expr,form1,value1,form2,…] | 式 expr を形 formiと比較していき，最初にマッチする形に対応した値を返す |
| Switch[expr,form1,value1,form2,…,_,def] | 値 def をデフォルト値として使う |
| Piecewise[{{value1,test1},…},def] | Trueを与える最初の testi に当たる値を返す |
Wolfram言語によるプログラムの記述で分枝制御を行うには基本的に2つの方法を使う．1つ目は，単一定義を作り，右辺にIf関数による選択肢を与える方法で，2つ目は，複数の定義を作り，各定義を適切な/;条件で制御する方法である．複数の定義を使った方が，プログラムを読みやすくでき，変更も簡単になる．
選択肢が2つありどちらかを選択するには関数Ifを使うことができる．しかし，選択肢がさらにある場合もある．そのようなときの方法として，ネストさせた複数のIf関数を使うことが考えられる．しかし，普通は，WhichやSwitch等の関数を使う方がよい．
3つの定義域を持つ関数を定義する．第3条件をTrueとすることで，第1と第2定義域に入らないときのデフォルトを与えておく：
これにはWhichの第1ケースが使われる：
これは重要なことだが，Wolfram言語のようなシンボル式の処理システムでは，条件によってはTrueにも，Falseにもならないことがある．したがって，例えば，条件x==yでは，xとyの両方の数値的な値が判明しない限りTrue，Falseの判定は付かない．
| If[test,then,else,unknown] | |
| TrueQ[expr] | |
| lhs===rhs あるいは SameQ[lhs,rhs] | |
| lhs=!=rhs あるいは UnsameQ[lhs,rhs] | |
| MatchQ[expr,form] |
lhs===rhs と lhs==rhs の間には次の大きな相違点がある．前者は常にTrueかFalseを返すが，後者はシンボル形式のまま入力を残すことがある（「方程式」を参照）．===は式の構造を判定したいときによく使われ，==は数学的な等しさを判定したいときに使う．パターンマッチを行うWolfram言語の制御部では，実効的な===の機能が使われ，ある式が別の式に記述通りにマッチするかどうかが判断される．
条件子の設定において，test1&&test2&&…のような組合せ条件を使う必要がよくある．この組合せ条件で重要な点は，条件項目 testi でFalseとなるものがひとつでもあると判定結果はFalseになる，という点である．Wolfram言語は，条件項目 testi を1つずつ評価し，testi のいずれかがもFalseになると，その時点で判定を打ち切る．
| expr1&&expr2&&expr3 | 条件式 expri を1つずつ評価していき，ひとつでもFalseになれば評価を打ち切る |
| expr1expr2expr3 | 条件式 expri を1つずつ評価していき，ひとつでもTrueになれば打ち切る |
Wolfram言語では，先の条件が満たされなければ後の条件は満足されないとする複数条件を並べた論理式を構築することができる．同様な処理手順がC言語のような言語でも見られるが，うまく利用すると各種プログラムを構築する上で便利になる．
Wolfram言語プログラムの実行とは，一連のWolfram言語式の評価を意味する．単純なプログラムでは，式はセミコロンで区切られ，1つずつ評価されることが多い．しかし，多くの場合は，式を繰り返し評価する必要があり，ある種の「ループ」を使う必要が出てくる．
| Do[expr,{i,imax}] | 反復変数 i を刻み幅1で1から imax に増加させ，式 expr を繰り返し評価する |
| Do[expr,{i,imin,imax,di}] | 反復変数 i を刻み幅 di で imin から imax に増加させ，式 expr を繰り返し評価する |
| Do[expr,{i,list}] | i が list からの値を取って expr を評価する |
| Do[expr,{n}] | 式 expr を n 回評価する |
Do式の内部に手続きを入れることもできる：
| Nest[f,expr,n] | 関数 f を式 expr に n 回適用する |
| FixedPoint[f,expr] | 関数 f を繰り返して式 expr に適用し，結果の式が変化しなくなる時点で停止する |
| NestWhile[f,expr,test] |
Doを使えば，反復変数をいろいろな値に振り特定の式を評価することで一連の操作を繰り返すことが可能である．それでも，「関数を反復的に適用する」に示したような関数型プログラミングの構成体を使うと，分かりやすく，また，効率的なプログラムを記述することができる．例えば，関数Nest[f,x,n]を使えば関数を繰り返し，再帰的に式に適用する，ということが可能になる．
純関数をネストさせ，前述のDoの例で作った式と同じ計算をする式を作る：
このように，Nestは，関数を指定した回数だけ繰り返し適用するのに使う．それでは，関数を繰り返し適用させ，結果が変化しなくなったら自動的に停止させる，という処理を行いたい場合はどうするのか．そのときは，関数FixedPoint[f,x]を使い定常点の探索を行うようにすればよい．
FixedPointは，結果が変わらなくなるまで関数を繰り返し適用する：
関数FixedPointを使うことで，カーネルの評価プロセスそのものや，expr//.rules 等の関数操作をまねることができる．FixedPointでは，2回の逐次結果に変化がなくなるまで関数の適用が続けられる．一方NestWhileでは，任意の関数がTrueでなくなるまで続けられる．
ThrowとCatchを組み合せて使うと，Wolfram言語の評価プロセスを監視することができるため便利である．評価を監視したい式には，Catchを作用させておく．評価処理中にThrowが現れると，その時点で進行中の処理は停止し，それに与えられている引数の現行値が返される．
ThrowとCatchを使えば，関数的なプログラミング構成体における操作処理を特定条件が満たされるまで続行させ，満たされなくなった時点で中断させることができる．Throwで評価を中断すると，得られる結果は途中結果である．途中結果なので，式は，仮に最後まで評価を続けたときの式とは構成上多少違ってくることに注意してほしい．
Throwがないため，上の式と同じ結果が得られる：
関数を定義する．この関数は，引数に10より大きい値を入力した場合，Throwを発生させる：
Throwは起らない：
短いプログラムでは，Throw[value]とCatch[expr]の最も単純な書式を使うだけでよい．しかし，構成部分が増えプログラムが長くなると，Throw[value,tag]とCatch[expr,form]の書式を使った方がよいだろう．タグ tag と形 form を局所的なものとしておくことで，ThrowとCatchがプログラムの特定部分だけで機能するようにすることができる．
今度は，外側のCatchによりキャッチされる：
パターンでCatchの認識するタグを指定してもよい：
ここでの注意点は，Throwで使うタグは定数である必要はない．通常，それはどんな式であっても構わない．
Throw[value,tag]とCatch[expr,form]の書式を使った場合，Catchの返してくる値はThrowに指定した第1引数 value になる．また，Catchの書式をCatch[expr,form,f]にすると，f[value,tag]が返される．
構造化アプローチを取るなら，Do，Nest，FixedPoint等の関数を使いループを構築するとよい．また，ThrowとCatchを併せて使えば，ループを監視，制御することも可能である．一方，構造にとらわれないループを作りたい場合は，関数WhileやForを使うとよい．任意条件下で繰返し処理を停止できるループを構築することができる．
Whileループは，条件が満たされなくなるまで実行される：
WhileとForのループにおいて，まず評価されるのは条件式であり，その次に，本体の式が評価される．つまり，Trueにならなければその時点でWhileおよびForループは終了してしまう．このため，本体の式が評価されるのは条件式がTrueになるときだけである．
関数的な構成体では，制御フローが非常に単純である．WhileやForのループでは，制御フローがプログラム実行時の条件式の値に左右されてしまうので，ループが複雑な構成になりがちである．とは言え，ループであっても，制御フローは，普通その本体で与えられた式の値に依存するようなことはない．
それでも，場合によっては，本体の式の値に依存した形でフローを変えてやらなければならない．これを行う方法として，まず，関数的なプログラミングの考え方に適合した手法，つまり，関数ThrowとCatchを使う方法が考えられる．さらに，Wolfram言語にはC言語で提供される制御フローの操作用関数に相当した各種の関数が用意されているので，それらを利用するのも便利である．
| Break[] | 最も近いレベルにあるループから退避する |
| Continue[] | 現行ループの次のステップに進む |
| Return[expr] | 関数から値 expr を返す |
| Goto[name] | 現行手続きにあるLabel[name]位置にジャンプする |
| Throw[value] | 制御を戻し，Catchの戻り値として値 value を返す（非局所的なリターン） |
Return[expr]を使い，戻り値を指定することも可能である．ネストされた関数式から一挙に退避できることから，Throwを非局所的なリターン機能と考えることもできる．エラー処理に利用すると便利である．
引数が5より大きいので，手続きでは最初のReturnが使われる：
実行してもThrowに制御は移らない：
Continue[]やBreak[]の関数はループの始点もしくは終点に制御を移すために使う．場合によっては，ループの外にある手続き内の任意の位置に制御を移したい．そのようなときは，転送先を関数Labelであらかじめラベル指定をしてから関数Gotoを使い実際に制御を移す．
注意してほしいが，Gotoを使うには同じ手続き内にLabel指定がなければならない．ただし，Goto指定を使うとフロー構造が入り組んだものになり，プログラムがどう機能しているのか分かりづらくなるので使用には注意が必要である．
Sowできる関数を定義する：
| Sow[val,tag] | 刈り取るときを示したタグを付けて val を播く |
| Sow[val,{tag1,tag2,…}] | 各タグ tagi に val を播く |
| Reap[expr,form] | タグが form にマッチするすべての値を刈り取る |
| Reap[expr,{form1,form2,…}] | 各 formi ごとに別々のリストを作る |
| Reap[expr,{form1,…},f] | 各タグと値のリストに f を適用する |
Wolframシステムの標準評価処理は，ユーザの式の入力を取り込み，式を評価し，評価が完了したら結果を返す，という過程からなっている．本節では，最終的な評価結果だけでなく，中間過程でも評価がどう進行するのかを見ていく．そうすることで，評価処理の理解の助けにもなるだろう．
Trace[expr]を使えば，式 expr の評価過程において中間結果として生成されるすべての中間式を列挙させることができる．ただし，もとの式が簡単なものでないと，非常に長いリストが出力されてしまい，Traceを行っても何のことか分からなくなってしまう．
Traceで指定するパターンは何でもよい．例えば，これでもよい：
例えば，関数facを作ったとして，その関数が呼び出されているときだけトレースを実行したければ，パターンをfac[n_]にしTraceに与えておく．また，パターンをf[n_,2]としておけば，引数を伴った特殊構成の関数式だけを抽出できるようになる．
Wolframシステムによる典型的なプログラムでは，fac[n]等の関数呼出しの式だけでなく，変数の割当てや，制御構造体等のいろいろな要素が登場する．これらの要素はすべて一般的な「式」とみなされるので，Traceに適切なパターン指定さえしておけば，どんな要素でも個別に抽出することができる．例えば，パターンをk=_としておけば，変数kに関するどんな割当て式でも抽出できるようになる．
式 expr の評価において，そのどの過程で生成された中間式でもTrace[expr,form]を使えば限定抽出することができる．また，抽出すべき中間式は式 expr から直接得られるものでなくてもよい．つまり，expr の評価処理の一部として関数が呼び出され，その結果生成されるような式であってもよい．
以上のように，Traceを使い中間式を追跡することができるが，追跡の対象になる式はユーザ定義の関数だけでなく，一部の組込み関数でもよい．ただし，注意点として組込み関数の場合，Wolframシステムのバージョンによってはアルゴリズムの記述や最適化処理が詳細な点で違うため，評価過程の順序が違ってくる場合がある．
| Trace[expr,f[___]] | 式の評価における関数 f の呼出しをすべて表示する |
| Trace[expr,i=_] | 変数 i への割当て式だけを表示する |
| Trace[expr,_=_] | すべての割当て式を表示する |
| Trace[expr,Message[___]] | 評価中に生成されるメッセージを表示する |
Traceの限定
関数Traceにより出力される式のリストは，Wolframシステムの計算処理の履歴である．中間式は計算処理で実行された順序通りに並べられる．また，Traceの結果のリストは，ほとんどの場合，ネストされた形で出力されるが，これは実際に行われた計算の「構造」を表している．
基本的に，Traceの結果であるリストの持つサブリストは，特定のWolframシステム式の評価チェーン（鎖）を表す．また，サブリストの要素はチェーンに相当し，1つの式が取るいろいろな変換形を表している．ただし，通常は，1つの式を評価するには他の式も評価しなければならないので，実際のTraceでは，従属評価の結果もサブリストに含まれることになる．
あるWolframシステム式の評価において従属評価を必要とする状況は基本的に2つある．1つは，式が複数の副次的な式からなる場合で，そのとき各副次式は別々に評価される必要がある．もう1つは，式の評価において規則が適用され，その適用時に別の関連式をも評価する必要がある場合である．どちらの場合も，従属評価の結果は，Traceにより返される構造体におけるサブリストとして表される．
再帰的処理を踏む関数の評価をトレースさせると，結果はネストされたリスト形で得られる．これは，評価の対象となる関数は1つでも，反復過程の途中で新たに生成される中間式が評価前の中間式に従属する形で生成されるからである．
式の評価過程で生成される中間式は，変換規則が適用された結果発生する．「異なるシンボルへの定義式の関連付け」で説明したように，定義済みの変換規則はすべて特定のシンボルに直接，もしくは，タグを介して間接的に関連付けられる．Trace[expr,f]を使い，式 expr をトレースさせることで，シンボル f に関連付けられている変換規則がどう適用されるかを調べることができる．この場合，Traceは，規則の適用前の中間式だけでなく，適用後の結果である中間式も返す．
Trace[expr,form]を使い式 expr をトレースさせると，パターン form にマッチした評価直前の中間式，または，そのパターンにマッチした，使われた規則に関連付けられたタグがすべて抽出される．
| Trace[expr,form,TraceOn->oform] | 中間式が oform にマッチした要素を持つときのステップだけをトレースする |
| Trace[expr,form,TraceOff->oform] | 中間式が oform にマッチした要素を持たないときのステップをトレースする |
Trace[expr,form]を使うと，パターン form に合った中間式だけが抽出されるが，トレース範囲としては，式 expr のすべての評価ステップが対象になる．場合によっては，expr の評価における範囲を限定して，限られたステップ中だけでトレースを行いたい．
これを行うには，TraceOn->oform のオプション設定を使う．パターン oform にマッチした要素を持つ中間式のステップに限ってトレースが実行される．反対に，あるステップだけをトレースから排除したければ，TraceOff->oform とすることで，oform を持つ中間式を除いたステップだけをトレースすることができる．
| Trace[expr,lhs->rhs] | 式 expr の評価において，左辺 lhs にマッチするすべての中間式を抽出し，右辺 rhs に変換し表示する |
Trace関数の強力な面として，この関数により返されるリストは，基本的に，他の関数で操作できる標準的なWolframシステム式である．ただし，Traceによりリストの中の式にはHoldFormがかけられているので，そのままでは入力としては使うことができない．また，注意点として，HoldFormは内部で有効にはなっているが，表示が標準出力表記だと，HoldFormの記述自体は表示に現れない．
トレースされた中間式にはHoldFormがかけられているため，そのままでは入力には使えない：
標準の出力表記だと，どのリスト要素がTraceの評価結果のものか，または，評価前の式なのかは分かりづらい：
複雑な計算では，Traceで得られるリストもまた複雑な構成になりがちである．Trace[expr,form]を使えば，パターン form に合った中間式だけをリストの要素として抽出することができる．しかし，どんなパターンを使おうが，最終的に得られるリストのネスト構造は変わらない．
TraceDepth->n のオプション設定をTraceの指定に加えると，トレース可能なネストレベルの上限はレベル n に設定される．そうすることで，長くなる解法において，細かい計算をスキップし，主要ステップだけを追うことができるため，トレースの効率を上げることができる．さらに，オプションTraceDepthとTraceOffを組み合せて使えば，追跡したいステップをさらに絞れるのでTrace作業をさらに速くすることができる．
| Trace[expr,form,TraceDepth->n] | 式 expr のトレースにおいて，ネストレベル n 以下の評価ステップを列挙する |
Trace[expr,form]を使えば，式 expr の評価で生成される中間式のうち form に合ったものだけを抽出することができる．ただし，この方法だと式だけが列挙され，式の評価から求まる値は通常出力されない．TraceForward->Trueのオプション指定をTraceに加えておけば，評価結果も見ることができる．
Trace[expr,form]で抽出されるほとんどの式は評価チェーンの中間ステップで生成される式である．TraceForward->Trueの指定をした場合は，評価チェーンの最終ステップで得られる式もTrace結果に入れられる．また，指定をTraceForward->Allとすると，form にマッチした式が評価された後に評価チェーンにおいて生成されるすべての式が抽出される．
TraceForwardを有効にしておくと，特定の形の式がどう評価されるかを追跡することができるようになる．場合によっては，式がこれからどうなるかより，どうしてこの式になったかを知りたい．そのときは，オプションTraceBackwardを有効にしておく．すると，TraceBackwardにより特定の式が生成される前に評価チェーンがどうだったかを観察することができるようになる．
TraceForwardとTraceBackwardを使い分けると，評価チェーンを昇り降りして評価を追跡することができる．場合によっては，特定の評価チェーンから派生する子チェーンまで追跡したい．これを行うには，TraceAboveを指定する．例えば，TraceAbove->Trueと設定しておけば，関連するすべての子チェーンの最初と最後における中間式がTraceに含まれるようになる．また，TraceAbove->Allとしておけば，子チェーンの全ステップにおける式をTraceすることができるようになる．
| Trace[expr,form,opts] | オプション設定に従って，式 expr の評価をトレースする |
| TraceForward->True | form を含む評価チェーンの最後の式をリストに加える |
| TraceForward->All | 評価チェーンにおいて form 登場以降の全ステップで生成される式をリストに加える |
| TraceBackward->True | form を含む評価チェーンにおいて最初の式をリストに加える |
| TraceBackward->All | 評価チェーンにおいて form 登場以前の全ステップで生成される式をリストに加える |
| TraceAbove->True | form を含む子チェーンに通じる全評価チェーンにおいて最初と最後の式をリストに加える |
| TraceAbove->All | form を含む子チェーンに通じる全評価チェーンにおいて全ステップの式をリストに加える |
Trace[expr,…]の基本動作は次の通りである．まず，式 expr の評価の過程で生じる中間式が抽出される．次に，中間式がパターンや設定条件に見合うものかが判断され，そうならば，リスト出力用に内部保持される．このとき，式の持つ関数の引数が評価された後にできた中間式だけがTraceによる抽出の対象になる．また，TraceOriginal->Trueの設定が有効なら，引数が評価される前の式の形もTraceの対象にされる．
Traceで得られるリストには，通常，非自明的な評価チェーンのステップで生成された式だけが出力される．つまり，評価後と評価前で同じ式が得られるような評価ステップは除外される．ただし，TraceOriginal->Trueの指定が有効なときはその限りでなく，Traceでは自明的かどうかにかかわらず評価過程の全ステップが出力される．
Traceが有効である場合，自明的な評価チェーンも含むすべての式がトレースさせる：
オプション
|
デフォルト値
| |
| TraceForward | False | form 以降の評価チェーンの式を表示するかどうかを指定 |
| TraceBackward | False | form 以前の評価チェーンの式を表示するかどうかを指定 |
| TraceAbove | False | form を含む子チェーンを生みだす評価チェーンを表示するかどうかを指定 |
| TraceOriginal | False | 頭部と引数の評価を実行する前の式を表示するかどうかを指定 |
Traceで使われる補足的なオプション
実行中のプログラムにTraceを使うとき，プログラム中の局所変数をどのように扱うか，という問題が起る．「モジュールの動作の仕方」で説明するように，Module等の構成体ではスコープを限定した局所変数が使えるようになっている．従って，プログラム中のもとのコードで変数xを呼んでも，こうして設けられた局所変数にはx$nnn の形式で参照名が付けられる．
そこで，form に現れるシンボル x が，expr の実行で発生する形式 x$nnn の名前を持つすべてのシンボルにデフォルトでマッチするように，Trace[expr,form]が設定される．つまり，Trace[expr,x=_]と入力すると，もとのプログラムにおいて変数が x の名前で参照されている限り，それが大域定義のものでも局所定義のものでもトレースの対象にされる．
| Trace[expr,form,MatchLocalNames->False] | |
参照名が form で始まる局所変数をトレースリストから除外する | |
場合によっては，名前を x とする大域変数だけをトレースの対象としたい．局所変数の記述名がxであってもそれは除外したい．そうするには，MatchLocalNames->Falseのオプション設定を加えておく．
関数Traceを使うと，まず，式の計算処理が完全に実行され，次に，計算処理の履歴を示す中間式のリストが表示される．特に，計算が長くなる場合は，計算処理の進行に並行した形で随時トレース結果を観測することができると便利である．関数TracePrintを使えばそれが可能になる．この関数は機能上Traceと同じだが，表示の仕方が違う．つまり，Traceのように抽出したすべての式を最後にリストで一括表示するのではなく，中間式が生成されるたびに式の表示を逐一行う．
TracePrintにより返される一連の式は，Traceが返すリスト要素の式と同じである．TracePrintの式の表示において，画面左側のインデント幅は式のネストレベルを示している（これは，Traceリストにおけるサブリストのレベルに相当する）．TracePrintの動作設定には，Traceの設定で使ったオプションTraceOn，TraceOff，TraceForwardを使うことができる．ただし，TracePrintは順次，式を出力していくので，TraceBackwardの指定は行うことができない．また，TraceOriginalの設定値は実効的に常にTrueとされる．
| Trace[expr,…] | 式 expr の評価をトレースし，抽出した中間式は評価終了時にリスト形式で一括表示する |
| TracePrint[expr,…] | 式 expr の評価をトレースし，抽出した中間式は評価中に逐次表示する |
| TraceDialog[expr,…] | 式 expr の評価をトレースし，指定した中間式が生成されるとダイアログを開始する |
| TraceScan[f,expr,…] |
TraceDialogを使うと，計算処理を途中で一旦停止させ，停止時の演算環境をもとにWolframシステムと対話ができるようになる．評価で一時的に使われる変数の現行値を調べたり，別の値に再設定したりすることができる．ただし，微妙な点で（特に，パターンやモジュール変数等に関連した点で），通常の割当てとは違うので注意が必要である．
TraceDialogのトレース中に一連の式が生成されると関数Dialogが呼び出される（Dialogの機能詳細に関しては「ダイアログ」を参照のこと）．Dialogを呼び出すということは，2次的な計算セッションを開始させるということで，Wolframシステムとの対話は別の入出力行が使われ進行する．
式 expr のトレースで抽出される中間式に任意な関数 f を適用したければ，TraceScan[f,expr,…]の書式を使う．実際に f の適用がある式にはHoldFormが適用され，評価されないよう式が保護される．
TraceScan[f,expr,…]では，中間式が評価される前に関数 f が適用される．ここで，TraceScan[f,expr,patt,fp]を使うと，評価の前には f が適用され，評価の後には fp が適用されるようになる．
Wolframシステム内部には「評価スタック」と呼ばれる現在評価中の式を記録しておく場所が用意されている．関数Stackを使うと，そのスタックの記録内容を参照できる．計算を一時停止させたとき等にStackを実行し計算の状態がどうなっているか調べることができる．
Stack[]は，呼び出されるときに進行中の評価に関連したタグを返す：
評価スタックは，特定の計算においてWolframシステムの現在位置に到達するまでに，どの関数がどの他の関数を呼び出したかを表示してくれるものととらえることができる．こうして表示される式の列は，オプションTraceAboveをTrueとしたときのTrace関数により返される一連のネストしたリストの第1要素に相当する．
通常の入出力セッションで直接Stackを使うことはあまりないだろう．通常は，計算を一時保留にしてからダイアログモードにまず入り，その後で二次的セッションからStackを実行する（ダイアログに関しては「ダイアログ」を参照のこと）．
最も単純なのは，評価スタックが評価中のすべての式を記録できるように設定されている場合である．しかし，場合によっては，網羅しない方がよいときもある．例えば，Print[Stack[]]が実行されると，Printが常にスタックの最後の関数になってしまうため不具合が生じる．
StackInhibitを使えば，そのようなことが起らないようにできる．書式StackInhibit[expr]を使うと，式 expr の評価はされるが，評価で発生する関数呼出しはスタックに登録されないようになる．
| StackInhibit[expr] | 式 expr は評価するが，スタックへの記録を禁止する |
| StackBegin[expr] | 式 expr を評価し，新規スタックを使う |
| StackComplete[expr] | 式 expr を評価し，評価チェーンで生成される中間式もスタックに記録する |
StackInhibitとStackBeginを使い評価プロセスのどの部分をスタックに記録するか指定できる．StackBegin[expr]は，式 expr が評価される前に新たなスタックを用意する．つまり，スタックには式 expr の評価で使われたもの以外は記録されない．StackBeginの前に使われた関数等は入らない．TraceDialog[expr,…]等のダイアログ用関数では，まずStackBeginが呼び出され，それから式 expr が評価される．このため，スタックを参照することで，式 expr がどのように評価されるかは知ることができるが，TraceDialog自体がどう呼ばれたかは分からない．
Stackは現在評価中の式だけを表示する．このため，最も最近の式の形が表示される．しかし，場合によっては，過去に取った式の形を見ることができると好都合である．これを行うには，StackCompleteを使う．
StackComplete[expr]を使うと，評価中の各式から派生した評価チェーンの逐一をスタックに記録することができる．この機能は，TraceにTraceAbove->TrueとTraceBackward->Allのオプション設定をしたときに得られる機能に相当する．
式の評価でWolfram言語の取る基本操作は，式に変化が見られなくなるまで別の変換規則を適用していくというものである．このため，x=x+1のような割当て式を入力すると，評価が永久に終らないことになりかねない．そこで，有限回のステップが過ぎると（再帰回数の上限は大域変数$RecursionLimitで決定される）Wolfram言語は自動的に処理を強制停止するようになっている．もちろん，ユーザは手動でいつでも停止させることができる．
わざと無限ループになる式を入力する．$RecursionLimitの回数以上の評価ステップが繰り返されると処理が停止してしまう：
評価自体は終っていないので，保留とされた結果が返される．特別にReleaseHoldを呼び出すことで，中断した評価を続行させることも可能である：
| $RecursionLimit | 評価スタックの深さの上限 |
| $IterationLimit | ループ等の評価チェーンにおける最大繰返し数 |
わざと循環する定義を作る．この場合，評価は$IterationLimitのループ上限で停止する：
大域変数$RecursionLimitと$IterationLimitは，2つの基本的な繰返し方法を制御し，無限の評価処理が起らないようにするためにある．$RecursionLimitは評価スタックの最大量を決定する．また，Traceのリスト出力におけるネストレベル上限にもこのパラメータが使われる．これに対して，$IterationLimitは1つの評価チェーンの許容する最大ステップ数を決定する．このパラメータは，Traceのリスト出力における単一サブリストの長さにも相当する．
$RecursionLimitと$IterationLimit自体のデフォルト値はよくある計算負荷と平均的なコンピュータシステムの能力に合わせて設定してある．ユーザが上限パラメータを他の整数値に変更するのは構わないが，（デフォルトの下限より大きく）無限大Infinityより小さい整数値を指定する．特殊なシステムを使っていない限り，$RecursionLimit=Infinityとは設定してはいけない（「メモリ管理」を参照のこと）．
今度は，複雑な式は何もできない．計算自体は$IterationLimitの上限で停止する：
注意点として，無限ループを行うとコンピュータのメモリが多量に消費されてしまう．反復処理の上限が$IterationLimitで決定されるような計算では，中間結果として生成される構造体が巨大になるというようなことはない．しかし，$RecursionLimitで上限が決まる計算では，そのようなことがあり得る．再帰的な処理で生成される構造体は$RecursionLimitの上限値に正比例して増大し，計算する式によっては，$RecursionLimitに指数関数的に比例して増えるものもある．
x=x+1のような式が循環してしまうことは明白である．しかし，再帰的関係が少し込み入ったものになると，いつ計算が終了するかを確実に判断することは難しい．これは，基本的な注意事項だが，変換規則を適用する前には，必ず式の右辺と左辺で記述内容が違っていることを確認する．そうすれば，少なくとも，同じ変換規則を同じ式に繰り返し適用してしまうような初歩的な間違いを防ぐことができる．
まぎらわしいのは，規則が/;の条件に依存する場合である（/;の条件は「パターン適用範囲の制限」を参照のこと）．その条件が大域変数を参照しているときはさらにまぎらわしくなってしまう．式が変化しなくなりさえすれば，Wolfram言語にとって評価は終了したことになる．しかし，他の式の評価で大域変数の値が変わってしまい，評価結果が狂ってしまう可能性がある．このような状況を防ぐには，まず，大域変数を/;の条件では使わないようにする．それでも疑わしい場合は，Update[s]の書式を使い強制的に s を参照している式をすべて更新させる．また，Update[]と入力すれば，すべての式を無差別に更新させることができる．
「計算処理の一時停止」でキーボード操作による計算処理の一時停止の仕方を説明した．
場合によっては，停止操作をプログラムの中から直接行いたい．中断関数Interrupt[]を使えばそれができる．中断を行うと，「計算処理の一時停止」にあるように多くのシステムではメニューが表示されるので，そこから次に取る操作を対話的に選択することができる．
| Interrupt[] | 計算を途中で一時中断し保留状態にする |
| Abort[] | 計算を途中で放棄する |
| CheckAbort[expr,failexpr] | 式 expr を評価し結果を返す．評価が放棄された場合は failexpr を返す |
| AbortProtect[expr] | 式 expr の評価が終了するまで放棄が実行されないようにする |
式の評価を放棄すると，その式に関するすべての評価結果は無効になり，戻り値としては$Abortedが得られる．
関数CheckAbortを使えば，放棄の操作を差し止めることができる．CheckAbort[expr,failexpr]の書式で関数を式 expr に適用しておくと，CheckAbortがあっても，実際に評価は放棄されず，代りに式 failexpr が出力される．ダイアログ用の関数Dialog等ではCheckAbortが使われ放棄関数による実際の放棄操作が行われないようになっている．
洗練されたプログラムを構築する際には，放棄されては困る部分が出てくる．ダイアログによる対話的な放棄操作と，関数Abortを使った放棄操作はともに禁止にしておきたい．そのようなときは，AbortProtectを必要な部分に作用させておく．すると，放棄操作が起っても評価は続行され，評価終了時に，どんな放棄操作があったかが報告される．
AbortProtectを適用した式でも，CheckAbortを式の中に入れておくと，放棄操作が自動検出され，式 failexpr が評価される．failexpr にAbort[]の記述がない限り，放棄操作は無効になる．
f[x_]:=x Sin[x]と定義したとする．右辺の式x Sin[x]は，xがどのような値をとっても適用可能な形で格納される．ユーザによりxの値が特定されると，値はx Sin[x]に代入され式の評価が行われる．特定されるxの値は何でもよい．数値でも，リストでも，代数式であってもよい．Wolfram言語の内部コードはすべてのオブジェクト型に対応するように作られている．
しかし，すべてのオブジェクトに対応しなければいけないため，処理時間は余計にかかる．そこで，xが例えば，機械精度の数値であることがあらかじめ分かっているなら，多くの処理ステップを踏む必要がなくなるため，潜在的に，x Sin[x]のような式をもっと速く評価することが可能になる．
式で参照される変数がすべて数（もしくは論理変数）とみなせるなら，関数Compileを使うことで式を高速なコードにコンパイルすることができる．Compile[{x1,x2,…},expr]を使うと，式 expr はコンパイルされ，「コンパイル済み関数」を得ることができる．式を評価させるには，コンパイルされた関数に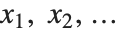 
を与えその関数を実行する．
を与えその関数を実行する． Compileの結果としてコンパイル済み関数CompiledFunctionと呼ばれるオブジェクトが生成される．そこには，実際のコンパイル済み関数の評価に必要な命令コード（インストラクション）が入っている．インストラクションは，使用されるコンピュータの機械語で書かれているので，高速な計算処理を実現することができる．
| Compile[{x1,x2,…},expr] | xi を数値的な変数とし，式 expr を計算するコンパイル済み関数を生成する |
x Sin[x]を評価してコンパイルした関数を作る：
数値を使う式や論理演算式を繰り返し評価する必要があるときは，Compileを使うと効率が上がる．関数Compileを一度呼び出すだけで，通常のWolfram言語関数に比べ高速に処理してくれるコードが手に入る．
x Sin[x]のように，式が単純であればコンパイルしようがしまいが処理速度はあまり違わない．しかし，式が長くなると，最大で20倍程度まで処理速度を上げることができるため，コンパイルするメリットが大きい．
コンパイルして著しい違いが出るのは，単純な（数論的な）関数をたくさん使った式の場合である．複雑な計算，例えば，ベッセル関数(BesselK)や固有値の解析関数(Eigenvalues)を使った計算では，コンパイルしても処理速度はあまり向上しない．これは，計算時間の大半が，コンパイル処理に影響されないWolfram言語内部のアルゴリズムで費やされるからである．
ルジャンドル(Legendre)多項式の10次項を求めるコンパイル済み関数を作る．EvaluateによってWolfram言語はコンパイルする前に多項式を明示的に構築する：
数値的な関数であればコンパイルすることで計算速度を上げられる．しかし，それでも，できるだけ組込み関数を使うようにした方がよい．組込み関数は最適化してあるので，コンパイルされたユーザ定義の関数より速いことが多い．それに，引数の型が何であろうと同一関数で処理することができる．コンパイル済み関数だと，特定精度の数値的な引数にしか対応することができない．
また，組込み関数によっては自らが関数Compileを呼び出してコンパイルを行うものがある．例えば，数値積分の関数NIntegrateは，与えられた積分式を自動的にCompileを使う．同じように，プロット関数PlotとPlot3Dはプロットする式をあらかじめCompileできるようになっている．Compileを利用する組込み関数にはコンパイル指定のオプションCompiledが用意されている．Compiled->Falseとしておけば，式のCompileを禁止にする．
| Compile[{{x1,t1},{x2,t2},…},expr] | 変数 xi を型 ti の数とみなし，式 expr をコンパイルする |
| Compile[{{x1,t1,n1},{x2,t2,n2},…},expr] | |
変数 xi を型 ti の数からなる ni 次元の配列とみなし，式 expr をコンパイルする | |
| Compile[vars,expr,{{p1,pt1},…}] | 式の要素 pi を型 pti のオブジェクトとみなし，式 expr をコンパイルする |
| _Integer | 機械精度の整数型 |
| _Real | 機械精度の近似実数型 |
| _Complex | 機械精度の近似複素数型 |
| TrueFalse | 論理変数 |
Compileの機能がうまく機能するには，式にある各オブジェクトの型が確定していることが不可欠である．特に指定がなければ，すべての変数は近似実数とみなされる．
別途指定さえすれば，変数が整数や複素数でも，真偽二値（TrueかFalse）の論理変数でも，さらに，数値配列的なものでもCompileをすることが可能である．変数の型を指定するにはパターンを使う．例えば，整数なら，_Integerとパターンを指定する．また，論理値の型なら，TrueかFalseでなければならない論理変数を指定するためにTrueFalseとパターンを指定する．
Compileの扱える変数の型は，基本的に，コンピュータが機械語レベルで直接処理できる型なら何でもよい．つまり，機械精度の近似実数はCompileが使える．しかし，任意桁精度の実数はコンパイルできない．さらに，整数に関しては，機械精度の整数，例えば，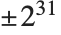
以内の整数にCompileを使うことができる．
以内の整数にCompileを使うことができる．コンパイルする式が四則演算や論理演算だけのものなら，Compileは入力される変数の型から演算の各ステップで生成される値はどの型のものか自動判定できる．しかし，他の関数を参照したりすると，Compileは返される値がどんな型のものか判断がつかなくなってしまう．そのようなときは，Compileは特に指定がなければ，戻り値はすべて近似実数の型とみなす．ただし，特別にリストで型のパターンを与えておけば，式を任意の型のものとして解釈させることも可能である．
Compileとは，引数の型に応じて最適化された関数を生成することにある．実は，Compileは，それが生成する関数がどんな型の引数を取ろうが正常に機能するようになっている．引数が最適化の対象以外の型なら，コンパイルした式ではなく，標準形の式が呼び出され，引数の型に応じた計算が行えるようになっている．
Compileが的確にコンパイルするためには，与える引数の型だけでなく，実行時に生じるオブジェクトすべてについて型が判明していなければならない．オブジェクトによっては，型が実行時の引数の型に依存し特定できない．例えば，Sqrt[x]として平方根を計算すると，x が正の値ならば，実数 x に対する平方根は実数になる．しかし，x が負の値のときは複素数になってしまう．
Compileは常に同じ型の値を返さなければいけない．もし，Compileにより生成されたコードを実行して，実際に返ってくる型が前提とした型と違うときは，このコードによる計算は無効にされ，代りに標準式による計算が行われる．
コンパイルするものが何であれ，コンパイル関数Compile[vars,expr]に与えた引数は評価されることなくコンパイル処理に直接回される．したがって，式の代りにプログラムもコンパイルすることができる．