GraphPlot3D

✖
`GraphPlot3D`

✖

GraphPlot3D[g]

generates a 3D plot of the graph g.

✖

GraphPlot3D[{e₁,e₂,…}]

generates a 3D plot of the graph with edges e_i.

✖

GraphPlot3D[{…,w[e_i],…}]

plots e_i with features defined by the symbolic wrapper w.

✖

GraphPlot3D[{v_{i 1}v_{j 1},…}]

uses rules v_ikv_jk to specify the graph g.

✖

GraphPlot3D[m]

uses the adjacency matrix m to specify the graph g.

Details and Options

GraphPlot3D attempts to place vertices in 3D to give a well-laid-out version of the graph.

GraphPlot3D supports the same vertices, edges and wrappers as Graph.
The following special wrappers can be used for the edges e_i:

	Annotation[e_i,label]	provide an annotation
	Button[e_i,action]	define an action to execute when the element is clicked
	EventHandler[e_i,…]	define a general event handler for the element
	Hyperlink[e_i,uri]	make the element act as a hyperlink
	Labeled[e_i,…]	display the element with labeling
	PopupWindow[e_i,cont]	attach a popup window to the element
	StatusArea[e_i,label]	display in the status area when the element is moused over
	Style[e_i,opts]	show the element using the specified styles
	Tooltip[e_i,label]	attach an arbitrary tooltip to the element

GraphPlot3D has the same options as Graphics3D, with the following additions and changes: [List of all options]

DataRange	Automatic	the range of vertex coordinates to generate
DirectedEdges	False	whether to interpret Rule as DirectedEdge
EdgeLabels	None	labels and placements for edges
EdgeLabelStyle	Automatic	style to use for edge labels
EdgeShapeFunction	Automatic	generate graphic shapes for edges
EdgeStyle	Automatic	styles for edges
GraphLayout	Automatic	how to lay out vertices and edges
GraphHighlight	{}	vertices and edges to highlight
GraphHighlightStyle	Automatic	style for highlight
Method	Automatic	method to use
PerformanceGoal	Automatic	aspects of performance to try to optimize
PlotStyle	Automatic	graphics directives to determine styles
PlotTheme	Automatic	overall theme for the graph
VertexCoordinates	Automatic	coordinates for vertices
VertexLabels	None	labels and placements for vertices
VertexLabelStyle	Automatic	style to use for vertex labels
VertexShape	Automatic	graphic shape for vertices
VertexShapeFunction	Automatic	generate graphic shapes for vertices
VertexSize	Automatic	size of vertices
VertexStyle	Automatic	styles for vertices

With the setting VertexCoordinates->Automatic, the embedding of vertices and routing of edges is computed automatically, based on the setting for GraphLayout.
Possible special embeddings for GraphLayout include:

		"BipartiteEmbedding"	vertices on two parallel lines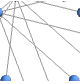
		"CircularEmbedding"	vertices on a circle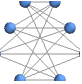
		"CircularMultipartiteEmbedding"	vertices on segments of a circle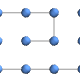
		"DiscreteSpiralEmbedding"	vertices on a discrete spiral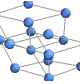
		"GridEmbedding"	vertices on a grid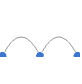
		"LinearEmbedding"	vertices on a line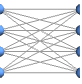
		"MultipartiteEmbedding"	vertices on several parallel lines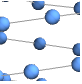
		"SpiralEmbedding"	vertices on a 3D spiral projected to 2D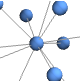
		"StarEmbedding"	vertices on a circle with a center

Possible structured embeddings for layered graphs such as trees and directed acyclic graphs include:

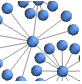
		"BalloonEmbedding"	vertices on a circle with the center at the parent vertex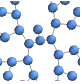
		"RadialEmbedding"	vertices on a circular segment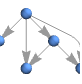
		"LayeredDigraphEmbedding"	vertices on parallel lines for directed acyclic graphs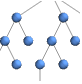
		"LayeredEmbedding"	vertices on parallel lines

Possible optimizing embeddings all minimize a quantity and include:

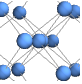
		"HighDimensionalEmbedding"	energy for spring-electrical in high dimension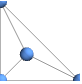
		"PlanarEmbedding"	number of edge crossings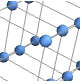
		"SpectralEmbedding"	weighted sum of squares distances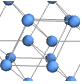
		"SpringElectricalEmbedding"	energy with edges as springs and vertices as charges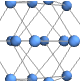
		"SpringEmbedding"	energy with edges as springs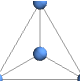
		"TutteEmbedding"	number of edge crossings and distance to neighbors

Possible settings for PlotTheme include common base themes, color feature themes, font features themes, and size features themes.

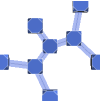
		"Business"	a bright, modern look appropriate for business presentations or infographics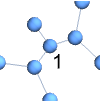
		"Detailed"	identify data by employing labels and tooltips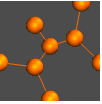
		"Marketing"	elegant, eye-catching design suitable for marketing needs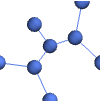
		"Minimal"	simple graph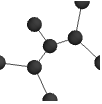
		"Monochrome"	single-color design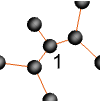
		"Scientific"	candid design useful for analyzing detailed data with labels and tooltips
		"Web"	clean, bold design suitable for a consumer website or blog
		"Classic"	historical design of graph to remain compatible with existing uses

Graph features themes affect plot of vertices and edges. Feature themes include:
"LargeGraph" large graph

"ClassicLabeled" classic graph

"IndexLabeled" index-labeled graph

List of all options

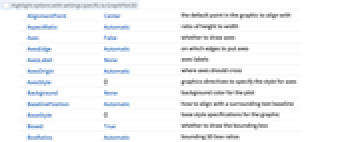
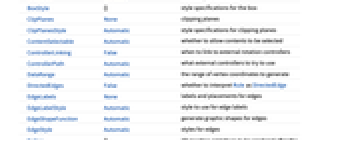
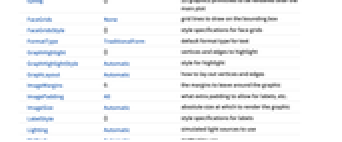
AlignmentPoint	Center	the default point in the graphic to align with
AspectRatio	Automatic	ratio of height to width
Axes	False	whether to draw axes
AxesEdge	Automatic	on which edges to put axes
AxesLabel	None	axes labels
AxesOrigin	Automatic	where axes should cross
AxesStyle	{}	graphics directives to specify the style for axes
Background	None	background color for the plot
BaselinePosition	Automatic	how to align with a surrounding text baseline
BaseStyle	{}	base style specifications for the graphic
Boxed	True	whether to draw the bounding box
BoxRatios	Automatic	bounding 3D box ratios
BoxStyle	{}	style specifications for the box
ClipPlanes	None	clipping planes
ClipPlanesStyle	Automatic	style specifications for clipping planes
ContentSelectable	Automatic	whether to allow contents to be selected
ControllerLinking	False	when to link to external rotation controllers
ControllerPath	Automatic	what external controllers to try to use
DataRange	Automatic	the range of vertex coordinates to generate
DirectedEdges	False	whether to interpret Rule as DirectedEdge
EdgeLabels	None	labels and placements for edges
EdgeLabelStyle	Automatic	style to use for edge labels
EdgeShapeFunction	Automatic	generate graphic shapes for edges
EdgeStyle	Automatic	styles for edges
Epilog	{}	2D graphics primitives to be rendered after the main plot
FaceGrids	None	grid lines to draw on the bounding box
FaceGridsStyle	{}	style specifications for face grids
FormatType	TraditionalForm	default format type for text
GraphHighlight	{}	vertices and edges to highlight
GraphHighlightStyle	Automatic	style for highlight
GraphLayout	Automatic	how to lay out vertices and edges
ImageMargins	0.	the margins to leave around the graphic
ImagePadding	All	what extra padding to allow for labels, etc.
ImageSize	Automatic	absolute size at which to render the graphic
LabelStyle	{}	style specifications for labels
Lighting	Automatic	simulated light sources to use
Method	Automatic	method to use
PerformanceGoal	Automatic	aspects of performance to try to optimize
PlotLabel	None	a label for the plot
PlotRange	All	range of values to include
PlotRangePadding	Automatic	how much to pad the range of values
PlotRegion	Automatic	final display region to be filled
PlotStyle	Automatic	graphics directives to determine styles
PlotTheme	Automatic	overall theme for the graph
PreserveImageOptions	Automatic	whether to preserve image options when displaying new versions of the same graphic
Prolog	{}	2D graphics primitives to be rendered before the main plot
RotationAction	"Fit"	how to render after interactive rotation
SphericalRegion	Automatic	whether to make the circumscribing sphere fit in the final display area
Ticks	Automatic	specification for ticks
TicksStyle	{}	style specification for ticks
TouchscreenAutoZoom	False	whether to zoom to fullscreen when activated on a touchscreen
VertexCoordinates	Automatic	coordinates for vertices
VertexLabels	None	labels and placements for vertices
VertexLabelStyle	Automatic	style to use for vertex labels
VertexShape	Automatic	graphic shape for vertices
VertexShapeFunction	Automatic	generate graphic shapes for vertices
VertexSize	Automatic	size of vertices
VertexStyle	Automatic	styles for vertices
ViewAngle	Automatic	angle of the field of view
ViewCenter	Automatic	point to display at the center
ViewMatrix	Automatic	explicit transformation matrix
ViewPoint	{1.3,-2.4,2.}	viewing position
ViewProjection	Automatic	projection method for rendering objects distant from the viewer
ViewRange	All	range of viewing distances to include
ViewVector	Automatic	position and direction of a simulated camera
ViewVertical	{0,0,1}	direction to make vertical

Examples

open allclose all

Basic Examples (3)Summary of the most common use cases

Plot a graph in 3D:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-44zizu

Out[1]=1

Plot a graph specified by edge rules:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-n7upo2

Out[1]=1

Plot a graph specified by its adjacency matrix:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-eor

Out[1]=1

Scope (12)Survey of the scope of standard use cases

Graph Specification (6)

Specify a graph using a graph:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-6n4s8z

Out[1]=1

Specify a graph using a rule list:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-jiad

Out[1]=1

Specify a graph using a dense adjacency matrix:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-es74ar

Out[1]=1

Specify a graph using a sparse adjacency matrix:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-xxsr21

Out[1]=1

Use GraphData for collections of graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-bym1l

Out[1]=1

Use ExampleData for collections of sparse matrices:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-9jq5p1

Out[1]=1

Graph Styling (6)

Give labels for some edges:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-dzwc2j

Out[1]=1

Give vertex labels:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-lyhsxv

Out[1]=1

Show edges as arrows:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-rnd2yf

Out[1]=1

Plot a disconnected graph using different packing methods:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-fhg2mx

Out[1]=1

For very large graphs, it is often better not to draw vertices at all:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-vp04ih

Out[1]=1

Use EdgeShapeFunction and VertexShapeFunction for detailed control:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-payab

Out[1]=1

Options (71)Common values & functionality for each option

DataRange (1)

Specify the range of vertex coordinates:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-1w5kej

Out[1]=1

DirectedEdges (1)

Show the direction of edges:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-4wjzw0

Out[1]=1

GraphLayout (66)

"BalloonEmbedding" (6)

Place each vertex in an enclosing circle centered at its parent vertex:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-nbz2f7

Out[1]=1

"BalloonEmbedding" works best for tree graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-8ufl0n

Out[1]=1

Use the option "EvenAngle"->True to place vertices evenly in an enclosing circle:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-kwbqgo

Out[1]=1

With the setting "OptimalOrder"->True, the vertex ordering optimizes the angular resolution and the aspect ratio:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-uvg4ev

Out[1]=1

Use the option "RootVertex"->v to set the root vertex:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-1eeop6

Out[1]=1

Use "SectorAngles"->s to control the size of each sector:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-ojpa37

Out[1]=1

"BipartiteEmbedding" (1)

Place vertices on two vertical lines based on a bipartite partition:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-z5s32c

Out[1]=1

"CircularEmbedding" (2)

Place vertices on a circle:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-7r1e5

Out[1]=1

Use the option "Offset"->offset to specify the offset angles:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-e5r0wp

Out[1]=1

"CircularMultipartiteEmbedding" (2)

Place vertices on polygon lines based on a vertex partition:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-toa8ih

Out[1]=1

Use "VertexPartition"->partition to specify a partition of vertices:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-bmew69

Out[1]=1

"DiscreteSpiralEmbedding" (3)

Place vertices on a discrete spiral:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-ociz1f

Out[1]=1

"DiscreteSpiralEmbedding" works best for path graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-erfyib

Out[1]=1

With the setting "OptimalOrder"True, vertices are reordered so that they lie nicely on a discrete spiral:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-7zxrnm

Out[1]=1

"GridEmbedding" (2)

Place vertices on a grid:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-q2ovv5

Out[1]=1

Use "Dimension"->dim to specify a dimension of a grid:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-e1miro

Out[1]=1

"HighDimensionalEmbedding" (2)

Place vertices in high dimension according to spring-electrical embedding and project down:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-xl28fv

Out[1]=1

Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-xa2mwc

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-xlfz2e

Out[2]=2

"LayeredEmbedding" (6)

Place vertices in several layers in such a way as to minimize edges between nonadjacent layers:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-jz9m2n

Out[1]=1

"LayeredEmbedding" works best for tree graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-s85lds

Out[1]=1

Use the option "LayerSizeFunction"->func to specify the relative height:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-c5i4rh

Out[1]=1

Use the option "RootVertex"->v to set the root vertex:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-1e4g1s

Out[1]=1

Use the option "LeafDistance"->d to specify the leaf distance:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-v5dp5p

Out[1]=1

Use the option "Orientation"->o to draw a tree with different orientations:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-uuxtyo

Out[1]=1

"LayeredDigraphEmbedding" (3)

Place vertices in a series of layers:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-nkj7be

Out[1]=1

Use the option "RootVertex"->v to set the root vertex:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-6f04i

Out[1]=1

Use the option "Orientation"->o to draw a tree with different orientations:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-c76mto

Out[1]=1

"LinearEmbedding" (2)

Place vertices on a line:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-8pwjrw

Out[1]=1

Use the option "Method"->m to specify the algorithm:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-ioh8ie

Out[1]=1

"MultipartiteEmbedding" (2)

Place vertices on multiple line grids based on a vertex partition:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-74b75y

Out[1]=1

Use "VertexPartition"->partition to specify a partition of vertices:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-41v6mz

Out[1]=1

"PlanarEmbedding" (1)

Place vertices on a plane without an edge crossing:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-uttueq

Out[1]=1

"RadialEmbedding" (2)

Place vertices in concentric circles:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-l9pix6

Out[1]=1

Use the option "RootVertex"->v to set the root vertex:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-nu3wvt

Out[1]=1

"RandomEmbedding" (1)

Place vertices randomly:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-jk4qr7

Out[1]=1

"SpectralEmbedding" (2)

Place vertices so the weighted sum of squares of mutual distances is minimized:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-07urxv

Out[1]=1

Use the option "RelaxationFactor"->r to get the layout based on a relaxed Laplace matrix.

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-2pn79u

Out[1]=1

"SpiralEmbedding" (2)

Place vertices on a spiral:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-gavq9g

Out[1]=1

With the setting "OptimalOrder"->True, vertices are reordered so that they lie on the spiral nicely:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-otgemm

Out[1]=1

"SpringElectricalEmbedding" (12)

Place vertices so that they minimize mechanical and electrical energy when each vertex has a charge and each edge corresponds to a spring:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-66vox6

Out[1]=1

With the setting "EdgeWeighted"->True, edge weights are used:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-pcwxis

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-ycr55

Out[2]=2

Use the option "EnergyControl"->e to specify limitations on the total energy of the system during minimization:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-frmrff

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-5gf4l0

Out[2]=2

Use "InferentialDistance"->d to specify a cutoff distance beyond which the interaction between vertices is assumed to be nonexistent:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-7y6k6p

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-rsd5kl

Out[2]=2

Use "MaxIteration"->it to specify a maximum number of iterations to be used in attempting to minimize the energy:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-zt30w6

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-ny81th

Out[2]=2

Use "Multilevel"->method to specify a method used during a recursive procedure of coarsening a graph:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-bkryd8

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-e3ocs3

Out[2]=2

With the setting "Octree"->True, an octree data structure (in three dimensions) or a quadtree data structure (in two dimensions) is used in the calculation of repulsive force:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-2s8917

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-4hsej8

Out[2]=2

Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-pienrf

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-h1779y

Out[2]=2

Use "RepulsiveForcePower"->r to control how fast the repulsive force decays over distance:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-cne41e

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-em0025

Out[2]=2

Use "StepControl"->method to define how step length is modified during energy minimization:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-lsbsuc

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-zcbotu

Out[2]=2

Use "StepLength"->r to specify the initial step length used in moving the vertices around:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-ov5k0g

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-zftq5g

Out[2]=2

Use "Tolerance"->r to specify the tolerance used in terminating the energy minimization process:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-rltxny

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-yw9m8a

Out[2]=2

"SpringEmbedding" (10)

Place vertices so that they minimize mechanical energy when each edge corresponds to a spring:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-s5baes

Out[1]=1

With the setting "EdgeWeighted"->True, edge weights are used:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-x4uvqp

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-gs5vmp

Out[2]=2

Use the option "EnergyControl"->e to specify limitations on the total energy of the system during minimization:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-ih0fzt

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-oza266

Out[2]=2

Use "InferentialDistance"->d to specify a cutoff distance beyond which the interaction between vertices is assumed to be nonexistent:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-pgxo89

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-5k3wpc

Out[2]=2

Use "MaxIteration"->it to specify a maximum number of iterations to be used in attempting to minimize the energy:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-3ya7yg

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-sms8wz

Out[2]=2

Use "Multilevel"->method to specify a method used during a recursive procedure of coarsening a graph:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-zmy9dc

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-wls559

Out[2]=2

Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-1dvu0n

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-th0tg9

Out[2]=2

Use "StepControl"->method to define how step length is modified during energy minimization:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-desuuz

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-b7tb38

Out[2]=2

Use "StepLength"->r to specify the initial step length used in moving the vertices around:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-ub618a

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-z2cb07

Out[2]=2

Use "Tolerance"->r to specify the tolerance used in terminating the energy minimization process:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-gvtgsl

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-pu79d1

Out[2]=2

"StarEmbedding" (3)

Place vertices on a star shape:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-je2zlx

Out[1]=1

Use the option "Offset"->offset to specify the offset angles:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-p7zdm2

Out[1]=1

Use the option "Center"->center to specify the center:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-7suw46

Out[1]=1

"TutteEmbedding" (2)

Place vertices without crossing edges and minimize the sum of distances to neighbors:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-iufsxc

Out[1]=1

"TutteEmbedding" works for 3-connected planar graphs only:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-1ilav6

Out[1]=1

PlotStyle (3)

Specify an overall style for the graph:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-iyhlr

Out[1]=1

PlotStyle can be combined with VertexShapeFunction, which has higher priority:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-qwf78x

Out[1]=1

PlotStyle can be combined with EdgeShapeFunction, which has higher priority:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-d77bnc

Out[1]=1

Applications (2)Sample problems that can be solved with this function

Make a 3D graph layout with spheres and cylinders:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-do02fl

Out[1]=1

Structure an engineering matrix:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-ygpqom

Out[1]=1

Properties & Relations (7)Properties of the function, and connections to other functions

Use LayeredGraphPlot for hierarchical-style drawing of directed graphs:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-82938a

Out[1]=1

Use TreePlot for different types of tree drawing:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-j673mq

Out[1]=1

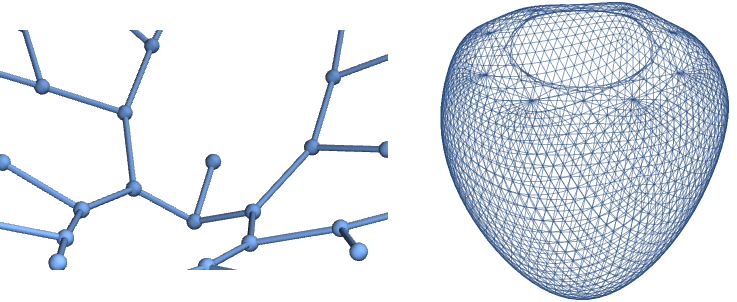
Use GraphPlot to draw graphs in 2D:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-fpwld

Out[1]=1

Use GraphData for an extensive collection of predefined graphs and properties:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-fqfxu2

Get the connectivity and plot it:

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-l9vdut

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0rs6prk6g-bnocv

Out[3]=3

Use PolyhedronData for a large collection of polyhedra and properties:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-fj0n2c

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-irjd4t

Out[2]=2

Compare to a predefined embedding:

In[3]:=3

✖

https://wolfram.com/xid/0rs6prk6g-hiue1k

Out[3]=3

Use ExampleData for a large collection of sparse matrices:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-zf0av1

Out[1]=1

Use ArrayPlot or MatrixPlot to display sparse matrices:

In[1]:=1

✖

https://wolfram.com/xid/0rs6prk6g-u08exi

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0rs6prk6g-s0w9v2

Out[2]=2

Top

		"LargeGraph"	large graph
		"ClassicLabeled"	classic graph
		"IndexLabeled"	index-labeled graph

GraphPlot3D ✖ GraphPlot3D

Details and Options

List of all options

Examples

Basic Examples (3)Summary of the most common use cases

Scope (12)Survey of the scope of standard use cases

Graph Specification (6)

Graph Styling (6)

Options (71)Common values & functionality for each option

DataRange (1)

DirectedEdges (1)

GraphLayout (66)

"BalloonEmbedding" (6)

"BipartiteEmbedding" (1)

"CircularEmbedding" (2)

"CircularMultipartiteEmbedding" (2)

"DiscreteSpiralEmbedding" (3)

"GridEmbedding" (2)

"HighDimensionalEmbedding" (2)

"LayeredEmbedding" (6)

"LayeredDigraphEmbedding" (3)

"LinearEmbedding" (2)

"MultipartiteEmbedding" (2)

"PlanarEmbedding" (1)

"RadialEmbedding" (2)

"RandomEmbedding" (1)

"SpectralEmbedding" (2)

"SpiralEmbedding" (2)

"SpringElectricalEmbedding" (12)

"SpringEmbedding" (10)

"StarEmbedding" (3)

"TutteEmbedding" (2)

PlotStyle (3)

Applications (2)Sample problems that can be solved with this function

Properties & Relations (7)Properties of the function, and connections to other functions

See Also

Related Guides

History

Text

CMS

APA

BibTeX

BibLaTeX

GraphPlot3D

✖
`GraphPlot3D`