





Integrate 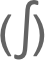
詳細とオプション


- Integrate[f,x]は ∫fx として入力できる.
- ∫ は,
 int
int または\[Integral]として入力できる.
または\[Integral]として入力できる. - は通常のdと異なり,
 dd
dd または\[DifferentialD]として入力される.
または\[DifferentialD]として入力される. - Integrate[f,{x,y,…}∈reg]は ∫{x,y,…}∈regf として入力できる.
- Integrate[f,{x,xmin,xmax}]は,xminを ∫の下付き文字として,xmaxを上付き文字として表すことによって入力できる.
- 多重積分は,標準的な反復表記の変形を使用する.第1変数は,最も外側の積分に対応して与えられ,これが最後に実行される. »
- Integrateは,有理関数の積分を評価することができる.また,結果が同じ関数の組で表すことができる範囲で指数関数,対数関数,三角関数,そして逆三角関数の積分を評価することができる.
- Integrateは,多くの特別関数によって結果を与えることができる.
- Integrateは,明示的に積分できないものについてはある種の簡約化を実行する.
- 定積分については,Nを適用することで数値的な結果を得ることができる. »
- 新しいクラスの積分に結果を与えるために,Integrateが関わるパターンに値を割り当てることができる.
- 積分変数は x[i]のような構造や,頭部が数学関数ではない任意の式でもよい.
- 不定積分において,Integrateは,ほとんどすべてのパラメータの値に対して正しい結果を求める.
- 定積分において指定可能なオプション
-
Assumptions $Assumptions パラメータについての仮定を指定 GenerateConditions Automatic パラメータについての制約条件を含む解を生成するかどうか GeneratedParameters None 生成されたパラメータにどのように名前を付けるか PrincipalValue False コーシー主値を求めるかどうか - Integrateは,標準的な公式集に載っているすべての不定積分とほとんどの定積分が評価できる.
- StandardFormでは,Integrate[f,x]は ∫fx として出力される.
例題
すべて開く すべて閉じるスコープ (78)
基本的な用法 (13)
![]() intt
intt![]() を使ってテンプレート
を使ってテンプレート ![]() を入力し,
を入力し,![]() を使ってフィールド間を移動する:
を使ってフィールド間を移動する:
![]() dintt
dintt![]() を使ってテンプレート
を使ってテンプレート ![]() を入力し,
を入力し,![]() を使ってフィールド間を移動する:
を使ってフィールド間を移動する:
StandardFormでは,y が x の前に置かれる:
記号 ∈ は ![]() el
el![]() または ∈ と入力する:
または ∈ と入力する:
![]() rintt
rintt![]() を使ってテンプレート
を使ってテンプレート![]() を入力し,
を入力し,![]() を使ってフィールド間を移動する:
を使ってフィールド間を移動する:
記号積分に失敗すると,NIntegrateが自動的に呼び出される:
不定積分 (10)
これらはRootオブジェクトの和を含むことがある:
Integrateは,該当する場合は,複素平面上で有効な不定積分を返す:
Erfのような特殊関数についてのみ実行できる積分が多数ある:
PolyLogやLogIntegralのようなLogの一般化:
Hypergeometric2F1のような超幾何関数:
定積分 (13)
区分関数と一般化された関数の積分 (12)
Piecewise関数の不定積分を計算する:
不連続Piecewise関数を積分する:
定義されているすべての場所で,maxIntの導関数はもとの関数と等しくなる:
Piecewise関数の定積分を計算する:
Floorのような区分関数の定積分を計算する:
Assumptionsを使って有限数の場合で積分する:
ネストした積分 (12)
2つの変数についてのネストした積分についての2つの積分関数を生成する:
負の体積(薄い青)と正の体積(濃い灰色)が同じくらいである:
CoordinateChartDataで超球面座標の座標範囲を見る:
領域積分 (11)
同様に,Booleを使って長方形領域上で円板に限定して積分する:
Booleを使って表現された同じ積分:
GenerateConditions Trueのとき,領域が退化しないように仮定が生成される:
ImplicitRegionとして領域を定義し,この領域上で直接積分する:
RegionPlot3Dを使って3D領域を可視化する:
積分の記号的な特徴 (7)
積分のLaplaceTransformを計算する:
オプション (11)
Assumptions (3)
デフォルトで,収束を確かなものとするパラメータについての条件が生成される:
Assumptionsを使うと,与えられた仮定の下で有効な結果が返される:
Assumptionsを手動で指定して,自動的に生成された条件外の値を確かめる:
GenerateConditions (2)
GeneratedParameters (4)
GeneratedParametersの値を指定して一般的な不定積分を得る:
入力式にすでに生成されたパラメータが含まれている場合は,使用可能な次の指標が使われる:
複数の変数を持つネストした積分の場合は,不定積分が任意の関数を含む:
GeneratedParametersの値が生成された各パラメータの指標に適用される:
Noneという値は生成されたパラメータを無効にする:
アプリケーション (67)
積分の幾何学 (5)
定数関数 ![]() の積分
の積分 ![]() は,高さ
は,高さ ![]() ,幅
,幅 ![]() の長方形の符号付き面積である:
の長方形の符号付き面積である:
区分定数関数の積分 ![]() はそのプロットで定義される長方形の符号付き面積の和である:
はそのプロットで定義される長方形の符号付き面積の和である:
一般的な関数の積分 ![]() は,そのプロットと水平軸の間の符号付き面積である:
は,そのプロットと水平軸の間の符号付き面積である:
これは,そのプロットで定義された長方形について考えると,区分定数の場合と関連している:
区間[0,2]上の n5についての長方形は以下のようになる:
これらの長方形の面積は,曲線の下の面積を近似するリーマン和を定義する:
DiscreteLimitを使って,Integrateと同じように,![]() のときに厳密な答を得る:
のときに厳密な答を得る:
微積分の基本定理は,関数を固定下限から可変上限までの積分に関連付ける:
![]() は,
は,![]() についての次の表で説明されているように,高さ
についての次の表で説明されているように,高さ ![]() で幅
で幅 ![]() の長方形と
の長方形と ![]() で消えてしまう小さい修正からなる面積であることに注意のこと:
で消えてしまう小さい修正からなる面積であることに注意のこと:
したがって,極限は,次の可視化で説明されるように,幾何学的に ![]() に等しいものと見ることができる:
に等しいものと見ることができる:
Interpolationでデータの離散集合を積分する:
曲線間の面積 (7)
回転領域 (7)
弧長,曲面の面積,および体積 (8)
線積分 (6)
原点を中心とした半長軸が![]() と
と![]() の楕円上で
の楕円上で ![]() の線形積分
の線形積分 ![]() を計算する:
を計算する:
以下のパラメータ化された曲線上で ![]() の閉じた線形積分
の閉じた線形積分 ![]() を計算する:
を計算する:
この曲線は,以下のプロットで示されているように,赤から紫に進む無限大の形を形成する:
頂点![]() ,
,![]() ,
,![]() の三角形上で ∫x4dx+x yyを計算するために,関連するベクトル場を定義する:
の三角形上で ∫x4dx+x yyを計算するために,関連するベクトル場を定義する:
粒子が![]() (
(![]() )から
)から![]() (
(![]() )までの以下のパスを通るときの,力
)までの以下のパスを通るときの,力 ![]() によってなされた仕事を計算する:
によってなされた仕事を計算する:
時点![]() における原点から時点
における原点から時点![]() における
における![]() まで進む,直線を通る曲線の族を定義する:
まで進む,直線を通る曲線の族を定義する:
Gradを使って ![]() が
が ![]() のポテンシャル関数であることを確認する:
のポテンシャル関数であることを確認する:
グリーンの定理(Green's Theorem) を使って次の曲線で囲まれた部分の面積を求める:
次のベクトル場は![]() の二次元Curlを持つ:
の二次元Curlを持つ:
曲面と体積の積分 (7)
グリーンの定理を使って,原点を中心として半径3の円の上で ![]() を計算する:
を計算する:
ベクトル場の循環はCurlを使って行うことができる:
Stokeの定理 ![]() には,境界上の
には,境界上の ![]() の線形積分は曲面を通るその回転の流束積分に等しいとある:
の線形積分は曲面を通るその回転の流束積分に等しいとある:
発散定理を使って,上界が ![]() .下界が
.下界が ![]() で両側の境界が
で両側の境界が ![]() と
と ![]() である曲面を通る
である曲面を通る ![]() の流束を計算する:
の流束を計算する:
ガウス定理を使って以下のパラメトリック曲面で包み込まれた部分の体積を求める:
質量密度 ![]() が与えられた場合に,以下で与えられる領域の質量を求める:
が与えられた場合に,以下で与えられる領域の質量を求める:
平均値と重心 (6)
![]() から
から![]() までの曲線
までの曲線 ![]() の下の領域の重心を計算するために,まず 面積を求める:
の下の領域の重心を計算するために,まず 面積を求める:
RegionCentroidが与える答と比較する:
RegionCentroidが返す答と比較する:
曲線 ![]() の下の
の下の ![]() から
から ![]() までの領域の重心の一般式を,積分は曲線の下の面積を与えるという事実を使って導出する:
までの領域の重心の一般式を,積分は曲線の下の面積を与えるという事実を使って導出する:
確率,期待値,標準偏差 (7)
Probabilityが返す値と比較する:
平均![]() の指数分布について
の指数分布について ![]() の確率を計算する.平均はパラメータの逆数である:
の確率を計算する.平均はパラメータの逆数である:
したがって,ExponentialDistribution[5/2]の確率密度関数(PDF)を使用する:
PDFは ![]() の場合に消失するため,
の場合に消失するため,![]() である確率は,
である確率は,![]() から
から![]() までの積分で与えられる:
までの積分で与えられる:
Probabilityが返す答と比較する:
これは,曲線の下の面積全体の![]() が,以下のプロットで
が,以下のプロットで ![]() と
と ![]() の間にあると解釈できる:
の間にあると解釈できる:
Expectationが返す答と比較する:
平均の μ 指数分布の標準偏差はやはり μ であることを示す:
MeanとStandardDeviationが返す答と比較する:
積分変換 (7)
FourierTransformと比較する:
LaplaceTransformと比較する:
この関数は偶関数なので,Hartley変換はFourierCosTransformに等しい:
MellinTransformと比較する:
HankelTransformと比較する:
実部と虚部の解析 (4)
ノルムは常に最終的に ![]() の増加関数であるが,はじめは減少するかもしれない:
の増加関数であるが,はじめは減少するかもしれない:
フーリエ変換は ![]() 同型(関数のノルムと変換したもののノルムは等しい)である:
同型(関数のノルムと変換したもののノルムは等しい)である:
![]() で定義された関数について,重み
で定義された関数について,重み ![]() で
で ![]() の重み付き内積を定義する:
の重み付き内積を定義する:
Integrateを使って関数の内積を定義する:
Orthogonalizeを使って正規直交基底を構築する:
内積はゲーゲンバウアー(Gegenbauer)多項式を生成する:
![]() における
における ![]() の剰余を,
の剰余を,![]() を包み込む輪郭線上での積分として計算する:
を包み込む輪郭線上での積分として計算する:
Residueが返す答と比較する:
特性と関係 (14)
定積分はDiscreteLimitとSumによって定義できる:
Nを使って積分を数値的に評価する:
これは,事実上,NIntegrateを呼び出す:
負の整数次数を持つDerivativeは積分を行う:
ArcLengthは,一次元領域上での1の積分である:
Areaは,二次元領域上での1の積分である:
Volumeは,三次元領域上での1の積分である:
領域 ![]() についてのRegionMeasureは積分
についてのRegionMeasureは積分 ![]() で与えられる:
で与えられる:
RegionCentroidは,m=RegionMeasure[ℛ]のIntegrate[p,p∈ℛ]/m に等しい:
DSolveValueは積分定数を持つ解を返す:
DSolveは解の置換規則を返す:
Integrateは積分を閉形式で計算する:
AsymptoticIntegrateは厳密解を近似する級数を与える:
FourierTransformは積分によって定義される:
LaplaceTransformは積分によって定義される:
考えられる問題 (12)
不定積分 (6)
単純な積分の中にも標準的な数学関数で評価できないものがたくさんある:
定積分を可変上界で使うと不連続なところが滑らかになる.プロットの左側の不連続点を求める:
この場合,前の不連続点から積分することにより,不定積分の値が![]() の範囲で再現される:
の範囲で再現される:
Simplifyおよび関連構造はしばしば同値を示す:
同じ被積分関数でも形式が異なると積分定数が異なる積分を与えることがある:
![]() のようなパラメータは不定積分の内側では汎用的であると仮定される:
のようなパラメータは不定積分の内側では汎用的であると仮定される:
定積分 (6)
不定積分の結果に上界下界を代入することでは定積分の正しい答が得られないかもしれない:
整数による仮定を指定してもより簡単な結果が与えられるとは限らない:
Simplifyおよび関連関数を使って望んだ結果を得る:
領域上の積分は,被積分関数が絶対に積分可能かどうかを調べはしない:
全空間の測度を使う場合は,条件![]() を加えて空間全体の上で積分する:
を加えて空間全体の上で積分する:
GenerateConditionsをFalseに設定すると予想しない答が返されるかもしれない:
インタラクティブな例題 (1)
関連項目
NIntegrate AsymptoticIntegrate LineIntegrate SurfaceIntegrate ContourIntegrate Asymptotic DSolve Sum LaplaceTransform FourierTransform Convolve D Derivative CDF Expectation Probability ArcLength Area Volume MomentOfInertia FractionalD CaputoD ResidueSum
文字: \[Integral] \[DifferentialD]
Function Repository: FractionalIntegrate RiemannSum
履歴
1988 で導入 (1.0) | 1996 で更新 (3.0) ▪ 2003 (5.0) ▪ 2014 (10.0) ▪ 2019 (12.0)
テキスト
Wolfram Research (1988), Integrate, Wolfram言語関数, https://reference.wolfram.com/language/ref/Integrate.html (2019年に更新).
CMS
Wolfram Language. 1988. "Integrate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Integrate.html.
APA
Wolfram Language. (1988). Integrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Integrate.html
BibTeX
@misc{reference.wolfram_2025_integrate, author="Wolfram Research", title="{Integrate}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Integrate.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_integrate, organization={Wolfram Research}, title={Integrate}, year={2019}, url={https://reference.wolfram.com/language/ref/Integrate.html}, note=[Accessed: 17-February-2026]}