グラフィックスとサウンドオブジェクトの構造
「グラフィックスとサウンド」において,PlotとListPlot等のプロット関数の使い方を説明した.ここでは,プロット関数で生成したグラフィックスがWolfram言語内部でどのような形式で保管されているか,また,より複雑なグラフィックスを作成するにはWolfram言語をどのようにプログラムしたらよいかを説明していく.
基本的にグラフィックスはプリミティブ(基本単位)の集合体である.これはすべてのグラフィックスで共通である.プリミティブとはグラフィックスの各基本要素に当たるPoint,Line,Polygon等のオブジェクトのことである.また,RGBColor,Thicknessの指示子もプリミティブに当たる.
グラフィックスをInputForm(入力形)に変換し,グラフィックスが内部でどう表現されているか見てみる.グラフィックスプリミティブであるPointの座標で各データ点が表されており,また,グラフィックス設定値も与えられている:
| Graphics[list] | 通常の2Dグラフィックス |
| Graphics3D[list] | 通常の3Dグラフィックス |
ユーザ定義のグラフィックスオブジェクトを組み合せ,上記以外のグラフィカルイメージが作成できる.さらに,グラフィックスオブジェクトも式として表すので,標準的なWolfram言語の関数を使いグラフィックスをいろいろ操作できる.
グラフィックスオブジェクトは,Wolframシステムフロントエンドにより,出力の際のグラフィックスとして自動的にフォーマットされる.グラフィックスはPrintコマンドを使った二次的出力として出力されることもある.
GraphicsオブジェクトはWolfram言語で計算されるが,その出力はセミコロンを使うことで表示されない:
| Show[g,opts] | 新しいオプションを opts で指定して,グラフィックスオブジェクトを表示する |
| Show[g1,g2,…] | g1 からのオプションを使って,いくつかのグラフィックスオブジェクトを組み合せて表示する |
| Show[g1,g2,…,opts] | 新しいオプションを opts で指定していくつかのグラフィックスオブジェクトを表示する |
Showは,既存のグラフィックスのオプションを変更するため,あるいは複数のグラフィックスを組み合せるために使うことができる.
グラフィックスプリミティブをもとにしたグラフィックスの作成では,普通,各種の修正操作を繰り返すことで最終的な形を得る.Wolfram言語では修正作業のため2つの方法が用意されている.そのひとつは,グラフィックスにグラフィックス指示子を与える方法である.グラフィックス指示子をグラフィックスプリミティブのリストに加えると,指示内容が続くグラフィックス要素に適用される.すると,グラフィックス単位で描画要素をどう表示するか指定できるようになる.グラフィックス指示子の一例にRGBColorがある.
Polygonグラフィックスプリミティブを含む2Dのグラフィックスオブジェクトを生成する:
InputFormは完全なグラフィックスオブジェクトを表示する:
グラフィックス指示子を与えることで,特定の描画要素をどう表示したらよいかを指定することができる.しかし,多くの場合,グラフィックス全体の構図等の設定は大域的に変更したい.設定を変更するにはグラフィックスオプションを使う.
グラフィックスオプションFrameを加えることで,グラフィックス全体の見栄えを修正することができる:
Showではグラフィックスオプションを指定できる.オプションの設定値をいろいろ変えながら同じプロットデータをもとにグラフィックスをいろいろと再表示でき,違った描画条件下でグラフィックスがどう映るかをすばやく見ていけるので便利である.
注意点として,Showの返すグラフィックスオブジェクトは表示したままのものである.つまり,Showで設定条件を変更した場合,変更した条件もShowの返すオブジェクトに入る.このため,再度同じオブジェクトにShowを使うと,設定条件を変更しない限り,前と同じ仕様で表示されることになる.新たに設定値を指定すれば,もとの値は上書きされる.
グラフィックスオプションの中には,グラフィックスを生成する関数を可視化するオプションとして使えるものもある.右辺にAutomaticを取ることのできるオプションは,可視化関数により特定の値へと分解されることがある.
Wolfram言語は結果のグラフィックスのPlotRangeに対する明示的な値を計算するために,内部アルゴリズムを使う:
| FullGraphics[g] | グラフィックスオプションによって仕様を指定したオブジェクトをプリミティブとしてリスト形式で出力する |
グラフィックスオプションを指定すると,Wolfram言語は指定された通りに,軸等のオブジェクトを自動的に描画する.Axesがよい例である.オブジェクトはグラフィックスプリミティブの特定のリストによってではなく,オプション値によってのみ表される.これらのオブジェクトをグラフィックスプリミティブのリストとして表すことは,ときに有用なものである.関数FullGraphicsはオプションを使わずに,特定のプロットを生成するのに必要なグラフィックスプリミティブのリストを生成する.
FullGraphicsを使い座標軸等のプリミティブも含むグラフィックスオブジェクトを生成する:
| Point[{x,y}] | 座標 x,y に点を描く |
| Line[{{x1,y1},{x2,y2},…}] | 座標点{x1,y1}, {x2,y2}, …を結ぶ線を引く |
| Rectangle[{xmin,ymin},{xmax,ymax}] | 領域を塗り潰した長方形を描く |
| Polygon[{{x1,y1},{x2,y2},…}] | 領域を塗り潰した多角形を描く |
| Circle[{x,y},r] | 半径が r で,中心座標が x,y の円を描く |
| Disk[{x,y},r] | 領域を塗り潰した,半径が r で,中心座標が x,y の円板を描く |
| Raster[{{a11,a12,…},{a21,…},…}] | グレースケール0から1の明暗度の方形セルの配列模様を描く |
| Text[expr,{x,y}] |
関数Plot等によって生成したグラフィックスプリミティブから構成されたグラフィックスオブジェクトは,1つのグラフィックスにまとめることができる.
複数のグラフィックス要素を合成したいときは,要素をリスト形式で入力すればよい.2Dグラフィックスでは,入力した順序で要素が描画される.後で入力したものは先に入力したものの上に重ねて描かれるので注意する.
2つの青い長方形(Rectangle)要素である:
多角形のプリミティブPolygonを2D座標点のリストで入力する.各座標点が多角形の頂点を表し,最初と最後の座標点が結ばれ多角形が完結する.多角形の領域は塗り潰される.
| Point[{pt1,pt2,…}] | 点 pt1,pt2,…からなるマルチポイント |
| Line[{line1,line2,…}] | 線 line1,line2,…からなるマルチライン |
| Polygon[{poly1,poly2,…}] | 多角形 poly1,poly2,…からなる多重多角形 |
多数の点を表すためには,1つのPointプリミティブの内部に座標のリストを置くとよい.同様に,多数の線や多角形も座標のリストのリストとして表すことができる.このように表現すると効率的であり,通常Wolframシステムフロントエンドでより速く描画される.RGBColorのようなグラフィックスプリミティブはプリミティブ全体の集合に一様に適用される.
| Circle[{x,y},r] | 半径 r,点{x,y}を中心とする円 |
| Circle[{x,y},{rx,ry}] | 半軸 rx および ry の楕円 |
| Circle[{x,y},r,{theta1,theta2}] | 円弧 |
| Circle[{x,y},{rx,ry},{theta1,theta2}] | 楕円弧 |
| Disk[{x,y},r]
, etc.
| 塗り潰された円板 |
| Raster[{{a11,a12,…},{a21,…},…}] | グレースケール0から1の明暗度の方形セルからなる縞模様を描く |
| Raster[{{{a11,o11},…},…}] | 不透明度が0から1間までのグレースケールの配列 |
| Raster[{{{r11,g11,b11},…},…}] | RGB値が0から1までの配列 |
| Raster[{{{r11,g11,b11,o11},…},…}] | 不透明度が0から1までのRGB値の配列 |
| Raster[array,{{xmin,ymin},{xmax,ymax}},{zmin,zmax}] | 対角座標が{xmin,ymin}と{xmax,ymax}の長方形領域に, グレースケール幅 zmin から zmax の明暗度の配列の各要素をセルとした縞模様を描く |
グラフィックスオブジェクトは普通ネストしたリストの集合体として与えられる.このとき,各サブリストは描画要素を表す.グラフィックス指示子をこのような集合体に与えると,指示子を加えたリストにおいて,指示子に続くすべての要素(要素がサブリストであればその要素も)が指示子の影響を受ける.しかし,リストの外まで影響は及ばない.
先頭のサブリストにグラフィックス指示子GrayLevelを加え,明暗度を指定しておく:
表示すると,最初のサブリストだけがGrayLevelで指定された明暗度で描画される:
| GrayLevel[i] | グレースケール幅0(黒)から1(白)のグレー値で明暗度を指定する |
| RGBColor[r,g,b] | 赤緑青の各原色についてそれぞれ0から1で色合いを指定する |
| Hue[h] | 幅0から1で色調 h を指定する |
| Hue[h,s,b] | 幅0から1で色調,飽和度,明暗度を指定する |
Wolfram言語は多くの色の名前を直接色指定として受け入れる.Red,Gray,LightGreen,Purple等の色は,評価してRGBColor指定となる変数として実装される.色の名前は色指示子と互換に使うことができる.
最初のプロットは色の名前で,2つ目のプロットは微調整されたRGBColor指定である:
書式Hue[h]を使うと1つのパラメータで色調指定ができ便利である.h で指定する色調値は0から1の値を取る.Hue[h]の値の範囲は赤,黄色,緑,水色,青,紫,そして再び赤に戻る色の輪に対応している.さらに,拡張書式Hue[h,s,b]を使えば,色調だけでなく,色の飽和度と明暗度も指定できる.飽和度1で「原色」が得られ,0に減少していくと「あせた色」が得られる.
RGBColor等のグラフィックス指示子は一度指定したら,その時点から,指定に続く同じリスト内の全要素に適用される.このような無差別に作用する指示子に対して,特定のグラフィックス要素だけに作用する指示子もある.
例えば,PointSize[d]がその一例である.この指示子をグラフィックスオブジェクトに適用すると,すべてのPoint要素が直径 d の円として描画されるようになる.PointSizeでは,直径 d はプロット領域の幅を1としたときの相対的な割合で表す.
| PointSize[d] | すべての点要素を直径 d(相対値で,プロット領域幅に対する割合)で描く |
| AbsolutePointSize[d] | すべての点要素を直径 d(絶対値で,単位はポイント)で描く |
| Thickness[w] | すべての線を w の太さで描く(太さ値は相対値で,プロット領域幅に対する割合) |
| AbsoluteThickness[w] | すべての線を w の太さで描く(太さ値は絶対値で,単位はポイント) |
| Dashing[{w1,w2,…}] | すべての線を破線として描く(破線の区間 w1, w2, …は相対値で指定する) |
| AbsoluteDashing[{w1,w2,…}] | すべての線を破線として描く |
| CapForm[type] | すべての線に,指定されたタイプのキャップを使う |
| JoinForm[type] | すべての線に,指定されたタイプの継ぎ目を使う |
Dashingの描画指定を行うと任意な形の破線が引ける.破線を引く基本的なやり方は短い実線区間と空の区間を交互に繰り返すことである.区間の長さを変えることで破線の形を変える.また,Dashingでは実線の区間と空の区間の単純パターンだけでなく,複雑な区間の組合せパターン(例えば,一点鎖線)を構成することも可能である.
数値サイズ指定を必要とするグラフィックス指示子はTiny,Small,Medium,Large等の値をとることもできる.各指示子に対して,これらの値は微調整されており,人間の目に適した外観を生成するようになっている.
以下はCapFormで利用可能な異なる形状を示す:
CapForm["Butt"]では線が厳密にその終点で終了することを指定する."Square"というキャップは線の終点から線の幅の二分の一だけはみ出した形となる."Round"キャップは線の幅を直径とする半円である.
またJoinForm指示子を使うと,線分間の継ぎ目の形を指定することができる.
JoinFormでは次のような形状が利用できる:
| JoinForm[{"Miter",d}] | 線の幅のほぼ d 倍だけ接合を拡張する |
隣接する線分同士の角度が小さい場合,斜め接合の点は非常に長くなることがある.過剰に長い点は,デフォルトで面取りされた接合に切り取られる.これが起る長さ,斜め接合限界は,5つの頂点の星の点は鋭いがそれより鋭い接合は面取りされるよう設定されている.この限界はJoinFormを使って指定し,厳密にいつ鋭い接合を面取りするかを制御することができる.斜め接合の限界は,接合における点が面取りされる前に,接合の頂点を超えることを許されている線の幅の数である.
| RoundingRadius->r | 角を半径 r で丸めるよう指定する |
Rectangleプリミティブの角はRoundingRadiusオプションで丸めることができる.これは長方形の角の半径を指定するオプションである.実際の丸まり方は,隣接する辺の半分の長さに制限されている.
グラフィックス指示子の使い方の1つは,グラフィックスオブジェクトの構成要素であるグラフィックスプリミティブのリストに直接挿入し局所的に適用させる使い方である.しかし,場合によっては,もっと大域的な描画指定を使いたい.例えば,特定のグラフィックス要素に指示子を適用し,その要素がどこで現れても描画指定を有効にしたい.これは,いわゆる要素の描画スタイルを設定することに相当する.次の表のグラフィックスオプションを使いスタイルを指定することができる.また,各オプションにはスタイルを実際に形作るグラフィックス指示子が割り当てられる.
| PlotStyle->style | Plotで描く全曲線に対してスタイルを指定する |
| PlotStyle->{{style1},{style2},…} | Plotで描く曲線に順番にスタイルを指定する |
| MeshStyle->style | 密度・面グラフにおけるメッシュに対してスタイルを指定する |
| BoxStyle->style | 3Dグラフィックスにおけるプロット境界域を示すボックスに対してスタイルを指定する |
それぞれの曲線に特定のスタイルを与えるように,異なるPlotStyle式を使うことができる:
「スタイル設定のオプション」がいくつか用意されているので,それらを使いプロットするときに特定の描画要素をどう表示するかを指定することができる.さらに,プロット全体の描画様式を決めるオプションも用意されている.
| Background->color | プロットで使う表示面の背景色を指定する |
| BaseStyle->color | プロットに対するベーススタイルを指定し,PlotStyleの影響を受けない要素に影響を与える |
| Prolog->g | プロット開始前に描画するグラフィックスを与える |
| Epilog->g | プロット終了後に描画するグラフィックスを与える |
グラフィックスオブジェクトを構成する各描画要素にはプロット空間における実座標が与えられる.オブジェクトを描画するため,Wolfram言語は実座標を表示用座標に変換する.表示用座標を使うことではじめて各要素を表示面内の適切な位置に配置することができるようになる.
| PlotRange->{{xmin,xmax},{ymin,ymax}} | プロットするデータ,関数値の範囲を示す対角座標を実座標で指定する |
グラフィックス処理でまず行われることは,もとの 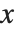 および
および 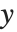 座標のどの範囲をプロット領域として実際に表示するかの決定である.一旦領域が決まったなら,その外にはみ出たグラフィックス要素は「クリップ」され,表示には現れない.
座標のどの範囲をプロット領域として実際に表示するかの決定である.一旦領域が決まったなら,その外にはみ出たグラフィックス要素は「クリップ」され,表示には現れない.
オプションPlotRangeを使い実座標における描画範囲を指定することができる.「プロット仕様の変更」にあるように,デフォルト値はPlotRange->Automaticである.つまり,重要と思われるプロット部分が選択され,その部分だけが描画領域に入れられる.不必要と判断された部分は表示されない.設定をPlotRange->Allとすれば,全領域が描画の対象になる.このオプションで特定範囲を指定することも可能である.
明示的にPlotRangeを指定すると,グラフィックスの断面をズームインすることができる:
| AspectRatio->r | 表示領域の高さ対幅の割合を r とする |
| AspectRatio->Automatic | 実座標系での範囲から縦横比を自動計算する |
使用するモニタやオペレーティングシステムによっても違うが,モニタ表示面で見やすく表示されるには縦横比が適切な値になっていることが必要不可欠である.縦横比を指定するにはオプションAspectRatioを使う.
AspectRatioを指定したからといって,スケールされた座標と表示座標の意味合いが変わるというものではない.後者は0から1の値を取り,1が全表示面の幅を示すことに変わりない.AspectRatioで変わるものは表示領域の縦横の形である.
2Dグラフィックスでは,AspectRatioはデフォルトでAutomaticに設定されている.これは縦横比を固定値に設定する代りに,もとの座標系から決定するものである.もとの座標系の 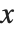 方向への1単位は,最終的な表示において
方向への1単位は,最終的な表示において 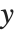 方向の1単位と同じ距離に対応する.このように,もとの座標系で定義したオブジェクトは,「自然な形」で表示される.
方向の1単位と同じ距離に対応する.このように,もとの座標系で定義したオブジェクトは,「自然な形」で表示される.
以下は正六角形に対応するグラフィックスオブジェクトである.デフォルト値のAspectRatio->Automaticでは,最終的な表示領域の縦横比はもとの座標系から求められ,六角形は「自然な形」で表示される:
たまに,グラフィカル要素の表示座標を直接指定することが便利な場合がある.これには {x,y} ではなくスケールされた座標Scaled[{sx,sy}]を使う.スケールされた座標は 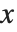 および
および 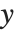 の0から1までで,原点がプロット範囲の左下隅となるよう定義される.
の0から1までで,原点がプロット範囲の左下隅となるよう定義される.
| {x,y} | もとの座標 |
| Scaled[{sx,sy}] | プロット範囲にスケールされた座標 |
| ImageScaled[{sx,sy}] | 表示範囲にスケールされた座標 |
Scaled座標を使うと,長方形は指定されたプロット範囲の中心に位置する原点に置かれる:
ImageScaled座標を使うと,長方形はグラフィックスの中心に置かれる.グラフィックスの中心はプロット範囲の中心とは一致しない:
{x,y},Scaled[{sx,sy}],ImageScaled[{sx,sy}]を使う場合,完全にもとの座標か完全にスケールされる座標かで位置を指定する.しかし,この両方の座標系を組み合せる必要がある場合もある.例えば,長さがプロットの一定分量となっているような線をある点に描画する場合,線の基本的な位置を指定するためにはもとの座標を,線の長さを指定するためにはスケールされる座標を使わなければならない.
Scaled[{dsx,dsy},{x,y}]を使うと,もとの座標とスケールされた座標の両方を使った位置が指定できる.この場合 {x,y} はもとの座標の位置を与え,{dsx,dsy} はスケールされる座標の位置からのオフセットを与える.
| Circle[{x,y},Scaled[sx]] | 半径がプロット範囲の幅にスケールされる円 |
| Disk[{x,y},Scaled[sx]] | 半径がプロット範囲の幅にスケールされる円板 |
| FontSize->Scaled[sx] | プロット範囲の幅にスケールされるフォントサイズの指定 |
Scaledが1つの引数で使える場合
次では,円の半径とフォントの大きさの両方がScaledの値で指定されている:
| Scaled[{sdx,sdy},{x,y}] | もとの座標からスケールされたオフセット |
| ImageScaled[{sdx,sdy},{x,y}] | もとの座標からスケールされた画像のオフセット |
| Offset[{adx,ady},{x,y}] | もとの座標からの絶対オフセット |
| Offset[{adx,ady},Scaled[{sx,sy}]] | スケールされた座標からの絶対オフセット |
| Offset[{adx,ady},ImageScaled[{sx,sy}]] | 画像スケールされた座標からの絶対オフセット |
ほとんどの種類のグラフィックスでは,プロットの座標あるいは全体的な大きさを変更したときに,異なるオブジェクトの相対的な位置が自動的に適応されるようになっていた方がよいだろう.しかし,1つのオブジェクトから別のオブジェクトまでのオフセットが固定されたままの状態に保たれていた方がよい場合もあるかもしれない.例えば,異なるプロットが異なる形式を持つとしても,ある特性に一貫性を持たせたプロットを集めている場合等である.
Offset[{adx,ady},position] を使うと,もとの座標もしくはスケールされた座標で指定される位置から絶対オフセットを与えることにより,オブジェクトの位置を指定することができる.オフセットの単位はプリンタポイント(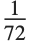 インチ)である.
インチ)である.
プロットにテキストを入れる場合,使用されるフォントの大きさもプリンタポイントで指定する.例えば,10ポイントのフォントは,その基本的な高さが10プリンタポイントの文字である.プロット内部でテキストを動かしたり,テキストサイズにマッチしたシンボルやアイコンを作成したりするときはOffsetを使う.
スケールされた座標を使うと,グラフィカル要素のサイズを表示領域の大きさの割合として指定することができる.しかし,特定のグラフィカル要素を描画する実際の物理的サイズを指定することはできない.もちろんこのサイズは最終的には使用するグラフィックス出力デバイスの詳細に依存するため,Wolfram言語内部で確実に決定することはできない.それでも「グラフィックス指示子とグラフィックスオプション」で説明してあるAbsoluteThickness等のグラフィックス指示子を使うと,特定のグラフィカル要素に対して使用する「絶対サイズ」を指定することができる.この方法で要求するサイズは,すべてではないがほとんどの出力デバイスで有効である(例えば,画像を光学的に投影する場合,その中のグラフィカル要素を同じ絶対サイズに維持することは可能でもなければ望ましくもない).
| Axes->True | 水平・垂直軸を表示する |
| GridLines->Automatic | 方眼線を表示する |
| Frame->True | プロット領域の周りを枠で囲む |
| PlotLabel->"text" | 文字列をプロットのラベルとして表示する |
| Axes->False | 軸の表示を禁止にする |
| Axes->True | |
| Axes->{False,True} | |
| AxesOrigin->Automatic | 軸の交差点を自動決定する |
| AxesOrigin->{x,y} | 軸の交差点を指定する |
| AxesStyle->style | 両軸のスタイルを指定する |
| AxesStyle->{xstyle,ystyle} | それぞれの軸のスタイルを指定する |
| AxesLabel->None | 軸ラベルはなしとする |
| AxesLabel->ylabel | |
| AxesLabel->{xlabel,ylabel} |
Ticksオプションの設定
目盛の描画を自動設定にすると(Ticks->Automatic),目盛の座標値の桁数が最小になるような軸上の位置で主・副目盛を設けてくれる.場合によっては,ユーザ自身で間隔等を指定したいだろう.例えば,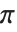 の整数倍の間隔で目盛を打つとか.また,非線形な尺度の軸を使っているときは特別に指定した方がいいだろう.
の整数倍の間隔で目盛を打つとか.また,非線形な尺度の軸を使っているときは特別に指定した方がいいだろう.
| None | 目盛表示を禁止する |
| Automatic | 自動設定の位置に目盛を付ける |
| {x1,x2,…} | 各指定位置に目盛を付ける |
| {{x1,label1},{x2,label2},…} | 各指定位置に目盛を付け,その位置に各ラベルを表示する |
| {{x1,label1,len1},…} | 各目盛の線長をスケールされた座標で指定する |
| {{x1,label1,{plen1,mlen1}},…} | 正方向と負方向の各目盛の線長をスケールされた座標で指定する |
| {{x1,label1,len1,style1},…} | 各目盛にスタイルを指定する |
| func | xmin と xmax に適用して目盛オプションを決める関数 |
特に複雑な目盛を描画するときは,「目盛関数」を用意し,それを使い目盛を描画するよう指定しておく.関数の実行時に,対象軸の最小値と最大値が引数として関数に与えられるので,それらの値に応じた目盛の設定条件が生成できるように関数を記述しておく.
| Frame->False | 枠表示を禁止にする |
| Frame->True | プロット領域を枠で囲む |
| FrameStyle->style | 枠のスタイルを指定する |
| FrameStyle->{{left,right},{bottom,top}} | 枠の各辺のスタイルを指定する |
| FrameLabel->None | 枠に付けるラベルをなくする |
| FrameLabel->{{left,right},{bottom,top}} | 枠の各辺に付けるラベルを指定する |
| RotateLabel->False | ラベルの回転表示を禁止にする |
| FrameTicks->None | 枠の各辺に目盛は打たないものとする |
| FrameTicks->Automatic | 枠の目盛を自動設定の位置に打つ |
| FrameTicks->{{left,right},{bottom,top}} | 枠の各辺に打つ目盛の表示条件を指定する |
プロット軸のオプションAxesを使い,プロットに入れる水平軸と垂直軸の指定が可能である.プロットによっては,描画領域の周りに枠線を引き,その各辺に目盛を打つとよい.それをするには,オプションFrameを使い枠の4辺を軸に見立て必要に応じて目盛を表示させる.枠の4辺の指定順序は底辺から始まり,時計方向に進む.
| GridLines->None | 方眼線を表示禁止にする |
| GridLines->Automatic | 方眼線を自動設定の位置に引く |
| GridLines->{xgrid,ygrid} | 目盛付けの場合と同様に方眼線を指定する |
方眼線の描画設定は目盛の設定とほとんど同じである.目盛の場合と同様に,方眼線にも配置位置を特別に指定できる.また,描画スタイルも指定することが可能である.ただし,方眼線の場合はラベルを付けることはできない.
「プロットの再描画と組合せ」では,GraphicsGridを使って規則的にプロットを配列する方法を説明している.しかし,Insetグラフィックスプリミティブを使うと,プロットをどのように組み合せることも重ねることもできる.
| Inset[obj, pos] | 埋込みがグラフィックスの位置 pos に置かれるよう指定する |
| Inset[obj,pos, opos, size] | obj の点 opos が,グラフィックスの点 pos に位置するよう,オブジェクトを指定の size で描画する |
| Inset[obj,pos, opos, size, dirs] | 埋込みの軸が,方向 dirsに揃うよう指定する |
Wolfram言語はInset内でプロット,任意の2Dおよび3Dグラフィックス,セル,テキストを描画することができる.一般にグラフィックスオブジェクトの表示領域は,Insetの少なくとも1対の辺が触れるようサイズ調整される.
| DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}] | |
f の密度プロットを生成する | |
| ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}] | |
x と y の関数として f の等高線プロットを生成する | |
オプション名
|
デフォルト値
| |
| ColorFunction | Automatic | 陰影付けに使用する色を指定する(Hueでは色のシーケンスが使われる) |
| Mesh | None | メッシュを描くかどうか指定 |
| PlotPoints | Automatic | 各方向における初期のサンプル点の数 |
| MaxRecursion | Automatic | 細分化の最大繰返し数を指定 |
DensityPlotのオプションの例
密度プロットでは,各点の色がプロットされている関数のその点での値を示す.デフォルトでは,関数の値が増加するにつれ,色は黒から中間色の青をへて白へと変わる.しかし一般に,任意の点における値とその色の関係を示す別の「色の対応表」を指定することもできる.オプションColorFunctionを使うと,任意の点での色を見付けるために関数値に適用される関数を指定することができる.色付け関数はGrayLevel,Hue,RGBColor等のWolfram言語の色指示子を返す.一般的な設定は,ColorFunction->Hueである.
ColorDataを使ってアクセスすることのできるグラデーションのリストである:
等高線プロットとは関数の値を「地形図」のようにプロットしたものである.等高線は同じ高さを持つ表面にある点をつなぐ.デフォルトは,等間隔の z 値の列に対応する等高線をもつものである.Wolfram言語で生成される等高線プロットはデフォルトで陰影の度合が高い z ほど明るくなるように陰影処理が施されている.
オプション名
|
デフォルト値
| |
| ColorFunction | Automatic | 陰影付けに使用する色を指定する(Hueでは色のシーケンスが使われる) |
| Contours | Automatic | 等高線の合計数,あるいは等高線のz 値のリスト |
| PlotRange | {Full,Full,Automatic} | |
| ContourShading | Automatic | 陰影処理を使うかどうか. Noneでは領域は空白である.色のリストを与えることができる |
| PlotPoints | Automatic | 各方向における初期サンプル点の合計数 |
| MaxRecursion | Automatic | 細分化の最大反復回数 |
ContourPlotのオプションの例
DensityPlotとContourPlotはどちらも,プロットしている関数がより滑らかになるようより多くのサンプル点を獲得するために,プロット領域を細分化する適応アルゴリズムを使用する.しかし,サンプル点の数は常に有限なので,関数の機能が発揮できないこともある.必要に応じてPlotPointsとMaxRecursionの値を増やし,サンプル点の数を増加することができる.
1点注意したいのは,関数がある特定の領域で急速に変化する場合,Plotにより生成される曲線が不正確になる場合もありうるのに対して,関数があまりに遅く変化する場合は,ContourPlotで生成される等高線の形状は不正確でありえるということである.急速に変化する関数は等高線の決まったパターンを与えるが,ほとんど平坦な関数は不規則な等高線を与える.これは通常PlotPointsまたはMaxRecursionの値を増やすことで解決する.
| Point[{x,y,z}] | x, y, z の座標に点を打つ |
| Line[{{x1,y1,z1},{x2,y2,z2},…}] | {x1,y1,z1}, {x2,y2,z2}, …の各座標点を結ぶ折れ線を引く |
| Polygon[{{x1,y1,z1},{x2,y2,z2},…}] | |
指定座標点が頂点の多角形を描画する (中は塗り潰す) | |
| Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}] | |
対角座標で決まる直方体を描画する | |
| Arrow[{pt1,pt2}] | pt1 から pt2 を向いた矢印 |
| Text[expr,{x,y,z}] | テキストを座標点{x,y,z}に表示する(「テキスト用グラフィックスプリミティブ」を参照のこと) |
2Dグラフィックスではプロットする要素のリストを与えると,各要素が入力順に描画された.このため,後に描画した要素が先に描いたものを隠してしまうこともあった.これに対して,3Dでは,描画要求のあった全要素がまとめられ,立体オブジェクトとして一括で表示される.このため,投影角度によっては,前景にくる要素が背景にまわる要素を隠すことがある.
適当な形の多角形を適切に組み合せることでどんな形の立体オブジェクトでも構築できる.例えば,3Dパラメトリックプロット(ParametricPlot3D)で作った立体面はすべて多角形のリストからなるものである.
| Point[{pt1,pt2,…}] | pt1, pt2, …における点から構成される多点 |
| Line[{line1,line2,…}] | 線 line1, line2, …から構成される多線 |
| Polygon[{poly1,poly2,…}] | 多角形 poly1, poly2, …から構成される複数ポリゴン |
二次元プリミティブの場合と同様に,3Dグラフィックスプリミティブのなかにはより効率的な表現である多座標形式を持つものもある.非常に多数のプリミティブを扱う際に,可能な部分でこのような多座標形式を使うことにより,結果のグラフィックスのメモリ使用量を減らし,描画をずっと速くすることができる.
Polygonの多座標形式を使うことで,非常に多数の三角形を効率的に表現する:
Wolframシステムでは3Dの多角形に任意の設定でいくつの頂点でも持たせることができる.頂点の位置により,結果の多角形は一平面上あるいは一般的な凸でない可能性がある.一平面上ではない多角形を描画する場合は,Wolframシステムは描画する前に,その多角形を定義により平面的な三角形に分解する.
一平面的でない多角形は三角形に分解される.三角形を繋ぐ内部の辺は,Polygonプリミティブの外側の辺のように輪郭が描かれない:
| Cone[{{x1,y1,z1},{x2,y2,z2}}] | 底辺の中心が{x1,y1,z1}で半径が1,頂点が{x2,y2,z2}の円錐 |
| Cone[{{x1,y1,z1},{x2,y2,z2}},r] | 底辺の半径が r の円錐 |
| Cuboid[{x,y,z}] | 対角が座標{x,y,z}と{x+1,y+1,z+1}である単位立方体を作る |
| Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}] | 対角が指定座標にある直方体を作る |
| Cylinder[{{x1,y1,z1},{x2,y2,z2}}] | 終点が{x1,y1,z1}と{x2,y2,z2}である半径1の円筒 |
| Cylinder[{{x1,y1,z1},{x2,y2,z2}},r] | 半径 r の円筒 |
| Sphere[{x,y,z}] | 中心{x,y,z}の単位球 |
| Sphere[{x,y,z},r] | 半径 r の球 |
| Tube[{{x1,y1,z1},{x2,y2,z2},…}] | 指定された点を繋ぐチューブ |
| Tube[{{x1,y1,z1},{x2,y2,z2},…},r] | 半径 r のチューブ |
Cone,Cylinder,Sphere,Tubeは高質の描画を生成するが,使用法はスケール可能である.1つの画像にこれらのプリミティブが何千も含まれることもある.それほど多くのプリミティブを描画するとき,デフォルトでCone,Cylinder,Sphere,Tubeを描画するために使われる点の数を変更する特殊なオプションを使うことにより,描画の効率を向上させることができる.Graphics3Dの"ConePoints" Methodオプションはそれぞれの描画の質を低下させるのに使うことができる.円筒,球,チューブの質も同様にそれぞれ"CylinderPoints","SpherePoints","TubePoints"を使って調整することができる.
2Dのときのように,PointSize,Thickness,Dashingのグラフィックス指示子を使い,3D空間における点や線(Point,Line)の大きさ,太さ,線の形態を指定できる.ただし,3Dでは,それらの条件で指定する長さとは全表示領域の幅に対する割合を示すので注意が必要である.
2Dにおける絶対単位の長さ指定は3Dでも有効である.点の絶対サイズ(AbsolutePointSize),線の絶対太さ(AbsoluteThickness),破線の絶対区間長(AbsoluteDashing)がこれに当たる.
2Dでは,多角形には特定色が常に1つ割り付けられ,その色はRGBColorやOpacity等のグラフィックス指示子により画一的に決められる.これに対して,3Dでは,擬似照明法に基づいたより物理的な手法で多角形の色付けができるようになっている.多角形は色指示子により定義される内色素を引き続き持つが,グラフィックスが描画されたときに見られる最終的な色は,その多角形にあたる光の値により異なる.多角形はデフォルトでは内的に白である.
Wolframシステムで3Dグラフィックスオブジェクトを描画するときに使う線の種類は2つある.ひとつはグラフィックスオブジェクトに含まれている明示的なLineプリミティブの線で,もうひとつは多角形の辺を描くのに使う線である.
後者の線について描画仕様を設定するにはEdgeFormを使いグラフィックス指示子のリストを与える.
| FaceForm[gfront,gback] | 多角形の描画において表面にグラフィックス指示子 gfront を,裏面にグラフィックス指示子 gback を指定する |
3Dグラフィックスでは,どこからどこまでが描画空間なのかを示すため直方体を使いプロット空間の境界を定義している.プロットするオブジェクトはこの直方体(ボックスと呼ぶ)の中に置かれ,デフォルトで,ボックスの輪郭に線が描かれるので(Boxed->Trueの設定が有効時)プロット範囲が視覚的に確認できる.また,オブジェクトがボックスの外にはみ出るようなことがあれば,はみ出た部分は表示されない.
ボックスに包含する 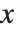 ,
,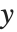 ,
,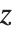 方向の各プロット範囲はオプションPlotRangeを使い指定する.2Dグラフィックスのときのように,デフォルトで自動設定(PlotRange->Automatic)になっており,Wolfram言語内部のアルゴリズムで決定した「重要な部分」だけが描画の対象になる.つまり,部分によってはボックスの外に出てしまい表示されないものもある.そのようなことがないように,すべてを描画対象にするならPlotRange->Allと指定しておく.
方向の各プロット範囲はオプションPlotRangeを使い指定する.2Dグラフィックスのときのように,デフォルトで自動設定(PlotRange->Automatic)になっており,Wolfram言語内部のアルゴリズムで決定した「重要な部分」だけが描画の対象になる.つまり,部分によってはボックスの外に出てしまい表示されないものもある.そのようなことがないように,すべてを描画対象にするならPlotRange->Allと指定しておく.
PlotRangeでプロット範囲を限定する.範囲外になり表示されない部分ができる:
2Dグラフィックスと同様に3Dでも「実座標」と「スケールされた座標」のどちらでもオブジェクトの位置指定ができる.スケールされた座標は書式Scaled[{sx,sy,sz}]で指定し,各座標値は0から1の値を取る.ボックスの包含する空間は右手座標系で表される.
| {x,y,z} | プロットする実空間の座標を指定する |
| Scaled[{sx,sy,sz}] | スケールされた座標を指定する.各座標は0から1の値を取る |
ボックス内の実空間のどこに何を配置するかを指定したなら,次はボックス自体をどう表示させるか指定する.まず,ボックスの縦,横,そして,奥行き長の相対比を決める.これは,2Dプロットにおける縦横比の指定に相当する.3Dでは,縦横比の代りにボックス比のオプションBoxRatiosを使いボックスの各辺(つまり,座標軸の範囲)の相対的な長さを指定する.Graphics3Dオブジェクトの場合は,デフォルトで自動設定になっているので(BoxRatios->Automatic),比は実座標の範囲から決定される.
| BoxRatios->{xr,yr,zr} | ボックスの辺の相対的な長さを指定する |
| BoxRatios->Automatic | 実座標の範囲から計算されるボックス比を使う(Graphics3Dのデフォルト値) |
立体の描画では,どの位置からどの角度で物体を眺めるかといった位置関係を設定する必要がある.位置関係を表す値を「ビューポイント」と呼び,これはオプションViewPointを使い指定する.
「3D曲面プロット」に,よくあるビューポイントの設定例を示したので参考にするとよい.しかし,そこにある設定位置にとらわれる必要はなく,どんな設定をしても構わない.
ビューポイントの指定書式はViewPoint->{sx,sy,sz}である.ここで,値 si はボックス中心を原点({0,0,0})とした特殊な座標系で与えられる.座標の取る値はボックスの最長辺を1とするスケールされた相対値とする.ボックスの他の辺の長さはボックス比(BoxRatios)から決定される.ボックスが立方体ならば,各座標軸は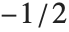 から
から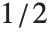 の範囲を取る.ビューポイントは必ずボックスの外になければいけないことに注意する.
の範囲を取る.ビューポイントは必ずボックスの外になければいけないことに注意する.
オプション
|
デフォルト値
| |
| ViewPoint | {1.3,-2.4,2} | 表示するオブジェクトを眺める位置指定 (ビューポイント)をスケールされた特殊座標で指定する |
| ViewCenter | Automatic | 表示領域の中心を示すスケールされた特殊座標系の点 |
| ViewVertical | {0,0,1} | 表示領域における視野垂直方向を示すスケールされた特殊座標系の方向 |
| ViewAngle | Automatic | グラフィックスを見るために使われるシミュレートされるカメラに対する開口部 |
| ViewVector | Automatic | グラフィックスの正規の座標系におけるシミュレートされるカメラの位置と方向 |
3Dグラフィックスでは,描画するオブジェクトをどこから眺めるかだけでなく,表示領域の中にどうオブジェクトを「枠組み」するかを指定する必要もある.後者の設定ではオプションViewCenter,ViewVertical,ViewAngleを使う.
ViewCenterはオブジェクトのどこの点が表示領域の中心に現れるか指定するために使用する.中心点はスケールされた特殊座標(0から1)で与える.例えば,ViewCenter->{1/2,1/2,1/2}と指定すれば,ボックスの中心と表示領域の中心を一致させることになる.ただし,ビューポイントの設定によってはボックスが対照に表示されないため,このViewCenterの設定では必ずしも表示領域の中心にボックスの中心を持っていけない.そのようなときは,自動設定(ViewCenter->Automatic)にした方がよいかもしれない.
次に,ViewVerticalはオブジェクトのどの方向が表示領域で上を向くか指定するのに使う.ViewVerticalの指定は,表示領域上でオブジェクトのどの方向が上を向くかをスケールされた座標で与えることである.デフォルト値はViewVertical->{0,0,1}で,これは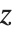 軸が表示領域の垂直方向になるよう表示することを意味する.
軸が表示領域の垂直方向になるよう表示することを意味する.
Wolfram言語は最終的な画像を可視化するために,シミュレートされたカメラの属性を使用する.カメラの位置,方向,向きはViewCenter,ViewVertical,ViewPointオプションで決まる.ViewAngleオプションは,カメラレンズの開口部の幅を指定する.ViewAngleはカメラで見ることのできるViewPointからViewCenterまで伸びた線からの最大角度の2倍をラジアンで指定する.つまり,ViewAngleは画像の一部でズームインするために効果的に使うことができるということである.ViewAngleのデフォルト値は人間の目にとって一般的な視野角である35度である.
ViewAngleを使い,画像の中心を効率的にズームインする:
このように,ViewPoint,ViewCenter,ViewVerticalの一連の設定は,物理的なオブジェクトをどう表示するか指示するために使う.ViewPointはオブジェクトを眺める位置を指定し,ViewCenterはオブジェクトのどこを中心に見るかを指定し,また,ViewVerticalは表示上の垂直方向がオブジェクトのどの方向になるかを指定する.
座標系という点において,ViewPoint,ViewCenter,ViewVerticalの条件設定は一種の座標変換とも考えられる.つまり,3つの条件設定を使い,実空間における物体の各座標を表示領域の座標に変換している,とも考えられる.
| ViewVector->Automatic | オプションViewPointとViewCenterの値を使い, シミュレートされるかめらの位置と向きを指定する |
| ViewVector->{x,y,z} | オブジェクトに使用される座標におけるカメラの位置.カメラの向きはViewCenterオプションで決まる |
| ViewVector->{{x,y,z},{tx,ty,tz}} | カメラの位置と点は,オブジェクトに対して使われる座標で焦点が合わされる |
ViewVectorオプションに可能な値
カメラの位置と向きはViewPointオプションとViewCenterオプションで完全に決めることができる.しかし,ViewVectorオプションは便利な一般化を提供する.ViewVectorではスケールされた座標を使ってカメラの位置と向きを指定する代りに,グラフィックス内でオブジェクトの位置を決めるのに使われる座標系と同じものを使ってカメラの位置を決めることができる.
これもカメラは同じ位置にあるが,異なる向きを向いている.ViewAngleを合せると,グラフィックスの特定の場所をズームインする:
3Dオブジェクトの2Dのイメージを得たなら,次にそれをどう描画するかを指定する.グラフィックスオプションは2Dグラフィックスで使ったものと同じである.つまり,縦横比のオプションAspectRatioを使い最終表示領域の縦横の尺度を変えたり,プロット領域のオプションPlotRegionを限定し表示面全体のどこの領域にイメージを表示させるか等の指定ができる.
グラフィックスをインタラクティブに変更する場合,ビューオプションが変更される.ViewPointを使ってカメラの位置を指定した場合,グラフィックスの回転によりViewPointオプションの値が変更される.ViewVectorを使ってカメラの位置が指定してある場合は,インタラクティブな回転によりそのオプションの値が変化する.どちらの場合も,インタラクティブな回転はViewVerticalオプションの値にも影響を及ぼす.グラフィックスをインタラクティブにズームすることは,ViewAngleオプションの変更と直接呼応する.グラフィックスをインタラクティブにパンすると,ViewCenterオプションの値が変化する.
グラフィックスの表示段階で,立体のイメージが描画領域に対してなるべく大きくなるように尺度が調整される.多くのグラフィックスではこの調整処理は好ましいが,オブジェクトの向きによってはイメージの大きさが変わってしまう場合がある.そのような効果が出てしまうときは,SphericalRegion->Trueの条件を指定する.すると,境界ボックスを包含する球が想定され(ボックスの中心と球の中心はマッチする),最終イメージの尺度調整が球に対して行われるようになる.つまり,球全体が表示領域に収まるようスケールされる.
SphericalRegion->Trueとすると,ボックスの周りに張った球がちょうど表示領域に入るようスケールが調整される:
このように,SphericalRegion->Trueと指定しておくと,オブジェクトの大きさがそのオブジェクトの方向によらず一定となる.1つの立体オブジェクトをいろいろな角度から見たアニメーションを作るときに便利になる.
| SphericalRegion->False | 描画対象をなるべく大きくするように尺度を調整する |
| SphericalRegion->True | 境界ボックスの周りに仮定した球がすべて表示領域に収まるように全体をスケールする |
Wolfram言語ではオブジェクトの照明にさまざまなコンポーネントを指定することができる.その1つは「アンビエント照明」というものであり,オブジェクトに対し一様な陰影処理を施す.この他,「平行光源」はオブジェクトの角度により異なる陰影が施される.「点光源」は空間の1点からすべての方向へ放射される光をシミュレートする.「スポット照明」は「点光源」と似ているが,特定の方向に光の円錐を放射する.平行光源は指定された方向へ向かう光の一様場をシミュレートする.Wolfram言語はこれらすべての光源からの光を一緒にし,特定の多角形の全体照明を決定する.
| {"Ambient",color} | 一様なアンビエント照明 |
| {"Directional",color,{pos1,pos2}} | pos1から pos2までのベクトルに平行な傾向光源 |
| {"Point",color,pos} | 位置 pos の球の点光源 |
| {"Spot",color,{pos,tar},α} | α の半角の開口で目標位置 tar に向けた位置 pos におけるスポットライト |
| Lighting->{light1,light2,…} | 光源の数 |
アンビエント照明を加え,すべての点光源を除去した結果である.Lightingオプションは光源のリストを取る:
Lightingオプションは,Graphics3DあるいはShowのオプションとして使うと,見えているすべてのオブジェクトの照明を制御する.Lightingは特定のオブジェクトに対する照明を指定する指示子としてインラインで使うことができる.継承された照明指定はLighting指示子で置き換えられる.
以下の例ではリストを使い,Lightingの効果が真ん中の球に制限されるようにしている:
これらの彩色指示子を使わなければ,多角形はつや消しの白の面を持つものとされる.つまり,結果的に,入射光のすべてが全方向に一様に反射されることになる.材料にたとえると,表面塗布のない白い紙というところである.
拡散反射とは,面に入射する光はあらゆる方向に一様に散乱する現象をさす.表面がこのような状態にあるときは「さえない色」とか「つや消し」的な面として映る.拡散反射体はランベルト(Lambert)の反射法則に従うことが知られており,反射強度は入射強度に を掛けた値として求まる.ここで
を掛けた値として求まる.ここで 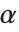 とは入射光と法ベクトルのなす角度である.
とは入射光と法ベクトルのなす角度である.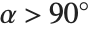 のとき,反射強度はゼロになる.
のとき,反射強度はゼロになる.
鏡面反射では,面は鏡のように入射光を反射する.このため,「放光のある」とか「つやのある」表面として映る.理想的な鏡であれば,入射する光はすべて入射角と同じ角度で反射される.だが,実際の鏡面では,材料によっても程度は違うが,入射光がある程度は散乱するので,反射光が広い角度範囲で分布してしまう.Wolfram言語では強度分布の決定のため,フォン(Phong)の照明モデルを使い,そこで定義される「鏡面指数」と呼ばれる面に固有な定数を適当な値に設定することで分布を計算するようになっている.このモデルは,鏡面指数を 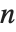 とし,反射角方向から角度
とし,反射角方向から角度 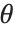 ずれた方向に反射される光の強度は
ずれた方向に反射される光の強度は で与えられる,というものである.
で与えられる,というものである. のとき,反射面は理想的な鏡面になる.また,
のとき,反射面は理想的な鏡面になる.また,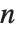 が減少すれば散乱強度が上がるので,表面は放光性を失ってくるし,
が減少すれば散乱強度が上がるので,表面は放光性を失ってくるし, で完全な拡散反射になる.実際の材料では
で完全な拡散反射になる.実際の材料では 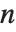 は1から数百の値を取ることが知られている.
は1から数百の値を取ることが知られている.
実際の材料では拡散反射と鏡面反射の両方の効果が有効であり,反射に加え放光するオブジェクトもある.それぞれの種類の発光に対して,オブジェクトは固有の色を持っている.拡散反射の場合,入射光線が白ならば反射光線の色はその物質固有の色となる.白色以外の光を照らした場合は,反射光は入射光の色成分と材料固有の色の積で与えられる色成分の光を放つことになる.同様に,オブジェクトには固有の鏡面反射色がある場合があり,これは拡散反射の色とは異なることがある.鏡面反射の色は,入射光線と内的鏡面色の要素全体の積となる.放光の場合,出される色は内的特性のみにより決まり,入射光線には依存しない.
Wolfram言語では両方の反射効果に個別に固有の色を指定することが可能である.反射光がゼロの材料面には,GrayLevel[0]またはBlackを固有色として指定しておく.また,「白っぽい」色付き表面には,表面の反射率(アルベド)を a としGrayLevel[a]と設定する.
| GrayLevel[a] | アルベド a のつや消し面を指定する |
| RGBColor[r,g,b] | 固有な色のつや消し面を指定する |
| Specularity[spec,n] | |
| Glow[col] | 色 col で放光する面 |
光源と表面の色に設定において,注意しなければいけないことが1つある.それは,どの多角形であってもそこから反射する光の強度は1を越えてはいけない,ということで,もし,1以上に設定した場合は表示がおかしくなる.
Wolfram言語では各種のラベルが3Dグラフィックスにも付けられるようになっている.そのいくつかは2Dグラフィックスのものと同じだが,他は3Dに独特なものである.2Dのラベル設定に関しては「2Dグラフィックスにおけるラベル付け」を参照のこと.
| Boxed->True |
描画対象の周りに直方体(ボックスと呼ぶ)を設け境界線を描く(デフォルト値)
|
| Axes->True | ボックスの各辺に |
| Axes->{False,False,True} | |
| FaceGrids->All | ボックスの各面に方眼線を描く |
| PlotLabel->text | プロットにラベルを付ける |
Graphics3Dのデフォルト設定ではボックス境界線だけが表示されるようになっている.ラベルや軸の書式設定は含まれない:
| BoxStyle->style | 描画スタイルをボックスに適用する |
| AxesStyle->style | 描画スタイルを軸に適用する |
| AxesStyle->{xstyle,ystyle,zstyle} | 各描画スタイルを各軸に適用する |
Axes->Trueと指定すると境界ボックスの辺に軸が描かれる.各軸に平行なボックス辺は4本あるためそのどれにでも軸が描ける.そこで,AxesEdgeの指定をすることで,どの辺を軸にするかを選択することができる.
| AxesEdge->Automatic | すべての軸を描くボックスの辺を内部アルゴリズムで決定する |
| AxesEdge->{xspec,yspec,zspec} | x, y, z の軸を描くボックスの辺を指定する |
| None | 軸表示を禁止にする |
| Automatic | 軸表示用の辺を自動的に決定する |
| {diri,dirj} | 指定した辺に軸を表示する |
例えば,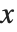 軸を描くには軸に平行なボックスの4つの辺のどれかを選ばなければいけない.各辺は
軸を描くには軸に平行なボックスの4つの辺のどれかを選ばなければいけない.各辺は 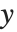 と
と 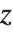 の座標で区別できる.実際の
の座標で区別できる.実際の 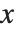 軸にする辺の指定では
軸にする辺の指定では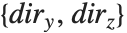 のリスト形式で辺を選択する.
のリスト形式で辺を選択する.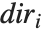 は+1か-1のどちらかの値を取り,前者なら
は+1か-1のどちらかの値を取り,前者なら 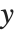 座標(または
座標(または 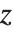 座標)が大きい方の辺が,後者なら小さい方の辺が選択される.
座標)が大きい方の辺が,後者なら小さい方の辺が選択される.
| AxesLabel->None | 軸ラベルを表示しない |
| AxesLabel->zlabel | 文字列を |
| AxesLabel->{xlabel,ylabel,zlabel} | 各文字列を各軸のラベルにする |
AxesLabelを使って各座標軸にラベル付をける.なお,目盛は付けないようにする:
| Ticks->None | 目盛を表示禁止にする |
| Ticks->Automatic | 目盛の表示を自動設定にする |
| Ticks->{xticks,yticks,zticks} | 各軸について個別のグラフィックス指示子を与える |
Ticksオプションの設定
軸の目盛設定では,「2Dグラフィックスにおけるラベル付け」にある2Dグラフィックスの手順が3Dでも有効である.
| FaceGrids->None | 方眼線の表示を禁止にする |
| FaceGrids->All | すべてのボックス面に方眼線を引く |
| FaceGrids->{face1,face2,…} | 任意指定の面 facei だけで方眼線を引く |
| FaceGrids->{{face1,{xgrid1,ygrid1}},…} | 任意指定の面に xgridi,ygridi で指定される方眼線を引く |
3Dグラフィックスでは方眼線はボックスの境界面に描かれる.FaceGrids->Allを指定したなら,すべての面に方眼線が描かれることになる.また,FaceGrids->{face1,face2,…}とすれば,指定面だけに方眼線が描かれる.ここで,各面は書式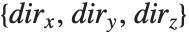 で指定され,パラメータ
で指定され,パラメータ 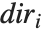 の2つは0でなければならず,最後の1つは+1か-1の値を取る.また,個々の面にどんな方眼線を描くか別々に指定することも可能である.指定には2Dで使ったGridLinesが使える.
の2つは0でなければならず,最後の1つは+1か-1の値を取る.また,個々の面にどんな方眼線を描くか別々に指定することも可能である.指定には2Dで使ったGridLinesが使える.
| Point[{pt1,pt2,…}] | pt1, pt2, …の点からなるマルチポイント |
| Line[{line1,line2,…}] | line1, line2, …からなるマルチライン |
| Polygon[{poly1,poly2,…}] | 多角形poly1, poly2, …からなるマルチポリゴン |
プリミティブの中には,複数要素の形式を持つものもあり,これだと単独のプリミティブよりも速くWolframシステムフロントエンドで処理・描画することができる.多数のプリミティブの場合,複数要素形式を使うことでノートブックファイルのサイズを大きく減少させることもできる.複数要素形式を使うノートブックは使っていない場合よりもサイズが半分以下となり,描画時間も10倍速くなることがある.
| GraphicsComplex[{pt1,pt2,…},data] | data のグラフィックスプリミティブで整数 i として与えられる座標が pti とされるグラフィックスコンプレックス |
メッシュとグラフのように,多数のプリミティブが同じ座標データを共有する場合,GraphicsComplexを使い座標データの一部を取り除くことでより効率的にすることができる.Wolfram言語の表面およびグラフプロット関数の出力は,通常この表現である.
GraphicsComplexは効率的であるだけでなく,インタラクティブに便利である.座標を共有するプリミティブは,その中のひとつがドラッグされてもつながったままである.
どのプリミティブもGraphicsComplexの中で使うことができ,GraphicsComplexは2Dおよび3Dグラフィックスのどちらでも使うことができる.GraphicsComplexの中で,プリミティブの座標位置は指標によりGraphicsComplexの座標データに置き換えられる.
| BaseStyle->value | グラフィックスで有効なテキストスタイルのオプション |
| FormatType->value | グラフィックスで有効なテキストの表記法のオプション |
| "style" | 現行のスタイルシートで指定されたスタイル |
| FontSize->n | フォントサイズ(単位 : ポイント) |
| FontSlant->"Italic" | 斜体フォント |
| FontWeight->"Bold" | 太字フォント |
| FontFamily->"name" | フォント名の指定(例 :"Times","Courier","Helvetica") |
BaseStyle使われる代表的な書式指定
ノートブック用フロントエンドを使っている場合,BaseStyleには現在使っているノートブックのスタイルシートで定義されたスタイル名を設定することができる.そうしておくと,グラフィックスに現れるテキスト要素はすべてそのセルスタイルの書式に従い表示される.また,FontSizeとFontFamilyのようなフォント指定オプションを使い個別にテキスト要素の書式を指定することも可能である.FontSizeには印刷ポイント数でフォントの絶対サイズを指定する.1ポイントは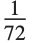 インチに相当する.フォントサイズが数字で指定されているグラフィックス全体の大きさを変えてもテキスト要素の大きさはそれに対応して変わらないことに注意する.テキストの大きさを変えるには再度FontSizeを使い新たな値を指定する必要がある.フォントサイズが,スケールされた量として指定されているプロットの大きさを変える場合は,プロットの大きさが変わるに従ってフォントもスケールされる.FontSize->Scaled[s]の設定では,効果的なフォントサイズはプロットの中の s スケールされた単位である.
インチに相当する.フォントサイズが数字で指定されているグラフィックス全体の大きさを変えてもテキスト要素の大きさはそれに対応して変わらないことに注意する.テキストの大きさを変えるには再度FontSizeを使い新たな値を指定する必要がある.フォントサイズが,スケールされた量として指定されているプロットの大きさを変える場合は,プロットの大きさが変わるに従ってフォントもスケールされる.FontSize->Scaled[s]の設定では,効果的なフォントサイズはプロットの中の s スケールされた単位である.
| Style[expr,"style"] | 式 expr を指定されたスタイルで出力する |
| Style[expr,options] | 式 expr をフォントやスタイルの設定条件に基づいて出力する |
| StandardForm[expr] | 式 expr をStandardForm(標準形)で出力する |
StandardFormで表示する.フォントには12ポイントを使う:
上の例で使った"Section"のスタイルは使っているフロントエンドがノートブック用のときに有効である.テキスト型インターフェースのフロントエンドを使っている場合は,その限りでない.ただし,テキスト型でもFontSize等の個別指定は行える.「テキストとフォントのオプション」に使えるオプションを列挙してあるので参考にするとよい.
テキストのグラフィックスプリミティブTextを使い,2D,3Dグラフィックスの任意の位置にテキスト要素が挿入できる.個別にStyleでフォントを指定しない限り,テキストはグラフィックスのベーススタイルで表示される.
| Text[expr,{x,y}] | 文字列を実座標{x,y}に中央揃えで配置する |
| Text[expr,{x,y},{-1,0}] | 左揃え{x,y}で配置する |
| Text[expr,{x,y},{1,0}] | 右揃え{x,y}で配置する |
| Text[expr,{x,y},{0,-1}] | 上揃え{x,y}で配置する |
| Text[expr,{x,y},{0,1}] | 下揃え{x,y}で配置する |
| Text[expr,{x,y},{dx,dy}] | 実座標{x,y} に横縦のずらし幅{dx,dy} でテキストを配置する |
| Text[expr,{x,y},{dx,dy},{0,1}] | 読み方向が下から上になるようにテキストを垂直に配置する |
| Text[expr,{x,y},{dx,dy},{0,-1}] | 読み方向が上から下になるようにテキストを垂直に配置する |
| Text[expr,{x,y},{dx,dy},{-1,0}] | 文字を上下逆さにした表示にする |
テキスト要素を揃えるには,第2引数の実座標にテキストのどの点を持っていくか指定する.つまり,縦横のずらし幅を与えテキストを揃える位置が実座標にくるようにする.ずらし幅は,領域の中心点を原点{0,0}とし,領域の高さと横幅をともに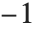 から
から の座標範囲とした特別な相対座標で表す.また,ずらし幅は必ずしも
の座標範囲とした特別な相対座標で表す.また,ずらし幅は必ずしも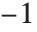 から
から の範囲になくてもよい.
の範囲になくてもよい.
オプション
|
デフォルト値
| |
| Background | None | 背景色 |
| BaseStyle | {} | 段落揃えやフォント書式の指定 |
| FormatType | StandardForm | 表記形 |
Textのオプション
「サウンド」では関数や数値データからサウンドを生成する方法について説明してある.ここでは,サウンドオブジェクトがどういった構造を持ち,形成されているか説明する.
グラフィックスにならい,サウンドもオブジェクトとしてとらえる.サウンドオブジェクトはSoundの頭部が作用した形で記述され,演奏音を表したサウンドプリミティブのリストから構成される.
| Sound[{s1,s2,…}] | サウンドプリミティブのリストからなるサウンドオブジェクトを生成する |
サウンドプリミティブ
| SampledSoundList[{a1,a2,…},r] | サンプルレート r で振幅値のリストからなるサウンドを指定する |
| SampledSoundFunction[f,n,r] | 関数 f を n 個の連続した整数に適用して生成した,サンプルレート r の振幅値からなるサウンドを指定する |
| SoundNote[n,t,"style"] | 音符 n,時間指定 t の指定されたスタイルの音符のようなサウンドを指定する |
最も低次なレベルにおいて,サウンドとは音の振幅標本が連続したもの,またはMIDIイベントの列としてとらえられる.SampledSoundListでは,振幅は数値データのリストで与えられる.また,SampledSoundFunctionを使い関数からサウンドを生成すると,振幅データは関数に整数シーケンスを与え計算により生成される.ただし,実際の生成は演奏するときにだけ行われる.どちらのサウンド形態でも振幅値は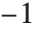 から
から の範囲に入れておかなければいけない.SoundNoteでは,音符のようなサウンドは周波数,期間,振幅,音符のスタイルを表す一連のMIDIイベントとして表現される.
の範囲に入れておかなければいけない.SoundNoteでは,音符のようなサウンドは周波数,期間,振幅,音符のスタイルを表す一連のMIDIイベントとして表現される.
数値リストから,サンプルレート8000のSampledSoundListを生成する:
関数から,サンプルレート8000のSampledSoundFunctionを生成する:
SoundNoteを生成する:
ListPlayを実行するとSampledSoundListのプリミティブが生成され,PlayだとSampledSoundFunctionのプリミティブが生成される.デフォルト通りコンパイル指定が有効なら(Compiled->True),Playの生成するSampledSoundFunctionのオブジェクトはCompiledFunctionによってコンパイルされている.
各種のプリミティブでSoundオブジェクトが形成できたら,次のステップは,それを実際に演奏することである.グラフィックスの場合と同じように,このステップにおける基本処理は,カーネルで作ったサウンドオブジェクトを出力装置で演奏可能な低レベルのデータ形態に変換することである.演奏処理はWolframシステムのフロントエンドや外部プログラムで実行される.
低レベルのデータ表記において,サウンドは振幅を指定した16進数の列データからなる.低レベルに下げる前のカーネル内部処理において,振幅値は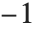 から
から の実数近似値で表されている.低レベルデータを生成するため振幅の実数データに「量子化処理」が施される.量子化処理でオプションの1つにSampleDepthのビット長設定がある.これは何ビットで標本を量子化するかを決めるものである.デフォルトの値は8ビットで(SampleDepth->8),この設定だと振幅は256レベルの量子化が可能である.これは多くの用途で十分なレベル数である.音符ベースのサウンドを低レベルで表現すると,MIDIイベントを時間で量子化したバイトストリームとすることができる.これは音符オブジェクトについてのさまざまなパラメータを指定する.時間の量子化は,プレイバックで自動的に決定される.
の実数近似値で表されている.低レベルデータを生成するため振幅の実数データに「量子化処理」が施される.量子化処理でオプションの1つにSampleDepthのビット長設定がある.これは何ビットで標本を量子化するかを決めるものである.デフォルトの値は8ビットで(SampleDepth->8),この設定だと振幅は256レベルの量子化が可能である.これは多くの用途で十分なレベル数である.音符ベースのサウンドを低レベルで表現すると,MIDIイベントを時間で量子化したバイトストリームとすることができる.これは音符オブジェクトについてのさまざまなパラメータを指定する.時間の量子化は,プレイバックで自動的に決定される.
SampleDepthのビット長設定はPlayおよびListPlayのどちらでも使える.また,サウンドプリミティブに標本化レート(rate)と一緒にビット長(depth)を指定したいときは,{rate,depth}のリスト形式で指定する.
インポートとエキスポート
Exportを使ってサウンドをディスクに書き出す.
インポートされたSoundをディスクに書き出す:
Wolfram言語ではグラフィックスやサウンドをさまざまな形式でエキスポートできる.Wolfram言語でノートブックフロントエンドを使っている場合は,Wolfram言語の提供する機能を使いグラフィックスおよびサウンドを他のプログラムへ直接コピーしたりペーストしたりすることができる.
| Export["name.ext",graphics] | グラフィックスをファイル名から判断される形式でファイルにエキスポートする |
| Export["file",graphics,"format"] | グラフィックスを指定された形式でエキスポートする |
| Export["!command",graphics,"format"] | グラフィックスを外部コマンドにエキスポートする |
| Export["file",{g1,g2,…},…] | グラフィックスの列をアニメーションにエキスポートする |
| ExportString[graphics,"format"] | エキスポートされたグラフィックスの文字列表現を生成する |
| "EPS" |
EPS形式 (
.eps
)
|
| "PDF" |
Adobe Acrobat形式 (
.pdf
)
|
| "SVG" |
スケーラブルベクターグラフィックス (
.svg
)
|
| "PICT" | Macintosh PICT形式 |
| "WMF" |
Windowsメタファイル形式 (
.wmf
)
|
| "TIFF" |
TIFFファイル (
.tif
,
.tiff
)
|
| "GIF" |
GIFと動画GIFファイル (
.gif
)
|
| "JPEG" |
JPEGファイル (
.jpg
,
.jpeg
)
|
| "PNG" |
PNG形式 (
.png
)
|
| "BMP" |
Microsoftビットマップ形式 (
.bmp
)
|
| "PCX" |
PCX形式 (
.pcx
)
|
| "XBM" |
X window systemビットマップ (
.xbm
)
|
| "PBM" |
PBM形式 (
.pbm
)
|
| "PPM" |
PPM形式 (
.ppm
)
|
| "PGM" |
PGM形式 (
.pgm
)
|
| "PNM" |
PNM形式 (
.pnm
)
|
| "DICOM" |
DICOM医療画像形式 (
.dcm
,
.dic
)
|
| "AVI" |
Audio Video Interleave形式 (
.avi
)
|
通常,Wolfram言語外部にグラフィックスをエキスポートする場合はグラフィックスが描画されるサイズを絶対値で指定しておく必要がある.これを行うには,ExportにImageSizeオプションを指定する.
図の幅を印刷用ポイント数 x で印刷したいときは,ImageSize->x と指定する.ImageSize->72xi とすれば,図を xi インチの幅で印刷することができる.幅のデフォルト値は4インチになっている.ImageSize->{x,y}で図が x×y の領域に収まるようにスケーリングを施す.
| ImageSize | Automatic | 印刷用ポイント数での絶対画像サイズ |
| "ImageTopOrientation" | Top | 画像の中でファイルをどのような向きにするか |
| ImageResolution | Automatic | dpi単位での画像の解像度 |
Exportのオプション
多くのプログラムおよびデバイスは,EPS等の解像度に依存しないフォーマットでグラフィックスを取り込むことができる.しかし,中にはグラフィックスを指定された解像度で特別なラスターまたはビットマップフォーマットに変換しておかなければ取り込めないものもある.そのような場合は,Exportにビットマップに必要な解像度をインチ当りのドット数(dpi単位)で指定したオプションImageResolutionを設定する.解像度を低く設定すれば画質は劣るが同時に画像を保存するのに必要なメモリ量も低く抑えることができる.よく使われる解像度はスクリーン表示で72dpi以上,プリンタ出力で300dpi以上である.
| "WAV" | Microsoft wave形式 (.wav) |
| "AU" |
μ
法則エンコード (
.au
)
|
| "SND" | サウンドファイル形式 (.snd) |
| "AIFF" | AIFF形式 (.aif, .aiff) |
Wolfram言語は,グラフィックスやサウンドをエキスポートだけでなく,インポートすることもできる.Importを用いてさまざまな形式でグラフィックスやサウンドを読むことができ,Wolfram言語の式としてWolfram言語に取り入れることができる.
| Import["name.ext"] | ファイル名から推定した形式で,ファイル name.ext からグラフィックスをインポートする |
| Import["file","format"] | 指定された形式でグラフィックスをインポートする |
| ImportString["string","format"] | 文字列からグラフィックスをインポートする |
Importは読み込むデータの形式に依存したさまざまな構造の式を作成する.戻されるデータの処理をしたい場合は,通常その構造を知る必要がある.
| Graphics[primitives,opts] | 解像度に依存しないグラフィックス |
| Image[data,opts] | 解像度に依存するビットマップイメージ |
| {graphics1,graphics2,…} | アニメーショングラフィックス |
| Audio[data] | 音声信号 |
Importによって返された式の構造
