



Plot3D
更多信息和选项









- Plot3D 也被称为曲面图(Surface Plot 或 Surface Graph).
- Plot3D 在绘制域中的 x 和 y 值处计算 f,并连接点 {x,y,f[x,y]} 以形成一个曲面,显示 f 如何随 x 和 y 变化.
- 它对集合
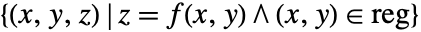 进行可视化.
进行可视化. - 在 fi 运算为除实数以外任何值的点上都会留下间隙.
- Plot3D 将变量 x 和 y 视为局部变量,使用 Block 有效实现.
- Plot3D 有属性 HoldAll, 并仅在对变量 x 和 y 赋给特定数值后计算 f.
- 在某些情况中,在对变量 x 和 y 赋值之前,用 Evaluate 计算 f 更有效.
- 以下封装 w 可用于 fi:
-
Annotation[fi,label] 为 fi 提供注解 Button[fi,action] 当点击曲线 fi 时计算 action Callout[fi,label] 用标注标签函数 Callout[fi,label,pos] 把标注放在相关位置 pos EventHandler[fi,events] 为 fi 定义一般事件句柄 Hyperlink[fi,uri] 使函数成为超链接 Labeled[fi,label] 标签一个函数 Labeled[fi,label,pos] 把标签放在相关位置 pos Legended[fi,label] 在图例中标识函数 PopupWindow[fi,cont] 把弹出窗口附加在函数中 StatusArea[fi,label] 鼠标悬停时显示在状态区域 Style[fi,styles] 使用指定的样式显示函数 Tooltip[fi,label] 把提示条附加在函数上 Tooltip[fi] 使用函数作为提示条 - 封装 w 可用于多层:
-
w[fi] 封装 fi w[{f1,…}] 封装 fi 集合 w1[w2[…]] 使用嵌套的封装 - Callout、Labeled 和 Placed 可用于以下位置 pos:
-
Automatic 自动放置标签 Above, Below, Before, After 曲面周围的位置 {x,y} 靠近位置 {x,y} 的曲面 {x,y,z} 在位置 {x,y,z} {s,Above},{s,Below},… 在位置 s 曲面周围相关位置 {pos,epos} 放在曲面相关位置 pos 的标签 epos - Plot3D 具有同 Graphics3D 相同的属性,并可以附加下列值和变化: [所有选项的列表]
- PlotStyle->None 不绘制曲面,实际上并不消去隐含曲面.
- Plot3D 最初根据 PlotPoints 指定的等间隔的样本点来计算每个函数. 然后使用自适应的算法选择其它的样本点,划分成给定的间隔,划分次数最多为 MaxRecursion 次.
- 应该注意的是,由于使用有限数量的样本点,Plot3D 可能会遗漏函数中的特征. 如果想要检查所得结果是否正确,应尝试增大 PlotPoints 和 MaxRecursion 的设置.
- 设置 Mesh->All,Plot3D 绘制网格线来显示所有子划分.
- 默认设置 MeshFunctions->{{#1&,#2&}} 在每个曲面上绘制一个 x、y 网格线.
- MeshFunctions 和 RegionFunction 的函数变量是 x、y、z. ColorFunction 和 TextureCoordinateFunction 中的函数在默认情况下提供这些自变量的缩放版本.
- ColorFunction、MeshFunctions、RegionFunction 和 TextureCoordinateFunction 在每个曲面上都计算.
- 在默认设置 Exclusions->Automatic 和 ExclusionsStyle->None 下,Plot3D 在它检测到的不连续处断开曲面. Exclusions->None 连接不连续处.
- ScalingFunctions 的可能设置包括:
-
sz 缩放 z 轴 {sx,sy} 缩放 x 和 y 轴 {sx,sy,sz} 缩放 x、y 和 z 轴 - 各缩放函数 si 可以是字符串 "scale" 或 {g,g-1},其中 g-1 是 g 的反函数.
- Plot3D 返回 Graphics3D[GraphicsComplex[data]].
- 影响三维曲面的主题包括:
-

"DarkMesh" 暗色网格线 
"GrayMesh" 灰色网格线 
"LightMesh" 浅色网格线 
"ZMesh" 垂直分布的网格线 
"ThickSurface" 使曲面有厚度 
"FilledSurface" 在曲面下填充
所有选项的列表




范例
打开所有单元 关闭所有单元范围 (26)
采样 (11)
用 PlotPoints 和 MaxRecursion 控制相应的采样:
用 PlotRange 强调感兴趣的区域:
用 Exclusions 删除曲线或分割最后的曲面:
用 RegionFunction 限制曲面在不等式给出的区域上:
用 MeshRegion 来指定变量的取值范围:
标签和图例 (6)
选项 (103)
BoundaryStyle (6)
BoundaryStyle 应用到 RegionFunction 分割的奇点上:
BoundaryStyle 不应用到 Exclusions 分割的奇点上:
ColorFunction (6)
EvaluationMonitor (2)
Filling (4)
MeshShading (4)
NormalsFunction (3)
PlotLegends (5)
PlotStyle (5)
RegionFunction (4)
ScalingFunctions (9)
应用 (17)
基本应用 (7)
用 MeshShading 在曲面上生成空洞以查看其内部结构:
用 MeshFunctions 指定使用的切面:
函数特征 (2)
用 RegionFunction 产生一个缺口以帮助理解极限处的情况:
用 MeshFunctions 突出显示函数 ![]() 的局部极值:
的局部极值:
属性和关系 (8)
Plot3D 在需要的位置取样更多的点:
Plot3D 是 ParametricPlot 的一个特例:
对于绘制数据用 ListPlot3D:
ComplexPlot3D 绘制作为高度的函数幅度,使用相位绘制颜色:
对一元函数用 Plot:
对于平面参数曲线和区域用 ParametricPlot:
对于隐式曲面和区域用 ContourPlot3D 和 RegionPlot3D:
对于密度图和等高图用 DensityPlot 和 ContourPlot:
技术笔记
-
▪
- 三维曲面绘图
历史
1988年引入 (1.0) | 在以下年份被更新:2007 (6.0) ▪ 2010 (8.0) ▪ 2012 (9.0) ▪ 2014 (10.0) ▪ 2016 (11.0) ▪ 2017 (11.1) ▪ 2019 (12.0) ▪ 2021 (13.0)
文本
Wolfram Research (1988),Plot3D,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Plot3D.html (更新于 2021 年).
CMS
Wolfram 语言. 1988. "Plot3D." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/Plot3D.html.
APA
Wolfram 语言. (1988). Plot3D. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Plot3D.html 年
BibTeX
@misc{reference.wolfram_2025_plot3d, author="Wolfram Research", title="{Plot3D}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Plot3D.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_plot3d, organization={Wolfram Research}, title={Plot3D}, year={2021}, url={https://reference.wolfram.com/language/ref/Plot3D.html}, note=[Accessed: 08-January-2026]}