数表現と数値評価

• 大きな整数および高精度近似数は，機械整数の長さに応じて，または桁を基底とした配列として保存される．

• 精度は内部で浮動小数点数として保存されている．

• IntegerDigits，RealDigitsおよび関連する基底変換関数は，帰納的分割統治アルゴリズムを使用する．これと同様のアルゴリズムが数値の入出力に使われる．

• Nは，要求された全体の精度を得るため，内部作業精度の増加に適応型手続きを使用する．

• Floor，Ceilingおよび関連する関数は，厳密な入力から厳密な出力を生成するために，Nと同様に適応型手続きを使用する．

基本算法

• 大きな整数および高精度近似数の積はインターリーブされた基礎的な法，カラツバ(Karatsuba)法，3ウェイToom–Cook法，および数論変換法を使用している．

• 特定のアーキテクチャのための機械語の最適化はGMPを使って行う．

• 整数のベキは左右二進法分解によるアルゴリズムを使用している．

• 近似数の逆数および有理ベキは，ニュートン法を使用する．

• 厳密な根は数値近似から始めている．

• マシン精度に等しくない近似数値を使う算法ではデフォルトで有意算法が使用されている．

擬似乱数

• RandomReal，RandomInteger等の関数に対するデフォルトの乱数ジェネレータでは，セルオートマトンベースのアルゴリズムを使用する．

数論関数

• GCDはHGCD法，ジェベリーン・ソレンソン・ウェーバー(Jebelean–Sorenson–Weber)加速GCD法，それにユークリッド法および2のベキ乗逐次除去に基づくアルゴリズムを組み合せて使用している．

• PrimeQは最初に小さい素数を使用して除算可能かを試し，次にミラー・ラビン(Miller–Rabin)強擬似素数テストベース2およびベース3を使用し，次にルーカス(Lucas)テストを試みる．

• この方式をパスする既知の合成数はない．

• 素数性証明パッケージはすべての 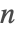で正しいことが証明されている．アルゴリズム自体はかなり遅いものであるが素数かどうかを確認できる．

• FactorIntegerは小さな素数を試験的に除算してみる方法とポラード(Pollard) ，ポラード・ロー，楕円曲線および二次ふるい法を交互に試す．

• PrimeおよびPrimePiは疎キャッシングおよびふるいを使用する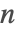． が大のときは，素数密度の漸近推定に基づきPrimePiでラガリアス・ミラー・オドリスコ(Lagarias–Miller–Odlyzko)アルゴリズムが使用され，反転してPrimeを求める．

• LatticeReduceはレンストラ・レンストラ・ロヴァッツ(Lenstra–Lenstra–Lovasz)の格子算法アルゴリズムのStorjohannの変形を使用する．

• 要求された項数を得るため，ContinuedFractionは自己再開始分割統治アルゴリズムを用いた修正レーメー(Lehmer)の間接法を使用して，各ステップで要求される数値精度を削減する．

• ContinuedFractionは，再帰関係を使用して二次無理数の周期連分数を得る．

• FromContinuedFractionは，分割統治アルゴリズムで最適化された反復行列乗法を使用する．

組合せ関数

• ほとんどの組合せ関数は疎キャッシングおよび繰返し計算を使用する．

• Binomialおよび関連する関数は，分割統治アルゴリズムを使用して，部分積の桁数を調整する．

• n!は素数ベキへの動的分解に基づいたSchönhageの アルゴリズムを使う．

• Fibonacci[n]は 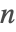の二進数列に基づく反復法を使用する．

• PartitionsP[n]は 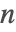が小さいときはオイラー(Euler)の五角式を使用し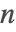， が大きいときは直接的なハーディ・ラマヌジャン・ラーデマッハー(Hardy–Ramanujan–Rademacher)法を使用する．

• ClebschGordanおよび関連する関数は一般超幾何級数を使用する．

• ベルヌーイ(Bernoulli)数は，その数の指標により再帰方程式あるいはFillebrownアルゴリズムを使って計算される．

• ベルヌーイ多項式は，ベルヌーイ数から構築される．

初等超越関数

• 指数および三角関数はテイラー級数，引数を倍にする安定な反復法および種々の関数公式を使用する．

• 対数および逆三角関数はテイラー級数と関数公式を使用する．

数学定数

• 一定サイズより小さい定数の値は一度計算されるとキャッシュされる．

• 二進分割は，適用可能な場合は定数の計算の部分分割に使用される．

• Piは，チュドノフスキー(Chudnovsky)式を使用して計算される．

• Eは級数展開から計算される．

• EulerGammaは，ブレント・マクミラン(Brent–McMillan)アルゴリズムを使用する．

• Catalanは，一般化された超幾何学的総和を使って計算される．

特殊関数

• マシン精度を考慮して，ほとんどの特殊関数はWolframシステムにより導かれた有理ミニマックス近似を使用する．以下の注は主に任意精度に適用される．

• 直交多項式は多項式では安定反復式，一般には超幾何関数を使用する．

• Gammaは漸化式，関数方程式およびビネット(Binet)漸近式を使用する．

• 不完全ガンマおよびベータ関数は超幾何級数および連分数を使用する．

• PolyGammaはオイラー・マクローリン(Euler–Maclaurin)総和，関数方程式，漸化式およびフルヴィッツ(Hurwitz)のゼータ関数の関数方程式を使用する．

• PolyLogはオイラー・マクローリン総和，不完全ガンマ関数での展開および数値積分を使用する．

• Zetaおよび関連する関数はオイラー・マクローリン総和および関数方程式を使用する．臨界辺ではリーマン・ジーゲル(Riemann–Siegel)式も使用される．

• StieltjesGammaはゼータ関数積分表現の数値積分に基づいたカイパー(Keiper)のアルゴリズムとベルヌーイ数を使った交互級数総和を使用する．

• 誤差関数は不完全ガンマ関数と超幾何関数を使用して評価される．

• 指数積分に関連した関数はすべて不完全ガンマ関数を使用して評価される．

• 逆誤差関数は二項検索および高次一般化ニュートン(Newton)法を使用する．

• ベッセル(Bessel)関数は級数および漸近展開を使用する．整数次に関しては安定な前進漸化式を使用することもある．

• 超幾何関数は関数方程式，安定な漸化式，級数展開，漸近級数およびパデ(Padé)近似を使用する．NSumおよびNIntegrateによる方法を使用することもある．

• ProductLogは有理近似および漸近展開から始まる高次ニュートン法を使用する．

• 楕円積分は下降ガウス(Gauss)変換を使用して評価される．

• 楕円シータ関数は級数項の反復評価による級数総和とモジュラ変換を使用する．

• 他のほとんどの楕円関数は算術幾何平均法を使用する．

• マシュー(Mathieu)関数はフーリエ級数を使用する．マシュー特性関数はブランク(Blanch)のニュートン法の一般化形式を使用する．

数値積分

• NIntegrateはシンボリックなプリプロセスにより関数の対称性を考慮して区分関数を単一の区分関数に展開し不等式によって指定される区域を単体に分解する

• Method->Automaticにより一次元ではNIntegrateは"GaussKronrod"を使用し，それ以外では"MultiDimensional"を使用する．

• もしMaxPointsの設定が明示的に与えられている場合はNIntegrateはデフォルト値ではMethod->"QuasiMonteCarlo"を使用する．

• "GaussKronrod"：クロンロッド(Kronrod)点での評価に基づく誤差評価適応型ガウス積分．

• "DoubleExponential"：非適応型二重指数数値積分．

• "Trapezoidal"：初等台形法．

• "Oscillatory"：三角関数およびベッセル関数を含む積分処理のための変換．

• "MultiDimensional"：適応型ゲンツ・マリック(Genz–Malik)アルゴリズム．

• "MonteCarlo"：非適応型モンテカルロ．

• "QuasiMonteCarlo"：非適応型ハルトン・ハマーズリー・ウォズニアコスキー(Halton–Hammersley–Wozniakowski)アルゴリズム．

数値総和および乗積

• もしレシオテストの結果が1に等しくない場合は，ウィン(Wynn)・イプシロン法が数列の部分和または部分積に適用される．

• それ以外はオイラー・マクローリン総和がIntegrateまたはNIntegrateとともに使用される．

微分方程式数値解法

• 常微分方程式には，NDSolveはデフォルトでLSODA手法を用い，非剛性アダムス(Adams)法と剛性ギア(Gear)後退微分法とを交互に切り換える．

• 線形境界値問題ではゲルファンド・ロクチェフスキー(Gelfand–Lokutsiyevskii)追跡法が使用される．

• 微分代数方程式では反復BDF（後退微分式）とニュートン反復法に基づいたIDAが使われる．

• 次元の偏微分方程式では線分法が使用される．

• NDSolveは文献に載っているほとんどの既知のアルゴリズムを網羅する明示的Method設定をサポートする．

• NDSolveとその関連関数のコードは約1400ページに及ぶ．

近似方程式の解法および最適化

• 多項式の根はジェンキンス・トラウブ(Jenkins–Traub)アルゴリズムに基づく．

• 疎な線形システムではSolveおよびNSolveはほとんどの場合はマルコウィツ(Markowitz)積とガウス分解に基づいて複数の効果的数値解法を使用する．(約250ページのコード)．

• 代数方程式系では，NSolveは効率的な単項式の順序付けを用いて数値グレブナー(Gröbner)基底を計算し，固有系法で数値根を抽出する．

• FindRootは減衰ニュートン法，割線法およびブレント法を使用する．

• Method->Automaticで初期値が2つの場合は，FindMinimumはブレントの主軸法を使う．各変数に初期値がそれぞれ1つときは，FindMinimumは大きな系用にメモリ変形を限定したBFGS擬似ニュートン法を使う．

• もし最小化する関数が平方和である場合は，FindMinimumはレベンベルグ・マルカン(Levenberg–Marquardt)法(Method->"LevenbergMarquardt")を使用する．

• 制約条件付きの場合，FindMinimumは内点法を使う．

• LinearProgrammingはシンプレックス法と改良シンプレックス法を，またMethod->"InteriorPoint"では主双対内点法を使う．

• 線形の場合は，NMinimizeとNMaximizeはLinearProgrammingと同じ方法を使う．非線形の場合は，特に整数変数が存在するときは，微分進化法で補強されたネルダー・ミード(Nelder–Mead)法が用いられる．

• LeastSquaresはLAPACKの最小二乗関数を使用する．

データ処理

• Fourierはデータ長を素因数分解するFFT法を使用する．素因数が大きい場合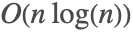， 漸近複雑度の維持のため高速たたみ込み法が使用される．

• 実数入力に対してはFourierは実変換法を使用する．

• ListConvolveおよびListCorrelateは，可能な場合はFFT法を使用する．厳密な整数入力に対しては，大きな整数の乗算という問題を軽減するためにバイナリ分割が使用される．

• InterpolatingFunctionはラグランジュ(Lagrange)またはエルミート(Hermite)補間多項式を構成する分割差分を使用する．

• Fitは特異値分解を使う．FindFitは線形最小二乗法には同じく特異値分解を，非線形最小二乗にはレベンベルグ・マルカン法を，その他のノルムには一般的なFindMinimum法を使う．

• CellularAutomatonはビットパック並行操作をビットスライスで使うことが多い．基本ルールでは，並列操作は最適化されたブール関数を使って実装され，総和型ルールではジャストインタイムコンパイルのビットパック表が使われる．二次元では，ムーア近傍に作用する二色の静止ルールおよび無限背景を持つ状態に対して，アクティブなクラスタだけを更新し，可能な場合は疎なビットパック配列が使われる．

近似数値線形代数

• 機械精度行列の処理は，通常は特殊内部表現に変換される．

• パターンを含む規則を持つSparseArrayは，連結した配列要素を見付けるために円筒代数分解を使う．疎な配列は，任意のランクのテンソル用に一般化された圧縮された疎な行の形式を使って内部的に保存される．

• 密な配列の場合は，適当であれば任意精度に拡張されたLAPACK法が使われる．

• 特定の機械アーキテクチャの最適化にはBLAS（基礎線形代数サブルーチン）技術が使われる．

• LUDecomposition，Inverse，RowReduceおよびDetは部分ピボッティングによるガウス消去法を使用する．LinearSolveも同じ方法を使用し，高精度を得るため適応的に反復計算させる．

• 疎な配列の場合は，LinearSolveはUMFPACKマルチフロンタル直接ソルバ法を使い，Method->"Krylov"は不完全なLU因数分解で前提条件を付けられたクリロフ(Krylov)の反復改善法を使う．高精度数については適応的な反復法を用いる．EigenvaluesとEigenvectorsはARPACKアーノルディ(Arnoldi)法を使う．

• SingularValueDecompositionはギブンズ(Givens)回転のQR法を使用する．PseudoInverse，NullSpaceおよびMatrixRankはSingularValueDecompositionに基づいている．疎な行列では，アーノルディ法が使われる．

• QRDecompositionはハウスホルダー(Householder)変換を使用する．

• SchurDecompositionはQR反復法を使用する．

• MatrixExpは可変パデ近似法を用い，Paterson–Stockmeyer法またはクリロフの部分空間近似を用いて有理行列関数を評価する．

線形代数の厳密数値解

• InverseおよびLinearSolveは数値近似に基づく効果的な行消去を使用している．

• Modulus->n によりモジュラ・ガウス消去法を使用する．

• Detはモジュラ法および行消去法を使用し，中国剰余定理により結果を構成する．

• Eigenvaluesは特性多項式補間により計算される．

• MatrixExpはピュツァー(Putzer)法またはジョルダン(Jordan)分解を使用する．

多項式処理

• 一変数多項式ではFactorは変形カントール・ザッセンハウス(Cantor‐Zassenhaus)法を使用して素数を法として分解し，ヘンゼル(Hensel)構成と試し割りにより整数上の因子を決定する．

• 代数的数体上の因数分解は有理数上の原始関数を見付け，トレーガー(Trager)法を使用することにより実現される．

• 多変数多項式ではFactorは適度に選択された整数を一変数を除いて代入し，結果の一変数多項式を分解し，ワン(Wang)法の使用で多変数因子を構成することにより実行される．

• 一般多項式処理だけを扱うFactorの内部コードは約250ページに渡る．

• FactorSquareFreeはまず微分を実行し，GCDを逐次的に計算することにより実行される．

• Resultantは明示的部分終結式多項式剰余列または中国剰余定理に伴うモジュラ列を使用する．

• Apartはパデ(Padé)法または未定係数法を使用する．

• PolynomialGCDとTogetherは通常はズィッペル(Zippel)の疎モジュラ法を含むモジュラ法を使用するが，部分終結式多項式剰余列を使用することもある．

• 多変数多項式の場合は中国剰余定理が疎な補間法とともに用いられる．

記号線形代数

• RowReduce，LinearSolve，NullSpaceおよびMatrixRankはガウスの消去法に基づいている．

• Inverseは小行列式展開と行消去を使用する．ピボットは単純な式を目標として発見的に選ばれる．

• Detは小規模行列には直接小行列式展開を，大規模行列にはガウスの消去法を使用する．

• MatrixExpはまず固有値を求め，それからピュツァー法を使用する．

• さまざまな関数のゼロテストは，数式変換および乱数値を変数に代入した後に区間数値近似を使用して実行される．

方程式の厳密解法と簡約

• 線形方程式ではガウスの消去法および他の線形代数での方法が使用されている．

• 代数的数値を表すRootオブジェクトは通常は孤立していて，実証されている数値解法により処理される．ExactRootIsolation->Trueにより，Rootは実根ではデカルトの符号規則に基づいた連分数のアルゴリズムが使用され，複素根ではコリンズ・クランディック(Collins‐Krandick)法が使用される．

• 多項式からなる単一の方程式ではSolveは四次までは明示的式を使用して，多項式をFactorおよびDecomposeで簡約化を試み，巡回および他の特殊多項式を見出す．

• 多項式からなる連立方程式ではSolveはグレブナー基底を構成する．

• SolveおよびGroebnerBasisは改良ブッフバーガー(Buchberger)法を使用する．

• 非多項式からなる方程式ではSolveは変数変換および多項式条件の付加を試みる．

• Solveと関連関数のコードは約500ページに渡る．

• 多項式系には，Reduceは実数領域には円筒代数分解を，複素数領域にはグレブナー基底法を使う．

• Reduceは代数関数を使って同値純多項式系を構築する．また，Reduceは超越関数を用いて，超越条件を持つ多項式系を生成し，次に関数関係と逆画像情報のデータベースを用いてこれを簡素化する．区分関数を利用すると，Reduceはシンボリックな展開を行い，連続関数の集まりを作成する．

• 一変数の超越方程式では，Reduceは解を超越Rootオブジェクトとして表す． 実数上の指数・対数関数方程式では，Reduceは厳密は指数・対数根分離アルゴリズムを使う．有界の実数あるいは複素数領域上の解析関数では，Reduceは有効な数値メソッドを使って根を見付ける．初等関数では，区間演算メソッドを使って根の数と位置の両方の正当性が完全に実証される．非初等関数では根の数の正当性は数値積分の正確さに，根の位置の正当性はWolframシステムの有効桁演算により提供される確度推定の正確さに依存する．

• CylindricalDecompositionは，有向系に関してはコリンズ・フォング(Collins‐Hong)法とブラウン・マッカラム(Brown‐McCallum)射影法を用い，その他のものにはフォング射影法を用いる．CADの構築は，厳密な代数的数の計算によって裏付けられた有効性が証明されている数値を使った，ストゼボンスキー(Strzebonski)の系図に基づいたアルゴリズムが用いられる．零次元の系にはグレブナー基底法が用いられる．

• GenericCylindricalDecompositionでは，より簡単な投影演算子を使い，有理数の標本店を持つセルだけを構築する，簡素化されたCADが使われる．

• ディオファンタス(Diophantus)系に関しては，Reduceはエルミートの正規形を用いて線形方程式を解き，線形不等式に関してはContejean‐Devie法を用いる．また，単変数整方程式には改良型のCucker‐Koiran‐Smale法を，二変数二次方程式にはHardy‐Muskat‐Williams法を楕円に，ペル(Pell)その他の事例には古典的手法を用いる．Reduceは，トゥエ(Thue)方程式のためのTzanakis‐de Weger法を含むおよそ25のクラスのディオファンタス方程式のための特化したアルゴリズムを含む．

• 素数モジュラスでは，Reduceは線形方程式には線形代数を，整方程式には素体上のグレブナー基底を用いる．複合モジュラスでは，整数に対してエルミートの正規形とグレブナー基底を用いる．

• Resolveは主としてReduceからのアルゴリズムの最適化されたサブセットを用いる．

• Reduceと関連関数には，およそ350ページのWolframシステムコードとおよそ1400ページのCコードが使われている．

厳密な最適化

• 線形の場合，MinimizeとMaximizeは厳密な線形計画法を用いる．多項式の場合は，円筒代数分解が用いられる．閉じた，あるいは有界のボックスにおける解析的な場合では，ラグランジュの未定乗数法に基づいたメソッドが使われる．

• 変数が整数の有界の線形の場合，MinimizeとMaximizeは前処理として格子算法による簡約を行った分枝限定法を整数線形計画法に用いる．

• 区分関数はシンボリックに展開され，それぞれのケースが別々の最適化問題として処理される．

簡約化

• FullSimplifyは，自動的に約40種類の一般代数変換および約400種類の特定の関数規則を適用する．

• 一般超幾何関数は約70ページのWolfram言語変換則を使用して簡約される．これらの関数はWolframシステムでの多くの解析演算の基礎となる．

• FunctionExpandは拡張ガウス法を使用して，引数が 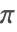の有理数倍であるような三角関数を展開する．

• SimplifyおよびFullSimplifyは，必要に応じて結果をキャッシュする．

• 仮定によって変数が実数に指定されると，多項式制約条件は円筒代数分解によって処理される．一方線形制約条件には，シンプレックス法またはLoos‐Weispfenningによる線形限定子消去法が用いられる．厳密な多項不等式にはストゼボンスキーの一般的なCAD法が用いられる．

• 仮定として多項式間の方程式が含まれる場合，グレブナー基底が使用される．

• 非代数的関数では，関係データベースが使用され，関数値の領域を引数の領域から決定する．結果の領域が半代数集合に対応する場合は，常に多項式指向のアルゴリズムが使用される．

• 整数関数では，数百に及ぶ数論の定理がWolfram言語の規則の形式で使用される．

• 区分関数は区分の分布性に基づく再帰的な方法で処理される．

微積分

• 微分は，キャッシングを使用して部分的な結果が再びコンパイルされることを避ける．

• 不定積分では被積分関数と積分ともに初等関数，指数積分関数，多対数および他の関連した関数で表される場合には拡張リシュ(Risch)法が使用される．

• 他の不定積分には発見的簡約化およびそれに続くパターンマッチングが使用される．

• Wolframシステムで使用されているアルゴリズムは例えばグラドシュテーン・ライジック(Gradshteyn‐Ryzhik)のような標準的参考書に掲載されている不定積分はすべてカバーしている．

• 特異点を含まない定積分は通常は不定積分の極限を取ることにより評価される．

• 他の多くの定積分はマリチェフ・アダムチック・メリン(Marichev‐Adamchik‐Mellin)変換法により処理される．その結果は多くの場合，マイヤー(Meijer)G関数で表され，スレーター(Slater)の定理により超幾何関数に変換される．

• 不等式で定義される多次元の領域での積分は，繋がっていない円柱，三角形のセルに繰り返し分解することにより計算される．

• Integrateは約500ページの Wolfram言語コード，約600ページのCコードからなる．

微分方程式

• 定数係数の線形方程式システムは行列指数化により解かれる．

• 係数変数を持ち，解が基本関数とその積分で表せる二階線形方程式はコバシック法を用いて解かれる．

• 高階線形方程式はAbramovおよびBronsteinのアルゴリズムで解く．

• 有理係数を持つ線形方程式はメリン変換法を用いて特殊関数によって解く．より一般的な係数を持つ式は，可能な場合いろいろな変換法によって簡略化される．

• 有理関数の係数を持つ，解が有理関数として与えられる線形方程式の系はAbramov‐Bronstein消去法で解く．

• 可能ならば，非線形方程式は変数の変換，シンメトリー消去法によって解かれる．一階方程式には多くの従来の技術が用いられる．二階方程式と系には因子積分とBocharov法が使われる．Abel方程式は相当クラスを決定するために不変量を計算することにより解かれる．

• 区分関数は通常，境界値問題の集合に分解することで解かれる．

• WolframシステムのアルゴリズムはKamkeのような標準的な参考書にある一般的な微分方程式のほとんどすべてをカバーしている．

• 線形，準線形偏微分方程式では変数分離および対称消去法が使用される．

• 一階非線形偏微分方程式では，ルジャンドル(Legendre)，オイラーや他の変換によって簡略化されることにより完全な積分が計算される．

• 微分代数方程式では，核ベキ零分解により特異部分を分離することに基づいたアルゴリズムを使う．

• 高次の微分方程式に関しては，因数分解のアルゴリズムとしてBronsteinおよびvan Hoeijのテクニックを使用する．

• DSolveは約300ページのWolfram言語コードと約200ページのCコードからなる．

総和と乗積

• 多項式級数はベルヌーイおよびオイラー多項式を使用して総和が取られる．

• 有理，超幾何， 有理，およびその他のタイプの不定，有限，無限和には，一般化された超幾何関数で答を返すアダムチック法を含む特殊なアルゴリズムが使われる．

• 多ガンマ関数を含む級数は積分表現を用いて総和が取られる．

• ディリクレ(Dirichlet)および関連する級数はパターンマッチングにより総和が取られる．

• 無限級数ではダランベール(d’Alembert)およびラーベ(Raabe)収束テストが使用される．

• Wolframシステムで使用されているアルゴリズムは，例えばグラドシュテーン・ライジックのような標準的参考書に掲載されている総和の少なくとも90%をカバーしている．

• 乗積は，パターンマッチングの他，多項式，有理， 有理，超幾何，定期等のクラスを使って実行される．

• SumおよびProductは約100ページを超えるWolfram言語コードからなる．

級数および極限

• Seriesは引数を級数展開した関数を反復的に級数展開して評価される．

• 極限は級数や他の方法を使用して求める．

• 極限および級数における仮定には，RefineおよびSimplifyに組み込まれている「一般的化された仮定の上での目的評価」のメカニズムを使う．

再帰方程式

• RSolveは定数係数を持つ線形方程式系を行列のベキ乗を使って解く．

• 多項式係数を持つ，解が超幾何的に与えられる線形方程式はvan Hoeij法で解く．

• 有理関数の係数を持つ，解が有理関数として与えられる線形方程式の系はAbramov‐Bronstein消去法で解く．

• 非線形方程式は変数の変換，Göktaşシンメトリー消去法，あるいはGermundsson三角ベキ法が使われる．

• Wolframシステムのアルゴリズムは，数学の文献でこれまでに論じられたほとんどの常差分， 階差分，関数差分方程式をカバーしている．

• 差分代数方程式では，核ベキ零分解による特異部分の分離に基づく方法が使われる．

グラフィックス

• 3Dグラフィックスの描画は，利用可能ならばハードウェアアクセラレーションを使うよう最適化される．

• 3D描画では多角形を分類するのに2つの異なる方法が使われる．透過性のないグラフィックスでは，ハードウェアで加速されるデブスバッファが使われる．それ以外では，どのビューポイントからでも多角形を分割および分類するバイナリ空間分割(BSP)木が使われる．BSP木は生成するのに時間がかかりハードウェアで加速されないが，多角形をサポートする最も一般的な機能を提供する．

• ノートブックのグラフィックスは，カーネルグラフィックスプリミティブに適用されたMakeBoxesのタイプセット規則の結果である．MakeBoxesは通常カーネルグラフィックスの構造を維持する．

• グラフィックスはWolframシステムの中で評価することができる．デフォルトではカーネル表現へと評価されることが多いが，オーバーロードしているMakeExpressionにより追加の評価規則が適用されることもある．

• ノートブックではカスタムのプラットフォーム非依存のビットマップ画像形式が使われる．この形式はビットマップセルおよびグラフィックス出力のキャッシュで使われる．

• グラフィックスのアンチエイリアスがサポートされるシステムでは，フロントエンドは選択的にアンチエイリアスを使い，可能な限り最適な2Dグラフィックスの描画を実行する．3Dグラフィックスは環境設定(Preferences)ダイアログの設定により，一様にアンチエイリアスが使われる．

可視化

• バージョン6では，非数値を返す関数を含む警告メッセージはデフォルトでOffとなっている．そのメッセージとはPlot::plnr，ParametricPlot::pptr，ParametricPlot3D::pp3tr等である．

• 可視化関数は，ほとんどの場合GraphicsComplexオブジェクトを返す．

• GraphicsComplexは頂点ベースの構造なので，ListDensityPlot等の関数はバージョン5とは全く異なる動作を見せる．ArrayPlot，ReliefPlot等の関数を使うと，バージョン5の ListDensityPlotと同様の結果を得ることができる．

• プロット関数には視覚的質を特に重視したさまざまな最新の幾何学的アルゴリズムが含まれる．

• Manipulate構造では，質を犠牲にしてプロットプロセスを高速化しようとする特殊なコードがデフォルトで使われる．PerformanceGoal，PlotPoints，MaxRecursion等のオプションでは最適化プロセスの完全な制御ができる．

• 除外では高度な記号的処理が使われる．Exclusionsオプションのあるプロット関数を初めて使うときに，システムにより除外パッケージがロードされるためわずかな遅延が生じる．

• 除外機能は，点および曲線付近の数値的オフセットを使用してジャンプや特異点を扱う．場合によっては，好ましくないギャップが生じることがある．それを回避するためにはExclusions->Noneを使う．

• PlotやParametricPlotでのように，曲線にColorFunctionを使うと，各線分に対して別々の色指示子が生成されるため，非常に大きい式が生成されることがある．

• 適応的調整は，純粋に幾何学的属性に基づいている．ColorFunctionの指定された曲線では，色の推移を滑らかにするためにPlotPointsの数を増やす必要がある可能性がある．

• MeshFunctionsでは符号のチェックにより切り捨て値を決定するために数値メソッドが使われているため，AbsやBooleのような関数は，メッシュの構築を実行するために使うことはできない．

• メッシュ線および等高線はオーバーレイではなく，その形状に不可欠な部分である．その結果，多数のメッシュ線または等高線により対応するGraphicsComplexで多数の多角形が生成される．

• Plot，ParametricPlot，Plot3D，ParametricPlot3D等の関数を使った関数可視化では，関数のTableはベクトルとして解釈される．したがって，すべての曲線および曲面に対するスタイルは同じである．表を個別の関数として明示的に拡張するためにはEvaluateを使う．

• ContourPlotでは，主な機能を決定するためにまずMaxRecursionが適用され，等高線を滑らかにするために2回目の再帰が使われる．MaxRecursion->n の値は 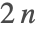レベルの再帰まで生成できる．

• ContourPlot3Dはすべての特異点を決定するために代数的関数を見付け，記号的解析を実行することができる．場合によっては，MaxRecursionのデフォルト値では特異点の詳細すべてを解決するのに十分でないことがある．そのような場合はMaxRecursionを大きくする．

• ContourLabelsはラベル間の最短距離を最大にするように置く．テキストスタイルとテキストサイズは最適な位置を決定する場合に考慮されない．

• 不規則データでは，ListPlot3Dはドローニ三角分割を構築する．大きい座標値では，いくつかの点が除去されることがある．データを再スケールすると結果が向上する．

• ListSurfacePlot3Dはデータにできるだけ近い曲面を見付けようとする再構築関数である．サンプル値の数が少ない領域では，曲面に穴が開く．

• ListSurfacePlot3Dのデータ点は，ゼロレベル曲面を見付けるために使われる距離関数を構築するために使われる．もとの点は最終的な結果の一部にならない．

フロントエンド

• フロントエンドはカーネルとの対話および内部での異なる要素間の対話にWSTPを使用する．

• フロントエンド中のすべてのメニュー項目および他の関数はWolfram言語式で表されている．

• 設定および初期設定ファイルはWolfram言語形式を使用している．

• ドキュメントは Wolframシステムノートブックで執筆される．その後特別のWolframシステムプログラムで処理され，最終的なドキュメントノートブックやオンラインドキュメントWebサイトをはじめ，カラーシンタックス情報のデータベースや使用法メッセージ等のWolframシステムコンテンツが作成される．

• 評価が終了すると，フロントエンドはカーネルにクエリしてユーザ変数についてのカラーシンタックス情報を維持する．複数の評価が待っている場合，クエリはそれぞれの評価の後には行われない．クエリは常にキューの最後の評価の後で実行される．

• フロントエンドの組込みダイアログボックスのほとんどは，Wolframシステムノートブックとして実装される．

ノートブック

• ノートブックはWolfram言語式で表されている．

• ノートブックファイルWolfram言語のコメントの形式で，キャッシュされたアウトライン情報を付加的に含んでいる．この情報を使用することで，より効果的なランダムアクセスが可能となる．

• ノートブックは段階的保存されることにより，データの再書き込みやすでに書き込まれたデータの移動を必要な限り最小限にとめることが可能である．

• デフォルトでは，機種に依存しないダブルバッファリングが使用され，ウィンドウの内容が更新されるときの画面のチラツキを最小にする．

• 自動スクロールは，コントロール理論機構を使用して，滑らかさと制御可能性を最適化する．

• すべての記号は内部的にもファイルでもUnicodeを使って表される．システムインターフェースおよび他のエンコードを使用するサードパーティーソフトウェアとの通信をサポートするために，多数のエンコードに対するマッピング表が含まれている．

• テキストをクリップボードにコピーするとき，技術的記号の多くとすべてのぷ来ベーススペース記号はUnicodeではなくその長い名前を使ってエンコードされる．これにより，それらの記号が適切に描画できないかもしれないソフトウェアにより可読性を向上させる．アルファベット記号はすべてシステムのローカル言語にかかわらずUnicodeでエンコードされる．

• スペルチェックは，標準英語，技術用語，Wolframシステムで使用される単語を含む10万語の英語辞書，およびアルゴリズムを使って実行される．スペル訂正は原文，表音韻律，キーボード距離法を使用している．

• ハイフン付けはLiangハイフン付けアルゴリズムと，英語ハイフン付けに対する標準TeXパターンを使って実行される．

動的評価

• フロントエンドは，通信するそれぞれのカーネルと3つの一意のリンクを構築する．1つはユーザにより開始された通常の評価のために使われるリンクであり，残りの2つはDynamicオブジェクトの値の更新に使われるものである．

• フロントエンドでDynamicオブジェクトがフォーマットされるとき，評価がカーネルに送られる．カーネルはDynamic評価で使用される変数をすべて依存表に記録する．

• カーネルの変数が変化すると，カーネルはフロントエンドにメッセージを送り，その変数に依存するDynamicオブジェクトを無効にする．その後依存表から依存情報を削除する．

• フロントエンドには，フロントエンドによってのみ決定することのできる値に依存するDynamicオブジェクトを追跡する依存表がある．これにはMousePosition，ControllerState，フロントエンドオブジェクトを調べるCurrentValue式に依存するDynamicオブジェクトが含まれる．

• フロントエンドがノートブックウィンドウを更新するためにカーネルにオブジェクトを送る場合，無効となったDynamicオブジェクトだけを送る．たとえば，スクリーン外にスクロールされたり別のウィンドウで隠されたりしたDynamicオブジェクトは更新されない．

• フロントエンドはすべてのDynamic評価で，評価をカーネルに送る必要があるわけではない．フロントエンドは，フロントエンド内のミニ評価体で計算できるほど小さいものかどうかを自動的に判断する．

• 通常の評価中にDynamic評価が生じた場合，カーネルは通常の評価を一旦中止し，Dynamic評価を処理する．カーネル評価を休止するメカニズムは，カーネルの中断やサブセッションでの評価に使われるものと同じである．

• フロントエンドはカーネルに送られる動的評価をTimeConstrainedでラップする．タイムアウトはDynamicEvaluationTimeoutオプションの値に設定される．また，フロントエンドは必要に応じてコンストラクト内の動的評価もラップし，DynamicModule変数を解決する．

WSTP

• Wolfram Symbolic Transfer Protocol (WSTP)はプレゼンテーションレベルでのプロトコルであり，メッセージおよびストリームに基づいているすべてのトランスポートメディアの上方に重ねることが可能である．

• WSTPはリンク両端が互いに互換なコンピュータシステムであると判断された場合はデータを圧縮したフォーマットでコード化する．

• WSTPはWolfram言語式と同様に割込みのようなバンド以外のデータでも転送可能である．

• 可能な限りWSTPは動的にリンクされる共有ライブラリを使用して実装されている．

式のフォーマット

• フロントエンドはフォーマットされた式のボックス構造を表すため指定された非循環グラフを使用する．

• ボックスは演算子優先パーサーの二次元への一般化を使用して解釈される．

• グラフィックスとタイプセットは，同じフォーマット言語で実装されているので，両者をシームレスに操作することができる．

• 段階的パーシングが構造およびディスプレイ更新を少なくするために使用されている．

• 文字間隔と位置決めはフォントデータと演算表から決定される．

• 改行はすべての式でTeXのテキストレイアウトに使用されているのと同様な方法で，大域的に最適化されている．

• 入力中，改行は式での小さな変化が大規模な再フォーマットを起すことは稀なようになっていて，入力がジャンプする場合は，楕円形のカーソル追跡子が瞬間的に現れ，視線を誘導する．

• 非常に長い出力の省略は，その出力のボックス表現のバイト数に基づく．グラフィックス等を表すために使われるボックス等，バイト数から除外されるボックスもある．

• 式のフォーマットには数千ページのC++コードを使用している．