关于内部实现的一些注释
举例来说，注释仅简单的说 DSolve 使用Kovacic 算法求解二阶线性微分方程. 但是用于实现这一功能的内部代码却有60多页长，包含了大量其它算法和大量精妙的思想.
表达式中元素的连续存放减少了内存的分块和交换. 但是，当一个长表达式中一个单独的元素被修改时，这可能导致对指针数组全部复制. 为了避免这种复制，Wolfram 语言使用了许多基于调用次数和预分配的优化技术.
在适当的场合，大的数列和嵌套数列自动以机器整数或实数的打包数组存放. Wolfram 语言译器自动被用来编译将要重复用到这种打包数组上的复杂函数. Wolfram Symbolic Transfer Protocol (WSTP)、DumpSave 及各种 Import 和 Export 格式在外部使用打包数组.
当大量的定义用于描述一特定符号时，会自动使用 Dispatch 格式生成一个哈希表，以便能迅速找到合适的法则.
数的表示和数值计算
- IntegerDigits、RealDigits 和相关的进制转换函数使用的是递归分治算法. 相似的算法用于数的输入和输出.
- N 使用一个自适应过程来提高它内部工作精确度以便达到所要求的任意一种总体精确度.
基本算法
伪随机数
- 对于 RandomReal 和 RandomInteger 等函数，默认的伪随机数生成器使用一种基于元细胞自动操作的算法.
数论函数
- GCD 使用HGCD 算法、Jebelean–Sorenson–WebG 加速 GCD 算法，加上一个由 Euclid 算法与一个基于 2 的幂循环排除算法组合而成的算法.
- PrimeQ 首先使用小素数检测整除性，然后使用 Miller–Rabin 强伪素数检测 2 进制和 3 进制，最后使用一个 Lucas 测试检测.
- Primality Proving Package 包中包含了一个较慢的算法，该算法被证明对所有的
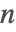都是正确的. 它能对是否是素数返回一个明确认证.
- FactorInteger 在试除法、Pollard
、Pollard rho、椭圆曲线和二次筛算法之间切换.
- Prime 和 PrimePi 使用稀疏缓存和筛选. 对于较大的
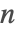， PrimePi 使用的是基于素数密度的渐进估计的 Lagarias Miller Odlyzko 算法，并被转换给出 Prime.
- LatticeReduce 使用的是 Lenstra–Lenstra–Lovasz 网格缩减算法的 Storjohann 变形.
- 为了找到所要求的一定数目的项， ContinuedFraction 使用修正Lehmer间接法，并通过一种自动重启的分治算法来降低每一步所必需的数值精确度.
- ContinuedFraction 利用递推关系为二次无理数寻找循环连分数.
- FromContinuedFraction 使用由分而治之法优化的迭代矩阵乘法.
复合函数
- Binomial 及其相关函数使用一个分治算法来平衡中间乘积的位数.
- Fibonacci[n] 使用基于
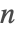的二进制序列的迭代方法.
- 对于较小的
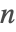，PartitionsP[n] 使用 Euler 五边形公式，而对较大 
，则使用非递归的 Hardy–Ramanujan–Rademacher 方法.
- ClebschGordan 及其相关函数使用广义超几何级数.
初等超越函数
数学常数
- Pi 使用 Chudnovsky 公式计算.
- E 通过它的级数展开进行计算.
- EulerGamma 使用的是 Brent–McMillan 算法.
- Catalan 通过广义超几何和进行计算.
特殊函数
- Gamma 使用递归、函数方程和 Binet 渐进公式.
- PolyGamma 使用 Euler-Maclaurin 和式、函数方程和递归.
- PolyLog 使用 Euler-Maclaurin 和式、不完全gamma函数的展开、数值积分和 Hurwitz zeta 函数的一种函数方程.
- Zeta 及其相关函数使用 Euler-Maclaurin 和式以及函数方程. 在临界区附近也使用 Riemann Siegel 公式.
- StieltjesGamma 使用用 Keiper 算法，该算法基于一个zeta函数的积分表示的数值积分和使用 Bernoulli 数进行交错级数求和.
- 超几何函数使用函数方程、稳定的递推关系、级数展开、渐进级数和帕德逼近式. 有时也使用 NSum 和 NIntegrate 的方法.
- ProductLog 使用始于有理近似和渐进展开的高阶 Newton 法.
数值积分
- NIntegrate 使用符号预处理来解决函数对称性问题，将分段函数扩展至各情形，将由不等式设定的区域分解为单元.
- 当 Method->Automatic 时，NIntegrate 在一维情形下使用 "GaussKronrod"，而在其它的情形下使用 "MultiDimensional".
- 如果直接给出了 MaxPoints 的设置，NIntegrate 缺省使用 Method->"QuasiMonteCarlo".
数值的和与乘积
- 否则使用 Integrate 或 NIntegrate 的 Euler–Maclaurin 求和.
数值微分方程
- 对于普通的微分方程，NDSolve 默认使用一种 LSODA 方法，在非刚性Adams方法与刚性Gear反向微分方法之间切换.
- NDSolve 及其相关函数的代码的代码约有1400页.
近似方程求解和优化
- 对代数方程组，NSolve 首先使用一个有效的单项式排序计算出一个数值的 Grobner 基，然后使用特征值方法来确定根的数值解.
- FindRoot 使用了减幅 Newton 法，正割法和 Brent 方法.
- 通过 Method->Automatic 的设置和两个初始值，FindMinimum 使用 Brent 的主轴方法. 通过对每个变量赋以一初始值，FindMinimum 使用 BFGS 形式的拟 Newton 法，对于大型的系统具有有限的内存变体.
- 如果极小化函数是一个平方式的和，FindMinimum 使用 Levenberg–Marquardt方法(Method->"LevenbergMarquardt").
- FindMinimum 在有约束时，使用内点法.
- LinearProgramming 使用单纯形法和修正单纯形法，且当 Method->"InteriorPoint" 时，使用原有对偶内点法.
- 对于线性情形，NMinimize 和 NMaximize 使用与 LinearProgramming 相同的方法. 对于非线性情形，尤其是当出现整数变量时，则使用 Nelder–Mead 方法，辅以差分演化.
- LeastSquares 使用 LAPACK 的最小二乘函数.
数据处理
- Fourier 使用结合长度素因子分解的FFT算法. 当素数因子很大时，则使用快速卷积方法来保持
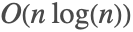的渐进复杂度.
- 对于实数输入，Fourier 使用一个实变换方法.
- ListConvolve 和 ListCorrelate 尽可能使用 FFT 算法. 对于准确的整数输入，则使用二元分割将问题简化为大整数乘法.
- InterpolatingFunction 使用均差来构造 Lagrange 或者 Hermite 插值多项式.
- Fit 使用的是奇异值分解. FindFit 对于线性最小二乘情形使用相同的方法，对于非线性最小二乘情形使用 Levenberg–Marquardt 方法，其它时候使用一般的 FindMinimum 方法.
- CellularAutomaton 通常使用数元截割的位包装并行运作. 对于基本规则，并行操作使用的是最优布尔函数，而对于许多极权规则，使用的是适时编译位包装表. 在二维时，对于运行于 Moore 邻域和无限背景状态时的双色静态规则，则尽可能使用稀疏位包装数组，只更新激活状态的集群.
近似数值线性代数
- 涉及到模式规则的 SparseArray 使用柱形代数分解来找到连接的数组元件. 稀疏矩阵使用压缩稀疏行格式被内部存储，被推广至张量任意秩.
- LUDecomposition、Inverse、RowReduce 和 Det 使用带部分主元消元的的 Gaussian 消去法. LinearSolve 使用相同的方法，并结合高精度数的迭代改进.
- 对于稀疏矩阵，LinearSolve 使用 UMFPACK 多面直接求解法， 当 Method->"Krylov" 时使用 Krylov 迭代法，并且由一个不完整的LU分解预处理. 对于高精度数，它使用自适应迭代改进法. Eigenvalues 和 Eigenvectors 使用 ARPACK Arnoldi 方法.
- SingularValueDecomposition 使用带 Givens 变换的 QR 算法. PseudoInverse、NullSpace 和 MatrixRank 基于 SingularValueDecomposition. 对于稀疏矩阵，使用的是 Arnoldi 方法.
- QRDecomposition 使用 Householder 变换.
- SchurDecomposition 使用 QR 迭代.
- MatrixExp 使用变量序的帕德逼近，使用 Paterson–Stockmeyer 或 Krylov 子空间近似方法进行有理矩阵函数的计算.
准确数值线性代数
- Inverse 和 LinearSolve 使用基于数值近似的有效行变换法.
- 当 Modulus->n 时，则使用模 Gaussian 消元法.
- Det 使用模方法和行变换，通过使用中国剰余定理构造出结果.
- Eigenvalues 通过对特征多项式进行插值来实现.
- MatrixExp 使用 Putzer 方法或者 Jordan 分解.
多项式处理
- 对于单变量多项式，Factor 使用一种 Cantor–Zassenhaus 算法的变形按模分解一个素数，然后使用Hensel上升重组法在整数域构造因子.
- 对多变量多项式，Factor 通过用适当的整数选择替换除一个变量外的所有变量，然后分解所得到的单变量多项式，并使用 Wang 的算法重新构造多元因数来实现.
- 除一般多项式处理外的 Factor 的内部代码约有250页.
- FactorSquareFree 通过寻找一个导数然后反复计算GCD来实现.
- Resultant 要么使用显式子结式多项式剩余序列要么使用附有中国剰余定理的模序列.
- Apart 要么使用帕德技术要么使用待定系数法.
- PolynomialGCD 和 Together 通常使用包括 Zippel 稀疏模算法在内的模算法，但在某些情况下使用子结式多项式剩余序列.
符号线性代数
- RowReduce、LinearSolve、NullSpace 和 MatrixRank 都基于高斯消元法.
- Inverse 使用了余子式展开和行变换. 主元通过寻找简单表达形式来选取.
- 对小矩阵，Det 直接使用余子式展开，而对较大的矩阵则使用高斯消元法.
- MatrixExp 首先找到特征值然后使用 Putzer 方法.
准确方程求解与化简
- 表示代数数的 Root 对象常常使用有效的数值方法来分隔开和处理. 当 ExactRootIsolation->True 时，对于实根，Root使用基于 Descartes 符号法则的一个算法的连分式，而对于复根则使用 Collins-Krandick 算法.
- 对多项式方程组， Solve 构造一个 Gröbner 基.
- Solve 和 GroebnerBasis 使用一种有效的 Buchberger 算法.
- 对非多项式方程， Solve 试图改变变量并增加多项式条件.
- Solve 及其相关函数的代码约有500页.
- 对于多项式方程组，在实数域上 Reduce 使用柱形代数分解，在复数域上使用 Gröbner 基的方法.
- 对于代数函数，Reduce 构造等价的纯粹多项式系统. 对于超越函数，Reduce 产生由超越条件组成的多项式方程组，然后使用函数关系和逆图像信息数据库将其化简. 对于分段函数，Reduce 进行符号式扩展来构造一个连续方程组的集合.
- 对于单变量超越方程，Reduce 用超越 Root 对象来表示解集. 对于实数域上的指对数函数方程，Reduce 使用一种准确的指对数根隔离算法. 对于有界实数或复数域上的解析函数方程，Reduce 使用有效数值方法. 对于初等函数，根的数量和位置都采用区间算术方法被充分验证. 对于非初等函数，根的数量的验证取决于数值积分的正确性，根的位置的验证取决于由 Wolfram 语言的有效算术所提供的准确性估计的正确性.
- CylindricalDecomposition 使用 Collins–Hong 算法并对导向性良好的集合结合使用 Brown–McCallum 投影，对其它集合结合使用 Hong 投影. CAD 的构造是通过 Strzebonski 的基于系统学的方法，使用由准确代数数计算支持的验证后的数字. 对于0维方程组则使用 Gröbner 基的方法.
- GenericCylindricalDecomposition 使用一种 CAD 算法的简化版本，它使用的是较简单的投影算符，并且只构造有理数采样点的单元.
- 对于丢番图方程组，Reduce 使用 Hermite 正规形式对线性方程进行求解，使用 Contejean–Devie 方法对线性不等式进行求解. 对于单变量多项式方程，它使用一种改良的 Cucker–Koiran–Smale 方法，而对于二元二次方程，对于椭圆，它使用 Hardy–Muskat–Williams 方法，对于 Pell 及其它情形它使用经典的技术.Reduce 囊括了用于大约25个丢番图方程类别的专门方法，包括用于 Thue 方程的Tzanakis–de Weger 算法.
- 对于素数模量，Reduce 对线性方程采用线性代数，对于多项式方程在素数域上采用 Gröbner 基. 对于复数模量，则在整数域上使用 Hermite 正规形式和 Gröbner 基.
- Reduce 及其相关函数使用大约350页的 Wolfram 语言代码以及1400页C代码.
准确优化
化简
- FullSimplify 自动使用约40种一般代数变换以及大约400种特殊数学函数的法则.
- FunctionExpand 使用广义高斯算法来展开含有
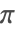的有理数倍参数的三角函数.
- Simplify 和 FullSimplify 在适当的时候对结果进行缓存.
- 如果指定变量是实数，多项式的约束使用柱代数分解的方法来处理，而线性约束由单纯形算法或 Loos–Weispfenning 线性量词消去法处理. 对于严格的多项式不等式，则使用 Strzebonski 的通用 CAD 算法.
微分和积分
- 许多其它的定积分使用了 Marichev-Adamchik Mellin 变换方法来实现. 其结果最初常常表示由 Meijer G 函数表出，从而可以使用 Slater 定理转换为超几何函数然后进行化简.
- Integrate 使用了约500页 Wolfram 语言代码和600页C代码.
微分方程
- DSolve 使用了约300页 Wolfram 语言代码和200页C代码.
和与乘积
级数和极限
- Series 通过递归对带参数级数展开的函数进行级数展开实现.
递归方程
- RSolve 使用矩阵幂来求解常系数线性方程组.
图形
- 三维渲染程序采用两种不同的方法多边形排序. 对于不包括透明度的图形场景，使用一种硬件加速深度缓冲器. 否则，渲染程序使用二进制空间分割树从任何角度进行多边形的分裂和排序. BSP 树的创建较慢，并且不是硬件加速，但它提供了支持多边形的最一般的能力.
- 图形可以被 Wolfram 语言计算. 默认情况下，它们通常会计算其内核表示，尽管其它计算规则可能通过超载 MakeExpression 来实现.
- 对于支持图形反锯齿的系统，前端选择性地使用反锯齿，以确保二维图形的最佳渲染. 三维图形根据 Preferences 对话框的设置均匀的反锯齿.
可视化
- 在第6版中，涉及返回非数字值的函数的警告信息在默认情况下为 Off. 这些信息包括 Plot::plnr, ParametricPlot::pptr 和 ParametricPlot3D::pp3tr.
- 可视化函数在大多数情况下返回 GraphicsComplex 对象.
- 由于 GraphicsComplex 是一个基于顶点的构建，诸如 ListDensityPlot 的函数的行为与在第5版中完全不同. ArrayPlot 和 ReliefPlot 等函数可得到与第5版中的 ListDensityPlot 相似的结果.
- 试图通过牺牲绘图质量使绘图进程加快的特殊代码在 Manipulate 的构造中默认使用. 诸如 PerformanceGoal、PlotPoints 和 MaxRecursion 等选项允许完全控制优化过程.
- 排除选项利用了高度精密的符号处理. 当带有 Exclusions 选项的绘图函数首次使用时，系统需要加载排除包，这会导致轻微的延迟.
- 排除功能通过点和曲线周围的数值抵消来处理跳跃和奇点. 在某些情况下可能会出现不想要的差距. 使用 Exclusions->None 可以避免这种缺陷.
- 当 ColorFunction 被用于曲线时（例如在 Plot 和 ParametricPlot 中），非常大的表达式可以创造，因为每一段都生成一个单独的颜色指令，可能会创建非常大的表达式.
- 自适应细化纯粹基于几何性质. 对于具有 ColorFunction 的曲线，可能需要增加 PlotPoints 数量得到平滑的色彩过渡.
- MeshFunctions 使用数值方法通过检查运算符号来确定切削值，所以像 Abs 和 Boole 函数不能被用来推动网格的构造.
- 网格线或轮廓线是几何图形的一个组成部分，而不是覆盖层. 因此，大量的网格线或轮廓线将产生大量相应于 GraphicsComplex 的多边形.
- 在使用诸如 Plot、ParametricPlot、Plot3D 和ParametricPlot3D 等函数进行的函数可视化中，一个函数 Table 被解释为向量. 因此，对于所有曲线或曲面，其风格将是相同的. 使用 Evaluate 强制扩展独立函数的表格.
- 在 ContourPlot中，首先应用 MaxRecursion 的值确定主要特征，然后使用第二递归阶段理顺轮廓曲线. 请注意的是， MaxRecursion->n 的值可能产生高达
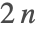个递归层.
- ContourPlot3D 可以识别代数函数并执行一个符号分析，以确定所有的奇点. 在某些情况下， MaxRecursion 的默认值可能不足以解决所有沿奇点的细节. 在这种情况下要增大 MaxRecursion.
- ContourLabels 以使标签之间的最小距离最大化的方式放置. 文字风格和文字大小在确定最佳位置时不予考虑.
- 对于不规则的数据， ListPlot3D 构造一个 Delaunay 三角. 对于大型的坐标值，可能会放弃一些点. 缩放的数据将改善结果.
- ListSurfacePlot3D 是一个重建的函数，它试图找到一个尽可能接近数据的表面. 采样值低的区域将导致表面上有洞的出现.
- ListSurfacePlot3D 中的数据点用于构造寻找零级表面的距离函数. 原始点并不是最终结果的一部分.
前端
笔记本
- 当复制文本到剪贴板时，许多技术特点和所有私用空间字符都使用详细的的长名字编码，而不是利用其 Unicode 值，以改善软件对这些字符的可读性，因为这些字符可能无法通过这些软件正确呈现. 所有字母字符都以 Unicode 的形式编码，与系统的本地化语言无关.
动态计算
- 前端与与之通信的每个内核建立3个独特的链接. 一个链接用于由用户发起的定期计算，而其他两个链接用于更新 Dynamic 对象的值.
- 当内核中的变量发生变化时，内核向前端发出信息使任何依存于该变量的 Dynamic 对象失效，然后从附属表中去除该依存关系的信息.
- 前端有一个依存关系表用于跟踪 Dynamic 对象，这些对象所依靠的值只能由前端确定. 这包括依靠 MousePosition、ControllerState 或任何探测前端对象的 CurrentValue 表达式的 Dynamic 对象.
- 不是所有的 Dynamic 计算都被前端发送至内核. 前端自动确定一个计算是否只需通过前端内的小型计算器完成.
- 前端把在 TimeConstrained 中发送给内核的动态计算包装，并将超时设置为 DynamicEvaluationTimeout 选项的值. 前端还在构造中包装动态计算，以便必要时求解 DynamicModule 变量.