式のテキスト形入出力

入出力の表記法Wolfram言語の文法
入出力の働き演算機能が未定義の演算子
式の拡張テキスト形式出力書式の定義
テキスト記述の式の解釈低レベル入出力の規則
式のアウトライン表示構造化されていない式の出力
書式付きテキスト表示フォーマット出力
数値の出力書式Wolfram言語のGrid，Row，Column
表と行列ユーザからの入力
出力におけるスタイルとフォントメッセージ
ボックス形テキスト表記メッセージ：英語以外の言語への対応
ボックスの文字列表記説明文
文字列，ボックス，式の間の変換
入出力の表記法
　
式を標準的な記述形式で入力する：
同じ式をカーネル内部の表現に準じた記述形式で入力する：
ノートブックに入力する場合は，数学表記的な記述形式で入力することも可能である：
出力式に関しても用途に応じて表記法を選択することができる．
Wolframシステムノートブックでは，StandardForm（標準形）と呼ばれる，より数学表記的な記述形式で答が出力される：
OutputForm（出力形）を作用させ，キーボードの文字だけを使う記述形式で答を表示する．Wolfram言語のテキスト型インターフェースではこの形式が通常使われる：
キーボードから直接入力できる文字，記号だけを使う．InputForm（入力形）を作用させると，答を再入力可能な記述形式に変換できる：
FullForm（完全形）を使いカーネル内部で使われる関数形の記述形式で表示する：
FullForm[expr]
式の記述をカーネルの内部表記に変換する
InputForm[expr]
キーボードの文字と記号だけで構成される入力式の記述形式に変換する
OutputForm[expr]
キーボードの文字と記号だけで構成される出力式の記述形式に変換する
StandardForm[expr]
Wolframシステムノートブックの標準記述形式に変換する
出力式の表記変換
カーネルから式の出力があるとき，上記の出力表記のいずれかに基づいたテキスト形式で式が構成される．テキスト形式の式は，内容によっては，再度入力式として使うことも可能である．上記の表記の他にさらにいくつかの表記と変換機能が用意されている．それらは主にタイプセット的な表示，もしくは，外部プログラムへの出力用途で使う．
TraditionalForm（慣用形）を使い答を慣用的な数学表記で表示する：
TeXFormを作用させTeX形式に変換する：
MathMLFormは出力をMathMLで与える：
CFormを使いC言語の記述形式に変換する．Powerはマクロのことで，その定義はファイルmdefs.hにある：
FortranFormを使えば，Fortran言語の記述形式にも変換することができる：
TraditionalForm[expr]
慣用形へ変換
TeXForm[expr]
TeX形式へ変換
MathMLForm[expr]
Web上で使われるMathML形式へ変換
CForm[expr]
C言語形式へ変換
FortranForm[expr]
Fortran形式へ変換
通常は再入力が不可な出力表記への変換
上記以外の特殊な出力表記が必要ならば，カスタマイズすることも可能である（詳しくは，「低レベル入出力の規則」を参照のこと）．ただし，外部プログラムへ式を送る場合は，可能であれば，Wolfram Symbolic Transfer Protocol (WSTP)を使い直接転送した方がよい．
■ 式を特定テキスト形式に変換してから外部プログラムに読み込ませる．
■ WSTPを介して式を直接転送する．
外部プログラムにおけるWolframシステムで作成した式の転送法
入出力の働き
Input
テキスト形式の記述文を式に変換する
計算
式を計算する
Output
評価結果としての式をテキスト形式に変換する
Wolfram言語の基本処理ステップ
ユーザがx^2と入力したなら，まず，文字列(x, ^, 2)の認識作業がカーネルにおいて行われる．カーネルの環境設定が標準通りになっているなら，文字列から式Power[x,2]への変換が速やかに行われる．
そして，可能な処理が全部済んだら，Wolfram言語は式Power[x,2]を取り，それを出力のためのテキスト形式の表現に変換する．
入力式がx, ^, 2の文字列に分解・検査され，式Power[x,2]に変換される：
Fortran形式で式を再表示する：
FortranFormは「包み込み」演算子であり，Out[2]の答はPower[x,2]のままである：
In[n]とOut[n]のセルに記録されるのは実際に評価処理された内部形式の式で，必ずしも，最終的な表示に現れる記述式ではないことに注意する．
例えばTraditionalForm[expr]を使い，特別な種類の出力を明示的に要求すると，出力セルにはOut[n]//TraditionalFormのラベルが付く．これは，表示される式は expr//TraditionalFormであるが，Out[n]セルの内容としてはもとの式 expr のままであるということを意味している．
特定の式だけでなく大域的に出力表記法を指定することも可能である．その場合，表記名はセル番号の脇に表示されない．大域的に指定しても，In[n]とOut[n]のセルが持つ内容は基本的なテキスト形入出力式の記述のままでおかれる．
FortranFormを作用させた右辺をtに割り付ける：
実際にセルに取り込まれたのはWolfram言語標準形の式である：
ただし，tを参照するとFortranFormの機能が有効なので，FortranFormで式が返ってくる：
tに演算操作をすると，答の式がFortranFormで表示される：
式の拡張テキスト形式
式のテキスト形式は，Wolframシステムの他の要素と同様に式として表現することができる．一次元の文字列から構成されるテキスト形式は，通常のWolframシステム文字列として直接表すことができる．しかし，添字（下付き文字）や指数（上付き文字）等の縦横に広がる二次元的な表示を想定した数学記号（2D記号）は標準テキスト形式では記述できない．代りにボックスオブジェクトと呼ばれる記述単位を使った拡張テキストを使う．
一次元文字列
InputForm
，
FullForm
等
二次元ボックス
StandardForm
，
TraditionalForm
等
式のテキスト記述法
InputForm（入力形）で式を記述した後，文字列に変換する：
FullForm（完全形）を作用させると，文字列であることが分かる：
文字列だから文字成分に分解することも可能である：
StandardForm（標準形）で式を記述した後，ボックス形式に変換する：
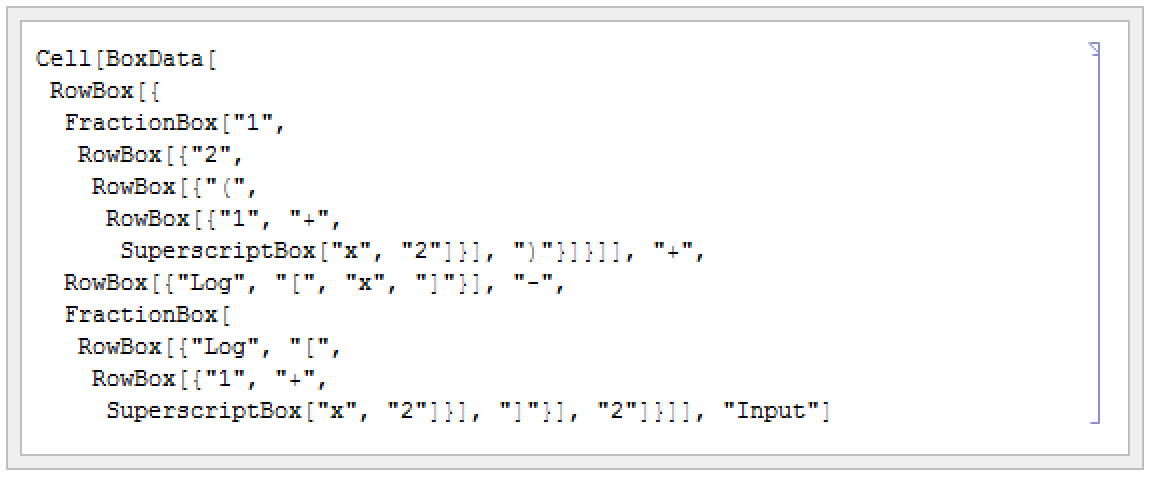
ボックス記述をInputFormに変換してみる．この表記では，各成分は文字列として表示される：
ノートブック用フロントエンドを使っている場合は，メニューからセルを式で表示のコマンドを選択すると式の表示内容をテキスト形式で見ることができる．
StandardFormの記述式を持つセルの例：

1.gif

セルを式で表示を使い，この式をボックス形式で表示すると，式の構成が明確になる：

2.gif

ToString[expr,form]
テキスト形式で記述した式 expr を文字列に変換する
ToBoxes[expr,form]
テキスト形式で記述した式 expr をボックス形式に変換する
式の文字列変換とボックス変換
テキスト記述の式の解釈
ToExpression[input]
文字列やボックスを解釈し式に変換する
文字列とボックスの式への変換
文字列を式に変換する：
StandardFormの式をボックス形式に変換する：
ToExpressionはボックス形式を解釈し，もとの式を再構築する：
式はテキストとして入力される．入力があると，実行的なToExpressionの機能が効果的に使われ，テキストが評価可能な式を表しているかどうかを解釈する．
ノートブック用フロントエンドを使っている場合，入力したセルの内容が評価のためカーネルに送られるものに限って上記の解釈作業が行われる．したがって，ノートブックで数式等を書くとき，それがカーネルに送られるものでなければ，特にカーネルの認識可能な形式でなければいけないということはない．
FullForm
明示的な関数の記述形式
InputForm
一次元的な行モードの記述形式
StandardForm
二次元的な数学記号を直接表示編集可能にする記述形式
入力式の表記法と階層関係
同じ式を表記別に入力する．まず，FullFormで行う：
次にInputFormで入力する：
最後に，StandardFormで入力する：
Wolframシステムには入力テキストと式の対応関係を定義した変換規則が組み込まれている．ToExpressionを使うと，その変換規則をもとに入力テキストから式への変換が行われる．
これらの変換規則が集まりWolframシステム言語の文法を形作っている．変換規則の例として，x+y とタイプすると関数形の式Plus[x,y]が生成されるとか，xy と入力すると式Power[x,y]が生成される等がある．FullFormの入力であれば解釈に使う規則は単純明快である．つまり，「式は必ず特定頭部を持ち，頭部の後には角カッコでくくった引数要素が続く」とする．入力形式がInputFormになると規則はやや複雑になる．演算子の+や，関係記号である=や->を許容しながら被演算子（オペランド）を適切に読み取らなければいけない．StandardFormにおいては一層複雑な規則が必要になる．対処しなければいけない演算子や被演算子は単純な一次元配置のものだけでなく，分数や積分記号に見られるような二次元的な広がりを持つものもある．
以上3つの表記法FullForm，InputForm，StandardFormは階層的な関係でつながっている．つまり，FullFormで記述可能なものはInputFormですべて有効であるし，InputFormで有効なものはStandardFormでも有効である．
ノートブック用フロントエンドを使っているなら，StandardFormの提供するすべての機能を利用したい．使うフロントエンドがテキスト型インターフェースなら，普通はInputFormを使うしかない．
ノートブックでStandardFormを使っている場合，x2や注釈付きのグラフィックス等の数式を直接入力し，また，編集することができる（数学記号は左右だけでなく上下等にも広がりを持つので二次元的な記述になる）．しかしInputFormでは，一次元形式しか使えない．
評価しないでその解釈形が決められるStandardForm式をコピーすると，外部アプリケーションにはInputFormとしてペーストされる．それ以外の場合は，テキストは∖!∖(…∖)を使った二次元構造を正確に表す線形形式でコピーされる．この線形形式をWolframシステムノートブックに再び打ち込んだ場合，自動的に二次元形式に変換される．
ToExpression[input,form]
入力文 input がテキスト形式の表記で与えられたと仮定して式を生成する
他のテキスト形式からの変換
テキスト形式を使い，StandardFormとそのサブセットであるFullFormとInputFormのどれでも式を記述することができる．これらの表記法に基づいた記述文は1対1の関係で確実に式に変換することができる．
テキスト形式の記述法にはTraditionalFormと呼ばれるもう1つの記述法がある．TraditionalFormは主に出力用に使われ，Wolframシステムの認識する式なら何でも表示することができる．ただし，TraditionalFormの記述はStandardFormに比べ正確性に欠ける．また，一度，TraditionalFormで式を出力したら，その式からもとの式は再構築できないときもある．
それでも，書式ToExpression[input,TraditionalForm]を使えば，TraditionalFormの記述から強制的に式を生成させることは可能である．確実な解釈は保証されない．
文字列をTraditionalFormの式として認識させる：
同じ式の文字列をStandardFormにすると，違った解釈がなされる：
計算結果をTraditionalFormで生成した場合，式の各成分に対応したボックス記述には特殊なInterpretationオブジェクト，あるいは，TraditionalForm出力からどのように式を再構築するかを指定する特殊なタグの付いた形式が含まれる．
この拡張情報の埋め込み処理はStandardFormからTraditionalFormに変換した式に対しても行われる．ただし，はじめからTraditionalFormで式を編集したり，TraditionalFormの出力式に著しい変更を施した場合は，拡張情報が失われてしまい，式の正確な解釈が困難になってしまうので注意する．
式のアウトライン表示
計算をさせ非常に長い答が返ってくるとき，答のすべてを見たくないときもあるだろう．全体の形がどうなっているか知りたいかもしれない．そして式の形が分かったならば部分的に詳細がどうなっているか見てみたいこともある．
そのようなときは，関数ShortとShallowを使うと式を省略表示できる．
Short[expr]
式 expr の部分を1行分表示する
Short[expr,n]
式 expr の部分を n 行分表示する
Shallow[expr]
式 expr の木構造において最上位（最も浅いレベル）の部分だけを表示する
Shallow[expr,{depth,length}]
式 expr の木構造において指定レベルの深さと長さまで表示する
式のアウトライン表示
この計算結果は非常に長いものになる．実際に表示させたなら，23行程度続いてしまうだろう：
そこでtを短縮表示させる．答の中の<<>>とは省略された項の数を示す：
Wolfram言語によりOutputFormのようなテキスト形式の出力が生成される場合，まず，式が長くても短くても単一行で全部分が生成される．次に，表示行の幅を見て，それに収まるように式が複数行に分割される．このとき，各行には上付き文字や分数等の数学記号が入っていて実際の表示では1行分の高さ以上になることもある．なお，短縮表示関数Shortに指定できる行数は，出力装置に実際に表示される行の数ではなく「論理行数」であることに注意する．
tの答を4行分だけ表示する．先程より多くの項が見えるようになる：
ShortはStandardForm，TraditionalForm等の別の形式でも使える．これらの形式を使う場合は，改行は出力を生成するときにカーネルによって決められるのではなく，出力を表示するときにノートブックインターフェースにより決められる．その結果，Shortにより生成される線の数の設定は，スクリーンで表示される実際の線の数を近似するだけとなる．
Shortを別の出力表示の制御機能と組み合せて使ってもよい．ここではInputFormの変換関数と一緒に使う：
Shortの機能は，指定した行数になるまで出力式から部分を1つずつ除去する．場合によっては，出力する行数を制限するより，種類別に式の部分を制限した方が分かりやすい．その場合，上位部分だけを表示させるための書式，Shallow[expr,{depth,length}]が使える．この短縮機能を使うと，式の木構造における指定の深さ以下の部分を出力禁止にできる．長さ length は，出力に残しておく関数の引数最大数を指定する．
Shallowで違った式tのアウトラインが見られる：
今度は，表示する関数は何でもよいとし，引数を10個までに制限する：
特に，式がネストしているときは（Traceで得られる結果等で），Shallowを使うと式全体を通しで一様に整理でき便利である．
帰納的関数であるフィボナッチ(Fibonacci)の関数を定義する：
トレースしてみる．結果が長くなるので，表示は禁止にしておく：
Shallowを使い式のアウトラインを表示する：
Shortだと，あまり一様なアウトラインは得られず，式の形が分かりにくい：
ノートブックインターフェースで生成された出力がかなり大きい場合，Wolfram言語は自動的にその出力にShortを適用する．このように向上したユーザインターフェースにより，ユーザが期待していないような評価の出力を生成しフォーマットするのにWolfram言語が長時間掛けるのを防ぐことができる．
通常，このような割当ての最後にはセミコロンがある：
ユーザインターフェースのボタンにより，どれくらいの出力を見るかを制御することができる．この動作が有効となる大きさの閾値は，出力式のバイト数による．そのバイト数は，大きさ制限の設定ボタンで開くノートブックインターフェースの環境設定ダイアログで設定することができる．
書式付きテキスト表示
"text"
任意テキストからなる文字列の指定
文字列の指定
出力には引用符がないことに注目：
入力形にすれば引用符を見ることができる：
文字列にはどんな種類のテキストでも入力可能である．英語以外の文字でもよいし，改行記号や他の制御情報であってもよい．文字列の構成要素の詳細については「文字と文字列」を参照のこと．
StringForm["cccc``cccc",x1,x2,…]
第1引数の文字列において2重アクセント記号 `` があればそれを xi で順番に置換した文字列を構成する
StringForm["cccc`i`cccc",x1,x2,…]
第1引数の文字列においてパターン`i` があれば番号に対応した xi で置換した文字列を構成する
文字列の部分的置換
文字列を使うとき，場合によっては，原形になる文字列をテンプレートとして用意しておき，そこに種々の文字要素を挿入して必要な文字列を作成できると便利である．StringFormを使うとそれができる．
``の位置に第2，第3の引数を順番に挿入し新たな文字列を作る：
アクセント記号と数字を組み合せて，何番目の式を挿入すべきか指定することも可能である：
StringFormにおける引数の文字列は，C言語やFortran言語で使う書式付き出力文の「書式指定」に相当する．標準出力変換関数を式に作用させれば，StringFormの式がどう書式設定されるか見ることができる．
標準出力変換関数を使い，StringFormに指定した代入式に関し書式を指定する：
StringFormが使えるのは出力書式の指定だけであることに注意する．式自体の評価は行わない．StringFormオブジェクトから通常の文字列を生成するにはToStringの機能を使う．
StringFormが生成する書式付き出力には標準的な出力形が使われる：
入力形にすると，StringForm全体を1つのオブジェクトとして扱うことができる：
これはStringFormオブジェクトから通常の文字列を作成する：
StringFormを使えば，文字列で「テンプレート」を作り，そこに，いろいろな式を埋めていくという形式の入力ができる．場合によっては，複数の式がすでにあり，それらを単につなげたいだけのこともあるだろう．そのようなときは，Rowを使う．
Row[{expr1,expr2,…}]
連結した expri の出力形を返す
Row[list, s]
連続要素間に s を挿入する
Spacer[w]
Rowで使用することのできる w ポイントのスペースを生成する
Invisible[expr]
expr の物理次元により決められるスペースを生成する
式のシーケンスの出力
Rowは連結した式のシーケンスとして出力する：
Rowはタイプセット式でも使える：
Rowは表示された要素間にどのような式も自動的に挿入することができる：
Spacerは要素間の正確なスペースを制御するために使うことができる：
Column[{expr1,expr2,…}]
オブジェクトの左揃えの列
Column[list,alignment]
指定された横の整列での列 (Left, Center または Right)
Column[list, alignment, s]
s のx-heightで分けられた要素を持つ列
式の列出力
2つの式を上下に並べて表示する：
Defer[expr]
expr の評価を保留したままで expr の出力形を返す
Interpretation[e,expr]
e として表示されるが expr として評価される出力を返す
評価が保留された式の出力
テキスト文字列とRowのような関数を使うと，有効なWolfram言語式には必ずしも対応しない出力を生成することができる．しかし，式が評価されない限りにおいてのみ，有効なWolfram言語式に対応する出力が生成したい場合もあろう．関数Deferは引数の評価を保留するが，標準的なWolfram言語の出力形でフォーマットすることができる．
Deferは1+1の評価を保留する：
Deferは実際の割当が行われないようにする：
出力を変更したり，コピーペーストを使うことでDeferの出力が再び評価されると，通常通りに評価される．
下の出力は上記の出力セルから入力セルへとコピーしたものである：
Interpretationを使うと，評価方法とは直接関係しない外観を持つ出力を生成することもできる．最も解読可能な形式がオブジェクトの内部表現によく対応していないような出力をフォーマットするときに，この方法がWolframシステムで効率的に使われる．例えば，Seriesはデフォルトの出力で常にInterpretationオブジェクトを生成する．
下の出力はyと表示されるが，xとして評価される：
前の出力のコピーペーストにより，以前にxに割り当てられた値が参照される：
数値の出力書式
ScientificForm[expr]
数値を科学表記で表示する
EngineeringForm[expr]
数値を工学表記で表示する（指数部が3の整数倍の値になるように仮数部の小数点位置が調整される）
AccountingForm[expr]
数値を会計表記で表示する
数値の特殊表記
出力にはデフォルトの書式が使われる．数値が大きければ科学表記が使われる：
すべての数値を科学表記で表示する：
今度は，工学表記で表示する．指数部が3の整数倍になるように仮数部が調整される：
会計表記では，負の数値は丸カッコでくくられる．科学表記は全く使われない：
NumberForm[expr,tot]
式 expr にある近似実数を最長で tot 桁まで表示する
ScientificForm[expr,tot]
式 expr にある近似実数を最長で tot 桁まで科学表記で表示する
EngineeringForm[expr,tot]
式 expr にある近似実数を最長で tot 桁まで工学表記で表示する
実数表示精度の指定
の実数値を30桁精度で表示する：
今度は の10桁分だけ表示する：
12桁精度の工学表記で表示する：
オプション
デフォルト値
DigitBlockInfinity
コンマ等の区切り記号を挿入する桁の間隔を指定する
NumberSeparator{","," "}
小数点以上の位の桁と以下の位の間隔を区切る記号を指定する
NumberPoint"."
小数点を表す記号を指定する
NumberMultiplier"∖[Times]"
科学表記における乗算記号を指定する
NumberSigns{"-",""}
負と正の符号記号を指定する
NumberPadding{"",""}
表示長を合わせるために，符号に続けて短すぎる数値にあてがう記号を指定する
SignPaddingFalse
符号の後にスペースを入れるかどうか指定する
NumberFormatAutomatic
数値（仮数部）の出力書式を指定する
ExponentFunctionAutomatic
指数部の出力書式を指定する
数値の表示仕様のオプション
最終の項目を除く，テーブルにあるすべてのオプションは，整数と近似実数の両方に適用される．
上記のオプションはNumberForm，ScientificForm，EngineeringForm，AccountingFormの表記変換関数のどれにでも使える．実際に，表記法に応じて個別に表示仕様を変えることも可能である．表に記載したデフォルト値はNumberFormのものである．
DigitBlock->n で桁の間隔を （ここでは3）にして階乗の値を見やすくする：
区切り記号はなんでもよい．ここでは，スペース（空白）を使ってみる：
正の値にはプラスの符号を付け，小数点の位置にはピリオドの代りに垂直バー(|)を使ってみよう：
実数の表示では，科学表記を使うか使わないかがまず選択される．使うのであれば続いて，小数点以下何桁まで表示するかが決定される．Wolfram言語内部では次の手順で表示様式が決定される．まず，数値を科学表記で記述してみて，そのとき，どのような指数部が生じるかを見る．次に，小数点の左側に桁1つ分のスペースを挿入する．さらに，指数部にExponentFunctionで指定されている変換関数を適用し，実際に表示する形に変換する．このとき，科学表記が使われていなければ，指数部はNull（空）とみなされる．
実数がどう表示されるか見てみよう．特に指定していない場合，指数部がからの範囲以外にある場合は科学表記が使われることになっている：
指数部が10以上の値のときだけ科学表記を採用する記述：
指数部を3の整数倍になるように調整する：
表示したい数の仮数部と指数部を決定したなら，残る最後のステップは，両方の部分を組み合せ最終的に表示する単一オブジェクトを生成することである．ここで，数値の表示書式を任意の形に変えたいときは，オプションNumberFormatを使い書式処理に必要な関数を指定しておく．その関数には，実行時の引数として仮数部，底，指数部の数値の3つの要素が入力されることになっている．指数部を取らない場合は""としておく．
Fortran的な「e」形式で指数部をカスタム表示する：
FortranFormを作用させ正式なFortran形式で数値を表示することも可能である：
PaddedForm[expr,tot]
式にある数のすべてを tot 桁まで表示し，桁数が足りなければ数の手前にスペースを充填して表示長を揃える
PaddedForm[expr,{tot,frac}]
式にある数のすべてを tot 桁まで表示し，小数点以下は frac 桁まで表示し，桁数が足りなければ数の手前にスペースを充填して表示長を揃える
NumberForm[expr,{tot,frac}]
式にある数のすべてを最高で tot 桁まで表示し，小数点以下は frac 桁まで表示する
Column[{expr1,expr2,…}]
式 expri を左揃えで上から下へ1列で表示する
数値表示における表示桁位置の指定
複数の数値を縦1列に表示，もしくは，表形式で表示するとき，個々の数値の桁位置を合わせておくと見やすくなってよい．例えば，表示したい領域において，各数値の位が同じ位置にくるように設定する．
位の位置合せのため，数値の直前と直後に「空白文字（パッド）」を適当に挿入して表示長を調整できるようになっている．通常は，小数点以下の桁が足りなければ，数値の直後（右端）にゼロが付け足される．また，小数点以上の桁の場合は，数値の手前（左端）にスペースがあてがわれる．
表示長を揃えてみよう．スペースがあてがわれ，7桁分の表示長が確保される：
整数のリストを1列に並べて表示してみる：
全表示桁数を7桁とし，その内4桁分を小数点以下の表示に回す：
NumberFormで同じ指定をする．NumberFormでは表示桁長が足りなくてもスペースの充填は行われない：
SignPadding->Trueとすると符号の後にスペースが挿入されるようになる：
科学表記が使われるときは，仮数部だけに桁長の調整が施される：
NumberPaddingのデフォルト設定で関数NumberFormとPaddedFormを使った場合，数値の右側にパッドを入れようとすればゼロが充填される．ここで，左右に充填するものとしてスペースを使いたい場合は，NumberPadding->{" "," "}と指定する．
数値の右にゼロの代りにスペースをあてがうよう指定する：
BaseForm[expr,b]
式に対する数値を底 b に変換し表示する
数値表示における底の変換
入力値を2進法で表示する：
16進法で表示する．10進法以上の場合は，9より大きい数はアルファベットが使われる：
実数にもBaseFormは使える：
科学表記の実数にも使える：
任意の底における数値の入力法と，数値の各位の数字をリストアップする方法は「数の桁」で説明する．必要ならばそちらを参照のこと．
表と行列
Column[list]
要素の列としてタイプセットする
Grid[list]
要素の格子としてタイプセットする
TableForm[list]
表形式で出力する
表と行列の表示形を使ったリスト要素の出力書式の設定
表示例に使う数値リストを作っておく：
Gridはリストを表形式でタイプセットする：
TableFormでリストを表形式で表示する：
GridとColumnは評価しないラッパーであるが，内容を適切な形式にタイプセットする．これらはタイプセットするコンストラクトであり，フロントエンドでの正確な描画を必要とする．
Columnは1列のGridのことである：
GridまたはColumnのFullFormは頭部が不活性であることを示す：
これらのラッパーはすべて，グラフィカルなデータを含むどのような種類のデータをあらわすためにも使用できる：
PaddedForm[Column[list],tot]
tot 桁に十分なスペースを持つようすべての数が充填された列を出力する
PaddedForm[Grid[list],tot]
tot 桁に十分なスペースを持つようすべての数が充填された表を出力する
PaddedForm[Grid[list],{tot,frac}]
すべての近似実数において小数点以下に frac 桁置く
数の右揃え表型表示
数値リストを作っておく：
Columnでリストを1列表示する．
桁数が小さすぎるときは数値手前にスペースをあてがうことで表示桁長を20桁にし，右揃えの列表示をする：
この場合は，Alignmentオプションを使って数を揃えることもできる：
合計8桁，小数点以下5桁の右揃えにする：
SpanFromLeft
左側の要素から伸張する
SpanFromAbove
上の要素から伸張する
SpanFromBoth
上でかつ左の要素から伸張する
Gridで伸張を表すために使われるシンボル
Gridは，第1引数に矩形行列を取る．Gridの各々の要素は伸張する領域を指定することにより，複数の行・列，または矩形の部分格子に渡り伸張することができる．伸張要素は常に伸張領域の左上隅で指定され，残りの領域は適切な伸張記号で埋められる．
以下は伸張する行を示す．伸張する部分はSpanFromLeftを使って埋められる：
同様に，列はSpanFromAboveを使って伸張することができる：
矩形の伸張領域を指定する場合，伸張要素の下かつ右のすべての要素でSpanFromBothが使われる：
オプション名
デフォルト値
BackgroundNone
使用する背景色
BaselinePositionAutomatic
周囲のテキストベースラインに何を揃えるか
BaseStyle{}
格子のベーススタイル指定
FrameNone
格子のどこに枠を描画するか
FrameStyleAutomatic
枠に使用するスタイル
Grid全体の動作に影響を及ぼすオプションの例
FrameオプションはGrid全体の周りに枠を指定することができる：
FrameStyleを使って枠の外観を変更する：
Backgroundを使ってGrid全体の背景色を指定する：
周囲に対するGrid位置はBaselinePositionオプションを使って調整することができる：
次は格子の底辺とベースラインを揃える：
以下はGrid全体のベーススタイルをSubsectionスタイルに設定する：
Columnは1列のGridを指定することに等しい．この2つの関数は類似しているので，どちらにも同じオプションが使える．
Columnに対してGridオプションを設定する：
オプション
デフォルト値
Alignment{Center,Baseline}
項目を水平・垂直方向で揃える
DividersNone
格子のどこに仕切り線を引くか
ItemSizeAutomatic
各項目の幅と高さ
ItemStyleNone
列と行のスタイル
Spacings{0.8,0.1}
水平・垂直方向のスペース
Gridの列と行に影響するオプションの例
個々の行および列に影響を及ぼすGridのオプションはすべて同様なシンタックスを持つ．オプションは{x,y}として指定することができる．ここで x は列すべてに適用され，y はすべての行適用される．また，x と y は単独の値，あるいは各列または行を交代で表す値のリストである．
Alignment設定がない場合，要素は水平方向では中心に，垂直方向ではベースラインに揃う：
以下で，列の水平方向の整列を右に揃えるよう変更する：
各列の水平方向の整列を別々に設定する：
BackgroundあるいはItemStyleオプションが，行と列について異なる設定を指定する場合，フロントエンドは行と列がオーバーラップする設定を組み合わせる．
以下は緑の行がどのようにさまざまな色と組み合わされるかを示している：
以下の例は，行と列の両方で指定されたスタイルをItemStyleがどのように組み合わせることができるかを示している：
複数の行や列に渡って個々の行と列の指定を繰り返したい場合は，リストでラップするとよい．繰り返される要素は，必要なだけ使われる．リストに複数の要素をラップする場合，全体のリストが順に繰り返される．
赤い仕切り線が繰り返される：
ここでは，赤と黒の仕切り線が順に繰り返される：
ItemSizeとSpacingsの両オプションは，水平方向はemで，垂直方向は現行のフォントに基づく線の高さで測定する．また，どちらのオプションもScaled座標を取ることができる．これは，座標が合計のセルの幅あるいはウィンドウの高さを指定するものである．ItemSizeオプションでは，キーワードFullを使うことにより，指定された行または列の要素すべてにフィットするのに必要なスペースを要求することができる．
すべての項目の幅を3emに，高さを1ラインハイトにする：
フォントの大きさを変更すると，異なる大きさで表示される：
以下の例のボタンは，常にセルの幅の4分の1の大きさになる：
Spacingsの最初と最後の設定は，上と下のスペースを2分の1に指定する：
オプション
デフォルト値
Alignment{Center,Baseline}
項目を水平・垂直方向で揃える
BackgroundNone
使用する背景色
BaseStyle{}
項目のベーススタイルの指定
FrameNone
項目のどこに枠を描画するか
FrameStyleAutomatic
枠に使用するスタイル
ItemSizeAutomatic
各項目の幅と高さ
Itemのオプションの例
行および列全体に適用することのできる設定の多くは，Itemラッパーを使ってGridまたはColumnの要素に個別に適用することもできる．Itemを使うと，1つの項目ごとにこれらの設定を変更することができる．Itemレベルで指定された設定は，常にGridあるいはColumnからの全体としての設定をオーバーライドする．
以下で左下の要素に対する項目特定のオプションを設定する：
Itemに対するBackground設定は，Columnの設定をオーバーライドする：
Itemのオプションの多くは，それに対するGridでの設定と同じ設定を取る．しかし，Gridにおいて複雑な行および列を許可するオプションのAlignmentおよびItemSizeはItemの{horizontal,vertical}設定だけしか取らない．
次で，項目の領域をより大きくし，テキストの整列方法を指定する：
ItemSizeオプションの幅の値は改行を決定するために使われる：
ここでItemSizeは，最小の高さを2行分と指定しているが，項目はそれより大きい：

高次元データのフォーマット

Columnは一次元データを，Gridは二次元データをサポートする．任意次元の配列を出力するためには，TableFormを使うことができる．
要素a[i,j]の2×2の配列を均等間隔で表示する：
2×2×2配列を表示する：
さらに，2×2×2×2配列を表示する：
次元の表の表示において，通常，次に続く次元は入れ替りで列，そして，行に割り付けられる．TableDirections->{dir1,dir2,…}の設定条件を与えておけば（ここで，diri は，Columnか Rowを指定する），数値を次元別に列方向，または，行方向に並べることが可能である．デフォルトでは， {Column,Row,Column,Row,…}と交互に並べられる．
並び方向を決めるオプションTableDirectionsを使い，多次元の配列要素の表の構成を指定する：
TableFormは「不揃いな」配列を扱うことができる．要素が与えられていないときは空欄のままとなる．
TableFormなら配列が不揃いでも表示できる：
「副次的な表」を混ぜて表示することも可能である：
オプションTableDepthを使うと，TableFormで表示するリストの最大ネストレベルを指定することができる．
TableFormで表示するが，第2レベル（二次元）以上は表示しないよう指定しておく．サブリスト{x,y}は表の単一の要素として扱われる：
オプション
デフォルト値
TableDepthInfinity
表に含む最大レベル数（次元数）を指定する
TableDirections{Column,Row,Column,…}
各レベル（次元）を行にするか列にするか指定する
TableAlignments{Left,Bottom,Left,…}
各レベルの入力要素をどの方向に寄せて並べるか指定する
TableSpacing{1,3,0,1,0,…}
要素と要素の間隔をスペース記号換算で指定する
TableHeadings{None,None,…}
各レベルに付けるラベルを指定する
TableFormの設定条件
表の要素配置TableAlignmentsを設定することで，表の各入力要素を行や列の辺に合わせて並べることが可能になる．列合せの指定では，左，中央，右(Left，Center，Right)を指定することができる．また，行合せでは，下，中央，上(Bottom，Center，Top)を指定することができる．TableAlignments->Centerと指定すれば，表の全要素が水平・垂直方向で中央に揃えることができる．デフォルトの揃え方に戻すには，TableAlignments->Automaticにする．
通常，表の列要素は左揃えになる：
中央揃えにする：
表の要素間隔TableSpacingを使うと隣接要素の水平・垂直間隔をスペース記号の単位で指定できる．0とすれば，間隔なしになる．
列と列の間をスペース記号6個分にし，行と行の間は間隔なしにする：
None
ラベルを付けない
Automatic
番号ラベルを付ける
{{lbl11,lbl12,…},…}
任意のラベルを各レベルに付ける
オプションTableHeadingsの設定
2×2×2配列に番号ラベルを付ける：
行には番号ラベルを付け，列には指定の文字列ラベルを付ける：
行にだけラベルを付ける．3番目のラベルに相当する行がないので，TableFormは自動的に空の行を挿入する：
出力におけるスタイルとフォント
Style[expr,options]
設定条件に基づいて式を出力する
Style[expr,"style"]
セルスタイルに基づいて式を出力する
出力スタイルの指定
2番目の を太文字表示にする：
10ポイントから20ポイントの大きさでtextを表示する：
文字列をHelveticaフォントで表示する：
Styleではいくつかのオプションについて短縮した形が使える．FontSize，FontWeight，FontSlant，FontColor等のオプションについては，オプションの設定だけを含むことができる．
ここではオプションが短縮された形式で指定されている：
オプション
設定例
FontSize12
文字の大きさ
FontWeight"Plain"
または
"Bold"
文字の太さ
FontSlant"Plain"
または
"Italic"
斜体指定
FontFamily"Courier"
，
"Times"
，
"Helvetica"
文字の種類
FontColorGrayLevel[0]
文字の色
BackgroundGrayLevel[1]
背景色
Styleのオプション
ノートブック用フロントエンドを使っている場合，出力する式は，出力セルのデフォルトスタイルに従い表示される．Style[expr,"style"]を使えば，任意のスタイルで式を表示できる．
セクションの見出しに通常使うスタイルを出力される式に適用してみる：
「Wolfram言語式としてのセル」に，セルのスタイルをどう使うか詳しい説明があるので参照のこと．Style[expr,"style",options]を使うと，特定のスタイルではあるが，あるオプションが変更された出力が生成できる．
ボックス形テキスト表記
テキスト表記の式は，究極的にすべてボックスの集合として表せる．ボックスとは二次元的に相対配置されるオブジェクトを指す．
a+bの式を表すボックスである：
DisplayFormを作用させ，ボックスがどう表示されるか見てみる：
DisplayForm[boxes]
ボックス boxes を数学表記で表示する
ボックスの表示
3つの文字を1行に並べる：
2番目の文字を下付き文字として表示する：
下付き文字ボックスを2つ横に並べる：
"text"
文字列
RowBox[{a,b,…}]
ボックスの行あるいは文字列 a,b,…
GridBox[{{a1,b1,…},{a2,b2,…},…}]
ボックスの配列
a1b1…
a2b2…
⋮⋮
SubscriptBox[a,b]
下付き文字ボックス ab
SuperscriptBox[a,b]
上付き文字ボックス ab
SubsuperscriptBox[a,b,c]
上付き下付き文字ボックス
UnderscriptBox[a,b]
真下付き文字ボックス
OverscriptBox[a,b]
真上付き文字ボックス
UnderoverscriptBox[a,b,c]
真上真下付き文字ボックス
FractionBox[a,b]
分数ボックス
SqrtBox[a]
平方根ボックス
RadicalBox[a,b]
b 次根
基本的なボックス
根号の中に分数を入れるためボックスをネストさせる：
文字書式ボックスを組み合せ，上付き文字を下付き文字の後に付ける：
1つのボックスで，上付き文字と下付き文字を一括で作る：
FrameBox[box]
ボックス box の周囲に罫線を描く
GridBox[list,RowLines->True]
グリッドボックスGridBoxの行と行の間に罫線を引く
GridBox[list,ColumnLines->True]
列間に線を引く
GridBox[list,RowLines->{True,False}]
第1行の下だけに罫線を引く
罫線
分数の周囲に罫線を引く：
配列の列と列の間，そして，行と行の間に罫線を引く：
その周りにも罫線を引く：
StyleBox[boxes,options]
ボックス boxes に書式を適用する
StyleBox[boxes,"style"]
ボックス boxes にスタイルを適用する
ボックスの書式変更
StyleBoxの条件設定の仕方はStyleと同じである．両者の違いは，Styleが式の表示方法を決定するよう式に対して適用される高レベル関数であるのに対し，StyleBoxは根底にあるボックス構造においてそれに対応する低レベル関数であるという点である．
文字列「名前」のフォントサイズを6にする：
今度は，文字列を現在のノートブックに登録されている見出し用スタイルで表示させる：
見出し用スタイルを使うが，文字は灰色で表示させる：
ノートブック用フロントエンドを使っている場合，スタイルや表示書式はメニューを介して直接変更できる．それでも内部では，書式変更があるたびにStyleBoxのオブジェクトが挿入される．
FormBox[boxes,form]
ボックス boxes に表記 form に関連した規則を適用する
InterpretationBox[boxes,expr]
ボックス boxes が指定式 expr を表すものと解釈する
TagBox[boxes,tag]
ボックス boxes にタグ tag を関連付けて解釈する
ErrorBox[boxes]
エラーの旨を告げ，ボックス boxes の解釈処理を停止する
ボックスの解釈
xに上付き文字を付けて表示する：
式に変換すると，ベキとして解釈される：
xに上付き文字が付いて表示される：
ただし，今度はInterpretationBoxの指定があるため，vec[x,2]として扱われる：
InterpretationBoxにあるボックスを編集してしまうと，解釈用情報が不正になってしまうかもしれない．これを防ぐためにInterpretationBoxオブジェクトの選択や編集を制限するオプションが各種用意されている．
オプション
デフォルト値
EditableAutomatic
オブジェクト内容が編集可能かどうか指定する
SelectableTrue
オブジェクト内容が選択可能かどうか指定する
DeletableTrue
オブジェクト内容が削除可能かどうか指定する
DeletionWarningFalse
オブジェクト内容が消去される際は警告するかしないか指定する
BoxAutoDeleteFalse
オブジェクト内容が変更された際はボックス書式を除去するかしないか指定する
StripWrapperBoxesFalse
TagBox[boxes,…]にあるボックス boxes からStyleBox等を自動的に除去するかしないかを指定する
InterpretationBoxと関連するボックスのオプション
TagBoxを使うと，ボックスの内容を解釈しやすくする情報を付加しておくことが可能である．例えば，ボックス boxes に対応する式の頭部を tag という関数にするには，TagBox[boxes,tag]と指定する．オブジェクトを編集しても，それが引数だけなら，オブジェクトと関数の関連付けは残るのでTagBoxは引き続き的確であると解釈できる．ボックスを編集可能にしておくため，Editable->Trueのデフォルトの条件が事実上TagBoxに与えられている．
各種の規則がボックスの内容に適用され，式の解釈が行われる．規則の適用において，通常，StyleBoxオブジェクト等の書式指定は無視される．このため，StripWrapperBoxes->Falseの条件があらかじめ設定していなければ，例えば，文字色が赤でもxなら文字色が黒の普通のxと同じにみなされてしまう．
文字色が赤でも，xは通常，普通の黒のxと同じに扱われる：
ボックスの文字列表記
ボックスオブジェクトを文字列でコンパクトに表すこともできる．文字列表記を使うとボックスの仕様をテキスト書式でインポートやエキスポートするのに便利である．
SuperscriptBoxを作る：
ToExpressionを作用させる．SuperscriptBoxがベキ乗として認識されるのが分かる：
単なる表示用ボックスと演算上意味のあるボックスは記述上違うので注意する．
この記述は単に上付き文字として表示するSuperscriptBoxである：
こうするとSuperscriptBoxの表すベキ乗を意味するようになる：
ベキ乗として扱われたか確かめてみる：
∖(input∖)
内容をボックス表示する
∖!∖(input∖)
内容を演算上意味のあるボックスにする
単なるボックス表示と演算的意味付けの記述上の違い
テキストエディタ等の外部プログラムにStandardFormのセル内容をコピーすると，∖!∖(…∖)の書式が必要に応じて使われ式がコピーされる．この書式を使っておけば，ユーザが式をWolframシステムにコピーし直しても，自動的に式をStandardFormで再構築できる．∖!を付けておかないと，単なるボックス表示しかしない式になってしまう．
ノートブックに∖!∖(…∖)の形でペーストした式は通常，二次元的な数学表記で表示される．
"∖(input∖)"
単なる文字列
"∖!∖(input∖)"
ボックスを含む文字列
文章にボックスオブジェクトを組み込む方法
文字列中に起る∖(…∖)の形の記述は単なる文字の羅列としか扱われない．これに対して，∖!を追加した形なら，記述文はボックスを表すものとして扱われる．ボックスオブジェクトを普通の文章に組み込むにはこの方法を使うとよい．
この記述だと，単なる文字列としか扱ってくれない：
\!を加えると，文字列がボックスを含むことになる：
文章にボックスを混ぜる：
∖(box1,box2,…∖)RowBox[box1,box2,…]
box1∖^box2SuperscriptBox[box1,box2]
box1∖_box2SubscriptBox[box1,box2]
box1∖_box2∖%box3SubsuperscriptBox[box1,box2,box3]
box1∖&box2OverscriptBox[box1,box2]
box1∖+box2UnderscriptBox[box1,box2]
box1∖+box2∖%box3UnderoverscriptBox[box1,box2,box3]
box1∖/box2FractionBox[box1,box2]
∖@boxSqrtBox[box]
\@box1\%box2RadicalBox[box1,box2]
form∖` boxFormBox[box,form]
\*input
input の解釈から適切なボックスオブジェクトを作成する
ボックスの文字列表記
ボックスオブジェクトの記述は∖(と∖)でくくっておかなければいけない．一番外側の∖(と∖)の内側になら，∖(と∖)のペアをいくつも使いネスト形のボックス構造を構成できる．
カッコを使い式の項をまとめる：
カッコを使わないと項のまとめ方が変わってしまう：
∖(と∖)も項のまとめに使うが，表示には現れない：
内側にある∖(と∖)のペアはRowBoxの構成に使っている：
例えば，aa+bbと式を入力すると，カーネルでaa，+，bbの成分に分解される．各成分はシンボルとして扱われる．∖(…∖)の記述を使いボックスオブジェクトを入力したときもシンボルの分解が行われる．ボックスの入力では文字列の形でシンボルが与えられ，式の入力では演算的に意味ある成分として与えられる，という点が違う．
入力すると，RowBoxになりaa，+，bbの各文字列に分解する：
+ 記号の両脇にスペース記号を入れたが，表示には出ない：
ネストしたRowBoxオブジェクトを2つ作る：
スラッシュ記号(/)の後に何も続けなくても，上の例と同じ形のボックスが作られる：
∖(…∖)の内側で記述すれば，∖^と∖@のバックスラッシュ記述のボックスを構成できる．他の種類のボックスは，∖*に続ける形で標準のWolframシステム式として入力しなければいけない．
GridBoxを作る：
StyleBoxを作る：
∖*はエスケープのように振る舞い，∖(…∖)の記述中に式を挿入する場合に使う．∖*に続ける式の記述の中には，別の∖(…∖)の記述を入れても構わない．
∖*と∖(…∖)の記述を交互に入力しても構わない．引用符は∖(…∖)記述の外に出しておく：
∖!∖(input∖)
入力を現行の表記法で解釈する
∖!∖(form∖`input∖)
入力を指定の形で解釈する
表記法に依存した記述の解釈
セルがStandardFormになっていれば，StandardFormとして解釈される：
TraditionalFormとして式を解釈するよう特別に指定する：
テキストエディタ等の外部プログラムへセルの内容をコピーすると，バックスラッシュとバッククォートはコピー内容に明示的には含まれない．ただし，別の種類のセルから式をペーストする際は，バックスラッシュとバッククォートを加えておかないと正確な解釈が行われなくなってしまう．
文字列，ボックス，式の間の変換
ToString[expr,form]
式 expr を指定されたテキスト表記の文字列に変換する
ToBoxes[expr,form]
式 expr を指定されたテキスト表記のボックスに変換する
ToExpression[input,form]
文字列またはボックスを指定されたテキスト表記の式に変換する
ToString[expr]
OutputFormの文字列に変換する
ToBoxes[expr]
StandardFormのボックスに変換する
ToExpression[input]
StandardFormの式に変換する
文字列，ボックス，式の間の変換
簡単な式を入力する：
InputFormの文字列に変換する：
FullFormを使うと引用符が文字列に付く：
StandardFormのボックスに対応する文字列が返ってくる：
ToBoxesでボックスに変換してみる：
ファイルや外部プログラムのデータを生成する際，通常のキーボード上の文字だけを使う，二次元的な記述が必要とされることがある．これはOutputFormを使って行うことができる．
キーボードにある文字記号だけを使い数学表記の式を構成し，文字列に変換する：
文字列には∖nの改行コードが入れられ2行構成になっている：
等幅のフォントでないと正確に表示できない：
行モード的な入力だけしかしないのなら，ToStringを使い文字列の変換操作ができる．
StringFormのOutputFormに対応した文字列を生成する：
InputForm
キーボード入力主体の文字列要素からなる表記
StandardForm
数学記号等の標準的な表示・編集機能に対応した文字列とボックス要素からなる表記（デフォルト形式）
TraditionalForm
慣用的な数学表記に基づいた表示・編集機能に対応した文字列とボックス要素からなる表記
式への変換機能(ToExpression)で有効な表記の例
InputFormの式を文字列として入力し，計算できる式に変換する：
StandardFormのボックス記述から計算可能な式に変換する：
TraditionalFormなので，関数として解釈される：
ToExpression[input,form,h]
式を生成し，その式に頭部 h を作用させる
式に頭部を作用させる
入力すると直ちに式に変換され計算される：
StandardFormの式に変換し評価保留用関数の頭部Holdを作用させる：
Hold解除のためReleaseHoldを作用させる：
SyntaxQ["string"]
文字列の式が文法的に正確しいWolfram言語の入力かどうか検査する
SyntaxLength["string"]
文字列が式を表すものとして，先頭からどの位置の文字までが文法的に正確な式の要素を表しているか調べる
文字列としての入力式の正確性の判定
式の変換関数ToExpressionは，どのような内容の文字列であれ，とりあえずは式として解釈を進める．このため，式として本来機能しない間違った記述文を与えると，変換不能になり失敗のメッセージが表示され，$Failedが返ってくる．
式をテキスト形式で入力する．文法的に間違っているので，ToExpressionは変換できない：
ToExpressionで正常な変換をするにはWolfram言語の認識可能な完全な式でなければいけない：
SyntaxQの機能を使いWolfram言語の文法上，文字列が正確に式を表しているか判定できる．SyntaxQの答がFalseであれば間違いがあるので，SyntaxLengthを使い文字列のどこでエラーが起ったか調べる．SyntaxLengthでは文法エラーが起る地点まで検査にパスした文字数が得られる．
SyntaxQで式に誤りがないか調べる：
誤りがどこで起ったかSyntaxLengthで調べる．位置3で誤りが検出されたことが分かる：
SyntaxLengthを使うと文字列の長さより大きい値が返ってくる．これは，入力した部分に関しては問題がないが，それに続くはずの要素が見付からなかったことを意味している：
Wolfram言語の文法
Wolfram言語の文法は組込み済みの変換規則から形作られている．文法の規則に従いテキスト形，ボックス形の式が計算可能な式に変換される．規則の中でも特にStandardFormとInputFormに対応した規則は重要で，それらがWolfram言語の中核を構成している．TraditionalFormに対応した規則は目的は前者と同じだが詳細で異なる．
a
,
xyz
,
αβγ
代数記号
"some text"
,
"α+β"
文字列
123.456
,
3*^45
数値
+
,
->
,
≠
演算子
(*コメント*)
評価上意味のない入力文
Wolfram言語における記述成分
テキスト形式で式を入力すると，Wolframシステムによって演算上意味のある成分に分解される．
例えば，xx+yy-zzzzと文字列を入力したら，xx，+，yy，-，zzzzの各成分に分解される．xx，yy，zzzzは代数記号を表すシンボルとして扱われ，+と-は演算子として扱われる．
式の演算子が式の構造を決定する．Wolfram言語で有効な演算子は次の表に示す種類がある．種類により演算子と被演算子の相対的な位置関係が違う．
接頭辞（前置形）
!xNot[x]
接尾辞（後置形）
x!Factorial[x]
接合辞（中置形）
x+y+zPlus[x,y,z]
整合辞
{x,y,z}List[x,y,z]
複合形
x/:y=zTagSet[x,y,z]
上方演算子
OverHat[x]
Wolfram言語における演算子の種類と例
演算子が正確に機能するには所定の位置に被演算子が配置されていることが必要不可欠である．式に複数の演算子があるときはどの演算子が被演算子を先に取り出すかによって式の解釈に違いが出る．
例えば，a*b+cと入力したら，*と+のどちらが被演算子を先に取り出すかで，(a*b)+cかa*(b+c)のどちらにもなり得る．
まぎらわしさを解消するため，演算子には固有の優先度が割り当てられている．優先度が高ければ高いほどその演算子の被演算子がより先に取り出されることになる．
上の例の場合は，乗算*は加算+より優先度が高いので，乗算の被演算子がまず取り出される．従って，a*b+cはa*(b+c)ではなく，(a*b)+cと解釈される．
乗算*は加算+より優先される．どちらの場合もTimesの関数参照が内側にきている：
//は優先度が低いので，この式では最後に適用される：
@は優先度が高い：
演算子の優先度がどうであろうと，カッコで式の要素を適切に囲うことで任意の評価順序を強制できる．
カッコで加算項をくくったので，TimesではなくPlusが内関数になる：
代数記号の拡張指定
x_
，
#2
，
e::s
，等
関数適用の指定
e[e]
，
e@@e
，等
ベキ数の指定
√e
，
e^e
，等
乗算関連の演算指定
∇e
，
e/e
，
e⊗e
，
ee
，等
加算関連の演算指定
e⊕e
，
e+e
，
e⋃e
，等
関係記号
e==e
，
e∼e
，
e⪡e
，
e⧏e
，
e∈e
，等
ベクトル量の指定
e⟶e
，
e↗e
，
e⇌e
，
e⥓e
，等
論理演算記号
∀ee
，
e&&e
，
e∨e
，
e⊢e
，等
パターン・規則の指定
e..
，
e|e
，
e->e
，
e/.e
，等
純粋な関数の指定
e&
割当て記号
e=e
，
e:=e
，等
複文型の式の指定
e;e
演算子の種類と例
「演算子の入力形」の表に，演算子や特殊記号が優先度の高い順に列記してあるので参照のこと．*や+等の多くの演算子の優先順位は数学で使う標準的な順位に対応して設定してある．全体の順位はなるべくカッコを使う必要がなくなるように設定してある．
カッコでくくらなくても演算順位通りの評価順序になる：
FullFormでどのような構造の式が構築されたか確認してみる：
最初の要素にはカッコがないが2番目の要素と同じになる．つまり，カッコを付けても付けなくてもよい．3番目の要素はカッコでくくる必要がある：
どれも優先しない
x+y+zx+y+z
先頭ペア要素から評価
x/y/z(x/y)/z
末尾ペア要素から評価
x^y^zx^(y^z)
接合辞型の演算子の評価形態別分類
加算の評価順序を見てみよう．関数Plusには引数がいくつあってもよいFlatな関数なので，グループ化は行われない：
次に，ベキ乗の評価順序を見てみる．関数PowerはFlatではないので，要素のグループ化が行われる：
Wolfram言語の文法は，キーボードから直接入力できる文字・記号だけでなく，Wolfram言語の提供する数々の特殊文字や記号にも対応している．
，， 等の特殊文字も標準アルファベット文字と同様に扱われるし，代数記号としても使える．また，，，等の特殊記号も同じように使える．
特殊記号によっては演算子として働くものもある．例えば，と は中置形の演算子だし， は前置形の演算子である．また，とは整合辞形の演算子である．
とは中置形の演算子である：
は掛け算の演算子で記号*と作用は同じである．中置形の演算子でもある：
特殊記号のいくつかは組み合せることによって，複合形の演算子を形成する．例えば，積分式 ∫fxには ∫ と の特殊記号がセットで使われる．2つ合わせてはじめて機能するので，複合形の演算子といえる．
∫ と を組み合せて積分式を構築する：
評価優先度から考えると，∫… の優先度はTimesよりも低いので，カッコは不要である：
この式ではカッコを使わなければいけない：
式の入力は一次元的な行モード入力だけでなく，二次元的な数学表記のボックス形式で入力してもよい．二次元的な入力形態もWolfram言語の文法でカバーしている．
上付き文字のボックス要素はベキ数の指数部と解釈される：
偏微分記号 ∂xf はボックス形の複合形演算子を形成する：
はより複雑な複合形演算子の一部になっている：
演算子としての は+より優先度が高いことに注意：
演算機能が未定義の演算子
2+2と入力すると，+が演算子として最初に認識される．結果として式Plus[2,2]が内部で構築される．次に，Plusについて既知の規則が適用され式が評価され，評価結果4が出力される．
ただ，演算子の中には，演算機能的な意味を持たないものもある．Wolfram言語には数百に及ぶ補助的な演算子が提供されており，式の構築に使用できるが，デフォルトの評価規則は特に定義されていない．
これらの記号に演算機能を組み込み，ユーザ定義の演算子として使える．
は中置形の演算子として動作可能だが，機能は何も定義されていない．このため，式は評価されない：
StandardFormでは，は中置形演算子として表示される：
に演算機能を定義する：
今度は，は演算子として認識されるだけでなく，実際に評価も実行される：
x⊕yCirclePlus[x,y]
x≈yTildeTilde[x,y]
x∴yTherefore[x,y]
x↔yLeftRightArrow[x,y]
∇xDel[x]
xSquare[x]
〈x,y,…〉AngleBracket[x,y,…]
演算機能が未定義の一次元形演算子の例
演算子に関連付けられる関数は演算子の名前と同じ名前を持つようになっている．
演算子\[Congruent]を入力するとと表示される：
内部表記を見てみるとCongruentの名前の関数になっている：
x \[name] y
name [ x , y ]
\[name] x
name [ x ]
\[Leftname] x,y,…\[Rightname]
name [ x , y , … ]
演算子と関数名の対応
デフォルトではCirclePlusやCircleTimesの関数には演算機能的な意味付けはされていないが，演算子 およびとしては，評価優先度が割り付けられている．「演算子の入力形」の表にWolfram言語で使える演算子のすべてが優先度順に列記してあるので参照のこと．
との評価順序を見てみよう．よりが優先される：
xySubscript[x,y]
x+SubPlus[x]
x-SubMinus[x]
x*SubStar[x]
x+SuperPlus[x]
x-SuperMinus[x]
x*SuperStar[x]
x†SuperDagger[x]
Overscript[x,y]
Underscript[x,y]
OverBar[x]
OverVector[x]
OverTilde[x]
OverHat[x]
OverDot[x]
UnderBar[x]
演算機能が未定義の二次元形演算子の例
下付き文字指定記号には演算機能としては何も定義されていない：
普通の上付き文字指定記号はベキ乗の機能があらかじめ定義されている：
上付き指定記号によってはベキ乗としては認識されないものもある：
OverBarとOverHatは機能が未定義なので，どんな評価規則でも割り付けられる：
出力書式の定義
入力式の評価法をカスタマイズできるように，出力式の表示書式もカスタマイズできる．カーネルから式が出力される前に書式変更関数Format[expr]が適用される．この関数にカスタム書式をあらかじめ指定しておけば，式の表示様式を自由に変えれる．具体的には，指定したい書式をボックスオブジェクト等で構成し，書式変更関数Format[expr]に割り当てておく．関数が出力式に適用されると，ボックス形の書式に対応した数学記号等が使われ式がカスタム表示される．
binの要素をグリッドボックスとして表示するよう書式変更関数を定義しておく：
数学の二項係数の形でbinの項が表示される：
内部表記を見てみると，binの項はそのままになっている：
Format[expr1]:=expr2
第1式 expr1を書式指定用第2式 expr2に変換する
Format[expr1,form]:=expr2
特定の出力表記のときだけ書式変換を実行する
出力式の書式変更
このように，書式変更関数Formatを個別に定義しておくことで，特定の式を別の形で表示できる．さらに，特定の要素に対応した書式変換法をプログラムに記述しておき，プログラム全体を書式変更関数に割り付けておけば，より複雑な変換が実現できる．
簡単なプログラムを使いxrepを書式変換するように関数を定義しておく：
書式変換されるとxrepの各要素が引数に対応した長さの文字列の形で表示される：
それでも，内部では，xrepの要素のままである：
Prefix[f[x],h]
接頭辞（前置形） h x
Postfix[f[x],h]
接尾辞（後置形） x h
Infix[f[x,y,…],h]
接合辞（中置形） x h y h…
Prefix[f[x]]
標準の接頭辞（前置形） f@x
Postfix[f[x]]
標準の接尾辞（後置形） x//f
Infix[f[x,y,…]]
標準の接合辞（中置形） x~f~y~f~…
PrecedenceForm[expr,n]
優先度 n の要素をカッコでくくる
演算子の表示型と表示位置の指定
fを前置形の演算子とし，表示上の演算記号を<>とする：
中置形の演算子<>を使い表示する：
演算子<>は+より優先度が高いのでカッコでくくる必要がない：
出力する式にいくつも演算子がある場合，どの演算子の引数をカッコでくくる必要があるのだろうか．また，どうやって見分けるのだろう．実は，演算子の評価優先度に応じてカッコが使われることになっている（「式の特殊な入力法」を参照のこと）．デフォルトの優先順位が適当でない場合は，関数PrecedenceFormを使い演算子の優先度が変えられる．指定可能な優先度は1から1000のレベルで，高い値ほど高い優先度を意味し，また，カッコが不要になる方向である．
に優先度100を割り付ける．この優先度は低すぎるため，カッコが使われ要素がグループ化される：
Format[expr]で式 expr に対応した変換書式を定義すると，現行の出力表記が標準的な出力表記のいずれかである限り変換書式は有効である．また，Format[expr,form]を使えば表記法を限定した上で式 expr の書式変換ができる．
TeXFormの表記が使われているときに限り，xに書式変換を施す：
TeX表記で出力させると，上の定義が有効になり，xの表示書式が変わる：
低レベル入出力の規則
MakeBoxes[expr,form]
式 expr を指定表記法のボックス形に記述変換する
MakeExpression[boxes,form]
ボックス boxes を指定表記法の式に逆変換する
式とボックスの変換用の低レベル関数
MakeBoxesは，入力式を評価しないままボックス形に変換する：
ボックス形の式を計算可能な式に変換する．ただし，保留関数HoldCompleteが適用され，実際の計算は行われない：
Wolfram言語には入力式の解釈と出力式の生成のために膨大な数の規則が組み込まれている．それらの規則は，特に，StandardFormにおいて矛盾がないように設定されている．したがって，StandardFormの入出力では入力用の式と出力用の式が交換可能になる．
演算子の処理規則をカスタマイズすることは非常にまれであろう．それは必要がないからである．Wolfram言語には多くの機能上未定義な演算子に関しても，入出力処理で使う規則がすでに組み込まれているからである．
例えば，乗算演算子の一般形を作るならば，等の演算子に入出力処理の規則がすでに定義済みなので，それを使えば用が足りる．
出力式がの演算子で表示される：
また，入力するとが演算子であることが認識される：
Format[expr]を使い特定の式を特殊書式で表示させる方法は説明したが，一度書式変換した出力式は入力式としては使えなくなってしまうので気を付ける．
必要ならば，基本的な入出力の処理規則から定義し直すことも可能である．つまり，MakeBoxesとMakeExpressionの割付け式を定義する．ただし，少しでも間違った定義をすると，矛盾してしまうので十分な注意が必要である．
StandardFormにおいてgplusをどう表示したらよいか詳細な指定をする：
gplusが添数付きの演算子として表示される：
関数としては定義していないので評価されない：
添数付きのをFullFormの入力として扱うよう割付け式を定義する：
この記述は入力式として解釈できない．添数付きのはgplusとして扱われる：
MakeBoxesを使い規則を定義することは，基本的にFormat機能を使った変換書式の定義付けの低レベル版に相当する．両者の違いは，MakeBoxesでは引数の評価は行われないが，Formatでは行われるということにある．したがって，前者を使うときは，変換した式が評価処理を経てどうなるかは全く気にせずに変換規則を組み立てることができる．
さらに，Formatは，それを使って変換して得られた二次的な式に対して再度自動的に適用される．MakeBoxesは動作が異なり，二次的な式に変換を要するものがあっても特別にMakeBoxesを適用しない限り変換は起らない．
■ 評価最小単位の要素に分解する．
■ スペース記号等を除去する．
■ 評価優先順に従いボックスを構築する．
■ スタイルボックス( StyleBox )等の評価に無関係なオブジェクトは除去する．
■ MakeExpression用の変換規則を適用する．
入力式に施される処理手順
構造化されていない式の出力
「式のテキスト形入出力」についてのチュートリアルで説明した関数は表示用の書式をどう変更したらよいか指定するもので，実際の表示作業自体は行わない．
普通，式が処理され出力されると，特にユーザがコマンドを出さなくても自動的に出力式が表示されるようになっている．通常Wolfram言語は，与えられた入力を処理することで得られた最終的な結果を自動的に出力する．それでも，計算式によっては，各計算段階で暫定的な結果を逐次表示できると便利である．そのようなときは，関数Printを使う．
Print[expr1,expr2,…]
式 expri を間隔なしで列記する（列記終了時に改行する）
式のプリント
Printは間隔なしで引数を表示するが，最後には改行が入る：
整数と平方根が縦に2列表示される：
関数Printは，先に与えられた引数から順番に，間隔なしで引数をそのまま列記する．書式を付けて表示させたければ，Printの引数部に適当な書式変換用の関数を適用しておけばよい．
行列を表の形で表示する：
StringFormを使い書式付きで計算値を表示する：
Printはテキストとグラフィックスが混在していても使える：
Printで式や文を出力すると，通常，標準的な出力表記で表示される．特別に表記法を指定すればその限りではない．
出力式を入力形に変換してから表示する：
Wolfram言語にはPrintの他にも出力機能がいくつか用意されている．例えば，「メッセージ」に記載してあるようにMessageと呼ばれるタグ付きメッセージを出力する関数がある．さらに，「ストリームと低レベルの入出力」に記した低レベルの関数を使えば，ダイアログセッションにおけるユーザとのやり取りやファイル処理や外部プログラムとのやり取りでカスタム書式で式や文を表示することも可能である．
Printと全く同様に動作するが，最終評価が終わるまで出力だけしか表示しないコマンドに，PrintTemporaryがある．
フォーマット出力
Wolfram言語はバージョン3以来，任意の数学タイプセットおよびレイアウトに対して十分なサポートを提供してきた．そのパワーの根底にあるのは「ボックス言語」と呼ばれるものであり，これによりノートブック自体がWolfram言語式となるのである．このアプローチは非常に強力になり，Wolframシステムの多数のユニークな機能の基礎を形成した．しかし，ボックス言語のパワーにかかわらず，実際にユーザが直接アクセスするには難しいものであった．
バージョン6から，ボックスを直接使用する面倒くささをほとんど排除しながらも，同じタイプセットおよびレイアウトのパワーがすべて使用できる，このボックス言語の高レベルインターフェースが導入されている．この新しい層の関数は「ボックスジェネレータ」と呼ばれるが，ボックス言語を効率的に使うためにそれを認識しておく必要はない．このチュートリアルでは，広範な式の表示に適したボックスジェネレータを見て，それを使って簡単な数学タイプセットを超えた，きれいにフォーマットされた出力を生成する方法を紹介する．

出力の書式設定

Wolframシステムフロントエンドは，フォントの特性の変更メニューを含む，ワープロで使用できる通常のスタイル機能をすべてサポートする．しかし，生成された出力で自動的にこれらのスタイル機能にアクセスすることは非常に難しかった．出力は引き続きほとんど一般的に標準の12ポイントCourier（TraditionalFormを使っている場合はTimes）である．これを修正するために関数Styleが作成された．Style式を評価するたびに，その出力は指定されたスタイル属性をアクティブにして表示される．
Styleはどのような種類の式にもラップすることができる．以下の例は，Styleで異なるフォントの重みと色を使った素数および合成数を表示する．
Styleで適用することのできるフォーマットオプションは何百もある．詳細はStyleのドキュメントに記載されている．以下にリストするのは，最も一般的なもののいくつかである．
メニュー
Style[] オプション
Style[] 指示子
書式 ▶ サイズ ▶ 14FontSize->1414
書式 ▶ 文字の色 ▶ 灰FontColor->GrayGray
書式 ▶ 文字飾り ▶ 太字FontWeight->BoldBold
書式 ▶ 文字飾り ▶ 斜体FontSlant->ItalicItalic
書式 ▶ 背景色 ▶ 黄Background->Yellow
書式 ▶ フォントFontFamily->"Times"
書式 ▶ スタイル ▶ Subsection"Subsection"
Styleは任意の数だけネストすることができ，競合があった場合は最も内側のものが優先される．以下ではリスト全体にStyleをラップし，リストのすべての要素に新しいフォントを適用する．
他に一般的に望まれることは，出力の一部をテキストのようなスタイルにしたいという場合がある．コードで使用することを意図したフォントでテキストが表示されると非常におかしく見えることがある．そのため，関数Textで引数が常にテキストフォントで描画されるようにする（Wolframシステムグラフィックスに詳しい人はText関数をグラフィックスプリミティブと認識するだろうが，そのように使ってもグラフィックス外ではグラフィックスプリミティブとしての使用とは競合しない）．
Styleはフォントに関するオプションだけではなく，どのオプションがアクティブであるスクリーン上の領域を設定するために使うことができる．このチュートリアルの後半では，StyleがGridやTooltip等の他のフォーマットコンストラクトの属性の表示にどのように影響を与えることができるかを説明する．

格子のレイアウト

二次元レイアウト構造を使うことは，その構造にスタイル指示子を適用するのと同様に便利である．Wolfram言語では，そのようなレイアウトのための主な関数はGridである．Gridには配置，枠要素，伸張要素等のものを任意に調整することのできる機能を含む，非常に柔軟なレイアウト機能がある（他のチュートリアルでGridの機能について詳しく述べているので，ここでは要点だけを説明する）．
ここでもう一度，素数と合成数とを別々に表示するStyleの例題を見てみる．
これをGridに入れ，まずPartitionを使いこの100個の要素を10×10の配列にする．Gridに不揃いな配列（要素がころなる長さのリストとなっているリスト）を与えることもできるが，ここでは規則的な配列を与える．結果の表示はきれいにフォーマットされたレイアウトになる．
列は中心に配置され，枠の線はない．Gridのオプションを使うと，このどちらでも簡単に変更することができる．
Gridのオプションすべてとそのシンタックスについての詳細は，このドキュメントの範疇を超えるが，オプションを使って驚くようなことができる．詳細はGridのドキュメントを参照のこと．
Gridに関連した便利なコンストラクトがいくつかある．そのうちのひとつはColumnであり，要素の平坦なリストを取りそれらを縦に配列する．これをGridで行うと少しおかしくなる．次の簡単な例では列のオプションを見る．
ではリストを横に並べるにはどうすればよいか．この場合，問題は結果の表示を数式やテキストの行のように改行したいか，1行にとどめたいかである．後者の場合，Gridを1× n 配列に適用する．
しかし，以下の例題では格子全体が使用可能なウィンドウ幅に合うように縮小されている．その結果，グリッドの要素で複数行に改行されるものもでてくる．これはGridのデフォルトのItemSizeオプションのために起る．格子の要素が自然の幅になるようにするためにはItemSizeをFullに設定する．
もちろんこれで，このウィンドウ幅を大きく広げない限り格子全体が1行に収まらないほど広くなった．そのため見えない格子の要素もある．ここで別の水平レイアウト関数のRowが役に立つ．
Rowに要素のリストを与えると，結果全体がテキストや数式の行のように自然に改行される．この種のレイアウトは昔の（現在では使われていない）SequenceForm関数を使ったことのある人にとっては馴染みのあるものであろう．
ご覧の通り，Rowはデフォルトで要素間にスペースを空けない．しかし第2引数を与えると，その式は要素間に挿入される．以下ではコンマを使っているが，どのような式でも使える．
ノートブックウィンドウの大きさを変更すると，ItemSize->Automaticという設定のGridがRowとは異なる動作をするのが分かる．どちらも状況に応じて便利である．

入力としての出力の使用

ここでStyle，Grid，その他すべてのボックスジェネレータは，出力に固執するということを述べておきたい．StyleあるいはGridにより生成されたあるフォーマットを持つ出力の一部を取り，それを入力として再利用する場合，文字通りのStyleあるいはGrid式が入力式に現れる．昔のStyleBoxあるいはMatrixForm等の関数に慣れている人は，これが変更点であると分かるであろう．
埋め込まれたスタイルを多数含んでいるこのGridコマンドの出力を取り，ある入力式で使ってみる．
格子は格子のままであり，色も青いまま，また要素も前と同様太字とグレーのままである．また，文字通りのGridおよびStyleを式に入れると，スカラーを行列に加えたものと干渉し，結果がベキ乗になる．これらの複合構造はほとんど常に自動的に解釈されないようにしたいものであるから，この違いは非常に重要である．しかしながら，そのようにしたい場合は，ラッパーを外しデータを得ればよいので簡単である．

特殊な格子要素

Gridは，より柔軟な2Dレイアウトを作成するために，項目としてSpanFromLeftのような2，3の特殊シンボルを取る．項目SpanFromLeftは格子のすぐ左の項目がそのスペースと伸張文字のスペースを占めることを意味する．このようなシンボルにはSpanFromAboveとSpanFromBothがある．詳細は「WolframシステムのGrid，Row，Column」を参照のこと．
このアプローチは，複雑な伸張設定を生成するために使うことができる．入力として以下のようなものをタイプすると，長時間かかる．しかし挿入 ▶ 表・行列サブメニューの要素の結合と要素の分割を使うと，それをインタラクティブに生成することもできる．手で入植するにはどうすればよいかが見たい場合は，以下のセルを評価するとよい．
これまで，配列や背景を格子全体に，あるいは個々の列あるいは行に適用する方法を見てきた．しかし，各要素についてそれをどのようにオーバーライドするかということである．例えば，格子全体で数個の特別な要素を除いてすべてを同じ背景色にしたいとする．これを行う簡単な方法は，その特別な要素をItemでラップして，GridのオプションをオーバーライドするItemの対応するオプションを指定することである．
このオプションはStyleでオーバーライドすることもできる．しかしItemの目的はGridの二次元レイアウトについて分かっている方法でオーバーライドすることである．上の出力で分かるように，黄色いセルが2つ隣合せているとこにはその間のスペースに青は入っていない．これはItem以外のコンストラクトではできないことである．
これと同じことがBackgroundだけでなくItemのオプションすべてについて起る．Frameオプションを考えてみる．ある指定した要素以外には枠要素は必要ない場合，その要素を設定Frame->TrueのGridでラップするであろう（次のセクションでは，任意の式に枠を加えるずっと簡単な方法を紹介する）．
しかし，枠の付いた隣接する要素は境界線を同じくしない．これと以下のItemを使った例を比べてみる．後者は必要以上の沸く要素を描画しないという情報が十分にある．2と11の枠は1つの点を共有し，2と3の枠は1ピクセルの線を共有しており，この線が13と23の枠の左辺と完璧に揃っている．これがItemのパワーなのである．

枠とラベル

式に枠あるいはラベルを加えることはGridを使って行えるが，これは一般の二次元レイアウトよりもずっと単純な操作なのでもっと簡単に行うことができる．例えば，Framedは任意の式の周りに枠を描画するための簡単な関数である．これは，式の一部に注意事項を描画するとき等に便利である．
Labeledもそのような関数のひとつである．これは指定された式の周りの任意の位置にラベルを置くというものである．ここでは上のGridの例題に凡例を加える（Spacerは空のスペースを残しておくための関数である）．
Panelもまた枠のコンストラクトであり，オペレーティングシステムに内在するパネル枠を使用する．オペレーティングシステムによりパネル枠にドロップシャドウ，角丸，おしゃれなグラフィックデザイン等異なるものが使われているため，PanelはFrameとは異なる．
Panelにはフォントファミリおよびサイズに対して固有の概念があるため，Gridの内容でフォントファミリとサイズが変更され，Textでフォントサイズが変更される（Textにはフォントファミリについて独自の規定があるので，TextはWolframシステムのテキストフォントのままである）．これについては以下のBaseStyleオプションについてのセクションで触れる．
最後に述べておきたいのは，Panelでは1つ以上のラベルを指定するためのオプショナルの第2引数が取れるということである．このラベルは自動的にパネルの外側に置かれる．またオプショナルの第3引数ではその位置の詳細を指定することができる．詳細はPanelのドキュメントを参照するとよい．

その他の注釈

ここまでで見てきた注釈は，非常に明確な視覚的要素となっていた．しかし，ユーザが必要とするまで実質的に不可視となっている注釈も多数ある．例えば，Tooltipはその第1引数の表示は変更せず，その表示の上にマウスを置いたときだけ第2引数をツールチップとして表示する．
Mouseoverもそのような関数であるが，ツールチップで結果を表示する代りに，マウスポインタをその上に持ってくる前まで表示に使用されていたスクリーン上の同じ部分を使用する．2つの表示の大きさが異なる場合は，その効果が目障りなので，同じ大きさに近い表示を使うか，どちらが表示されているかにかかわらずそのうちの大きい方に十分なスペースを取るためのMouseoverのImageSizeオプションを使うかした方がよい．
Tooltipに似たものにStatusAreaとPopupWindowがある．StatusAreaではノートブックのステータスエリア（通常左下）に追加情報が表示され，PopupWindowはクリックすると新しいウィンドウに追加情報が表示される．
またAnnotationとMouseAnnotationを使うことで注釈の位置を指定することができる．
スクリーン上のある領域にマウスポインタを動かすことによってのみ表示される注釈を使うときは，ユーザのことを考えることが大切である．マウスを動かすことで長い評価が始まったり見にくくなったりしてはならない．注釈は慎重に使うとユーザにとって大変便利なものである．
これらの注釈はすべてグラフィックスの中でも十分に使用できる．生成した複雑なグラフィックスがユーザに理解してもらえるよう，ツールチップやマウスオーバーを提供することができる．実際，ListPlotやDensityPlot等の可視化関数でもTooltipをサポートする．詳細はドキュメントを参照するとよい．

デフォルトスタイル

「枠とラベル」のセクションで見たようにPanelのようなコンストラクトは，デフォルトのスタイルがこの内容に適用されるような環境を設定するという点で，Styleのように動作する．これは明示的なStyleコマンドでオーバーライドすることができるが，BaseStyleオプションを使いPanelでオーバーライドすることもできる．BaseStyleはStyleで使用するのと同じように，スタイルあるいはスタイル指示子のリストに設定する．するとこれらの指示子はそのPanelのスコープ内の環境デフォルトになる．
前述の通り，Panelはデフォルトでダイアログのフォントファミリとサイズを使う．しかしそれはこのBaseStyleオプションを使ってオーバーライドすることができる．
実際にこれらのボックスジェネレータのほとんどすべてにはBaseStyleオプションがある．例えば，デフォルトのフォントの色が青である格子があるとする．内側のStyleラッパーが外側のGrid BaseStyleに勝っているため，グレーの要素はグレーのままである（これはオプション継承の主な特徴のひとつであるが，これはこのドキュメントの範疇を超える）．

デフォルトオプション

仮にFramedやPanel等，同じボックス生成関数が何度も使ってある式があり，そのすべてが同じオプションを持つように変更したいとする．その関数が出てくるたびに同じオプションを加えていくのは面倒であるが，もっと簡単なやり方があるのである．
StyleのオプションであるDefaultOptionsは，形式 head->{opt->val,…}の要素のリストに設定されると，与えられたボックス生成頭部に対する全体的なデフォルトとして，指定されたオプションを持つ環境を設定する．これらのオプションはStyleラッパー全体で有効であるが，関連付けられたボックス生成関数の中でのみ有効である．
したがって，多数のFramed項目がある場合は，そのすべてが同じ背景および枠のスタイルを描画するようにしたい．
実は，上の入力は，このシンタックスの利点を見るには短かすぎる．同じリストを手動で指定したとすると以下のようになる．
FramedラッパーのそれぞれにオプションBackgroundとFrameStyleを挿入していくことは，できなくはない（あるいはそれを行うプログラムを書くこともできる）が非常に時間がかかる．しかしDefaultOptionsを使うと，すべてのFramedラッパーがBackgroundおよびFrameStyleに対する設定を使用するような環境が設定できる．
このアプローチにより，複数の場所でスタイルを指定する必要なく，一様なスタイルガイドラインに従う構造が簡単に生成できる．これだとコードも簡潔で，ファイルサイズも小さく管理が楽である．

数式のタイプセット

フォーマット出力を語る場合，数学的シンタックスに特有のフォーマットコンストラクトについて触れないわけにはいかない．
これらについて長々と説明はしないが，これらのコンストラクトにはカーネルにおいて組み込まれた数学的意味は持っていないということは言っておきたい．例えば，Superscript[a,b]はPower[a,b]と同様に表示されるが，この二つは同じものとは解釈されない．よって，表示に影響する意味を心配することなくフォーマット出力でこれらを構造要素として使うことができる．

ボックス言語の使用

すでにボックス言語をよくご存知の方は，これらのボックス生成関数が，低レベルボックスの構築およびそれらの出力の一部への挿入を妨害しているように思われることがあるかもしれない．これは一つの抽象化層がその下にある層を隠そうとするすべての層を使ったテクノロジーで起る．しかしこれには簡単な抜け穴があり，RawBoxesを使って有効だと分かっているボックスを取り，出力に直接表示することができるのである．
どの抜け穴でもそうであるように，RawBoxesで柔軟性が増すがそれで墓穴を掘ることもある．注意深く使わなければならない．まだボックス言語についてよく分かっていない場合は，使わない方がよい．
Wolfram言語のGrid，Row，Column

基本的コンストラクト

Wolfram言語は，スクリーンあるいはページ上に内容をレイアウトするための，後半に及ぶパワフルなコンストラクトを提供する．このコンストラクトは，初心者にとってもすぐに役立つものとして設計されており，しかも，あらゆる外観の部分に対しても細かい調整が可能である．

これらのコンストラクトは，タイプセット構造としてノートブック内に現れるコンストラクト，格子上に配列される内容を持つグラフィックスを生成する関数，フォーマットの詳細を調節するために格子内部に現れるコンストラクトの3つに分けることができる．

Grid，Column，RowはこのチュートリアルでGrid族と呼ぶ，最初のグループを形成する．Grid族を定義付ける特徴は，それがWolfram言語のタイプセットシステムと密接に統合された部分であるということである．つまり，どのような式であろうと内容として現れ，コンストラクト自身がウィンドウ幅あるいはその要素の大きさ等の変更に反応するということである．他のタイプセットコンストラクトと同様，Grid族のメンバは不活性なコンストラクトであり，評価されて別の形式になることはない．
これに匹敵するコンストラクトであるGraphics Grid族は，グラフィックスを扱う場合に特に便利な機能をサポートする．これらのコンストラクトはGraphicsGrid，GraphicsColumn，GraphicsRowである．グラフィックスはGrid族で使うことができるが，サイズ変更と編集をサポートするGraphics Grid族はよりグラフィックスに向いている．Graphics Grid族は引数を取り新しいグラフィックス式へと評価される関数である．このことは，生成された格子をその環境での変化に反応させることは難しいが，インタラクティブに任意の注釈を加えたり，グラフィックスを追加したりが簡単にできるということを意味する．
最後の族である埋め込まれたコンストラクト族は格子自身の中に埋め込まれているコンストラクトから構成され，その内部から格子の外観を変更する．Itemは格子の要素が現れる領域を表すためにその周りをラップする．SpanFromLeft，SpanFromAbove，SpanFromBothは複数の行や列に渡り伸張する領域を生成するために使われる．
これらすべてのコンストラクトの基本的な例を以下に挙げる．

Grid族

Grid[{{expr11,expr12,…},{expr21,expr22,…},…}]
二次元の格子に配列された exprij でフォーマットするオブジェクト
Column[{expr1,expr2,…}]
expr1 が expr2 の上，というように列に配列された expri でフォーマットするオブジェクト
Row[{expr1,expr2,…}]
数行に伸張する可能性のある行に配列された expri でフォーマットするオブジェクト
二次元フォーマットコンストラクトのGrid族
要素の格子：
要素の列：
要素の行：

Graphics Grid族

GraphicsGrid[{{g11,g12,…},…}]
gij が二次元格子にレイアウトされるようなグラフィックスを生成する
GraphicsColumn[{g1,g2,…}]
g1 が g2 の上というように，gi が列にレイアウトされるようなグラフィックスを生成する
GraphicsRow[{g1,g2,…}]
gi が行にレイアウトされるようなグラフィックスを生成する
二次元グラフィックスレイアウト関数のGraphics Grid族
グラフィックスの格子に要素を表示する：
グラフィックスの列に要素を表示する：
グラフィックスの行に要素を表示する：

埋め込まれたコンストラクト族

Item[expr,options]
expr を内容として，また，指定されたオプションを expr を含む領域に適用して表示する
SpanFromLeft
位置が左側の内容により占められていることを示す
SpanFromAbove
位置が上の内容により占められていることを示す
SpanFromBoth
位置が上と左の両方から占められていることを示す
GridおよびGraphics Grid族の中の要素として埋め込まれたときに特殊な意味を持つコンストラクト
要素"a"の周りにスタイル情報を埋め込む：
最初の2列に渡り"a"を伸張する：
最初の2行に渡り"a"を伸張する：
最初の2列と2行に渡り"a"を伸張する：

機能のクラス

Gridおよびその関連コンストラクトは，通常非常に少ないシンタックスでかなり外観をカスタマイズすることができる．下の表はサポートされる機能の種類を示している．詳細は後で説明する．

オプションのシンタックス

格子の外観の詳細を調整するために，多数のオプションが使える．このセクションでは，そのようなオプションの多くで共有される共通のシンタックスを説明する．このシンタックスは格子全体にオプション値を割り当てるだけでなく，個々の行，列，さらには項目にまでオプション値を割り当てる方法を提供する．

Background等，多くのオプションに対する全体的なシンタックスは，Background->{specx,specy}のような形式に基づく．ここで specx は各列に対する値を含むモジュラシンタックスであり，specy は各列に対する値を含む．

spec
spec をすべての項目に適用する
{specx}
specx を連続した水平の位置で適用する
{specx,specy}
speck を連続した水平および垂直の位置で適用する
{specx,specy,rules}
個々の i,j 要素に対する明示的な規則も許可する
一般的なオプションのシンタックス
specx と specy はどちらも，以下に説明する2つの形式を取ることができる．最初の形式は，指標の集合で所望の値に対する規則を与えるだけのものである．2つ目の形式は，値の列をリストで与えるということに基づいている．
列の指標とその背景色を指定する規則である：
上と等価である，連続した列に対して使用する背景色の値のリスト：

この2つのメソッドには，「規則の使用」および「リストの使用」に示すようにそれぞれ異なる利点がある．

規則の使用

規則は指定の行および列に指定の値を与えるという，直接的で判読可能なメソッドを提供する．

特定の列に背景色を設定する：
特定の行に背景色を設定する：

行数や列数が多いときは，規則を使うとそのいくつかに属性を設定するのに便利である．

可能な位置の中でわずかな数だけにオプションを適用する：

規則は，特定の格子要素や部分領域に値を与えるためにも使える．しかし，次に示すシンタックスは，概念的には同様でも specx および specy とは別のものである．

位置{3,3}で要素の背景色を設定する：
要素{1,1}から{3,3}までの領域に背景色を設定する：

規則は，規則の例外が存在する場合に，それが簡単に指定できる．しかし，格子のそれぞれの要素に手動で値を指定しようとしている場合は，それほど効率的とはいえない．

規則を使い，交互のパターンを手動で指定する：

反復パターンを作成するためには，代りに次のセクションで説明するリストシンタックスを使った方がよい．

リストの使用

リストで連続した値を与えることは，隣接行および列に対する多数のオプション値を指定するのに簡単で便利な方法である．

連続した列に対して使用する値をリストする：

また，値を循環的に使うことを表す部分リストを使うこともできる．

リストを循環的に使うよう指定する：

このような循環的な部分リストは，最初か最後で充填することができる．

循環部分の前に初期値の集合を与える：
値の最終値を与える：
中をデフォルトにする：

リストの位置は格子の位置に対応しているので，中ほどで単独の値を指定するためにはその前までの値をすべて与えなければならない．これをより直接的に行うためには，「規則の使用」で説明した規則を使う．

リストシンタックスを使い，5列目を赤にする：
背景色を直接割り当てるために規則を使う：

両方の使用

両方の長所を取り，格子の反復部分の指定にはリストシンタックスを，例外の指定には規則シンタックスを使うことができる．

最初と最後は赤にして，その他は青と緑を交互にした列：
最初と5番目の列以外はすべて青を使う：
{s1,s2,…,sn}
s1 から sn まで使う．その後はデフォルトを使う
{{c}}
すべての場合に c を使う
{{c1,c2}}
c1 と c2 を交互に使う
{{c1,c2,…}}
すべての ci を循環的に使う
{s,{c}}
s を使う．その後は c を反復的に使う
{s1,{c},sn}
s1を使う．その後は c を反復的に使い，最後に sn を使う
{s1,s2,…,{c1,
c2,…},
sm,…,
sn
}
最初に si の最初の列を使う．その後 ci を循環的に使用し，最後に si の最後の列を使う
{s1,s2,…,{},sm,…,sn}
最初に si の最初の列を使い，サイトに最後の列を使う
{i1->v1,i2->v2,…}
位置 ik で何を使うかを指定する
{spec,rules}
spec の指定をオーバーライドするために rules を使う
specx と specy のシンタックスのまとめ

列，行，溝，項目

前のセクションで紹介した通り，Wolfram言語は格子の部分に応じてオプション値を変更するための柔軟なシンタックスを提供する．このセクションでは，その言語のコンテキストを提供し，細かい違いを述べる．
格子の用語
column
項目の垂直の列
row
項目の水平の列
item
格子要素を含む領域
gutter
連続する行あるいは列の境界
二次元格子の各部分

GridおよびGraphicsGridは格子の各部分を記述する場合と同じ慣習に従う．Column，GraphicsColumn，GraphicsRowも同じ一般的な慣習に従うが，2つの可能な次元のうちのひとつだけしか扱わない．また，Rowはこのシステムには入らない．

オプションの名前

以下の表は，それぞれのオプションが対処することのできる部分を示したものである．すべてのコンストラクトに対してすべてのオプションが有効であるとは限らない．任意のコンストラクトに対して生じ得るオプションは以下の凡例を参照．

Rowはどのようなオプションも取らない．

列の次に行

オプションに対するシンタックスを覚えるときに，最も重要なステップは列に対する値をまず指定し，次に行に対する値を指定するということである．

opt->val
すべての項目に対して val を使う
opt->{colspec,rowspec}
列に colspec を，行に rowpec を使う
opt->{colspec}
列に colspec を，行にデフォルトを使う
GridおよびGraphicsGridに対するオプション構造

Wolfram言語では，水平設定 h，垂直設定 v のオプションは opt->{h,v}と指定する．この慣例が使われる代表的なオプションにImageSizeとPlotRangeがある．

格子では，これらの水平および垂直設定はそれぞれ列と行の値に対応する．これは，列は水平に重なっており，幅や位置等その他の属性も水平次元に対応しているためである．同様に行は垂直に重なっており，それらの属性は水平次元に対応している．

高さの2倍の幅のあるグラフィックスである：
下の格子では，項目の幅が2em，高さが1exである：
すべての列に同一の幅を使う代りに，各列に別の設定を与える：
連続する水平位置に異なる背景色を与えることもできる：

溝

多くのGridオプションは，最終的に列，行，または格子内の項目に関連付けることができる．

しかし，行と列の間の溝を扱うオプションもある．

Dividers
格子のどこに仕切り線を引くか
Spacings
水平および垂直のスペース
行と列の間の溝に対するオプション
どの行および列にも関連付けられていない線：
これと枠を比較してみる：

DividersとSpacingsのシンタックスは，他のオプションのシンタックスと全く同じである．特定の方向の n 項目の格子では，DividersとSpacingsは，最初の要素の前から始めて最後の要素の後で終わるようにして，要素間に n+1の隙間を指定することができる．

Items

最も細かい記述レベルはItemである．格子の中の各項目は，Background，Alignment，Frame等のオプションに対して，それぞれの値を持つことができる．

Itemは所望の設定を示すために明示的に使うことができる：
あるいは要素の {i,j} 指標を使い，全体的な格子レベルで値を割り当てることもできる：
プログラムで生成された格子：
格子の全領域に設定を与える：

仕切り線と枠

Wolfram言語は格子にどのような仕切り線と枠を描画するかを記述するための広範なシステムを提供する．
Dividers
列か行の間に仕切り線を描画する
Frame
格子の領域の周りに枠を描画する
FrameStyle
線に対して全体的なスタイルを使う
仕切り線と枠の描画のためのオプション
Frameを使い，領域あるいは領域の集合の4方すべてに線を引く：
特定の列あるいは行を強調する：

Frameは常に囲まれた領域の4方すべてに線を描画する．Dividersを使うとより細かく指定することができる．

仕切り線を使うときは，結果の線は1つの方向だけである．

中の仕切り線を描画する：

仕切り線と枠のスタイル

FrameStyleはFrameとDividersの両方に対して使われる基本スタイルを設定する：
FrameとDividersはどちらもスタイルを値として許す：
一般に，Hue，Thickness，Dashing，Dotted等を含むどのような線あるいは色の指示子を使うこともできる．複数の指示子はDirectiveで組み合せることができる．

優先

矛盾したスタイルが与えられると，DividersがFrameに優先する．またこれらはどちらもFrameStyleに優先する．Itemのスタイルは他のすべてに優先する．

仕切り線と枠は同時に加えることができる：
異なるソースからのスタイルは一緒にすることができる：

整列と位置

美しい格子には整列を必要とすることが多い．Wolfram言語では格子の整列方法を多数サポートしている．
Alignmentオプションはグリッド全体に渡すことができる．
内容を右に整列させる：
異なる列に対して異なる水平整列を，異なる行に対して異なる垂直整列を指定することができる．
最初の列を右に整列させ，2番目の列を左に整列させる：
格子の各項目に異なる整列を指定することができる．
位置{1,1}の要素を左に，位置{1,2}の要素を右に整列させる：
AlignmentはItemで設定することもできる．Itemの指定は優先される：
小数点，あるいは他の文字を整列させることができる．
"."で整列させる：
取り囲まれた環境の中で格子の位置を決めるにはBaselinePositionを使うとよい．
デフォルトの位置：
格子の下を周囲の式のベースラインに揃える：
{2,1}要素のベースラインが全体的なベースラインになるよう格子を整列させる：

背景とスタイル

一般的な場合

要素の集まりを扱う場合，Gridを使うとそれを一様な背景で設定することができる．

要素にはそれ自身の背景色があることもあるが，要素を並べただけでは不格好な隙間ができることがある．

Gridおよびその関連関数は，その要素を含むすべての項目全体に背景色を施す．

より高度なシンタックスを使うと，さまざまなパターンを作成することができる．

背景を交互にする：
交差する2つの行および列をハイライトする：
格子の内部に，特別な項目を持つ背景を埋め込む：

オーバーラップする背景設定の優先順位

以下のリストシンタックスで与えられる背景は交差する：
指標を使い，特に指定された背景が優先となる：
指標の付いた列は指標の付いた行に優先する：
Itemで指定された背景は最も優先順位が高い：

伸張とネスト

二次元空間の高度な分割は，ネストされた格子のコンストラクトおよび／または伸張要素の使用で実現できる．
名前の通り，伸張要素とは項目が複数の列，行，その両方に渡り伸びるものである．
"a"を最初の2列に渡り伸張させる：
"a"を最初の2行に渡り伸張させる：
"a"を最初の2行および2列に渡り伸張させる：
伸張領域は長方形でなければならない．長方形に収まらない項目は伸張させることができないため，伸張文字を表示する．
伸張は長方形でのみ可能である：
伸張要素を使うと多数のレイアウトが実現できるが，グリッドコンストラクトをネストしただけの方が速く簡単なことがある：
複雑な格子では特にそうであるが，特別に所望される構造を生成するためには，伸張の複雑なシステムを設計しようとするよりも，RowおよびColumnを使った方が簡単である．

サイズ変更とスペース

格子のサイズ変更

Gridは通常その要素の大きさを変更しない．また，行と列はデフォルトで内容が表示できるようできるだけ狭くなっている．

上の例では，2行目の方が1行目よりずっと高く，2列目の方が1列目よりも狭くなっており，要素の大きさは全く変更されていない．

もし格子の中の要素がインタラクティブに，または動的に変更されると，格子全体の大きさが適切に調整される．

例外として，Buttonはデフォルトで利用可能なスペースを満たすよう拡張する．

ItemSizeを使うとデフォルトの動作をオーバーライドすることができる．

すべての項目を同じ大きさにする：
個々の列と行に幅と高さを割り当てる：

ItemSize対して使われる単位は「ex」，「em」として知られるタイプセット単位である．

Scaledを使うと，囲んでいる領域の割合として幅を指定することもできる．

最初の2つの列をそれぞれページ幅の.3に指定する：
格子の中の改行

列が狭すぎる場合，テキスト的な項目は改行される．この場合行は指定の最小値よりも高くなる．

ItemSize->Automaticでは，テキスト項目はページ幅で改行される：
ItemSize->Fullでは，改行は禁止される：

GraphicsGridのサイズ変更

GraphicsGridはデフォルトで項目がすべて同じ大きさの格子を返す．

これは要素全体に対して適切な縦横比を自動的に選ぶ．

これとGridの例を比較してみると，後者は全体の大きさも縦横比も考慮しないことが分かる．

GraphicsGridはItemSizeオプションはサポートしないがImageSizeはサポートする．

ユーザからの入力
Wolfram言語の通常の動作では，ユーザにより入力される式が評価対象になる．しかし，プログラムの記述では，ユーザから段階的に入力を要求したい場合もある．そのようなときは，InputとInputStringの入力取込み機能が使える．
Input[]
入力されるものを式として取り込む
InputString[]
入力されるものを文字列として取り込む
Input["prompt"]
入力を求める旨を示したメッセージを表示した後，入力式を取り込む
InputString["prompt"]
入力を求める旨を示したメッセージを表示した後，入力文字列を取り込む
対話的な入力の取込み
InputとInputStringの動作はシステム動作環境や使っているWolfram言語のインターフェースにより違ってくる．テキスト型インターフェースを使っている場合は，通常，キーボードからの入力待ちになり，入力終了時に改行が実行される．一方，ノートブック型インターフェースの場合は，対話用の「ダイアログボックス」が表示されユーザからの入力が取り込まれる．
入力形態としては，Inputには自己完結型の式が入力可能であり，また，InputStringには任意の文字列が入力可能である．
メッセージ
計算時に発生するメッセージはすべて一般規定に基づいて処理される．組込み関数の多くがこの一般規定を使いエラーや警告用メッセージを生成している．ユーザ定義の関数についてもこの規定に基づいてメッセージを構築できるようになっている．
メッセージ構築の基本は，symbol::tag の形式でメッセージに固有の名前を与えることである．メッセージの参照はすべてこの名前を使う（symbol::tag はオブジェクトであり，その頭部はMessageNameになる）．
Quiet[expr]
メッセージを出力しないで expr を評価する
Quiet[expr,{s1::tag,s2::tag,…}]
指定されたメッセージを出力しないで expr を評価する
Off[s::tag]
メッセージの表示を禁止にする
On[s::tag]
メッセージを表示する
メッセージの表示制御
「警告とメッセージ」で説明したように，Quietを使って評価中の特定のメッセージの出力を制御することができる．組込み関数に関するメッセージの多くはデフォルトでオンの状態にある．メッセージを継続的に非表示にしたい場合は，Offを使うとよい．
式を入力すると，警告メッセージが表示される．また，フロントエンドは，余分は引数を赤でハイライトする：
警告メッセージを非表示にする：
メッセージは次の評価では再び表示されるようになる：
OnとOffを使うと，特定のメッセージの出力を大域的に変更することができる．メッセージが見たくない場合はOffを使う．
メッセージを表示禁止にするにはこのように命令しておく：
今度はメッセージは出ない：
組込み関数に関するメッセージの多くはデフォルトでオンの状態にあるが，メッセージによってはデフォルトでオフのものもある．それらはオンにしなければ表示されない．例としてGeneral::newsymのメッセージがある（詳細は「シンボル生成処理の内容確認」を参照のこと）．このメッセージは新規にメッセージが定義されると表示されるものである．
s::tag
メッセージの内容を表示する
s::tag=string
メッセージの内容文を名前に割り付ける
Messages[s]
式s に関連付けられているメッセージをすべて列記する
メッセージの基本操作
名前が s::tag であるメッセージ文は，シンボル s に関連した s::tag の「値」として保管される．メッセージ文を見るには s::tag と入力する．また，新たに s::tag に割り付けることで別のメッセージ内容を表示させることも可能である．
特異行列にLinearSolve関数を作用させる．すると警告メッセージが表示される：
このメッセージを参照してみる：
ユーザ定義のメッセージ文を割り付けてみる：
警告が出た式をまた入力する．今度は，ユーザ定義のメッセージが表示される：
メッセージ文はStringFormに対応した書式付きの文字列として記述される．あるイベントについてメッセージが出力されるとき，イベントを引き起した式が書式指定に従いメッセージ文に代入される．式自体はHoldFormがかけられ評価保留になる．また，StringFormで式が代入処理される前に，メッセージ表示の前処理関数指定の大域変数$MessagePrePrintに割り付けられている関数があれば式に適用される．$MessagePrePrintのデフォルトでは，テキストのフォーマットにはShortが，タイプセットにはShortとShallowの組合せが使われる．
メッセージのほとんどはそれを使う関数に密着した内容になっている．これに対して，特定の関数には直接関連付けされない「一般的な」メッセージもある．
関数 F に必要な数の引数を与えなかったら，F::argxに登録されている警告メッセージが表示される．もし F::argxに何も登録されていなければ，引数不正に関する「一般的な」メッセージ，General::argxが表示されることになっている．また，Off[F::argx]と入力しておけば，F に関する引数警告メッセージだけを表示禁止にできる．さらに，Off[General::argx]と入力しておくと，引数警告用の一般メッセージを表示禁止にする．
多すぎる引数を入力する．引数の数が不正という警告文が表示される：
引数の数が不正というメッセージは一般的なもので，実際，多くの関数で使われる：
Sqrt::argxにQuietを使うことでSqrt関数により発せられるメッセージを非表示にできるが，他の関数により発せられるものは非表示にはできない．
以下はSin::argxメッセージを出力するがSqrt::argxは出力しない：
General::argxを無効にすると，General::argxを使うメッセージすべてが表示されなくなる．
ここではargxメッセージが出力されない：
F::tag メッセージが General::tag を使っていないとき，General::tag を非表示にしても F::tag は非表示にならない．例えば，General::targメッセージを無効にしてもEntropy::targメッセージは無効にならない．それはこの2つのメッセージが同じものではないからである．
Entropy::targはGeneral::targと同じではない：
IdentityMatrix::targはGeneral::targと同じである：
Entropy::targメッセージはQuietの中でもまだ出力される：
計算処理がうまくいかないと，よく警告メッセージが何回も表示される．同じことを繰り返して表示してもあまり意味がないし，かえって，混乱させてしまうだろう．そこで，計算中に発生したメッセージはすべてWolfram言語内部に一時貯めこまれ，同じメッセージが3回連続して発生した場合，次からの表示が禁止になる．この事態が起ると，一般形メッセージGeneral::stopが表示されるようになっている．すべてのメッセージが見たい場合はGeneral::stopをオフにしておく．
$MessageList
最も最近の計算で発生した全メッセージのリスト
MessageList[n]
現行計算セッションの n 番目の入力式の評価処理において発生した全メッセージのリスト
計算セッションで発生したメッセージの再確認
Wolfram言語の内部には$MessageListの名前でリストスペースが確保され，計算が行われるたびに処理中に発生するメッセージがすべて記録される．標準設定の計算セッションでは，このリストは新たな出力行が生成された時点でクリアされてしまう．それでも，計算中にこのリストを参照することができる．また，n 番目の出力行が生成されるときには，最終メッセージリスト$MessageListの内容がコピーされMessageList[n]として別に保管される．
最終メッセージリスト($MessageList)の全内容を参照できるようにしておく：
メッセージの名前にはHoldFormがかけられているので，評価の対象にはならない：
計算プログラムを作っているときには，どんなメッセージであってもそれが生成されたかどうかを自動検出できることが重要になる．例えば，計算の結果，数値が確定不能になると，あるメッセージが発生する．その場合の計算結果は多分無意味なものだろう．
Check[expr,failexpr]
式 expr の評価でメッセージが発生しなかったら expr の評価結果を返し，そうでなければ式 failexpr を返す
Check[expr,failexpr,s1::t1,s2::t2,…]
指定メッセージ si::ti に限って自動検出する
警告メッセージの検出
1^0の計算では何もメッセージが発生しない．計算値がそのまま返ってくる：
0^0を計算させると，今度は，メッセージが表示され，Checkの第2引数が返される：
Check[expr,failexpr]の機能を使いメッセージ出力があったかどうか検出できる．ただし，Offで表示禁止になっているメッセージについては検出機能は働かない．
特定のメッセージに関してだけ自動検出した方が効果的になることがある．例えば，数値演算におけるオーバーフローのメッセージだけを検出したい場合がある．限定するにはCheckの引数に検出したいメッセージの名前を指定しておく．
Sin[1,2]の計算で発生するメッセージはCheckでは無視される．指定したメッセージではないからである：
Message[s::tag]
メッセージの内容文を表示する
Message[s::tag,expr1,…]
メッセージに式 expri を代入して構成した文を表示する
メッセージの表示
メッセージ関数Messageを使い組込み関数の行うメッセージ出力の詳細を再現することができる．例えば，OnとOff関数を使い関数のメッセージ表示をオン・オフし，もし，あるとき，メッセージ s::tag が表示禁止になっていたら，Messageが自動的に一般メッセージGeneral::tag を返してくれる．
fがオーバーフローを起したときに表示するメッセージの内容を定義しておく：
関数fを定義する：
fの引数が10より大きいのでオーバーフロー状態になり，メッセージが表示される：
メッセージ表示を禁止にしておく：
今度は，メッセージは現れない：
Messageの動作ステップとして，まず，指定した名前（頭部とタグ）のメッセージが検索される．見付からないときは，指定タグに関連した記号Generalのメッセージが検索される．それもない場合は，$NewMessageの大域変数に割り付けられている関数を参照し，指定頭部とタグを引数として同関数を適用する．
$NewMessageを適当に設定しておくことで，例えば，特定のメッセージについて，それがはじめて必要になったときにはファイルからメッセージ文を読み込むようにすることも可能である．
メッセージ：英語以外の言語への対応
標準版の組込み関数用メッセージは米国英語に対応した形で記述してある．Wolframシステムの言語別バージョンによっては英語以外の言語で記述したメッセージも提供されている．また，ユーザ定義のメッセージも英語以外の言語で記述できるようになっている．
言語指定は英語の言語名（文字列）で行われる．英語読みの名前が使われる理由は，特殊文字を必要としないためである．例えば，フランス語を指定するなら，"French"とする．
$Language="lang"
使用する言語を設定する
メッセージの言語環境の設定
フランス語に対応したメッセージ環境を設定しておく：
使用中のWolframシステムのバージョンがフランス語のメッセージを持つ場合，ここで生成されるメッセージはフランス語となる：
symbol::tag
メッセージ指定のデフォルト書式
symbol::tag::Language
特定言語で書かれたメッセージの指定書式
メッセージ指定のデフォルト書式と言語対応した書式
関数処理でメッセージ表示の要求があると，まず$Languageの言語指定が参照され，s::t::Language の言語別メッセージが検索される．見付からない場合は，s::t の標準英語メッセージが使われる．
組込み関数で取られる上記の検索ステップは，Messageを使い s::t のメッセージをユーザ定義の関数から表示するときにも使われる．ただし，メッセージ指定に言語を明示した場合は，その言語のメッセージしか検索されないので注意する．
説明文
Wolfram言語にはプログラムに説明を加えるための手法がいろいろ用意されている．しかし，プログラムを分かりやすくするという意味では，特別な説明を加えるより先に，使うオブジェクトに動作・作用が直ちに分かるような意味のある名前を付けるということがより重要だろう．
それでも，プログラムの機能や流れを分かりやすくするため説明を加えるとよい．これには，いわゆるコメント文を書き入れることになるが，式の記述と区別するため，説明文の文頭と末尾にカッコとアスタリスクの組合せ記号を加える．つまり，(* 説明文 *)というようにする．Wolfram言語では(* と *)で囲まれたコメント文はどのようにネストすることもできる．
式の途中にコメント文を入れても構わない：
(*text*)
コメント文はプログラムコードのどこに入れてもよい
コメント文の書式
プログラムを書く上での約束事として，関数を定義したら「使い方メッセージ」を設けておき，関数の基本機能等が参照できるようにしておく．関数に使い方メッセージを登録するには f::usageの名前に使い方を説明した文を割り付ける．メッセージを参照するには?f と入力する．
f::usage="text"
関数の使い方メッセージを定義する
?f
関数の使い方メッセージを参照する
??f
関数に関してより詳細な情報を得る
関数の使い方メッセージの定義と参照
関数fを定義する：
fの「使い方メッセージ」を作っておく：
fの使い方を調べてみる：
??fで詳細な情報を求める．fの定義式自体も見られる：
単に f の名前で関数定義だけをしたのなら，?f と入力すれば f の値が表示される．関数の使い方メッセージも定義してあれば，?f と入力すると使い方メッセージだけが表示される．また，??f と入力すれば，関数定義式を含む f に関する詳細な情報が表示される．
1つの関数に関して? で情報を検索するとその関数の使い方メッセージの全文が参照できる．メタキャラクタ等を使い複数の関数について情報の参照をした場合は，検索された関数名のみが，可能な場合は使用法メッセージへのリンクとともに表示される．
これは，Wolfram言語のシンボルの中で「Plot」で始まるものすべてである：
テキスト型インターフェースでは，メッセージとコメント文がプログラムに関する主要な情報源になる．ノートブック型インターフェースを使っている場合は，テキストセルの形で提供されるより詳細な説明が得られる．