データの数値処理
データの数値処理
| Mean[list] | 平均値 |
| Median[list] | メジアン(中央値) |
| Max[list] | 最大値 |
| Variance[list] | 分散 |
| StandardDeviation[list] | 標準偏差 |
| Quantile[list,q] | q に当たる分位数 |
| Total[list] | 総和 |
メジアンMedian[list]は,事実上,順序付けられたリスト list の中央の値を与える.これは値の広がりに依存する度合いが低いので,分布の中央を知るための平均よりも強力な尺度であると考えられることが多い.
しかし,分位数の定義で使われているものはこの他にも10種類程ある.そのすべてが多少異なった結果を与える.WolframシステムはQuantile[list,q,{{a,b},{c,d}}]の形式で4つの「分位数のパラメータ」を導入して一般的な事例をカバーする.パラメータ  と
と  は実際にリストのどの部分が
は実際にリストのどの部分が 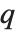 の位置であるかを定義する.これが整数の位置に当たるときにはその位置にある要素が
の位置であるかを定義する.これが整数の位置に当たるときにはその位置にある要素が 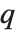 に当たる分位数とみなされる.これが整数の位置にないときには,
に当たる分位数とみなされる.これが整数の位置にないときには,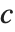 と
と 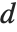 で定義されているようにどちらかの側の要素の線形結合が使われる.
で定義されているようにどちらかの側の要素の線形結合が使われる.
| {{0,0},{1,0}} | 実証的累積分布関数の逆関数(デフォルト) |
| {{0,0},{0,1}} | 線形補間法(カリフォルニア法) |
| {{1/2,0},{0,0}} | |
| {{1/2,0},{0,1}} | 線形補間法(水文学者法) |
| {{0,1},{0,1}} | 平均値に基づいた推定(ワイブル法) |
| {{1,-1},{0,1}} | 最頻値に基づいた推定 |
| {{1/3,1/3},{0,1}} | 中央値に基づいた推定 |
| {{3/8,1/4},{0,1}} | 標準分布推定 |
記述統計とは,位置,分散,形等の分布の特性を示すことである.ここで扱う関数はデータのリストの記述統計を計算する.「連続分布」および「離散分布」に含まれる関数を使うと,さまざまな既知の分布の標準的な記述統計のいくつかを計算することができる.
| Mean[data] | 平均値 |
| Median[data] | メジアン(中央値) |
| Commonest[data] | 最大頻度の要素のリスト |
| GeometricMean[data] | 幾何平均 |
| HarmonicMean[data] | 調和平均 |
| RootMeanSquare[data] | 二乗平均平方根 |
| TrimmedMean[data,f] | 並べ替えられたデータのリストの両端から割合 |
| TrimmedMean[data,{f1,f2}] | 並べ替えられたデータの両端からそれぞれ割合 |
| Quantile[data,q] | |
| Quartiles[data] | list の中の要素の |
位置の統計量とは,データがどこに位置するかを記述するものである.最も一般的な関数には平均,中央値,最頻値等,中心傾向を表すものがある.Quantile[data,q]はデータの下から パーセントに当たる点の位置を与える.つまり,Quantileは
パーセントに当たる点の位置を与える.つまり,Quantileは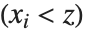 となる確率が
となる確率が 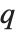 以下で,
以下で, となる確率が
となる確率が 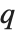 以上である値
以上である値 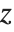 を与える.
を与える.
リストの最小要素を除外したときの平均である.TrimmedMeanを使うと,削除した外れ値を含むデータを記述することができる:
| Variance[data] | 分散の不偏推定量, |
| StandardDeviation[data] | 標準偏差の不偏推定量 |
| MeanDeviation[data] | 平均絶対偏差, |
| MedianDeviation[data] | 中央絶対偏差, |
| InterquartileRange[data] | 第1四分位数と第3四分位数との差 |
| QuartileDeviation[data] | 四分位偏差の半分 |
| Covariance[v1,v2] | リスト v1と v2の間の共分散係数 |
| Covariance[m] | 行列 m に対する共分散行列 |
| Covariance[m1,m2] | 行列 m1と m2に対する共分散行列 |
| Correlation[v1,v2] | リスト v1と v2の間の相関係数 |
| Correlation[m] | 行列 m に対する相関行列 |
| Correlation[m1,m2] | 行列 m1と m2に対する相関行列 |
共分散は分散の多変量拡張である.同じ長さの2つのベクトルの場合,共分散は数値である.単独の行列 m の場合は,共分散行列の i,j 番目の要素は,m の第 i 列と第 j 列の間の共分散である.2つの行列 m1と m2の場合は,共分散行列の i,j 番目の要素は,m1の第 i 列と m2の第 j 列の間の共分散である.
共分散は散らばりを測定し,相関は関連性を測定する.2つのベクトル間の相関は,そのベクトルの標準偏差で割ったベクトル間の共分散に等しい.同様に,相関行列の要素は,適切な列標準偏差でスケールされた対応する共分散行列の要素に等しい.
| CentralMoment[data,r] | r 次中心モーメント |
| Skewness[data] | 歪度係数 |
| Kurtosis[data] | 尖度係数 |
| QuartileSkewness[data] | 四分位の歪度係数 |
Skewnessは,三次中心モーメントを母集団の標準偏差の3乗で除算することで求められる.Kurtosisは,四次中心モーメントをデータの母分散の2乗で除算することで求められ,CentralMoment[data,2]と等価である(母分散は二次中心モーメント,母標準偏差はその平方根である).
| Expectation[f[x],xlist] | list の値についての x の関数 f の期待値 |
以下はデータのLogの期待値である:
ここで取り上げるのは,最も広く使われている一変量の離散分布であり,その密度,平均,分散,その他の関連特性を計算することができる.分布自体は name[param1,param2,…]という記号形式で表される.統計分布の特性を与えるMeanのような関数は,引数として分布の記号表現を取る.「連続分布」では多くの連続分布を説明している.
| BernoulliDistribution[p] | 平均 p のベルヌーイ(Bernoulli)分布 |
| BetaBinomialDistribution[α,β,n] | 成功確率がBetaDistribution[α,β]確率変数である二項分布 |
| BetaNegativeBinomialDistribution[α,β,n] | 成功確率がBetaDistribution[α,β]確率変数である負の二項分布 |
| BinomialDistribution[n,p] | 各試行における成功率を p としたときに,n 回の試行で起る成功回数の二項分布 |
| DiscreteUniformDistribution[{imin,imax}] | imin から imax までの整数上での離散一様分布 |
| GeometricDistribution[p] | 各試行における成功率を p としたときの,最初の成功までの試行回数の幾何分布 |
| HypergeometricDistribution[n,nsucc,ntot] | |
成功数 nsucc を含む大きさ ntot の母集団から標本数 n を取り出したときの成功数の超幾何分布 | |
| LogSeriesDistribution[θ] | パラメータ θ の対数級数分布 |
| NegativeBinomialDistribution[n,p] | パラメータ n および p の負の二項分布 |
| PoissonDistribution[μ] | 平均 μ のポアソン (Poisson) 分布 |
| ZipfDistribution[ρ] | パラメータ ρ のジップ(Zipf) 分布 |
正の整数 n に対する負の二項分布NegativeBinomialDistribution[n,p]とは,各試行における成功確率を p としたときに,n 回成功するまでに起った失敗回数の分布である.この分布は任意の正の n について定義される.しかし,n が整数でないときは,n が成功数,p が成功確率という解釈は当てはまらない.
ベータ二項分布BetaBinomialDistribution[α,β,n]は二項分布とベータ分布を組み合せたものである.BetaBinomialDistribution[α,β,n]の確率変数は,成功確率 p 自身がベータ分布BetaDistribution[α,β]に従う確率変数となっているBinomialDistribution[n,p]に従う.ベータ負の二項分布BetaNegativeBinomialDistribution[α,β,n]はベータ分布と負の二項分布を組み合せたものである.
超幾何分布HypergeometricDistribution[n,nsucc,ntot]は n 回の試行が,成功可能回数 nsucc 回でサイズ ntot の母集団から置換なしでサンプリングすることに相当する実験で,二項分布に代り使用されるものである.
ジップ(Zipf)分布ZipfDistribution[ρ]はゼータ分布と言われることがある.これは最初言語学で使われ,珍しい事象のモデル化にまで拡張された.
| PDF[dist,x] | x における確率密度関数 |
| CDF[dist,x] | x における累積分布関数 |
| InverseCDF[dist,q] | |
| Quantile[dist,q] | 第 q 分位数 |
| Mean[dist] | 平均 |
| Variance[dist] | 分散 |
| StandardDeviation[dist] | 標準偏差 |
| Skewness[dist] | 歪度係数 |
| Kurtosis[dist] | 尖度係数 |
| CharacteristicFunction[dist,t] | 特性関数 |
| Expectation[f[x],xdist] | dist に従って分布する x に対する f[x] の期待値 |
| Median[dist] | 中央値 |
| Quartiles[dist] | dist に対する |
| InterquartileRange[dist] | 第1四分位数と第3四分位数との差分 |
| QuartileDeviation[dist] | 四分位範囲の半分 |
| QuartileSkewness[dist] | 四分位数ベースの歪度 |
| RandomVariate[dist] | 指定された分布の擬似乱数 |
| RandomVariate[dist,dims] | 次元が dims で,指定された分布の要素を持つ擬似乱数配列 |
分布は記号形式で表現される.PDF[dist,x]は x が数値の場合は,x における密度関数を評価する.それ以外の場合は,可能な限り関数を記号形式のままにしておく.これと同様に,CDF[dist,x]は累積分布を与え,Mean[dist]は指定された分布の平均を与える.上の表は,分布で利用できる一般的な関数の例である.統計分布のさまざまな関数の詳説は,「連続分布」では,連続分布で対応するものを説明している.
ここに記載されている関数は,一変量の連続分布で最も一般的に使用されるものであり,連続分布の密度,平均,分散,その他の関連特性を計算することができる.分布は name[param1,param2,…]という記号形式で表現される.統計分布の特性を与えるMeanのような関数は,引数として分布の記号表現を取る.「離散分布」は多数の一般的な離散分布について記述する.
| NormalDistribution[μ,σ] | 平均 μ,標準偏差 σ の正規(ガウス)分布 |
| HalfNormalDistribution[θ] | 尺度がパラメータ θ に反比例する半正規分布 |
| LogNormalDistribution[μ,σ] | 平均 μ,標準偏差 σ の正規分布に基づいた対数正規分布 |
| InverseGaussianDistribution[μ,λ] | 平均 μ,尺度 λ の逆ガウス分布 |
対数正規分布LogNormalDistribution[μ,σ]は正規分布に基づく確率変数の指数関数が従う分布である.この分布は多数の独立確率変数が乗法的に統合された場合に起る.半正規分布HalfNormalDistribution[θ]は領域 に限られた分布NormalDistribution[0,1/(θ Sqrt[2/π])]に比例する
に限られた分布NormalDistribution[0,1/(θ Sqrt[2/π])]に比例する
逆ガウス分布InverseGaussianDistribution[μ,λ]はワルド(Wald)分布とも呼ばれ,正のドリフト付きブラウン運動の初期通過時間の分布である.
| ChiSquareDistribution[ν] | 自由度 ν の |
| InverseChiSquareDistribution[ν] | 自由度 ν の逆 |
| FRatioDistribution[n,m] | 分子の自由度が n,分母の自由度が m である |
| StudentTDistribution[ν] | 自由度が ν のスチューデントの t 分布 |
| NoncentralChiSquareDistribution[ν,λ] | 自由度が ν,非心パラメータが λ の非心 |
| NoncentralStudentTDistribution[ν,δ] | 自由度が ν,非心パラメータが δ の非心スチューデントの t 分布 |
| NoncentralFRatioDistribution[n,m,λ] | 分子の自由度が n,分母の自由度が m,非心パラメータが λ である非心 |
もし  が自由度
が自由度 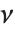 の
の 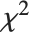 分布に従うならば,
分布に従うならば, は逆
は逆  分布InverseChiSquareDistribution[ν]に従う.自由度が
分布InverseChiSquareDistribution[ν]に従う.自由度が 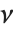 でスケールが
でスケールが 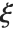 のスケールされた逆
のスケールされた逆 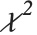 分布はInverseChiSquareDistribution[ν,ξ]として与えることができる.逆
分布はInverseChiSquareDistribution[ν,ξ]として与えることができる.逆 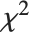 分布は,正規分布に従う標本のベイズ分析における分散の事前分布として広く使われている.
分布は,正規分布に従う標本のベイズ分析における分散の事前分布として広く使われている.
スチューデントの 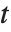 分布に従う変数は,正規確率変数の関数として書くこともできる.
分布に従う変数は,正規確率変数の関数として書くこともできる. と
と 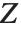 を独立した確率変数とする.ここで
を独立した確率変数とする.ここで  は標準的な正規分布,
は標準的な正規分布, 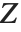 は自由度が
は自由度が 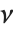 の
の  変数である.この場合,
変数である.この場合,  は自由度
は自由度 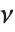 の
の 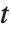 分布となる.スチューデントの
分布となる.スチューデントの 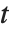 分布は縦軸について対称であり,標準偏差に対する正規変数の割合が特徴となっている.位置およびスケールのパラメータはStudentTDistribution[μ,σ,ν]の μ と σ として含めることができる.
分布は縦軸について対称であり,標準偏差に対する正規変数の割合が特徴となっている.位置およびスケールのパラメータはStudentTDistribution[μ,σ,ν]の μ と σ として含めることができる. のとき,
のとき,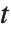 分布はコーシー分布と同じである.
分布はコーシー分布と同じである.
分散が  で平均が非零である正規分布に従う
で平均が非零である正規分布に従う 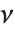 個の確率変数の平方和は,非心
個の確率変数の平方和は,非心 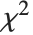 分布NoncentralChiSquareDistribution[ν,λ]に従う.非心パラメータ
分布NoncentralChiSquareDistribution[ν,λ]に従う.非心パラメータ  は総和における確率変数の平均の2乗和である.文献によっては,非心パラメータとして
は総和における確率変数の平均の2乗和である.文献によっては,非心パラメータとして 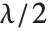 か
か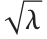 が使われることがある.
が使われることがある.
非心スチューデントの  分布NoncentralStudentTDistribution[ν,δ]は,比
分布NoncentralStudentTDistribution[ν,δ]は,比  を記述する.ここで
を記述する.ここで 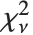 は自由度
は自由度 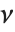 の
の 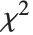 確率変数,
確率変数,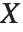 は分散
は分散  ,平均
,平均 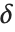 の正規分布の独立した確率変数である.
の正規分布の独立した確率変数である.
非心 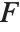 分布NoncentralFRatioDistribution[n,m,λ]は
分布NoncentralFRatioDistribution[n,m,λ]は  に対する
に対する 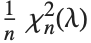 の比の分布である.ここで
の比の分布である.ここで  は非心パラメータ
は非心パラメータ  ,自由度
,自由度  の非心
の非心 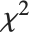 確率変数であり,
確率変数であり,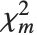 は自由度
は自由度 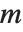 の
の  確率変数である.
確率変数である.
| TriangularDistribution[{a,b}] | 区間{a,b}での対称三角分布 |
| TriangularDistribution[{a,b},c] | c で最大となる区間{a,b}での三角分布 |
| UniformDistribution[{min,max}] | 区間{min,max}における一様分布 |
三角分布TriangularDistribution[{a,b},c]は 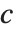 および
および 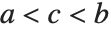 における最大確率内の
における最大確率内の 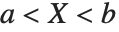 に対する三角分布である.
に対する三角分布である.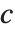 が
が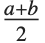 ならばTriangularDistribution[{a,b},c]は対称三角分布TriangularDistribution[{a,b}]である.
ならばTriangularDistribution[{a,b},c]は対称三角分布TriangularDistribution[{a,b}]である.
一様分布UniformDistribution[{min,max}]は, 矩形分布と呼ばれることもあり,値がどこにでも等しくあるような確率変数を特徴付ける.一様分布の確率変数の例には,min から max までの直線上でランダムに選んだ点の場所がある.
| BetaDistribution[α,β] | 形状パラメータが α と β の連続ベータ分布 |
| CauchyDistribution[a,b] | 位置パラメータが a,尺度パラメータが b のコーシー分布 |
| ChiDistribution[ν] | 自由度 ν の |
| ExponentialDistribution[λ] | 尺度がパラメータ λ に反比例する指数分布 |
| ExtremeValueDistribution[α,β] | 位置パラメータ α ,尺度パラメータ β の極値(Fisher-Tippett)分布 |
| GammaDistribution[α,β] | 形状パラメータ α,尺度パラメータ λ のガンマ分布 |
| GumbelDistribution[α,β] | 位置パラメータ α,尺度パラメータ β のガンベルの最小極値分布 |
| InverseGammaDistribution[α,β] | 形状パラメータ α,尺度パラメータ λ の逆ガンマ分布 |
| LaplaceDistribution[μ,β] | 平均 μ ,尺度パラメータ β のラプラス(二重指数)分布 |
| LevyDistribution[μ,σ] | 位置パラメータ μ,拡散パラメータ σ のレヴィ分布 |
| LogisticDistribution[μ,β] | 平均 μ,尺度パラメータ β のロジスティック分布 |
| MaxwellDistribution[σ] | 尺度パラメータ σ のマックスウェル(マックスウェル・ボルツマン)分布 |
| ParetoDistribution[k,α] | 最小値パラメータ k ,形状パラメータ α のパレート分布 |
| RayleighDistribution[σ] | 尺度パラメータ σ のレイリー(Rayleigh)分布 |
| WeibullDistribution[α,β] | 形状パラメータ α ,尺度パラメータ β のワイブル(Weibull)分布 |
もし確率変数  がガンマ分布GammaDistribution[α,β]に従うならば,
がガンマ分布GammaDistribution[α,β]に従うならば,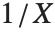 は逆ガンマ分布InverseGammaDistribution[α,1/β]に従う.確率変数
は逆ガンマ分布InverseGammaDistribution[α,1/β]に従う.確率変数 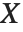 がInverseGammaDistribution[1/2,σ/2]に従うならば,
がInverseGammaDistribution[1/2,σ/2]に従うならば,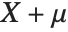 はラヴィ分布LevyDistribution[μ,σ]に従う.
はラヴィ分布LevyDistribution[μ,σ]に従う.
ラプラス (Laplace) 分布LaplaceDistribution[μ,β]は,同一の指数分布を持つ2つの独立した確率変数の差の分布である.ロジスティック分布LogisticDistribution[μ,β]は裾の長い分布を望む場合に,正規分布の代りに頻繁に使われる.
ワイブル (Weibull) 分布WeibullDistribution[α,β]は,物体の寿命を記述するために工学で広く使われている.極値分布ExtremeValueDistribution[α,β]は,正規分布を含む多様な分布から抽出された大きい標本における最大値に対する極限分布である.このような標本の最小値に対する極限分布は,ガンベル(Gumbel)分布GumbelDistribution[α,β]である.最大極値と最小極値は,変数の線形変化により関連しているので,極値分布とガンベル分布は同じ意味で使われることがある.また極値分布した確率変数と,適切にシフト・スケールされたワイブル分布した確率変数との間には対数関係があるので,極値分布は対数ワイブル分布と呼ばれることもある.
| PDF[dist,x] | x における確率密度関数 |
| CDF[dist,x] | x における累積分布関数 |
| InverseCDF[dist,q] | |
| Quantile[dist,q] | q 分位数 |
| Mean[dist] | 平均 |
| Variance[dist] | 分散 |
| StandardDeviation[dist] | 標準偏差 |
| Skewness[dist] | 歪度係数 |
| Kurtosis[dist] | 尖度係数 |
| CharacteristicFunction[dist,t] | 特性関数 |
| Expectation[f[x],xdist] | dist に従って分布する x に対する f[x]の期待値 |
| Median[dist] | 中央値 |
| Quartiles[dist] | dist に対する |
| InterquartileRange[dist] | 第1四分位数と第3四分位数の差分 |
| QuartileDeviation[dist] | 四分位範囲の半分 |
| QuartileSkewness[dist] | 四分位数ベースの歪度 |
| RandomVariate[dist] | 指定された分布を持つ擬似乱数 |
| RandomVariate[dist,dims] | 次元 dims で,指定された分布からの要素を持つ擬似乱数配列 |
逆累積分布関数InverseCDF[dist,q]はCDF[dist,x]が  に達するときの
に達するときの 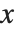 の値を返す.中央値はInverseCDF[dist,1/2]により与えられる.四分位数,十分位数,百分位数は,逆累積分布関数の特定の値である.四分位数の歪度は
の値を返す.中央値はInverseCDF[dist,1/2]により与えられる.四分位数,十分位数,百分位数は,逆累積分布関数の特定の値である.四分位数の歪度は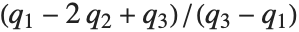 と等価であり,ここで
と等価であり,ここで 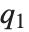 ,
,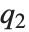 ,
, 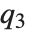 はそれぞれ第1,第2,第3の四分位数のことである.逆累積分布関数は統計パラメータの信頼区間を構築するときに使われる.InverseCDF[dist,q]とQuantile[dist,q]は連続分布については等価である.
はそれぞれ第1,第2,第3の四分位数のことである.逆累積分布関数は統計パラメータの信頼区間を構築するときに使われる.InverseCDF[dist,q]とQuantile[dist,q]は連続分布については等価である.
平均Mean[dist]は dist に従って分布した確率変数の期待値であり,通常 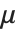 と表記される.平均は
と表記される.平均は 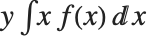 によって与えられる.ここで
によって与えられる.ここで 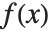 とは分布の確率密度関数である.分散Variance[dist]は
とは分布の確率密度関数である.分散Variance[dist]は  によって与えられる.分散の平方根は標準偏差と呼ばれ,通常
によって与えられる.分散の平方根は標準偏差と呼ばれ,通常  で表記される.
で表記される.
特性関数CharacteristicFunction[dist,t]は 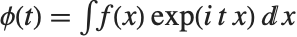 によって与えられる.離散の場合は,
によって与えられる.離散の場合は, となる.各分布にはそれぞれ固有の特性関数があり,分布を定義するために確率密度関数の代りに使用されることもある.
となる.各分布にはそれぞれ固有の特性関数があり,分布を定義するために確率密度関数の代りに使用されることもある.
RandomVariate[dist]は指定された分布から擬似乱数を与える.
これがその累積分布関数である.組込み関数のGammaRegularizedによって与えられる:
クラスタ分析とは,データの分類に使われる教師なし学習法である.データ要素は,距離(非類似度)関数に基づいたデータ要素の近似集団を表すクラスタと呼ばれるグループに分類される.ペアの要素が同一である場合は距離(非類似度)はゼロであり,それ以外のペアでは正となる.
| FindClusters[data] | data を類似要素のリストに分類する |
| FindClusters[data,n] | data を類似要素の最大 n 個のリストに分類する |
FindClustersのデータ引数はデータ要素のリスト,連想,要素とラベルにインデックスを付ける規則のいずれでもよい.
| {e1,e2,…} | データ要素 ei のリストとして指定されるデータ |
| {e1v1,e2v2,…} | データ要素 ei およびラベル vi の間の規則のリストとして指定されるデータ |
| {e1,e2,…}{v1,v2,…} | データ要素 ei およびラベル vi の間の規則のリストとして指定されるデータ |
| key1e1,key2e2…|> | 要素 ei をラベル keyi にマップする連想として指定されるデータ |
FindClustersでデータを指定する方法
FindClustersは数値データ,テキストデータ,画像データの他,ブールベクトル,日付,時間を含むさまざまなタイプのデータに使うことができる.すべてのデータ要素 ei は同じ次元でなければならない.
FindClustersは,数の近似に基づいてそれをクラスタ化する:
原則としては,任意次元で与えられた点をクラスタ化することは可能である.しかし,二次元,または三次元より大きい次元のクラスタを視覚化することは,できたとしても難しい.このドキュメントでは,選択可能なメソッドを比較するために,簡単に視覚化できる二次元データを使う.
FindClustersはデフォルト設定では点を4つのクラスタにした.
FindClustersの設定を変更して,クラスタの数を指定することもできる.
オプション名
|
デフォルト値
| |
| CriterionFunction | Automatic | 方法を選択する基準 |
| DistanceFunction | Automatic | 使用する距離(非類似度)尺度 |
| Method | Automatic | 使用するクラスタリング法 |
| PerformanceGoal | Automatic | 最適化する性能 |
| Weights | Automatic | 各例に与える重み |
FindClustersのオプション
FindClusters[{e1,e2,…},DistanceFunction->f]は,要素のペアの距離 f[ei,ej]が大きくなるにつれて,その類似度が減少するものとする.関数 f は,適切な距離(非類似度)関数であればどのようなものでもよい.距離関数 f は以下を満足する.
ei が数のベクトルであるなら,FindClustersではデフォルトでユークリッド平方距離が使われる.ei がブールのTrue ,False(あるいは0,1)要素のリストならば,FindClustersでは一致しない要素の正規化分数に基づく非類似度がデフォルトで使われる.ei が文字列の場合は,FindClustersでは1つの文字列から次を得るのに必要な点の変化の数に基づく距離関数がデフォルトで使われる.
| EuclideanDistance[u,v] | ユークリッド距離 |
| SquaredEuclideanDistance[u,v] | 平方ユークリッド距離 |
| ManhattanDistance[u,v] | マンハッタン距離 |
| ChessboardDistance[u,v] | チェス盤あるいはチェビシェフ距離 |
| CanberraDistance[u,v] | キャンベラ距離 |
| CosineDistance[u,v] | 余弦距離 |
| CorrelationDistance[u,v] | |
| BrayCurtisDistance[u,v] | ブレイ・カーティス距離 |
ブールベクトルの非類似度は,一般に2つのブールベクトル 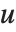 と
と 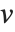 のペアの要素を比較することによって計算される.各非類似度関数は,
のペアの要素を比較することによって計算される.各非類似度関数は, を使って要約すると便利である.ここで
を使って要約すると便利である.ここで  は,それぞれ
は,それぞれ 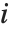 と
と 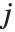 に等しい
に等しい  と
と 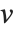 での対応する要素のペアの数である.数値
での対応する要素のペアの数である.数値 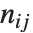 は
は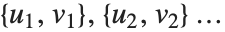 のペア
のペア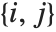 を数え,
を数え, と
と  は0か1のどちらかである.ブール値がTrueとFalseの場合,Trueは1と,Falseは0と等価である.
は0か1のどちらかである.ブール値がTrueとFalseの場合,Trueは1と,Falseは0と等価である.
| MatchingDissimilarity[u,v] | 単純なマッチ (n10+n01)/Length[u] |
| JaccardDissimilarity[u,v] | Jaccard係数 |
| RussellRaoDissimilarity[u,v] | Russell–Rao係数 (n10+n01+n00)/Length[u] |
| SokalSneathDissimilarity[u,v] | Sokal–Sneath係数 |
| RogersTanimotoDissimilarity[u,v] | Rogers–Tanimoto係数 |
| DiceDissimilarity[u,v] | Dice係数 |
| YuleDissimilarity[u,v] | Yule係数 |
| EditDistance[u,v] | 文字列 u を文字列 v に変換するための編集回数を計算する |
| DamerauLevenshteinDistance[u,v] | u と v の間のDamerau–Levenshtein距離 |
| HammingDistance[u,v] | u と v で値が一致しない要素の数 |
編集距離は,文字の順序を変えないで,1つの文字列を別の文字列に変換するのに必要な削除,挿入,代入の回数を数えることで決められる.これとは対照的に,Damerau–Levenshtein距離は削除,挿入,代入,転置の数を,ハミング距離は代入の数だけを数える.
異なるクラスタ方法を指定するためには,Methodオプションを使う.
| "Agglomerate" | 階層的クラスタリングを見付ける |
| "DBSCAN" | ノイズのあるアプリケーションの密度に基づいた空間クラスタリング |
| "GaussianMixture" | 変分ガウス混合アルゴリズム |
| "JarvisPatrick" | Jarvis–Patrickクラスタリングアルゴリズム |
| "KMeans" | k 平均クラスタリングアルゴリズム |
| "KMedoids" | メドイド分割 |
| "MeanShift" | 平均シフトクラスタリングアルゴリズム |
| "NeighborhoodContraction" | データ点を高密度の領域方向にシフトする |
| "SpanningTree" | 最小全域木ベースのクラスタリングアルゴリズム |
| "Spectral" | スペクトラルクラスタリングのアルゴリズム |
Methodオプションの明示的設定
デフォルトではFindClustersは異なるメソッドを試し,最もよいクラスタリングを選ぶ.
メソッド"DBSCAN","JarvisPatrick","MeanShift","SpanningTree","NeighborhoodContraction","GaussianMixture"は,特定のクラスタ数を想定しないで,どのようにデータをクラスタ化するかを決定する.
| "NeighborhoodRadius" | 点の近傍の平均半径を指定する |
| "NeighborsNumber" | 近傍における点の平均個数を指定する |
| "InitialCentroids" | 最初の重心,medoidを指定する |
| "SharedNeighborsNumber" | 共有される近傍の最低数を指定する |
| "MaxEdgeLength" | 長さをせん定する閾値を指定する |
| ClusterDissimilarityFunction | クラスタ間非類似度を指定する |
サブオプション"NeighborhoodRadius"は,メソッド"DBSCAN","MeanShift","JarvisPatrick","NeighborhoodContraction","Spectral"で使うことができる.
"InitialCentroids"サブオプションは"KMeans"メソッドおよび"KMedoids"メソッドの最初の設定を変更するために使うことができる.初期設定が適切でないと,クラスタリングの結果もよくならない.
| "Single" | 最短距離法 |
| "Average" | 群平均法 |
| "Complete" | 最長距離法 |
| "WeightedAverage" | 重み付き群平均法 |
| "Centroid" | クラスタの重心からの距離 |
| "Median" | クラスタのメジアンからの距離 |
| "Ward" |
ウォード(Ward)の最小分散法
|
| f | 純関数 |
ClusterDissimilarityFunction->f では,f は連結法を定義する純関数である.クラスタ間の距離(非類似度)は,新しく融合するクラスタの距離(非類似度)を決定するために,融合していないクラスタ間の距離(非類似度)についての情報を使い,ことにより,再帰的に決められる.関数 f はクラスタ k からクラスタ i と j を融合して形成された新しいクラスタまでの距離を定義する.f に与えられる引数は dik,djk,dij,ni,nj,nk であり,d はクラスタ間の距離,n はクラスタ内の要素数である.
CriterionFunctionオプションは使用するメソッドとクラスタの最適数の両方を選ぶために使うことができる.
| "StandardDeviation" | 二乗平均平方根の標準偏差 |
| "RSquared" | R二乗 |
| "Dunn" | Dunn指標 |
| "CalinskiHarabasz" | Calinski–Harabasz指標 |
| "DaviesBouldin" | Davies–Bouldin指標 |
| Automatic | 内部指標 |
次はCriterionFunctionに異なる設定を使った,クラスタリングの結果を示す:
以下は,デフォルトのCriterionFunctionと,自動的に選ばれたクラスタ数を使って見付かったクラスタである:
Nearestは,指定されたデータ点に最も近いリスト中の要素を見付けるために使う.
| Nearest[{elem1,elem2,…},x] | x が最も近い elemi のリストを与える |
| Nearest[{elem1->v1,elem2->v2,…},x] | |
x が最も近い elemi に対応する vi を与える | |
| Nearest[{elem1,elem2,…}->{v1,v2,…},x] | |
同じ結果を与える | |
| Nearest[{elem1,elem2,…}->Automatic,x] | |
vi を整数1, 2, 3, …として取る | |
| Nearest[data,x,n] | x に近い n 個の要素を与える |
| Nearest[data,x,{n,r}] | 半径 r 内で x に最も近い要素を最大 n 個与える |
| Nearest[data] | 異なる x に繰り返し適用できるNearestFunction[…]を生成する |
Nearest関数
Nearestは数値のリスト,テンソル,文字列のリストに使える.
次で2Dにおける10,000個の点の集合とNearestFunctionを生成する:
NearestFunctionを使わなかったら,もっと時間がかかる:
オプション名
|
デフォルト値
| |
| DistanceFunction | Automatic | 使用する距離測定法 |
Nearestのオプション
| Fit[{y1,y2,…},{f1
,
f2,…},x] | 値 yn を関数 fi の線形結合にフィットする |
| Fit[{{x1,y1},{x2,y2},…},{f1
,
f2,…},x] | 点(xn,yn)を fi の線形結合にフィットする |
| FindFit[data,form,{p1,p2,…},x] | パラメータ pi を含む form に対するフィットを求める |
| Fourier[data] | 数値フーリエ変換 |
| InverseFourier[data] | 逆フーリエ変換 |
Wolfram言語のフーリエ変換関数Fourierは,理学でよく使われる符号表記に従った形で定義されている.電気工学でよく使われる表記とは逆であることに注意されたい.詳しい説明は「離散フーリエ変換」を参照のこと.
与えられたデータセットに最も適した式を求めたいことがある.Wolfram言語でこれを行う方法のひとつはFitを使うことである.
| Fit[{f1,f2,…},{fun1,fun2,…},x] | 値 fi に最もフィットするの線形結合 funi を求める |
| {f1,f2,…} | |
| {{x1,f1},{x2,f2},…} | |
| {{x1,y1,…,f1},{x2,y2,…,f2},…} | 座標の列 |
Fitは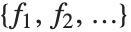 形式のデータが与えられると連続する
形式のデータが与えられると連続する  が連続する整数点
が連続する整数点 における関数の値に当たると仮定する.Fitには関数の任意の点における値に相当するデータを与えることもできる.次元は一次元でも多次元でもよい.
における関数の値に当たると仮定する.Fitには関数の任意の点における値に相当するデータを与えることもできる.次元は一次元でも多次元でもよい.
| Fit[data,{fun1,fun2,…},{x,y,…}] | 複数の変数を持つ関数にフィットする |
Fitは関数のリストを取り,明確で効果的な手順でこれらの関数のどのような線形結合がデータの最高の最小2乗フィットを与えるかを求める.しかし,指定の関数の線形結合だけからなるのではない「非線形フィット」を求めたいこともあるだろう.その場合はFindFitを使うとよい.この関数はいかなる形の関数でも取り,データに最適のフィットを与えるパラメータの値を求める.
| FindFit[data,form,{par1,par2,…},x] | form が data に最もフィットする pari の値を求める |
| FindFit[data,form,pars,{x,y,…}] | 多変量データのフィット |
結果はFitによるものと同じである:
これはFitでは扱えない非線形形式をフィットする:
デフォルトにより,FitとFindFitは両方とも「最小二乗」フィットを生み出す.これは  を最小化すると定義することができる.ここで
を最小化すると定義することができる.ここで 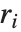 はオリジナルの各データ点とフィットした値の差分を与える残差である.これとは別のノルムに基づいたフィットを考えることもできる.オプションNormFunction->u を設定するとFindFitは u[r]を最小にするフィットを求めようとする.ここで r は残差のリストである.デフォルトはNormFunction->Normで最小二乗フィットに対応している.
はオリジナルの各データ点とフィットした値の差分を与える残差である.これとは別のノルムに基づいたフィットを考えることもできる.オプションNormFunction->u を設定するとFindFitは u[r]を最小にするフィットを求めようとする.ここで r は残差のリストである.デフォルトはNormFunction->Normで最小二乗フィットに対応している.
FindFitは最適なフィットを与えるパラメータの値を求めるという形を取る.検索を始める点を指定しなければならないこともある.この指定は の形式でパラメータを与えることで行う.FindFitには検索方法をコントロールするためのたくさんのオプションがある.
の形式でパラメータを与えることで行う.FindFitには検索方法をコントロールするためのたくさんのオプションがある.
オプション名
|
デフォルト値
| |
| NormFunction | Norm | 使用するノルム |
| AccuracyGoal | Automatic | 確度の目標桁数 |
| PrecisionGoal | Automatic | 精度の目標桁数 |
| WorkingPrecision | Automatic | 内部計算精度 |
| MaxIterations | Automatic | 最大反復回数 |
| StepMonitor | None | 段階を踏むたびに常に評価される式 |
| EvaluationMonitor | None | form が評価されたときに常に評価される式 |
| Method | Automatic | 使用するアルゴリズム |
FindFitのオプション
モデルをデータにフィットさせるとき,そのモデルがいかによくデータにフィットしているか,またそのフィットがモデルの仮定にどの程度一致しているかを解析すると便利なことがよくある.Wolframシステムでは,一般の統計モデルの多くでFittedModelオブジェクトを構築するフィット関数によりこれが実現できる.
| FittedModel | 記号的にフィットされたモデルを表す |
FittedModelオブジェクトはある時点で評価することも,結果や診断情報を問い合わせることもできる.診断はモデルの型により多少異なる.利用できるモデルフィット関数は,線形,一般化された線形,非線形の各モデルにフィットする.
| LinearModelFit | 線形モデルを構築する |
| GeneralizedLinearModelFit | 一般化された線形モデルを構築する |
| LogitModelFit | 二項ロジスティック回帰モデルを構築する |
| ProbitModelFit | 二項プロビット回帰モデルを構築する |
| NonlinearModelFit | 非線形最小二乗モデルを構築する |
FittedModelオブジェクトを生成する関数
LinearModelFit等のモデルフィット関数とFitやFindFit等の関数との大きな違いは,診断情報をFittedModelオブジェクトからいかに簡単に取得できるかという点にある.この結果はモデルを再フィットしなくてもアクセスできる.
プロパティの計算に関係するフィットのオプションは,FittedModelオブジェクトに渡され,デフォルトがオーバーライドされる.
線形モデル
独立正規分布に従う誤差を仮定した線形モデルは,データのモデルで最も一般的なもののひとつである.このタイプのモデルはLinearModelFit関数を用いてフィットすることができる.
| LinearModelFit[{y1,y2,…},{f1,f2,…},x] | 基底関数が fi,単独の予測変数が x である線形モデルを得る |
| LinearModelFit[{{x11,x12,…,y1},{x21,x22,…,y2}},{f1,f2,…},{x1,x2,…}] | 複数の予測変数が xi である線形モデルを得る |
| LinearModelFit[{m,v}] | 計画行列 m と応答ベクトル v に基づく線形モデルを得る |
線形モデルの形式は 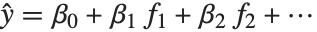 であり,
であり, はフィットあるいは予測された値,
はフィットあるいは予測された値, はフィットされるためのパラメータ,
はフィットされるためのパラメータ,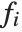 は予測変数
は予測変数 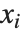 の関数を表す.モデルはパラメータ
の関数を表す.モデルはパラメータ  において線形である.
において線形である. は予測変数のいかなる関数でもよい.
は予測変数のいかなる関数でもよい.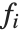 は単に予測変数
は単に予測変数 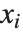 となることが多い.
となることが多い.
オプション名
|
デフォルト値
| |
| ConfidenceLevel | 95/100 | パラメータおよび予測に使う信頼水準 |
| IncludeConstantBasis | True | 一定の基底関数を含むかどうか |
| LinearOffsetFunction | None | 線形予測子における既知のオフセット |
| NominalVariables | None | 名義あるいはカテゴリと考えられる変数 |
| VarianceEstimatorFunction | Automatic | 誤差分散を推定するための関数 |
| Weights | Automatic | データ要素の重み |
| WorkingPrecision | Automatic | 内部計算で使用する精度 |
LinearModelFitのオプション
Weightsオプションは重み付きの線形回帰に対する重みの値を指定する.NominalVariablesオプションはどの予測変数を名義あるいはカテゴリ変数として扱うかを指定する.NominalVariables->Allの設定では,モデルは分散分析(ANOVA)モデルである.NominalVariables->{x1,…,xi-1,xi+1,…,xn}では,モデルは共分散分析(ANCOVA)モデルで 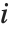 番目の予測子以外はすべて名義変数として扱われる.名義変数は二値変数の集まりで表され,その変数の観察された名義カテゴリ変数の等式および不等式を示す.
番目の予測子以外はすべて名義変数として扱われる.名義変数は二値変数の集まりで表され,その変数の観察された名義カテゴリ変数の等式および不等式を示す.
ConfidenceLevel,VarianceEstimatorFunction,WorkingPrecisionは最初のフィットの後の結果の計算に関係している.これらのオプションはLinearModelFit内部で設定することができ,FittedModelオブジェクトから得られた結果のデフォルト設定を指定する.また,すでに構築されたFittedModelオブジェクトの内部で設定し,最初にLinearModelFitに与えられたオプション値をオーバーライドすることもできる.
IncludeConstantBasis,LinearOffsetFunction,NominalVariables,Weightsはフィットにだけ関係する.すでに構築されているFittedModelオブジェクト内でこれらのオプションを設定しても結果には何の影響もない.
| "BasisFunctions" | 基底関数のリスト |
| "BestFit" | フィットされた関数 |
| "BestFitParameters" | パラメータ推定 |
| "Data" | 入力データあるいは計画行列と応答ベクトル |
| "DesignMatrix" | モデルに対する計画行列 |
| "Function" | 一番よいフィットの純関数 |
| "Response" | 入力データの応答値 |
"BestFitParameters"プロパティはフィットされたパラメータ値{β0,β1,…}を与える."BestFit"はフィットされた関数  であり,"Function"はフィットされた関数を純関数として与える."BasisFunctions"は,定数項がモデルに存在する場合に
であり,"Function"はフィットされた関数を純関数として与える."BasisFunctions"は,定数項がモデルに存在する場合に 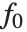 を定数1とした関数
を定数1とした関数 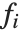 のリストを与える."DesignMatrix"はデータの計画行列またはモデル行列である."Response"は応答のリスト,あるいはもとのデータからの
のリストを与える."DesignMatrix"はデータの計画行列またはモデル行列である."Response"は応答のリスト,あるいはもとのデータからの 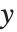 値を与える.
値を与える.
| "FitResiduals" | 実際応答と予測応答の差 |
| "StandardizedResiduals" | 各残差について標準誤差で割られた残差 |
| "StudentizedResiduals" | 単一の削除誤差推定で割られた残差 |
残差はフィットされた値ともとの応答との点による差分を測定する."FitResiduals"は観察された値とフィットされた値の差分{y1-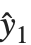 ,y2-
,y2-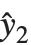 ,…}を与える."StandardizedResiduals"および"StudentizedResiduals"は残差のスケールされた形式である.
,…}を与える."StandardizedResiduals"および"StudentizedResiduals"は残差のスケールされた形式である.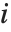 番目の標準化された残差は
番目の標準化された残差は  である.ここで
である.ここで  は推定誤差分散,
は推定誤差分散,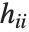 はハット行列の
はハット行列の 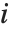 番目の対角要素,
番目の対角要素,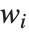 は
は  番目のデータ点の重みである.
番目のデータ点の重みである. 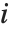 番目のスチューデント化された残差も同じ式で,
番目のスチューデント化された残差も同じ式で,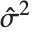 を
を 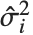 (
(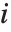 番目のデータ点を省略した分散推定)で置き換えたものである.
番目のデータ点を省略した分散推定)で置き換えたものである.
| "ANOVATable" | 分散分析表 |
| "ANOVATableDegreesOfFreedom" | ANOVA表からの自由度 |
| "ANOVATableEntries" | 表からのフォーマットされていない配列の値 |
| "ANOVATableFStatistics" | 表からのF統計量 |
| "ANOVATableMeanSquares" | 表からの平方平均誤差 |
| "ANOVATablePValues" | 表からの |
| "ANOVATableSumsOfSquares" | 表からの平方和 |
| "CoefficientOfVariation" | 推定標準偏差で割られた応答平均 |
| "EstimatedVariance" | 誤差分散の推定 |
| "PartialSumOfSquares" | 非定数基底関数が除去されたときのモデル平方和の変化 |
| "SequentialSumOfSquares" | 要素ごとに区切られたモデル平方和 |
"ANOVATable"はモデルに対するフォーマットされた分散分析表を与える."ANOVATableEntries"は表の中の数値的項目を与える.その他のANOVATableプロパティは,表の中の個々の部分が今後の計算で簡単に使えるように表の列の要素を与える.
| "CorrelationMatrix" | パラメータ相関行列 |
| "CovarianceMatrix" | パラメータ共分散行列 |
| "EigenstructureTable" | パラメータ相関行列の固有構造 |
| "EigenstructureTableEigenvalues" | 表からの固有値 |
| "EigenstructureTableEntries" | 表からのフォーマットされていない値の配列 |
| "EigenstructureTableIndexes" | 表からの指標値 |
| "EigenstructureTablePartitions" | 表からの区分 |
| "ParameterConfidenceIntervals" | パラメータ信頼区間 |
| "ParameterConfidenceIntervalTable" | フィットされたパラメータの信頼区間情報の表 |
| "ParameterConfidenceIntervalTableEntries" | 表からのフォーマットされていない値の配列 |
| "ParameterConfidenceRegion" | 楕円体パラメータ信頼領域 |
| "ParameterErrors" | パラメータ推定の標準誤差 |
| "ParameterPValues" | パラメータの |
| "ParameterTable" | フィットされたパラメータ情報の表 |
| "ParameterTableEntries" | 表からのフォーマットされていない値の配列 |
| "ParameterTStatistics" | パラメータ推定の |
| "VarianceInflationFactors" | 推定パラメータの拡大要因のリスト |
"CovarianceMatrix"はフィットされたパラメータ間の共分散を与える.その行列は  であり,ここで
であり,ここで 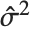 は分散推定,
は分散推定,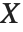 は計画行列,
は計画行列, は重みの対角行列である."CorrelationMatrix"はパラメータ推定に対して関連付けられた相関行列である."ParameterErrors"は共分散行列の対角要素の平方根に等しい.
は重みの対角行列である."CorrelationMatrix"はパラメータ推定に対して関連付けられた相関行列である."ParameterErrors"は共分散行列の対角要素の平方根に等しい.
上記の表のEstimateの列は"BestFitParameters"に等しい.t 統計は推定を標準誤差で割ったものである.それぞれの p 値は,t 統計に対しては両側 p 値であり,パラメータ推定が統計的に0と有意差があるかどうかを判定するために使われる.それぞれの信頼区間はConfidenceLevelオプションにより設定された水準で,パラメータ信頼区間の上限と下限を与える.表の列やフォーマットされていない値の配列を得るために,ParameterTableおよびParameterConfidenceIntervalTableのさまざまなプロパティが使える.
"VarianceInflationFactors"は基底関数間の多重共線性を測定するために使われる.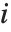 番目の拡大要因は
番目の拡大要因は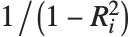 に等しい.ここで
に等しい.ここで 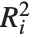 は
は  番目の基底関数を別の基底関数の線形関数にフィットすることからの変動係数である.IncludeConstantBasis->Trueの設定では,最初の拡大要因は定数項に対するものとなる.
番目の基底関数を別の基底関数の線形関数にフィットすることからの変動係数である.IncludeConstantBasis->Trueの設定では,最初の拡大要因は定数項に対するものとなる.
"EigenstructureTable"は固有値,条件指標,非定数基底関数に対する分散分割を与える.Indexの列は最大固有値に対する固有値の比の平方根である.それぞれの基底関数の列は,関連付けられた固有ベクトルにより説明される基底関数における変動の割合である."EigenstructureTablePartitions"は表におけるすべての基底関数に対する変動分割の値を与える.
| "BetaDifferences" | パラメータ値の影響のDFBETAS尺度 |
| "CatcherMatrix" | キャッチャー行列 |
| "CookDistances" |
クック(Cook)の距離のリスト
|
| "CovarianceRatios" | 観察影響のCOVRATIO尺度 |
| "DurbinWatsonD" | 自己相関のダービン・ワトソン(Durbin–Watson) |
| "FitDifferences" | 予測値に対する影響のDFFITS尺度 |
| "FVarianceRatios" | 観察影響のFVARATIO尺度 |
| "HatDiagonal" | ハット行列の対角要素 |
| "SingleDeletionVariances" |
点の規模での影響の測定は,各データ点がフィットに大きい影響を与えるかどうかを評価するために使われることがよくある.ハット行列とキャッチャー行列はそのような診断で重要な役割を果たす.ハット行列は  となるような行列
となるような行列 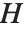 であり,ここで
であり,ここで 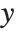 は観察された応答ベクトル,
は観察された応答ベクトル, は予測された応答ベクトルである."HatDiagonal"はハット行列の対角要素を与える."CatcherMatrix"は
は予測された応答ベクトルである."HatDiagonal"はハット行列の対角要素を与える."CatcherMatrix"は  (ここで
(ここで  はフィットしたパラメータベクトル)となるような行列
はフィットしたパラメータベクトル)となるような行列  である.
である.
"FitDifferences"はそれぞれのデータ点がフィットされた値または予測された値に及ぼす値を測定するDFFITS値を与える. 番目のDFFITS値は
番目のDFFITS値は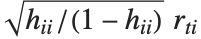 で記述される.ここで
で記述される.ここで 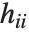 は
は 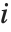 番目のハット対角要素であり,
番目のハット対角要素であり,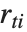 は
は 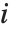 番目のスチューデント化された残差である.
番目のスチューデント化された残差である.
"BetaDifferences"はそれぞれのデータ点がモデルのパラメータに及ぼす影響を測定するDFBETAS値を与える. 個のパラメータを持つモデルの場合,"BetaDifferences"の
個のパラメータを持つモデルの場合,"BetaDifferences"の  番目の要素は長さ
番目の要素は長さ 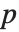 のリストであり,
のリストであり,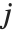 番目の値がデータ点
番目の値がデータ点 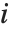 がモデルの中の
がモデルの中の 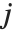 番目のパラメータに及ぼす影響を測定する.
番目のパラメータに及ぼす影響を測定する.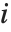 番目の"BetaDifferences"ベクトルは
番目の"BetaDifferences"ベクトルは  と書くことができ,ここで
と書くことができ,ここで 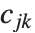 はキャッチャー行列の
はキャッチャー行列の 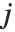 ,
, 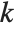 番目の要素を表す.
番目の要素を表す.
| "MeanPredictionBands" | 平均予測の信頼帯 |
| "MeanPredictionConfidenceIntervals" | 平均予測の信頼区間 |
| "MeanPredictionConfidenceIntervalTable" | 平均予測の信頼区間表 |
| "MeanPredictionConfidenceIntervalTableEntries" | 表からのフォーマットされていない値の配列 |
| "MeanPredictionErrors" | 平均予測の標準誤差 |
| "PredictedResponse" | データのフィットされた値 |
| "SinglePredictionBands" | 1回の観察に基づいた信頼帯 |
| "SinglePredictionConfidenceIntervals" | 1回の観察の予想される応答の信頼区間 |
| "SinglePredictionConfidenceIntervalTable" | 1回の観察の予想される応答の信頼区間の表 |
| "SinglePredictionConfidenceIntervalTableEntries" | 表からのフォーマットされていない値の配列 |
| "SinglePredictionErrors" | 1回の観察の予測応答の標準誤差 |
信頼区間の表形式の結果は"MeanPredictionConfidenceIntervalTable"および"SinglePredictionConfidenceIntervalTable"で与えられる.これには観測された応答と予測された応答,標準誤差推定,各点に対する信頼区間が含まれる.平均の予測信頼区間は単に信頼区間と言われ,単独の予測信頼区間は予測区間と言われることが多い.
平均の予測区間は,予測子の固定値における応答  の平均の信頼区間を与えるものであり,
の平均の信頼区間を与えるものであり, により与えられる.ここで
により与えられる.ここで  は,自由度
は,自由度  のスチューデントの
のスチューデントの 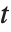 分布の
分布の 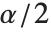 分位数,
分位数, は固定された予測子で評価された基底関数のベクトル,
は固定された予測子で評価された基底関数のベクトル,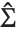 はパラメータに対する推定分散行列である.単一の予測区間は,予測子の固定値において
はパラメータに対する推定分散行列である.単一の予測区間は,予測子の固定値において 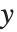 を予測するための信頼区間を与えるもので,
を予測するための信頼区間を与えるもので,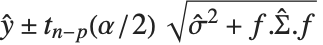 で与えられる.ここで
で与えられる.ここで 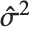 は推定誤差分散である.
は推定誤差分散である.
適合度はモデルがどの程度フィットしているかを評価するため,あるいはモデルを比較するために使用される.決定係数"RSquared"は,総平方和に対するモデルの平方和の比である."AdjustedRSquared"はモデルのパラメータの数に対して罰則付きで, により与えられる.
により与えられる.
"AIC"と"BIC"は尤度に基づき適合度を測定する.これはどちらもモデルの対数尤度の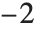 倍に
倍に 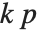 (
(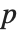 は予測される分散を含む,予測されるパラメータの数)を足したものに等しい."AIC" では
は予測される分散を含む,予測されるパラメータの数)を足したものに等しい."AIC" では  が
が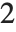 のとき,"BIC"では
のとき,"BIC"では 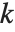 は
は である.
である.
一般化された線形モデル
線形モデルはそれぞれの応答値  が平均値
が平均値 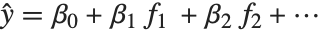 の正規分布からの観察となっているモデルとみることができる.一般化された線形モデルは,形式
の正規分布からの観察となっているモデルとみることができる.一般化された線形モデルは,形式 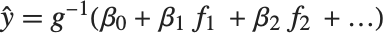 のモデルに拡張される.ここでそれぞれの
のモデルに拡張される.ここでそれぞれの 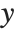 は,平均が
は,平均が 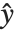 で
で  が指数型分布族のサポート上の可逆関数である,既知の指数型分布族からの観察であると想定される.この種類のモデルはGeneralizedLinearModelFitで得ることができる.
が指数型分布族のサポート上の可逆関数である,既知の指数型分布族からの観察であると想定される.この種類のモデルはGeneralizedLinearModelFitで得ることができる.
| GeneralizedLinearModelFit[{y1,y2,…},{f1,f2,…},x] | 基底関数 fi,単独の予測変数 x の一般化された線形モデルを得る |
| GeneralizedLinearModelFit[{{x11,x12,…,y1},{x21,x22,…,y2}},{f1,f2,…},{x1,x2,…}] | 複数の予測変数 xi の一般化された線形モデルを得る |
| GeneralizedLinearModelFit[{m,v}] | 計画行列 m と応答ベクトル v に基づく一般化された線形モデルを得る |
可逆関数 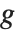 は連結関数と呼ばれ,線形結合
は連結関数と呼ばれ,線形結合 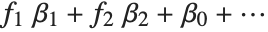 は線形予測子と呼ばれる.一般的な特殊ケースとして,恒等リンク関数とガウスまたは正規の指数型分布族を持つ線形回帰モデル,確率に対するロジットおよびプロビットモデル,カウントデータに対するポアソンモデル,ガンマおよび逆ガウスモデルがある.
は線形予測子と呼ばれる.一般的な特殊ケースとして,恒等リンク関数とガウスまたは正規の指数型分布族を持つ線形回帰モデル,確率に対するロジットおよびプロビットモデル,カウントデータに対するポアソンモデル,ガンマおよび逆ガウスモデルがある.
誤差分散は予測  の関数であり,分散パラメータとして言及される定数
の関数であり,分散パラメータとして言及される定数  までの分布により定義される.フィットされた値に対する誤差分散
までの分布により定義される.フィットされた値に対する誤差分散 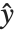 は
は  と書くことができる.ここで
と書くことができる.ここで 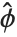 は観察された応答値および予測された応答力得られた分散パラメータであり,
は観察された応答値および予測された応答力得られた分散パラメータであり, は指数型分布族に関連付けられた分散関数である.
は指数型分布族に関連付けられた分散関数である.
ロジットおよびプロビットモデルは確率でよく使われる二項モデルである.ロジットモデルの連結関数は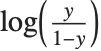 であり,プロビットモデルの連結関数は標準の正規分布
であり,プロビットモデルの連結関数は標準の正規分布 に対してはCDFの逆関数である.このタイプのモデルは,ExponentialFamily->"Binomial"で適切なLinkFunctionを持つGeneralizedLinearModelFit,またはLogitModelFit,ProbitModelFitでフィットすることができる.
に対してはCDFの逆関数である.このタイプのモデルは,ExponentialFamily->"Binomial"で適切なLinkFunctionを持つGeneralizedLinearModelFit,またはLogitModelFit,ProbitModelFitでフィットすることができる.
| LogitModelFit[data,funs,vars] | 基底関数 funs,予測子変数 vars のロジットモデルを得る |
| LogitModelFit[{m,v}] | 計画行列 m,応答ベクトル v のロジットモデルを得る |
| ProbitModelFit[data,funs,vars] | data に対するプロビットモデルのフィットを得る |
| ProbitModelFit[{m,v}] | 計画行列 m,応答ベクトル v へのプロビットモデルのフィットを得る |
パラメータ推定は,想定される分布の分散関数から得られた重みで繰返し最小二乗に重みを付けることにより得られる.GeneralizedLinearModelFitのオプションには,PrecisionGoal等の反復フィットに対するオプション,LinkFunction等のモデル指定に対するオプション,ConfidenceLevel等の更なる解析のためのオプションが含まれる.
オプション名
|
デフォルト値
| |
| AccuracyGoal | Automatic | 目標確度 |
| ConfidenceLevel | 95/100 | パラメータと予測の信頼水準 |
| CovarianceEstimatorFunction | "ExpectedInformation" | パラメータ共分散行列のための推定法 |
| DispersionEstimatorFunction | Automatic | 誤差分散を推定する値または関数 |
| ExponentialFamily | Automatic | y の指数型分布 |
| IncludeConstantBasis | True | 定数基底関数を入れるかどうか |
| LinearOffsetFunction | None | 線形予測量における既知のオフセット |
| LinkFunction | Automatic | モデルの連結関数 |
| MaxIterations | Automatic | 使用する最大反復回数 |
| NominalVariables | None | 名義的,カテゴリ的とみなされる関数 |
| PrecisionGoal | Automatic | 目標とする精度 |
| Weights | Automatic | データ要素の重み |
| WorkingPrecision | Automatic | 内部計算で使われる精度 |
GeneralizedLinearModelFitで使用可能なオプション
LogitModelFitおよびProbitModelFitのオプションはGeneralizedLinearModelFitのオプションと同じであるが,異なる点はExponentialFamilyとLinkFunctionはロジットあるいはプロビットモデルにより定義されるため,これらはLogitModelFitおよびProbitModelFitのオプションではないという点だけである.
ExponentialFamilyには"Binomial","Gamma","Gaussian","InverseGaussian","Poisson","QuasiLikelihood"を取ることができる.二項モデルは0から1までの応答に有効である.ポワソンモデルは非負の整数の応答に有効である.ガウス,正規モデルは実数応答に,ガンマおよび逆ガンマモデルは正の応答に有効である.擬似尤度モデルは, 番目のデータ点に対する擬似尤度関数の対数が
番目のデータ点に対する擬似尤度関数の対数が  で与えられるような分散関数
で与えられるような分散関数  で分布構造を定義する."QuasiLikelihood"モデルの分散関数は,オプションでExponentialFamily->{"QuasiLikelihood", "VarianceFunction"->fun}として設定することができる.ここで fun はフィットされた値に適用される純関数である.
で分布構造を定義する."QuasiLikelihood"モデルの分散関数は,オプションでExponentialFamily->{"QuasiLikelihood", "VarianceFunction"->fun}として設定することができる.ここで fun はフィットされた値に適用される純関数である.
ExponentialFamily,IncludeConstantBasis,LinearOffsetFunction,LinkFunction,NominalVariables,Weightsはすべてモデル構造および最適化基準のある部分を定義し,GeneralizedLinearModelFitの内部だけで設定することができる.他のオプションはすべてGeneralizedLinearModelFit内で設定することもできるし,結果と診断を得るときにFittedModelに渡すこともできる.FittedModelオブジェクトの評価において設定されるオプションはフィットの段階でGeneralizedLinearModelFitに与えられている設定より優位になる.
| "BasisFunctions" | 基底関数のリスト |
| "BestFit" | フィットされた関数 |
| "BestFitParameters" | パラメータ推定 |
| "Data" | 入力データあるいは計画行列と応答ベクトル |
| "DesignMatrix" | モデルに対する計画行列 |
| "Function" | 最適フィットの純関数 |
| "LinearPredictor" | フィットされた線形結合 |
| "Response" | 入力データにおける応答値 |
"BestFitParameters"は基底関数に対するパラメータ推定を与える."BestFit"はフィットされた関数  を,"LinearPredictor"は線形結合
を,"LinearPredictor"は線形結合  を与える."BasisFunctions"は,定数項がモデルに存在する場合に
を与える."BasisFunctions"は,定数項がモデルに存在する場合に 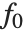 を定数1とした関数
を定数1とした関数 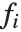 のリストを与える."DesignMatrix"は基底関数についての計画行列あるいはモデル行列である.
のリストを与える."DesignMatrix"は基底関数についての計画行列あるいはモデル行列である.
| "Deviances" | 尤離度 |
| "DevianceTable" | 尤離度表 |
| "DevianceTableDegreesOfFreedom" | 表からの自由度の差 |
| "DevianceTableDeviances" | 表からの尤離度の差 |
| "DevianceTableEntries" | 表からのフォーマットされていない値の配列 |
| "DevianceTableResidualDegreesOfFreedom" | 表からの自由度残差 |
| "DevianceTableResidualDeviances" | 表からの残差の尤離度 |
| "EstimatedDispersion" | 予測分散パラメータ |
| "NullDeviance" | ヌルモデルの尤離度 |
| "NullDegreesOfFreedom" | ヌルモデルの自由度 |
| "ResidualDeviance" | フィットしたモデルでの分散と完全モデルでの分散との差分 |
| "ResidualDegreesOfFreedom" | モデル自由度とヌル自由度の差 |
尤離度と尤離度表は線形モデルの分散分析により与えられるモデルの分解を一般化する.単独のデータ点に対する尤離度は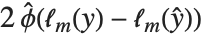 であり,ここで
であり,ここで 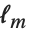 はフィットされたモデルの対数尤度関数である."Deviances"はすべてのデータ点に対する尤離値のリストを与える.すべての尤離度の総和はモデルの尤離度を与える.モデルの尤離度は,線形モデルで平方和がANOVA表にあるときは分解することができる.この完全モデルでは,予測された値がデータと同じである.
はフィットされたモデルの対数尤度関数である."Deviances"はすべてのデータ点に対する尤離値のリストを与える.すべての尤離度の総和はモデルの尤離度を与える.モデルの尤離度は,線形モデルで平方和がANOVA表にあるときは分解することができる.この完全モデルでは,予測された値がデータと同じである.
平方和の場合と同じように,尤離度は加法的である.表のDevianceの列で,与えられた基底関数が加えられるとモデルの尤離度が増すことが分かる.Residual Devianceの列はモデルの尤離度と表の中のすべての項を含む部分も出るの尤離度との差分を与える.大きい標本の場合,尤離度の増加は自由度が表の基底関数の自由度に等しい  分布にほぼ従っている.
分布にほぼ従っている.
| "AnscombeResiduals" |
アンスコム(Anscombe)残差
|
| "DevianceResiduals" | 尤離度残差 |
| "FitResiduals" | 実際の応答と予想された応答の差 |
| "LikelihoodResiduals" | 尤度残差 |
| "PearsonResiduals" |
ピアソン(Pearson)残差
|
| "StandardizedDevianceResiduals" | 標準化された尤離度残差 |
| "StandardizedPearsonResiduals" | 標準化されたピアソン残差 |
| "WorkingResiduals" | 作業残差 |
"FitResiduals"は残差,つまり観察された応答と予測された応答との差分のリストである.分布の仮定があるとき,残差の大きさは予測された応答値の関数として変化するものと想定される.一般化された線形モデルの分析では,スケールされた残差のさまざまなタイプが使われる.
| "CorrelationMatrix" | 漸近的なパラメータ相関行列 |
| "CovarianceMatrix" | 漸近的なパラメータ共分散行列 |
| "ParameterConfidenceIntervals" | パラメータの信頼区間 |
| "ParameterConfidenceIntervalTable" | フィットされたパラメータの信頼区間情報の表 |
| "ParameterConfidenceIntervalTableEntries" | 表からのフォーマットされていない値の配列 |
| "ParameterConfidenceRegion" | 楕円体パラメータ信頼領域 |
| "ParameterTableEntries" | 表からのフォーマットされていない値の配列 |
| "ParameterErrors" | 予測パラメータの標準誤差 |
| "ParameterPValues" | パラメータ |
| "ParameterTable" | フィットされたパラメータ情報の表 |
| "ParameterZStatistics" | パラメータ推定の |
"CovarianceMatrix"はフィットされたパラメータ間の共分散を与え,線形モデルの定義に非常に類似している.CovarianceEstimatorFunction->"ExpectedInformation"の設定では,反復フィットにより得られる想定された情報行列が使われる.この行列は  であり,
であり, は計画行列,
は計画行列, はフィットの最終段階からの重みの対角行列である.重みにはWeightsオプションで指定された重みおよび分布の分散関数に関連付けられた重みが含まれる.CovarianceEstimatorFunction->"ObservedInformation"と設定すると,この行列は
はフィットの最終段階からの重みの対角行列である.重みにはWeightsオプションで指定された重みおよび分布の分散関数に関連付けられた重みが含まれる.CovarianceEstimatorFunction->"ObservedInformation"と設定すると,この行列は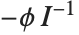 により与えられる.ここで
により与えられる.ここで 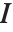 はそのモデルのパラメータについて対数尤度関数のヘッシアンである,観察されたフィッシャー(Fisher)情報行列である.
はそのモデルのパラメータについて対数尤度関数のヘッシアンである,観察されたフィッシャー(Fisher)情報行列である.
"CorrelationMatrix"はパラメータ推定に対して関連付けられた共分散行列である."ParameterErrors"は共分散行列の対角要素の平方根と等価である. "ParameterTable"および"ParameterConfidenceIntervalTable"には個々のパラメータ推定,パラメータ有意度の検定,信頼区間に関する情報が含まれる.一般化された線形モデルの検定統計量は漸近的に正規分布に従う.
"CookDistances"および"HatDiagonal"はその影響力の測定を線形回帰から一般化された線形モデルへと拡張する.対角要素が抽出されたハット行列は,反復フィットの最終的な重みを使って定義される.
| "AdjustedLikelihoodRatioIndex" | Ben‐AkivaとLermanの修正尤度比指数 |
| "AIC" | 赤池情報量基準 |
| "BIC" |
ベイズ(Bayes)情報量基準
|
| "CoxSnellPseudoRSquared" | CoxとSnellの擬似 |
| "CraggUhlerPseudoRSquared" | CraggとUhlerの擬似 |
| "EfronPseudoRSquared" | Efronの擬似 |
| "LikelihoodRatioIndex" | McFaddenの尤度比指数 |
| "LikelihoodRatioStatistic" | 尤度比 |
| "LogLikelihood" | フィットされたモデルのための対数尤度 |
| "PearsonChiSquare" | ピアソンの |
"LogLikelihood"はフィットされたモデルに対する対数尤度である."AIC"および"BIC"は罰則付き対数尤度 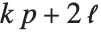 である.ここで
である.ここで 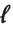 はフィットされたモデルに対する対数尤度,
はフィットされたモデルに対する対数尤度, は分散パラメータを含む推定されるパラメータ数,
は分散パラメータを含む推定されるパラメータ数,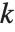 は
は 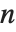 個のデータ点のモデルにおいて"AIC"では2,"BIC"では
個のデータ点のモデルにおいて"AIC"では2,"BIC"では である."LikelihoodRatioStatistic"は
である."LikelihoodRatioStatistic"は により与えられ,
により与えられ, はヌルモデルの対数尤度を表す.
はヌルモデルの対数尤度を表す.
多数の適合度の尺度では,線形回帰の  を説明されたバリエーションの尺度あるいは尤度ベースの尺度として一般化する."CoxSnellPseudoRSquared"は
を説明されたバリエーションの尺度あるいは尤度ベースの尺度として一般化する."CoxSnellPseudoRSquared"は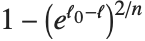 により与えられる."CraggUhlerPseudoRSquared"はCoxとSnellの尺度
により与えられる."CraggUhlerPseudoRSquared"はCoxとSnellの尺度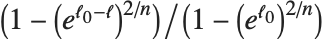 をスケールしたものである."LikelihoodRatioIndex"には対数尤度
をスケールしたものである."LikelihoodRatioIndex"には対数尤度 の比が関わっており,"AdjustedLikelihoodRatioIndex"はパラメータの数
の比が関わっており,"AdjustedLikelihoodRatioIndex"はパラメータの数 で罰則が付いて適合する."EfronPseudoRSquared"は
で罰則が付いて適合する."EfronPseudoRSquared"は 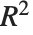 の平方和の解釈を使い,
の平方和の解釈を使い, (ここで
(ここで  は
は  番目の残差,
番目の残差, は応答
は応答 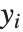 の平均である)として与えられる.
の平均である)として与えられる.
非線形モデル
非線形の最小二乗モデルは線形モデルの拡張であり,ここではモデルは基底関数の線形結合である必要はない.誤差は独立であると想定され,正規分布に従う.このタイプのモデルはNonlinearModelFit関数を使ってフィットすることができる.
| NonlinearModelFit[{y1,y2,…},form,{β1,…},x] | パラメータ βi,単独のパラメータ予測子変数 x の関数 form の非線形モデルを得る |
| NonlinearModelFit[{{x11,…,y1},{x21,…,y2}},form,{β1,…},{x1,…}] | 複数の予測子変数 xi の関数として非線形モデルを得る |
| NonlinearModelFit[data,{form,cons},{β1,…},{x1,…}] | 制約条件 cons に従う非線形モデルを得る |
非線形モデルの形式は  であり,ここで
であり,ここで  はフィットされた,あるいは予測された値,
はフィットされた,あるいは予測された値,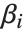 はフィットされるパラメータ,
はフィットされるパラメータ,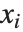 は予測子変数である.他の非線形最適化問題すべてでそうであるように,パラメータの初期値によい値を選ぶことが大切である.初期値はFindFitと同じパラメータ指定を使って与えることができる.
は予測子変数である.他の非線形最適化問題すべてでそうであるように,パラメータの初期値によい値を選ぶことが大切である.初期値はFindFitと同じパラメータ指定を使って与えることができる.
オプション名
|
デフォルト値
| |
| AccuracyGoal | Automatic | 目標確度の桁数 |
| ConfidenceLevel | 95/100 | パラメータと予測の信頼性のレベル |
| EvaluationMonitor | None | expr が評価されるたびに評価する式 |
| MaxIterations | Automatic | 使用する最大反復回数 |
| Method | Automatic | 使用するメソッド |
| PrecisionGoal | Automatic | 目標精度 |
| StepMonitor | None | ステップが取られるたびに評価される式 |
| VarianceEstimatorFunction | Automatic | 誤差分散を推定するための値または関数 |
| Weights | Automatic | データ要素の重み |
| WorkingPrecision | Automatic | 内部計算で使われる精度 |
NonlinearModelFitで使用可能なオプション
Weightsオプションは重み付きの非線形回帰に対する重みの値を指定する.最適なフィットは重み付き誤差平方和に対するものである.
他のオプションはすべて初期フィットの後の結果の計算に関連し得る.これらのオプションは,フィットで使用するためにNonlinearModelFit内で設定することも,FittedModelオブジェクトから得られた結果に対するデフォルト設定を指定するため設定することもできる.これらのオプションはすでに構築されたFittedModelオブジェクト内で設定して,はじめにNonlinearModelFitに与えられたオプション値をオーバーライドすることもできる.
| "BestFit" | フィットされた関数 |
| "BestFitParameters" | パラメータの推定 |
| "Data" | 入力データ |
| "Function" | 最もよくフィットした純関数 |
| "Response" | 入力データの応答値 |
非線形モデルのデータおよびフィットされた関数の基本的な特性は線形および一般化された線形モデルでの同じ特性と同様に動作する.例外は"BestFitParameters"がFindFitの結果に対して行われるような規則を返すという点である.
| "FitResiduals" | 実際の応答と予想された応答の差 |
| "StandardizedResiduals" | 各余剰について標準誤差で割った余剰のフィット |
| "StudentizedResiduals" | 単一の削除誤差推定で割った剰余のフィット |
線形回帰の場合と同様に,"FitResiduals"は観察された値とフィットされた値との間の差分 を与える."StandardizedResiduals"と"StudentizedResiduals"はこれらの差分をスケールした形式である.
を与える."StandardizedResiduals"と"StudentizedResiduals"はこれらの差分をスケールした形式である.
標準化された 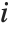 番目の残差は
番目の残差は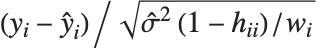 である.ここで
である.ここで 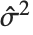 は推定誤差分散,
は推定誤差分散,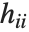 はハット行列の
はハット行列の 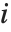 番目の対角要素,
番目の対角要素,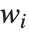 は
は 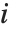 番目のデータ点に対する重み,スチューデント化された
番目のデータ点に対する重み,スチューデント化された  番目の残差は
番目の残差は 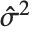 を
を  番目の単独削除変数
番目の単独削除変数  で置き換えて得られる.非線形モデルの場合は,計画行列に対して一次近似が使われるが,これはハット行列を計算するのに必要なのである.
で置き換えて得られる.非線形モデルの場合は,計画行列に対して一次近似が使われるが,これはハット行列を計算するのに必要なのである.
| "ANOVATable" | 分散分析表 |
| "ANOVATableDegreesOfFreedom" | ANOVA表からの自由度 |
| "ANOVATableEntries" | 表からのフォーマットされていない配列の値 |
| "ANOVATableMeanSquares" | 表からの平方平均誤差 |
| "ANOVATableSumsOfSquares" | 表からの平方和 |
| "EstimatedVariance" | 誤差分散の推定 |
| "CorrelationMatrix" | 漸近的なパラメータ相関行列 |
| "CovarianceMatrix" | 漸近的なパラメータ共分散行列 |
| "ParameterBias" | パラメータ推定の推定の偏り |
| "ParameterConfidenceIntervals" | パラメータの信頼区間 |
| "ParameterConfidenceIntervalTable" | フィットされたパラメータの信頼区間情報の表 |
| "ParameterConfidenceIntervalTableEntries" | 表からのフォーマットされていない値の配列 |
| "ParameterConfidenceRegion" | 楕円体パラメータ信頼領域 |
| "ParameterErrors" | 予測パラメータの標準誤差 |
| "ParameterPValues" | パラメータ |
| "ParameterTable" | フィットされたパラメータ情報の表 |
| "ParameterTableEntries" | 表からのフォーマットされていない値の配列 |
| "ParameterTStatistics" | パラメータ推定の |
"CovarianceMatrix"はフィットされたパラメータ間の近似共分散を与える.この行列は  であり,ここで
であり,ここで 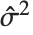 は分散推定,
は分散推定,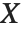 はモデルに対する線形近似の計画行列,
はモデルに対する線形近似の計画行列, は重みの対角行列である."CorrelationMatrix"はパラメータ推定値に対して関連付けられた相関行列である."ParameterErrors"は共分散行列の対角要素の平方根と等価である.
は重みの対角行列である."CorrelationMatrix"はパラメータ推定値に対して関連付けられた相関行列である."ParameterErrors"は共分散行列の対角要素の平方根と等価である.
"ParameterTable"および"ParameterConfidenceIntervalTable"には,誤差推定を使って得られた個々のパラメータ推定値,パラメータ有意性の検定,信頼区間についての情報が含まれる.
| "CurvatureConfidenceRegion" | 曲率診断の信頼区間 |
| "FitCurvatureTable" | 曲率診断表 |
| "FitCurvatureTableEntries" | 表からのフォーマットされていない値の配列 |
| "MaxIntrinsicCurvature" | 最大内部曲率尺度 |
| "MaxParameterEffectsCurvature" | パラメータ効果曲率の尺度 |
多くの診断で使われる一次近似はモデルがパラメータで線形であることに等しい.パラメータ推定付近のパラメータ空間が十分平坦な場合,線形近似および一次近似に依存するあらゆる結果は有効であるとみなされる.近似による線形性が有効であるかどうかを評価するために曲率診断が使われる."FitCurvatureTable"は曲率診断の表である.
"MaxIntrinsicCurvature"および"MaxParameterEffectsCurvature"は最もよくフィットしたパラメータ値におけるパラメータ空間の法曲率および正接曲率をスケールした尺度である."CurvatureConfidenceRegion"は最もよくフィットしたパラメータ値におけるパラメータ空間の曲率半径をスケールした尺度である.法曲率と正接曲率が"CurvatureConfidenceRegion"の値に対して小さい場合,線形近似が妥当であるとみなされる.経験則にはその値を直接比較することを勧めるものもあれば,"CurvatureConfidenceRegion"の半分と比較することを勧めるものもある.
ハット行列は  となるような行列
となるような行列 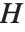 である.ここで
である.ここで 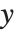 は観察された応答,
は観察された応答, は予測された応答ベクトルである."HatDiagonal"はハット行列の診断的要素を与える.他の特性と同様に,
は予測された応答ベクトルである."HatDiagonal"はハット行列の診断的要素を与える.他の特性と同様に, はモデルへの線形近似に計画行列を使う.
はモデルへの線形近似に計画行列を使う.
| "MeanPredictionBands" | 平均予測の信頼帯 |
| "MeanPredictionConfidenceIntervals" | 平均予測の信頼区間 |
| "MeanPredictionConfidenceIntervalTable" | 平均予測の信頼区間表 |
| "MeanPredictionConfidenceIntervalTableEntries" | 表からのフォーマットされていない値の配列 |
| "MeanPredictionErrors" | 平均予測の標準誤差 |
| "PredictedResponse" | データのフィットされた値 |
| "SinglePredictionBands" | 1回の観察に基づいた信頼帯 |
| "SinglePredictionConfidenceIntervals" | 1回の観察の予想される応答の信頼区間 |
| "SinglePredictionConfidenceIntervalTable" | 1回の観察の予想される応答の信頼区間の表 |
| "SinglePredictionConfidenceIntervalTableEntries" | 表からのフォーマットされていない値の配列 |
| "SinglePredictionErrors" | 1回の観察の予測応答の標準誤差 |
信頼区間に対する表の結果は"MeanPredictionConfidenceIntervalTable"および"SinglePredictionConfidenceIntervalTable"で与えられる.これらの結果は線形モデルの場合にLinearModelFitで得られる結果と同じである.ここでも計画行列に一次近似が使われる.
"AdjustedRSquared","AIC","BIC","RSquared"は,線形モデルに対して定義されているように,すべて尺度を直接拡張したものである.決定係数"RSquared"は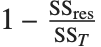 であり,
であり, は平方和の残差,
は平方和の残差, は未補正の全平方和である.非線形モデルでは,決定係数は線形モデルでそうであるような,説明された分散の割合と同じ解釈は持たない.それは,モデルに対する平方和と残差に対する平方和が必ずしも全平方和にはならないからである."AdjustedRSquared"はモデルのパラメータ数について罰則が付き,
は未補正の全平方和である.非線形モデルでは,決定係数は線形モデルでそうであるような,説明された分散の割合と同じ解釈は持たない.それは,モデルに対する平方和と残差に対する平方和が必ずしも全平方和にはならないからである."AdjustedRSquared"はモデルのパラメータ数について罰則が付き, により与えられる.
により与えられる.
多くの数値計算では,近似関数を導入すると便利である.近似関数とは普通に使う実数の近似を一般化したものと考えればよい.すなわち,実数の近似数がある数値的な量を特定の桁精度で表すならば,近似関数は単一,もしくは複数のパラメータに依存した量を特定の精度で表すもの,ととらえる.Wolfram言語では,NDSolveを使い求めた微分方程式の解を表すために近似関数が使われている.詳しくは,「微分方程式の数値解法」を参照のこと.
Wolfram言語における近似関数はInterpolatingFunctionオブジェクトで表される.この補間オブジェクトは「純関数」で説明した純関数と同じように機能する.InterpolatingFunctionの基本的な機能は,特定の引数を与えたときにその引数に対応する近似関数の値を与えることである.
InterpolatingFunctionは内挿手法に基づいた近似関数を与える.通常,一連の点における関数値を持つが,さらに微分値を持つときもある.また,補間法の前提として,関数がデータ点の間で滑らかに変化するものとされる.このInterpolatingFunctionに任意点における関数の値を要求すると,データから内挿処理がなされ,必要な値が近似される.
| Interpolation[{f1,f2,…}] | 連続した整数点におけるデータ値 fi をもとに補間法を使い近似関数を構築する |
| Interpolation[{{x1,f1},{x2,f2},…}] | |
変数の点 xi におけるデータ値 fi をもとに補間法を使い近似関数を構築する | |
InterpolatingFunctionオブジェクトには,Wolfram言語の処理で必要になる,近似関数に関する情報がすべて含まれる.標準的なWolfram言語の出力表記を使っている場合,InterpolatingFunctionオブジェクトの定義域を与える部分だけが表示される.InterpolatingFunctionオブジェクトで実際に使われたパラメータは略式表示される.
標準出力表記では,InterpolatingFunctionオブジェクトの定義域と出力型だけが具体的に表示される:
| Interpolation[{{{x1},f1,df1,ddf1,…},…}] | |
近似関数の構築において点 xi における導関数も補間データとして使う | |
Interpolationは,データ点を多項式曲線でフィットさせるために使う.曲線の次数を指定するときにはオプションInterpolationOrderを使う.このオプションはデフォルトで,InterpolationOrder->3の設定になっているので,特に指定しなければ三次曲線でフィット処理が行われる.
デフォルトのままだと,InterpolationOrder->3が有効なので,三次曲線でフィット処理が行われる.三次でも関数は滑らかである:
通常,InterpolationOrderの設定値を高くすればするほど,より滑らかな近似関数が得られる.ただし,高く設定しすぎると,曲線にまばらな振動部が現れてしまう.
| ListInterpolation[{{f11,f12,…},{f21,…},…}] | |
格子状の2D座標平面における各整数格子点における値を補間する関数を構築する | |
| ListInterpolation[list,{{xmin,xmax},{ymin,ymax}}] | |
等間隔で区画化した格子状の2D座標平面を前提とする | |
| ListInterpolation[list,{{x1,x2,…},{y1,y2,…}}] | |
任意間隔で区画化した格子状の2D座標平面を前提とする | |
生成されたInterpolatingFunctionオブジェクトには引数が3ついる:
近似関数をもとにした処理を行っていると,複雑に組み合さったInterpolatingFunctionオブジェクトが得られてしまうことがよくある.そのようなときは,特定の定義域についてFunctionInterpolationを適用させることで単一のInterpolatingFunctionオブジェクトに統合できる.
定義域を0から1とするInterpolatingFunctionオブジェクトを新たに生成する:
ネストしたInterpolatingFunctionオブジェクトを生成する:
純粋な二次元InterpolatingFunctionオブジェクトを生成する:
| FunctionInterpolation[expr,{x,xmin,xmax}] | |
式 expr を x が xmin から xmax まで評価することで近似関数を構築する | |
| FunctionInterpolation[expr,{x,xmin,xmax},{y,ymin,ymax},…] | |
多次元で有効な近似関数を構築する | |
データ解析でよく使われる標準的な解析手法に,値のリストの離散フーリエ(Fourier)変換(またはスペクトル解析)がある.フーリエ変換の基本は,特定の周波数点や帯域においてデータがどのような強度の信号成分を持つかを調べることにある.
| Fourier[{u1,u2,…,un}] | 離散フーリエ変換 |
| InverseFourier[{v1,v2,…,vn}] | 逆離散フーリエ変換 |
Fourierはデータの総数が2のベキ乗であるか否かにかかわらず機能する:
科学技術分野では離散フーリエ変換の定義は分野によってさまざまな規約がある.オプションFourierParametersを使用して必要な規約を選択することができる.
さまざまな規約でのFourierParametersの典型的な設定
| Fourier[{{u11,u12,…},{u21,u22,…},…}] | |
二次元離散フーリエ変換 | |
実数データに対する通常の離散フーリエ変換に関する問題のひとつに,結果が複素数値になるというものがある.実数のフーリエ変換で実数の結果を出す種類のものもある.Wolfram言語には離散余弦変換と離散正弦変換を計算するためのコマンドがある.
| FourierDCT[list] | 実数のリストのフーリエ離散余弦変換 |
| FourierDST[list] | 実数のリストのフーリエ離散正弦変換 |
| FourierDCT[list,m] | タイプ m のフーリエ離散余弦変換 |
| FourierDST[list,m] | タイプ m のフーリエ離散正弦変換 |
Wolfram言語にはInverseFourierDCT関数とInverseFourierDST関数は必要ない.それはFourierDCTとFourierDSTが適切なタイプで使用されると,それ自身の逆関数となるからである.タイプ1,2,3,4の逆変換はそれぞれタイプ1,3,2,4となる.
| ListConvolve[kernel,list] | kernel と list のたたみ込みの形成 |
| ListCorrelate[kernel,list] | kernel と list の相関の形成 |
この場合,核を反転するとListConvolveと全く同じ結果が得られる:
核と結合させるサブリストを構成する際,データリストの最後をどう扱うかが常に問題になる.デフォルトではListConvolveおよびListCorrelateはデータリストの最後から「はみ出す」サブリストは作成しない.これは得られる結果が通常はもとのデータリストより短いことを意味している.
実際上,もとのデータリストと同じ長さの出力を得たい場合がしばしばある.このためにはデータリストの片側または両側がはみ出すようなサブリストが必要となる.こういったサブリストの形成に必要な追加要素は,ある種の「パディング」で充填される必要がある.デフォルトではWolfram言語は,もとのリストの複製を作り,パディングを与え,リストを循環的に扱うようになっている.
| ListCorrelate[kernel,list] | どちら側にもはみ出しを許さない(結果は list より短い) |
| ListCorrelate[kernel,list,1] | 右側にはみ出しを許す(結果は list と同じ長さ) |
| ListCorrelate[kernel,list,-1] | 左側にはみ出しを許す(結果は list と同じ長さ) |
| ListCorrelate[kernel,list,{-1,1}] | 両側にはみ出しを許す(結果は list よりも長い) |
| ListCorrelate[kernel,list,{kL,kR}] | 左側および右側に特別なはみ出しを許す |
一般的な場合,ListCorrelate[kernel,list,{kL,kR}]は,結果の最初の要素では list の最初の要素が kernel の位置 kL にある要素と掛けられ,結果の最後の要素では list の最後の要素が kernel の位置 kR にある要素と掛けられるようになっている.したがって,はみ出しがどちら側にも許されないとされるデフォルトの場合はListCorrelate[kernel,list,{1,-1}]に相当する.
| ListCorrelate[kernel,list,klist,p] | 要素 p で充填する |
| ListCorrelate[kernel,list,klist,{p1,p2,…}] | |
pi の循環で充填 | |
| ListCorrelate[kernel,list,klist,list] | もとのデータの循環で充填 |
| CellularAutomaton[rnum,init,t] | 進化ルール rnum で init から t ステップ進化させる |
| {a1,a2,…} | 値 ai の明示的リスト |
| {{a1,a2,…},b} | b 背景に重ねた値 ai |
| {{a1,a2,…},blist} | blist の反復による背景に重ねた値 ai |
| {{{{a11,a12,…},{d1}},…},blist} | オフセット di による値 aij |
初期値の明示的なリストを与えると,CellularAutomatonはリスト中の要素を反復させることでシステムのすべてのセルに対応すると考える.
小さな「種」区域を安定した「背景」に重ねるように初期条件を設定すると便利なことがよくある.デフォルトは,CellularAutomatonは指定された進化ステップ数で作られるパターンの大きさをカバーするに足る背景を自動的に埋める.
| n | |
| {n,k} | k 色の一般最近傍ルール |
| {n,k,r} | k 色で範囲 r の一般ルール |
| {n,{k,1}} | k の最近傍totalisticルール |
| {n,{k,1},r} | k 色で範囲 r のtotalisticルール |
| {n,{k,{wt1,wt2,…}},r} | 近傍 i に重み wti が割り当てられたルール |
| {n,kspec,{{off1},{off2},…,{offs}}} | 指定のオフセットの近傍ルール |
| {lhs1->rhs1,lhs2->rhs2,…} | 近傍ルールの明示的な置換 |
| {fun,{},rspec} | 関数 fun を各近傍リストに適用して得られるルール |
最も単純な場合は,セルオートマトンは各セルに k 個の可能な値あるいは「色」を許容し,各辺で最高 r までの近傍を含むルールを持つ.「ルール番号」n の各桁の数字は各近傍の可能な設定において新たなセルが何色になるかを指定する.
一般的なセルオートマトンのルールでは,ルール番号の各桁の数字が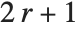 個のセルの可能な近傍が何色になるかを指定する.どの数字がどの近傍に当たるのかが知りたければ近傍中のセルを数字の桁とみなせばよい.
個のセルの可能な近傍が何色になるかを指定する.どの数字がどの近傍に当たるのかが知りたければ近傍中のセルを数字の桁とみなせばよい. のセルオートマトンでは数字は neig.{k^2,k,1}によって近傍中の要素 neig のリストから得られる.
のセルオートマトンでは数字は neig.{k^2,k,1}によって近傍中の要素 neig のリストから得られる.
「totalistic 」なセルオートマトンを考慮するとよいこともある.「totalistic 」なセルオートマトンではセルの新たな値が近傍の値の合計のみに依存する.「totalistic 」なセルオートマトンはルール番号あるいは各桁の数字が例えば neig.{1,1,1}から得られるように,与えられた総和の値で近傍を参照する「コード」で指定することができる.
一般に,CellularAutomatonを使っていかなる重みのシーケンスを使ったルールでも指定することができる.これとはまた別の便利な点に{k,1,k}がある.これはouter totalisticルールを与える.
任意の  セルオートマトンルールはブール関数に対応すると考えることができる.最も単純な例として,AndまたはNorのような基本的なブール関数は2つの引数を取る.これはセルオートマトンのルールを使ってオフセット{{0},{1}}であると指定することができる.より高次元のセルオートマトンを扱う上での互換性のために,たとえ一次元のセルオートマトンであってもオフセットは常にリストで与える点に注意のこと.
セルオートマトンルールはブール関数に対応すると考えることができる.最も単純な例として,AndまたはNorのような基本的なブール関数は2つの引数を取る.これはセルオートマトンのルールを使ってオフセット{{0},{1}}であると指定することができる.より高次元のセルオートマトンを扱う上での互換性のために,たとえ一次元のセルオートマトンであってもオフセットは常にリストで与える点に注意のこと.
| CellularAutomaton[rnum,init,t] | すべてのステップを保存しながら t ステップ進化する |
| CellularAutomaton[rnum,init,{{t}}] | 最後のステップだけを保存して t ステップ進化する |
| CellularAutomaton[rnum,init,{spect}] | spect で指定されたステップだけを保存する |
| CellularAutomaton[rnum,init] | 規則を1ステップ分進化させ,最後のステップだけを返す |
ステップ指定 spect はTakeを使ってリストから要素を取り出すのに似ている.違いは,セルオートマトンの初期条件がステップ0とみなされる点である.{…}の形式のステップ指定はどれも追加リストに埋め込まれていなければならない.
| CellularAutomaton[rnum,init,t] | すべてのステップとすべての関連するセルを保存する |
| CellularAutomaton[rnum,init,{spect,specx}] | 指定されたステップとセルだけを保存する |
セルオートマトンの進化の過程でどのステップを保存するかを指定できるように,どのセルを保存するかも指定できる.{{a1,a2,…},blist} のような初期条件を与えると,rd はどのセルを保存するかを指定するためにオフセットが0であると解釈される.
| All | 指定された初期条件に影響されるすべてのセル |
| Automatic | 領域内の背景とは異なるすべてのセル(デフォルト) |
| 0 | aspec のはじめと並んでいるセル |
| x | 右側にオフセット x までのセル |
| -x | 左側にオフセット x までのセル |
| {x} | 右側にオフセット x のセル |
| {-x} | 左側にオフセット x のセル |
| {x1,x2} | オフセット x1 から x2 までのセル |
| {x1,x2,dx} | x1, x1+dx, … のセル |
{{a1,a2,…},blist}のような初期条件を与えると,CellularAutomatonは常に,あたかも無限のセルがあるかのように効果的にセルオートマトンを行う.{x1,x2}のような specx を使うことで,CellularAutomatonに x1から x2までの特定のオフセットのセルだけを出力に含むように指示することができる.CellularAutomatonはデフォルトにより背景 blist と同じ値に留まらない程度に十分に離れたセルを含む.
一般に,領域 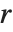 のセルオートマトンのルールが与えられると,両側に
のセルオートマトンのルールが与えられると,両側に 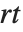 の距離のセルは原則としてシステムの進化に影響される.specx をAllとするとすべてのセルが含まれる.デフォルト設定のAutomaticの場合は値が事実上 blist と同じ値に留まるセルはカットされる.
の距離のセルは原則としてシステムの進化に影響される.specx をAllとするとすべてのセルが含まれる.デフォルト設定のAutomaticの場合は値が事実上 blist と同じ値に留まるセルはカットされる.
CellularAutomatonは任意次数に直接一般化される.しかし一般規則の規則表の項目数は天文学的に増えるので,上の2つの次数ではtotalisticやその他の特別な規則の方が有効である.
関連するガイド
-
▪
- 統計的データ解析 ▪
- 記述統計 ▪
- 確率・統計 ▪
- パラメトリック統計分布 ▪
- 離散一変量分布 ▪
- 距離と類似度の測定基準 ▪
- 数値データ ▪
- 統計モデル解析 ▪
- 曲線のフィットと近似の関数