数据中的数值运算
| Mean[list] |
均值 (平均值)
|
| Median[list] |
中位数 (中值)
|
| Max[list] | 最大值 |
| Variance[list] | 方差 |
| StandardDeviation[list] | 标准差 |
| Quantile[list,q] | q 次分位数 |
| Total[list] | 总和 |
中位数 Median[list] 给我们提供了在有序化列表 list 中寻找中间点数值的有效方法. 通常情况下,因为这种方法较少地依赖于异常点或孤立点,所以我们认为这是一种比均值来说对分布中心更稳健的度量方法.
然而,在应用中,我们还有其他10种对中位数的不同定义方法, 所有这些方法都有可能产生一些稍微不同的结果. Wolfram 语言通过以 Quantile[list,q,{{a,b},{c,d}}] 的形式引进4个中位数参数. 参数  和
和 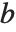 有效地定义了在整个列表中应该被认为是
有效地定义了在整个列表中应该被认为是 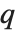 分比的位置. 如果这对应于一个整数位置, 那么在该位置的元素被认为是
分比的位置. 如果这对应于一个整数位置, 那么在该位置的元素被认为是 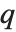 分位数. 如果这不是一个整数位, 那么我们就要采用两边元素的线性组合, 正如
分位数. 如果这不是一个整数位, 那么我们就要采用两边元素的线性组合, 正如  和
和 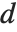 给我们描述的信息一样.
给我们描述的信息一样.
| {{0,0},{1,0}} |
逆累积分布函数 (默认)
|
| {{0,0},{0,1}} |
线性插值方法 (California 方法)
|
| {{1/2,0},{0,0}} | 在排号里最接近 |
| {{1/2,0},{0,1}} |
线性插值方法 (水文方法)
|
| {{0,1},{0,1}} |
基于均值的估计 (Weibull 方法)
|
| {{1,-1},{0,1}} | 基于众数的估计 |
| {{1/3,1/3},{0,1}} | 基于中位数的估计 |
| {{3/8,1/4},{0,1}} | 正态分布估计 |
任何时候当  , 第
, 第 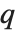 次分位数总是等于在 list 里的一些实际元素, 因此当
次分位数总是等于在 list 里的一些实际元素, 因此当  变化时,我们得到的结果总是不连续地变化. 当
变化时,我们得到的结果总是不连续地变化. 当  , 第
, 第 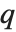 次分位数在 list 的连续元素中线性插入.在我们的定义中,中位数 Median 就采用这样的插值方法.
次分位数在 list 的连续元素中线性插入.在我们的定义中,中位数 Median 就采用这样的插值方法.
描述统计学研究分布的性质, 比如中心位置, 散布范围, 和分布形状. 我们在这里所介绍的函数可以用来做数据列表的描述性统计分析. 你可以利用 "连续分布" 和 "离散分布" 里介绍的函数来计算各种已知分布的一些标准描述性统计信息.
| Mean[data] | 平均值 |
| Median[data] |
中位数 (中值)
|
| Commonest[data] | 具有最高出现频率的元素列表 |
| GeometricMean[data] | 几何平均数 |
| HarmonicMean[data] | 调和平均数 |
| RootMeanSquare[data] | 均方根 |
| TrimmedMean[data,f] | 当一部分 |
| TrimmedMean[data,{f1,f2}] | 当 |
| Quantile[data,q] | |
| Quartiles[data] | list 里第 |
位置统计量描述了数据的位置. 最常见的功能包括集中趋势的测量, 比如均值, 中位数, 和众数. Quantile[data,q] 给我们提供了分布中达到百分之  的数据之前的位置. 换言之, Quantile 提供了
的数据之前的位置. 换言之, Quantile 提供了  的值, 并使概率
的值, 并使概率  小于或等于
小于或等于  , 而且概率
, 而且概率  大于或等于
大于或等于 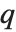 .
.
这是当列表中最小的项被排除后得到的均值. TrimmedMean 让你可以描述排除了异常值的数据:
| Variance[data] | 方差的无偏估计, |
| StandardDeviation[data] | 标准差的无偏估计 |
| MeanDeviation[data] | 平均绝对偏差, |
| MedianDeviation[data] | 中位数绝对偏差, |
| InterquartileRange[data] | 第一和第三四分位数之间的差距 |
| QuartileDeviation[data] | 四分位间距的一半 |
| Covariance[v1,v2] | 列表 v1 和 v2 之间的协方差系数 |
| Covariance[m] | 矩阵 m 的协方差矩阵 |
| Covariance[m1,m2] | 矩阵 m1 和 m2 的协方差矩阵 |
| Correlation[v1,v2] | 列表 v1 和 v2 的相关系数 |
| Correlation[m] | 矩阵 m 的相关系数矩阵 |
| Correlation[m1,m2] | 矩阵 m1 和 m2 的相关系数矩阵 |
协方差是方差的多元化扩展. 对于两个长度相等的向量来说,协方差是一个数值. 对于一个单矩阵 m 来说,协方差矩阵的第 i,j 个元素是 m 的第 i 列和第 j 列之间的协方差. 对于两个矩阵 m1 和 m2 来说,协方差矩阵的第 i,j 个元素是 m1 的第 i 列和 m2 的第j 列之间的协方差.
协方差测量散布程度, 而相关系数测量相互关系. 两个向量之间的相关系数等于向量之间的协方差除以这些向量的标准差. 同样, 相关系数矩阵的元素等于相应的协方差矩阵的元素用适当的列标准差进行尺度化后得到的结果.
| CentralMoment[data,r] | r 阶中心矩 |
| Skewness[data] | 偏度系数 |
| Kurtosis[data] | 峰度系数 |
| QuartileSkewness[data] | 四分偏度系数 |
Skewness 通过把三阶中心矩除以总体标准差的立方来计算. Kurtosis 由四阶中心矩除以数据总体方差的平方计算, 就等于 CentralMoment[data,2]. (总体方差就是二阶中心矩, 而总体标准差就是其平方根.)
| Expectation[f[x],xlist] | 函数 f 的期望值,自变量 x 是关于 list 中的数值 |
以下是数据的 Log 的期望值:
我们在此所描述的函数是最常用的离散单变量统计分布. 您可以计算它们的密度、均值、方差和其他性质. 这些分布本身采用形如 name[param1,param2,…] 的符号来表示. 函数如 Mean,给我们提供了统计分布的性质,并把分布的符号表达式作为参数. "连续分布" 描述了许多连续统计分布.
| BernoulliDistribution[p] | 均值为 p 的贝努利分布 |
| BetaBinomialDistribution[α,β,n] | 成功概率是服从 BetaDistribution[α,β] 的随机变量的二项分布 |
| BetaNegativeBinomialDistribution[α,β,n] | |
成功概率是服从 BetaDistribution[α,β] 的随机变量的负二项分布 | |
| BinomialDistribution[n,p] | n 次试验,每次试验成功概率为 p 的二项分布 |
| DiscreteUniformDistribution[{imin,imax}] | |
在范围从 imin 到 imax 的整数区间里的离散均匀分布 | |
| GeometricDistribution[p] | 每次试验成功概率为 p ,在达到第一次成功之前的试验数目所服从的几何分布 |
| HypergeometricDistribution[n,nsucc,ntot] | |
在大小为 ntot 的总体中,n 次试验有 nsucc 次成功的超几何分布 | |
| LogSeriesDistribution[θ] | 参数为 θ 的对数级数分布 |
| NegativeBinomialDistribution[n,p] | 具有参数 n 和 p 的负二项分布 |
| PoissonDistribution[μ] | 均值为 μ 的泊松分布 |
| ZipfDistribution[ρ] | 参数为 ρ 的齐夫分布 |
负二次项分布 NegativeBinomialDistribution[n,p] 给出在试验序列中 n 次成功出现之前失败次数的分布,其中每次试验成功的概率是 p. 该分布是针对任何正值 n 定义的,此处我们把 n 解释为成功的次数,并且如果 n 不是整数的话,p 作为成功的概率也将不再成立.
贝塔二项分布 BetaBinomialDistribution[α,β,n] 是二项分布和贝塔分布的合成. 一个 BetaBinomialDistribution[α,β,n] 随机变量服从 BinomialDistribution[n,p] 分布,其中成功概率 p 本身服从贝塔分布 BetaDistribution[α,β]. 贝塔负二项分布 BetaNegativeBinomialDistribution[α,β,n] 表示了类似的贝塔分布和负二项分布的合成.
齐夫分布 ZipfDistribution[ρ],有时被称为泽塔分布,首先使用在语言学界,而后其应用已经扩展到了对罕见事件的建模.
| PDF[dist,x] | 自变量为 x 的概率密度函数 |
| CDF[dist,x] | 自变量为 x 的累积分布函数 |
| InverseCDF[dist,q] | |
| Quantile[dist,q] | q 次分位数 |
| Mean[dist] | 均值 |
| Variance[dist] | 方差 |
| StandardDeviation[dist] | 标准差 |
| Skewness[dist] | 偏度系数 |
| Kurtosis[dist] | 峰度系数 |
| CharacteristicFunction[dist,t] | 特征函数 |
| Expectation[f[x],xdist] | 当 x 服从分布 dist 时,f[x] 的期望值 |
| Median[dist] | 中位数 |
| Quartiles[dist] | dist 的第 |
| InterquartileRange[dist] | 第一和第三四分位数之间的差距 |
| QuartileDeviation[dist] | 四分位间距的一半 |
| QuartileSkewness[dist] | 四分偏度系数的测量 |
| RandomVariate[dist] | 指定分布的伪随机数 |
| RandomVariate[dist,dims] | 维度为 dims,并且元素服从指定分布的伪随机数组 |
分布以符号表达式来表示. 如果 x 是一个数值,PDF[dist,x] 提供了在 x 点的密度函数,否则的话,只要有可能我们就保留函数的符号表达式形式. 相同地,CDF[dist,x] 给出累积分布函数而 Mean[dist] 给出指定分布的均值. 为了更全面地描述统计分布的不同函数,请参见 "连续分布" 里类似的关于连续分布的介绍.
我们这里所描述的函数是在连续性的单变量统计分布里最常用的一些函数. 您可以计算它们的密度、均值、方差、和其他相关的属性. 这些分布本身可以采用形如 name[param1,param2,…] 的符号来表示. 函数如 Mean,可以给我们提供统计分布的性质,并且使用分布的符号表达式作为一个参数. "离散分布" 描述了许多常见的离散单变量统计分布.
| NormalDistribution[μ,σ] | 具有均值 μ 和标准差 σ 的正态(高斯)分布 |
| HalfNormalDistribution[θ] | 尺度和参数 θ 成反比的半正态分布 |
| LogNormalDistribution[μ,σ] | 均值为 μ,标准差为 σ 的对数正态分布 |
| InverseGaussianDistribution[μ,λ] | 具有均值 μ 和尺度 λ 的逆高斯分布 |
对数正态分布 LogNormalDistribution[μ,σ] 是正态分布的随机变量的指数服从的分布. 当许多独立的随机变量以相乘的方式被组合时出现该分布. 半正态分布 HalfNormalDistribution[θ] 和局限于域  的分布 NormalDistribution[0,1/(θ Sqrt[2/π])] 成正比 .
的分布 NormalDistribution[0,1/(θ Sqrt[2/π])] 成正比 .
逆高斯分布(InverseGaussianDistribution[μ,λ]),有时被称为森林分布(Wald distribution),是有正漂移的布朗运动的首达时分布.
| ChiSquareDistribution[ν] | ν 个自由度的 |
| InverseChiSquareDistribution[ν] | 具有自由度 ν 的逆 |
| FRatioDistribution[n,m] | 分子为 n,分母为 m 的 |
| StudentTDistribution[ν] | 具有 ν 个自由度的学生 t 分布 |
| NoncentralChiSquareDistribution[ν,λ] | 具有自由度 ν 和非中心化参数 λ 的非中心卡方分布( |
| NoncentralStudentTDistribution[ν,δ] | 具有自由度 ν 和非中心化参数 δ 的学生 t 分布 |
| NoncentralFRatioDistribution[n,m,λ] | 分子自由度为 n 和分母自由度为 m 的非中心化 |
如果 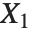 , …,
, …, 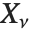 是独立的正态随机变量,其方差为1,均值为0,那么
是独立的正态随机变量,其方差为1,均值为0,那么  服从一个自由度为
服从一个自由度为 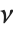 的
的 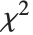 分布 . 如果一个正态变量通过减去它的均值,并除以标准差来标准化,那么这样的数值结果的平方和服从该分布.
分布 . 如果一个正态变量通过减去它的均值,并除以标准差来标准化,那么这样的数值结果的平方和服从该分布.  分布被广泛用于描述正态样本的方差.
分布被广泛用于描述正态样本的方差.
如果 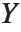 服从一个自由度为
服从一个自由度为 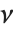 的
的  分布,
分布,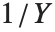 服从逆
服从逆 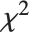 分布 InverseChiSquareDistribution[ν]. 一个自由度为
分布 InverseChiSquareDistribution[ν]. 一个自由度为 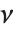 和尺度为
和尺度为  的尺度化的逆
的尺度化的逆 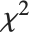 分布 可以由 InverseChiSquareDistribution[ν,ξ] 给出. 逆
分布 可以由 InverseChiSquareDistribution[ν,ξ] 给出. 逆 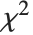 分布通常用作正态分布样本的贝叶斯分析中的方差的先验分布.
分布通常用作正态分布样本的贝叶斯分析中的方差的先验分布.
一个服从学生 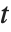 分布 的变量也可以写为一个正态随机变量的函数. 假设
分布 的变量也可以写为一个正态随机变量的函数. 假设 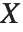 和
和 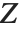 是独立的随机变量,其中
是独立的随机变量,其中 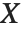 是一个标准正态分布,而
是一个标准正态分布,而  是一个自由度为
是一个自由度为 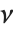 的
的  变量. 在这种情况下,
变量. 在这种情况下, 服从自由度为
服从自由度为 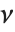 的
的 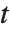 分布. 学生
分布. 学生 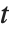 分布关于纵轴对称, 并且表示一个正态变量和它的标准差之间的比率的特点. 定位参数和尺度参数可以包括在 StudentTDistribution[μ,σ,ν] 里,并且用 μ 和 σ 来表示. 当
分布关于纵轴对称, 并且表示一个正态变量和它的标准差之间的比率的特点. 定位参数和尺度参数可以包括在 StudentTDistribution[μ,σ,ν] 里,并且用 μ 和 σ 来表示. 当  ,
,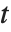 分布和柯西分布( Cauchy distribution) 一样.
分布和柯西分布( Cauchy distribution) 一样.
方差为  和均值非零的
和均值非零的 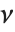 个正态分布的随机变量的平方和服从一个非中心化
个正态分布的随机变量的平方和服从一个非中心化  分布NoncentralChiSquareDistribution[ν,λ]. 非中心化参数
分布NoncentralChiSquareDistribution[ν,λ]. 非中心化参数  是随机变量的均值的平方和. 注意,在我们的文档的不同地方,
是随机变量的均值的平方和. 注意,在我们的文档的不同地方, 或
或 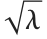 被作为非中心化参数.
被作为非中心化参数.
非中心化学生  分布 NoncentralStudentTDistribution[ν,δ] 描述了比率
分布 NoncentralStudentTDistribution[ν,δ] 描述了比率 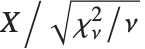 ,其中
,其中 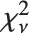 是一个自由度为
是一个自由度为  的中心随机变量
的中心随机变量 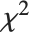 ,而
,而  是一个方差为
是一个方差为  和均值为
和均值为  的独立正态分布的随机变量.
的独立正态分布的随机变量.
非中心化  ‐比率 分布 NoncentralFRatioDistribution[n,m,λ] 是
‐比率 分布 NoncentralFRatioDistribution[n,m,λ] 是  对
对 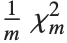 比率的分布,其中
比率的分布,其中 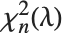 是一个非中心化参数为
是一个非中心化参数为  和自由度为
和自由度为 的非中心化
的非中心化 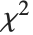 随机变量,而
随机变量,而 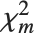 是一个自由度为
是一个自由度为  的中心化
的中心化 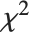 随机变量.
随机变量.
| TriangularDistribution[{a,b}] | 区间在 {a,b} 上的对称三角分布 |
| TriangularDistribution[{a,b},c] | 区间为 {a,b},最大值为 c 的三角分布 |
| UniformDistribution[{min,max}] | 区间在 {min,max} 上的均匀分布 |
三角分布 TriangularDistribution[{a,b},c] 是区间 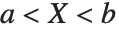 上的三角分布,其最大概率值为
上的三角分布,其最大概率值为 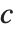 并且满足
并且满足 . 如果
. 如果  是
是 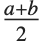 ,TriangularDistribution[{a,b},c] 是对称三角分布 TriangularDistribution[{a,b}].
,TriangularDistribution[{a,b},c] 是对称三角分布 TriangularDistribution[{a,b}].
均匀分布 UniformDistribution[{min,max}], 通常称为矩形分布, 它的特点是它的随机变量的值在每个位置都有相同的概率.我们常见的一个均匀分布随机变量的例子是在一条范围从 min 到 max 的线上随机选择的点的位置.
| BetaDistribution[α,β] | 形状参数为 α 和 β 的连续贝塔分布 |
| CauchyDistribution[a,b] | 具有定位参数 a 和尺度参数 b 的柯西分布 |
| ChiDistribution[ν] | ν 个自由度的 |
| ExponentialDistribution[λ] | 尺度参数和 λ 成反比的指数分布 |
| ExtremeValueDistribution[α,β] | 具有定位参数 α 和尺度参数 β 的极大值 (Fisher–Tippett) 分布 |
| GammaDistribution[α,β] | 具有形状参数 α 和尺度参数 β 的伽马分布 |
| GumbelDistribution[α,β] | 具有定位参数 α 和尺度参数 β 的冈贝尔极小值分布 |
| InverseGammaDistribution[α,β] | 具有形状参数 α 和尺度参数 β 的逆伽马分布 |
| LaplaceDistribution[μ,β] | 均值为 μ,尺度参数为 β 的拉普拉斯(双指数)分布 |
| LevyDistribution[μ,σ] | 具有定位参数 μ 和扩散参数 σ 的列维(Lévy)分布 |
| LogisticDistribution[μ,β] | 均值为 μ, 尺度参数为 β 的洛杰斯蒂克分布 |
| MaxwellDistribution[σ] | 尺度参数为 σ 的Maxwell (Maxwell–Boltzmann) 分布 |
| ParetoDistribution[k,α] | 具有最小值参数 k 和形状参数 α 的 Pareto 分布 |
| RayleighDistribution[σ] | 尺度参数为 σ 的瑞利分布 |
| WeibullDistribution[α,β] | 形状参数为 α 和尺度参数为 β 的威布尔分布 |
当  并且
并且  ,伽马分布 GammaDistribution[α,λ] 描述了
,伽马分布 GammaDistribution[α,λ] 描述了 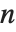 个单位的正态随机变量的平方和的分布. 这种类型的伽马分布被称为具有
个单位的正态随机变量的平方和的分布. 这种类型的伽马分布被称为具有 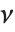 个自由度的
个自由度的  分布. 当
分布. 当  ,伽马分布以指数分布 的形式出现ExponentialDistribution[λ],并且经常用以描述事件之间的等待时间.
,伽马分布以指数分布 的形式出现ExponentialDistribution[λ],并且经常用以描述事件之间的等待时间.
如果一个随机变量 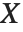 服从伽马分布 GammaDistribution[α,β],
服从伽马分布 GammaDistribution[α,β],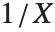 服从逆伽马分布 InverseGammaDistribution[α,1/β]. 如果一个随机变量
服从逆伽马分布 InverseGammaDistribution[α,1/β]. 如果一个随机变量 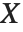 服从 InverseGammaDistribution[1/2,σ/2],
服从 InverseGammaDistribution[1/2,σ/2], 服从 Lévy 分布 LevyDistribution[μ,σ].
服从 Lévy 分布 LevyDistribution[μ,σ].
拉普拉斯分布 LaplaceDistribution[μ,β] 是两个服从相同的指数分布的独立的随机变量的差值的分布. 当一个长尾分布是比较理想的分布时,洛杰斯蒂克分布 LogisticDistribution[μ,β]经常被用来代替正态分布.
威布尔分布 WeibullDistribution[α,β] 通常用于工程上描述一个对象的生命期. 极值分布 ExtremeValueDistribution[α,β] 是服从不同分布的大样本中的最大值的限制性分布,包括正态分布. 在这样的样本中最小值的限制性分布是冈贝尔分布,GumbelDistribution[α,β]. “极值”和“冈贝尔分布”这两个名字有时可以交替使用,因为最大和最小极值的分布由一个服从线性变化的变量相关. 极值分布有时也被称为对数-威布尔分布,因为在一个服从极值分布的随机变量和一个妥善偏移和尺度化的服从威布尔分布的随机变量之间存在对数关系.
| PDF[dist,x] | 概率密度函数,自变量为 x |
| CDF[dist,x] | 累积分布函数,自变量为 x |
| InverseCDF[dist,q] | |
| Quantile[dist,q] | q 次分位数 |
| Mean[dist] | 均值 |
| Variance[dist] | 方差 |
| StandardDeviation[dist] | 标准差 |
| Skewness[dist] | 偏度系数 |
| Kurtosis[dist] | 峰度系数 |
| CharacteristicFunction[dist,t] | 特征函数 |
| Expectation[f[x],xdist] | 当 x 服从分布 dist 时,f[x] 的期望值 |
| Median[dist] | 中位数 |
| Quartiles[dist] | dist 的第 |
| InterquartileRange[dist] | 第一和第三四分位数之间的差距 |
| QuartileDeviation[dist] | 四分位间距的一半 |
| QuartileSkewness[dist] | 四分偏度系数的测量 |
| RandomVariate[dist] | 服从指定分布的伪随机数 |
| RandomVariate[dist,dims] | 维度为 dims 并且元素服从指定分布的伪随机数组 |
在点  的累积分布函数(CDF)由分布的概率密度函数(PDF)直到点
的累积分布函数(CDF)由分布的概率密度函数(PDF)直到点 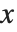 的积分给出. 因此,概率密度函数可以由对累积分布函数求导得到(可能在广义意义上). 在该软件包中,概率分布由符号化的形式表示. 如果
的积分给出. 因此,概率密度函数可以由对累积分布函数求导得到(可能在广义意义上). 在该软件包中,概率分布由符号化的形式表示. 如果  是一个数值型数据, PDF[dist,x] 计算在点
是一个数值型数据, PDF[dist,x] 计算在点 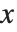 处的密度,否则,函数就保留符号化表达式的形式. 同样地,CDF[dist,x] 给出了累积分布.
处的密度,否则,函数就保留符号化表达式的形式. 同样地,CDF[dist,x] 给出了累积分布.
逆累积分布函数 InverseCDF[dist,q] 提供了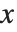 点的值,在该点 CDF[dist,x] 达到
点的值,在该点 CDF[dist,x] 达到 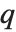 . 中位数由InverseCDF[dist,1/2] 给出. 四分位数、十分位数和百分位数是逆累积分布函数的特殊值. 四分位数的偏度等于
. 中位数由InverseCDF[dist,1/2] 给出. 四分位数、十分位数和百分位数是逆累积分布函数的特殊值. 四分位数的偏度等于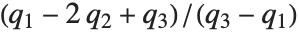 ,此处
,此处 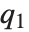 、
、 和
和 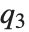 分别是第一,第二和第三四分位数. 逆累积分布函数用于构建统计参数的置信区间. 对于连续分布,InverseCDF[dist,q] 和 Quantile[dist,q] 是相等的.
分别是第一,第二和第三四分位数. 逆累积分布函数用于构建统计参数的置信区间. 对于连续分布,InverseCDF[dist,q] 和 Quantile[dist,q] 是相等的.
均值 Mean[dist] 是服从 dist 分布的随机变量的期望值,经常可以表示为 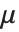 . 均值由
. 均值由 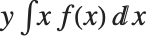 给出,其中
给出,其中 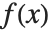 是分布的概率密度函数. 方差 Variance[dist] 由
是分布的概率密度函数. 方差 Variance[dist] 由 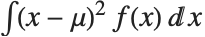 给出. 方差的平方根被称为标准差,通常用
给出. 方差的平方根被称为标准差,通常用  表示.
表示.
RandomVariate[dist] 给出服从指定分布的伪随机数字.
下面是累积分布函数. 它由内置函数 GammaRegularized 给出:
聚类分析是一种用于数据分类的无监督学习技术. 数据元素被划分为称为簇 (clusters) 的组,它们代表了基于距离或者差异函数的邻近元素组成的集合. 相同元素组成的对的距离或相异度为零,而其他所有元素对的距离或者相异度都为正值.
| FindClusters[data] | 把 data 划分为相似元素组成的列表 |
| FindClusters[data,n] | 把 data 划分为相似元素组成的最多 n 个列表 |
FindClusters 的数据参数可以是数据元素列表、关联、或者对元素和标签进行索引的规则列表.
| {e1,e2,…} | 指定为数据元素 ei 的列表的数据 |
| {e1v1,e2v2,…} | 指定作为数据元素 ei 和标签 vi 之间的规则列表的数据 |
| {e1,e2,…}{v1,v2,…} | 指定为数据元素 ei 到标签 vi 的映射规则的数据 |
| key1e1,key2e2…> | 指定为把数据元素 ei 映射到标签 keyi 的关联的数据 |
在 FindClusters 中指定数据的方式.
FindClusters 基于数字的邻近度进行聚类划分:
在默认设置下,FindClusters 已经求得了由点组成的4个簇.
用户也可以命令 FindClusters 寻找指定数目的簇.
选项名
|
默认值
| |
| CriterionFunction | Automatic | 选择方法的准则 |
| DistanceFunction | Automatic | 采用的距离函数 |
| Method | Automatic | 采用的聚类方法 |
| PerformanceGoal | Automatic | 要优化的性能方面 |
| Weights | Automatic | 每个样本要给予多少权重 |
FindClusters 的选项.
FindClusters[{e1,e2,…},DistanceFunction->f] 把元素对作为较不相似来处理,当它们之间的距离 f[ei,ej] 较大时. 函数 f 可以是任意适当的距离或者相异函数. 相异函数 f 满足如下条件:
如果 ei 是数字向量,默认情况下 FindClusters 使用平方欧氏距离. 如果 ei 是布尔值 True 和 False (或者 0 和1)元素组成的列表,默认情况下 FindClusters 采用基于不相似元素的规范化的分式而得到的相异度度量. 如果 ei 是字符串,默认情况下 FindClusters 采用基于从一个字符串变为另一个所需的点的改变数目而得到的距离函数.
| EuclideanDistance[u,v] | 欧氏范数 |
| SquaredEuclideanDistance[u,v] | 平方欧氏范数 |
| ManhattanDistance[u,v] | 曼哈顿距离 |
| ChessboardDistance[u,v] | 棋盘或者切比雪夫距离 |
| CanberraDistance[u,v] | 堪培拉距离 |
| CosineDistance[u,v] | 余弦距离 |
| CorrelationDistance[u,v] | |
| BrayCurtisDistance[u,v] | 布雷-柯蒂斯距离 |
布尔向量之间的相异度通常由成对比较布尔向量 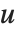 和
和  的元素计算得出. 关于
的元素计算得出. 关于 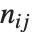 总结每个相异函数是很方便的,其中
总结每个相异函数是很方便的,其中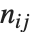 是在
是在 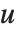 和
和  中的相应元素对的数目,并且分别等于
中的相应元素对的数目,并且分别等于 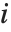 和
和 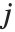 . 数值
. 数值 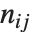 计算
计算 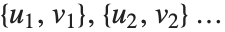 中的
中的  对,其中
对,其中  和
和 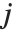 或者是 0 或者是 1. 如果布尔值是 True 和 False,True 相当于 1,而 False 相当于 0.
或者是 0 或者是 1. 如果布尔值是 True 和 False,True 相当于 1,而 False 相当于 0.
| MatchingDissimilarity[u,v] | 简单匹配 (n10+n01)/Length[u] |
| JaccardDissimilarity[u,v] | 雅卡尔相异度 |
| RussellRaoDissimilarity[u,v] | 罗素-饶相异度 (n10+n01+n00)/Length[u] |
| SokalSneathDissimilarity[u,v] | 索卡尔-斯尼思相异度 |
| RogersTanimotoDissimilarity[u,v] | Rogers–Tanimoto 相异度 |
| DiceDissimilarity[u,v] | Dice 相异度 |
| YuleDissimilarity[u,v] | Yule 相异度 |
| EditDistance[u,v] | 把 u 转换为字符串 v 的编辑次数 |
| DamerauLevenshteinDistance[u,v] | u 和 v 之间的 Damerau–Levenshtein 距离 |
| HammingDistance[u,v] | 在 u 和 v 中不相同的元素数目 |
编辑距离通过计算当保持字符顺序、并把一个字符串转换为另一个字符串的同时,所要进行的删除、插入和替换的次数. 相比之下,Damerau–Levenshtein 距离计算删除、插入、替换和换位的次数,而汉明距离只计算替换的次数.
Method 选项可以用来指定聚类所用的不同方法.
| "Agglomerate" | 层次化地寻找分类 |
| "Optimize" | 通过局部优化寻找分类 |
| "DBSCAN" | 具有噪声的基于密度的空间聚类方法 |
| "GaussianMixture" | 变化的高斯混合算法 |
| "JarvisPatrick" | Jarvis–Patrick 聚类算法 |
| "KMeans" | k-平均聚类算法 |
| "KMedoids" | 围绕中心点划分 |
| "MeanShift" | 平均移动聚类算法 |
| "NeighborhoodContraction" | 将数据点移向高密度区域 |
| "SpanningTree" | 基于最小生成树的聚类算法 |
| "Spectral" | 谱聚类算法 |
Method 选项的明确设置.
默认情况下,FindClusters 会尝试不同的方法然后选择最好的聚类划分.
"DBSCAN"、"JarvisPatrick"、"MeanShift"、"SpanningTree"、 "NeighborhoodContraction" 和 "GaussianMixture" 方法决定了如何把数据聚类划分而不假设特定的聚类数目.
| "NeighborhoodRadius" | 指定一点邻域的平均半径 |
| "NeighborsNumber" | 指定邻域中点的平均数目 |
| "InitialCentroids" | 指定初始的质心/中心点 |
| "SharedNeighborsNumber" | 指定邻域的最小数目 |
| "MaxEdgeLength" | 指定修正长度临界值 |
| ClusterDissimilarityFunction | 指定簇之间的相异性 |
子选项 "NeighborhoodRadius" 可用在方法 "DBSCAN"、"MeanShift"、"JarvisPatrick"、"NeighborhoodContraction" 和 "Spectral" 中.
| "Single" | 最小簇间相异度 |
| "Average" | 平均簇间相异度 |
| "Complete" | 最大簇间相异度 |
| "WeightedAverage" | 加权平均簇间相异度 |
| "Centroid" | 与簇中心的距离 |
| "Median" | 与簇中位数的距离 |
| "Ward" | Ward 最小方差相异度 |
| f | 纯函数 |
ClusterDissimilarityFunction 子选项的可能值.
设置 ClusterDissimilarityFunction->f 下,f 是定义链接算法的纯函数. 簇之间的距离或者相异度由未合并的簇之间的距离或者相异度的信息来递归决定,并以此产生和新合并成的簇之间的距离和相异度信息. 函数 f 定义从簇 k 到由簇 i 和 j 融合形成的新簇之间的距离. 给 f 提供的自变量为 dik、djk、dij、ni、nj 和 nk,其中 d 是簇之间的距离,而 n 是一个簇中的元素数目.
CriterionFunction 选项既可用于选择采用的方法,也可用于选择簇的最佳数量.
| "StandardDeviation" | 均方根标准差 |
| "RSquared" | R-平方 |
| "Dunn" | Dunn 索引 |
| "CalinskiHarabasz" | Calinski–Harabasz 索引 |
| "DaviesBouldin" | Davies–Bouldin 索引 |
| Automatic | 内部索引 |
以下显示了用不同的 CriterionFunction 设置得到的聚类结果:
以下是使用默认的 CriterionFunction 设置自动选择簇的数目而求得的簇:
Nearest 用来在一个列表中寻找与给定数据点最接近的元素.
| Nearest[{elem1,elem2,…},x] | 给出与 x 最接近的 elemi 的列表 |
| Nearest[{elem1->v1,elem2->v2,…},x] | |
给出与 x 最接近的对应于 elemi 的 vi | |
| Nearest[{elem1,elem2,…}->{v1,v2,…},x] | |
给出相同的结果 | |
| Nearest[{elem1,elem2,…}->Automatic,x] | |
vi 取值为整数 1, 2, 3, … | |
| Nearest[data,x,n] | 给出与 x 最接近的 n 个元素 |
| Nearest[data,x,{n,r}] | 给出在半径 r 内,与 x 最接近的 n 个元素 |
| Nearest[data] | 产生可以重复应用于不同 x 的 NearestFunction[…] |
Nearest 函数.
Nearest 对于数值列表,张量或者字符串列表适用.
以下在二维空间内产生 10,000 个点的集合,以及 NearestFunction:
如果不使用 NearestFunction,则需要花费更长的时间:
选项名
|
默认值
| |
| DistanceFunction | Automatic | 使用的距离度量 |
Nearest 的选项.
| Fit[{y1,y2,…},{f1
,
f2,…},x] | 用 fi 的线性组合拟合数据 yn |
| Fit[{{x1,y1},{x2,y2},…},{f1
,
f2,…},x] | 用 fi 的线性组合拟合一组点 (xn,yn) |
| FindFit[data,form,{p1,p2,…},x] | 使用参数 pi 寻找 form 的拟合 |
| Fourier[data] | 数值傅立叶变换 |
| InverseFourier[data] | 数值傅立叶逆变换 |
在许多情况下,用户可能想要找到对给定数据集达到最佳拟合的公式. 在 Wolfram 语言中要实现这一目的一种方法是使用 Fit.
| Fit[{f1,f2,…},{fun1,fun2,…},x] | 寻找 funi 的线性组合,使之对 fi 达到最优拟合 |
| {f1,f2,…} | 单自变量取值为 |
| {{x1,f1},{x2,f2},…} | 单自变量取值为 |
| {{x1,y1,…,f1},{x2,y2,…,f2},…} | 自变量取值为 |
| Fit[data,{fun1,fun2,…},{x,y,…}] | 对多变量函数进行拟合 |
Fit 采用函数列表,并且使用确定并且有效的步骤来找到产生最佳二乘拟合的函数线性组合. 然而,有时候,用户可能想要找到不只包括指定函数线性组合的非线性拟合. 这可以使用 FindFit 实现,它采用任何形式的函数,并且搜索产生数据最佳拟合的参数值.
| FindFit[data,form,{par1,par2,…},x] | 寻找使得 form 对 data 达到最佳拟合的 pari 的值 |
| FindFit[data,form,pars,{x,y,…}] | 多变量数据拟合 |
该结果与 Fit 所得结果相同:
以下使用的是非线性形式拟合,并不能由 Fit 处理:
默认情况下,Fit 和 FindFit 产生最小二乘拟合,我们定义它来最小化 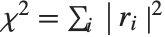 的值,其中
的值,其中  是给定每个原始数据点和拟合值的差异下的残差. 然而,用户也能基于其他范数考虑拟合. 如果用户设置选项 NormFunction->u,那么FindFit 将试图找到最小化 u[r] 的值的拟合,其中 r 是残差列表. 默认为 NormFunction->Norm,对应于最小二乘拟合.
是给定每个原始数据点和拟合值的差异下的残差. 然而,用户也能基于其他范数考虑拟合. 如果用户设置选项 NormFunction->u,那么FindFit 将试图找到最小化 u[r] 的值的拟合,其中 r 是残差列表. 默认为 NormFunction->Norm,对应于最小二乘拟合.
FindFit 首先寻找产生最佳拟合的参数值. 有时候,用户可能要告诉系统从什么位置开始搜索. 用户可以通过给出  形式的参数实现. FindFit 也为用户提供了多种选项设置,以便用户控制如何进行搜索.
形式的参数实现. FindFit 也为用户提供了多种选项设置,以便用户控制如何进行搜索.
选项名
|
默认值
| |
| NormFunction | Norm | 采用的范数 |
| AccuracyGoal | Automatic | 试图获得的准确度的位数 |
| PrecisionGoal | Automatic | 试图获得的精度的位数 |
| WorkingPrecision | Automatic | 在内部计算中采用的精度 |
| MaxIterations | Automatic | 采用的最大迭代次数 |
| StepMonitor | None | 在每一步中所计算的表达式 |
| EvaluationMonitor | None | 当计算 form 时,所计算的表达式 |
| Method | Automatic | 使用的方法 |
FindFit 的选项.
当我们对数据进行模型拟合时,分析模型对数据拟合的好坏以及检验该拟合是否满足模型的假设条件都是非常有必要的. 在 Wolfram 系统里,对大部分常见的统计模型来说,这一工作都可以通过用于建立 FittedModel 对象的拟合函数来实现.
| FittedModel | 代表一个符号化的拟合模型 |
FittedModel 对象可以在某一点求值,或者用来对结果和诊断信息进行查询. 对于不同的模型类别,诊断方法有所不同. 现有的模型拟合函数可以用来拟合线性模型、广义线性模型和非线性模型.
| LinearModelFit | 构建一个线性模型 |
| GeneralizedLinearModelFit | 构建一个广义线性模型 |
| LogitModelFit | 构建一个二项logistic回归模型 |
| ProbitModelFit | 构建一个二项probit回归模型 |
| NonlinearModelFit | 构建一个非线性最小二乘模型 |
用来产生 FittedModel 对象的函数
诸如 LinearModelFit 的模型拟合的函数和诸如 Fit 和 FindFit 的函数之间的主要差别在于从 FittedModel 对象中方便地获取诊断信息的能力. 对相关结果,不用重新拟合模型也能访问.
我们还可以把和属性计算相关的拟合选项传递给 FittedModel 对象来重载默认值.
线性模型
假设误差服从独立的正态分布的线性模型属于我们最常见的数据模型. 这种类型的模型可以用 LinearModelFit 函数来拟合.
| LinearModelFit[{y1,y2,…},{f1,f2,…},x] | 获得一个基函数为 fi,单预测变量为 x 的线性模型 |
| LinearModelFit[{{x11,x12,…,y1},{x21,x22,…,y2}},{f1,f2,…},{x1,x2,…}] | 获得一个具有多个预测变量 xi 的线性模型 |
| LinearModelFit[{m,v}] | 获得一个基于一个设计矩阵 m 和一个响应向量 v 的线性模型 |
选项名
|
默认值
| |
| ConfidenceLevel | 95/100 | 用于参数和预测的置信水平 |
| IncludeConstantBasis | True | 是否包括一个常数基函数 |
| LinearOffsetFunction | None | 线性预测的已知偏移量 |
| NominalVariables | None | 名义或类别变量 |
| VarianceEstimatorFunction | Automatic | 用于估计误差方差的函数 |
| Weights | Automatic | 数据元素的权重 |
| WorkingPrecision | Automatic | 内部计算所用的精度 |
LinearModelFit 的选项.
Weights 选项描述了加权线性回归的权值. NominalVariables 选项用来指定哪个预测变量应该作为名义变量或分类变量来处理. 用 NominalVariables->All 时,我们所用的是方差分析模型 (ANOVA) . 用 NominalVariables->{x1,…,xi-1,xi+1,…,xn} 时,我们所用的是协方差分析模型,除了第  个预测变量外,所有的预测变量都作为名义变量处理. 名义变量在这里是用一些代表与观察到的名义分类变量值相等或不相等关系的二进制变量来表示的.
个预测变量外,所有的预测变量都作为名义变量处理. 名义变量在这里是用一些代表与观察到的名义分类变量值相等或不相等关系的二进制变量来表示的.
ConfidenceLevel、VarianceEstimatorFunction 和 WorkingPrecision 和初始拟合后的结果的计算相关. 这些选项可以在 LinearModelFit 里被设置,用以对由 FittedModel 对象所得的结果指定默认设置. 这些选项也可以在一个已经建立好的 FittedModel 对象里设置,用以重载最初赋给 LinearModelFit 的选项值.
IncludeConstantBasis、LinearOffsetFunction、NominalVariables 和 Weights 只和拟合过程相关. 在一个已经建立好的 FittedModel 对象里设置这些选项将对结果没有进一步的影响.
| "BasisFunctions" | 基函数列表 |
| "BestFit" | 拟合函数 |
| "BestFitParameters" | 参数估计 |
| "Data" | 输入数据或设计矩阵和响应向量 |
| "DesignMatrix" | 模型设计矩阵 |
| "Function" | 最佳拟合纯函数 |
| "Response" | 输入数据的响应值 |
"BestFitParameters" 属性给出拟合参数值 {β0,β1,…}. "BestFit" 是拟合函数  而 "Function" 把拟合函数指定为一个纯函数. "BasisFunctions" 给出函数
而 "Function" 把拟合函数指定为一个纯函数. "BasisFunctions" 给出函数 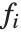 的列表,其中当模型中有常量时,
的列表,其中当模型中有常量时, 为常量1. "DesignMatrix" 是数据的设计矩阵或模型矩阵. "Response" 给出响应列表或者帮助我们从原始数据得到
为常量1. "DesignMatrix" 是数据的设计矩阵或模型矩阵. "Response" 给出响应列表或者帮助我们从原始数据得到 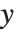 值.
值.
| "FitResiduals" | 实际响应和预测响应的差值 |
| "StandardizedResiduals" | 拟合残差除以每个残差的标准误差 |
| "StudentizedResiduals" | 拟合残差除以每个消除误差估计值 |
残差给我们提供了在拟合值和初始响应之间的点态差的度量. "FitResiduals" 给我们提供了观测值和拟合值之间的差值{y1-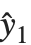 ,y2-
,y2- ,…}. "StandardizedResiduals" 和 "StudentizedResiduals" 是残差的尺度化表示. 第
,…}. "StandardizedResiduals" 和 "StudentizedResiduals" 是残差的尺度化表示. 第 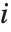 个标准化残差是
个标准化残差是  ,其中
,其中  是估计误差方差,
是估计误差方差,  是帽子矩阵的第
是帽子矩阵的第 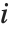 个对角线元素,而
个对角线元素,而  是第
是第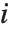 个数据点的权值. 第
个数据点的权值. 第 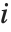 学生化残差采用同样的公式,只是把
学生化残差采用同样的公式,只是把 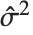 用
用 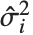 (忽略掉第
(忽略掉第 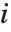 个数据点的方差估计)来替代.
个数据点的方差估计)来替代.
| "ANOVATable" | 方差分析表 |
| "ANOVATableDegreesOfFreedom" | 方差分析表(ANOVA)中的自由度 |
| "ANOVATableEntries" | 表中数值的非格式化数组表示 |
| "ANOVATableFStatistics" | 表中的 F 统计量 |
| "ANOVATableMeanSquares" | 表中的均方误差 |
| "ANOVATablePValues" | 表中的 |
| "ANOVATableSumsOfSquares" | 表中的平方和 |
| "CoefficientOfVariation" | 响应均值除以估计标准偏差 |
| "EstimatedVariance" | 误差方差估计 |
| "PartialSumOfSquares" | 当非常量基函数被删除后模型平方和的改变 |
| "SequentialSumOfSquares" | 通过分支分割得到的模型平方和 |
"ANOVATable" 给出了模型的格式化的方差分析表. "ANOVATableEntries" 给出了表中列出的数值,而另外剩下的 ANOVATable 属性给我们提供了表中的列元素,以便表的每个具体部分都可以在将来的计算中被方便地使用.
| "CorrelationMatrix" | 参数关联矩阵 |
| "CovarianceMatrix" | 参数协方差矩阵 |
| "EigenstructureTable" | 参数关联矩阵的特征结构 |
| "EigenstructureTableEigenvalues" | 表的特征值 |
| "EigenstructureTableEntries" | 表中数值的非格式化数组表示 |
| "EigenstructureTableIndexes" | 表中的指标值 |
| "EigenstructureTablePartitions" | 表中的划分 |
| "ParameterConfidenceIntervals" | 参数置信区间 |
| "ParameterConfidenceIntervalTable" | 拟合参数的置信区间信息表 |
| "ParameterConfidenceIntervalTableEntries" | 表中数值的非格式化数组表示 |
| "ParameterConfidenceRegion" | 椭圆参数置信区域 |
| "ParameterErrors" | 参数估计的标准误差 |
| "ParameterPValues" | 参数 |
| "ParameterTable" | 拟合参数信息表 |
| "ParameterTableEntries" | 表中数值的非格式化数组形式 |
| "ParameterTStatistics" | 参数估计的 |
| "VarianceInflationFactors" | 估计参数的膨胀因子列表 |
"CovarianceMatrix" 给我们提供了拟合参数之间的协方差. 相应地,矩阵是  ,这里
,这里 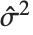 是方差估计值,
是方差估计值,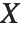 是设计矩阵,而
是设计矩阵,而  是权值的对角化矩阵. "CorrelationMatrix" 是参数估计相应的相关矩阵. "ParameterErrors" 相当于协方差矩阵对角线元素的平方根.
是权值的对角化矩阵. "CorrelationMatrix" 是参数估计相应的相关矩阵. "ParameterErrors" 相当于协方差矩阵对角线元素的平方根.
表的估计列相当于 "BestFitParameters". 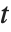 统计量是除以标准误差后得到的估计值. 每个
统计量是除以标准误差后得到的估计值. 每个 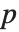 值都是
值都是  统计量的双侧
统计量的双侧 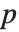 值,而且可以用以评价参数估计是否显著地不同于0. 每个置信区间给我们提供了,在由 ConfidenceLevel 选项预订的置信水平上,参数置信区间的上界和下界. 不同的 ParameterTable 和ParameterConfidenceIntervalTable 属性可以用以从表中获得列或非格式化的数值数组.
值,而且可以用以评价参数估计是否显著地不同于0. 每个置信区间给我们提供了,在由 ConfidenceLevel 选项预订的置信水平上,参数置信区间的上界和下界. 不同的 ParameterTable 和ParameterConfidenceIntervalTable 属性可以用以从表中获得列或非格式化的数值数组.
"VarianceInflationFactors" 可以用来测量基函数间的多重共线性. 第 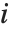 个膨胀因子相当于
个膨胀因子相当于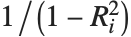 ,其中
,其中  是把第
是把第 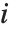 个基函数拟合成其他基函数的线性函数的变差系数. 采用 IncludeConstantBasis->True 设置时,第一个膨胀因子相应于常数项.
个基函数拟合成其他基函数的线性函数的变差系数. 采用 IncludeConstantBasis->True 设置时,第一个膨胀因子相应于常数项.
"EigenstructureTable" 给我们提供了非常数基函数的特征值,条件指标和方差划分. 指标列给我们提供了每个特征值和最大特征值之间比率的平方根. 每个基函数的列给我们提供了用相应特征向量解释的基函数中的变差比例. "EigenstructureTablePartitions" 给我们提供了表中所有基函数的方差划分值.
| "BetaDifferences" | 测量对参数值影响的 DFBETAS 度量 |
| "CatcherMatrix" | 捕集矩阵 |
| "CookDistances" | 库克距离列表 |
| "CovarianceRatios" | 测量观测值影响的 COVRATIO 度量 |
| "DurbinWatsonD" | 自相关的杜宾-瓦特森 |
| "FitDifferences" | 测量对预测值影响的 DFFITS 度量 |
| "FVarianceRatios" | 测量观测数据影响的 FVARATIO 度量 |
| "HatDiagonal" | 帽子矩阵的对角线元素 |
| "SingleDeletionVariances" | 忽略第 |
影响因子的点态度量经常被用于评价每个单独的数据点是否对拟合产生大的影响. 帽子矩阵和捕集矩阵在这样的诊断分析中扮演重要角色. 帽子矩阵是满足 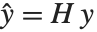 的矩阵
的矩阵 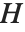 ,此处
,此处 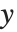 是观测到的响应向量 而
是观测到的响应向量 而 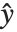 是响应向量的预测值. "HatDiagonal" 给我们提供了帽子矩阵的对角线元素. "CatcherMatrix" 是满足
是响应向量的预测值. "HatDiagonal" 给我们提供了帽子矩阵的对角线元素. "CatcherMatrix" 是满足  的矩阵
的矩阵 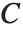 ,此处
,此处 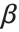 是拟合参数向量.
是拟合参数向量.
"FitDifferences" 给出 DFFITS值,它提供了用于测量每个数据点对拟合或预测值影响的一个度量. 第 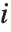 个DFFITS 值由
个DFFITS 值由 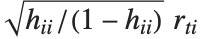 给出,其中
给出,其中 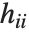 是第
是第 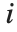 个帽子对角元素值,而
个帽子对角元素值,而 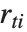 是第
是第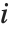 个学生化残差.
个学生化残差.
"BetaDifferences" 给出了DFBETAS值,它提供了用于测量每个数据点对于模型参数的影响的一个度量. 对于一个有 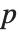 个参数的模型来说,"BetaDifferences" 的第
个参数的模型来说,"BetaDifferences" 的第 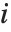 个元素是一个长度为
个元素是一个长度为 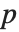 的列表,其中第
的列表,其中第 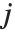 个值给我们提供了数据点
个值给我们提供了数据点  对于模型的第
对于模型的第  个参数的影响的测量. 第
个参数的影响的测量. 第 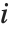 个 "BetaDifferences" 向量可以写成
个 "BetaDifferences" 向量可以写成 ,其中
,其中 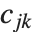 是捕集矩阵的第
是捕集矩阵的第 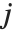
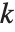 个元素.
个元素.
| "MeanPredictionBands" | 均值预测的置信带 |
| "MeanPredictionConfidenceIntervals" | 均值预测的置信区间 |
| "MeanPredictionConfidenceIntervalTable" | 均值预测的置信区间表 |
| "MeanPredictionConfidenceIntervalTableEntries" | 表中数值的非格式化数组表示 |
| "MeanPredictionErrors" | 均值预测的标准误差 |
| "PredictedResponse" | 数据的拟合值 |
| "SinglePredictionBands" | 基于单观测值的置信带 |
| "SinglePredictionConfidenceIntervals" | 单观测值的预测响应的置信区间 |
| "SinglePredictionConfidenceIntervalTable" | 单观测值的预测响应的置信区间表 |
| "SinglePredictionConfidenceIntervalTableEntries" | 表中数据的非格式化数组表示 |
| "SinglePredictionErrors" | 单观测值的预测响应的标准误差 |
置信区间的表格化结果可以用 "MeanPredictionConfidenceIntervalTable" 和"SinglePredictionConfidenceIntervalTable" 得到. 这包括观测到得和预测到的响应值、标准误差估计和每个点的置信区间. 均值预测的置信区间经常被简单称为置信区间. 而单个的预测置信区间经常被称为为预测区间.
均值预测区间给出当预测者固定时响应值 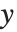 的置信区间,并且由
的置信区间,并且由 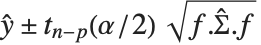 给出,其中
给出,其中 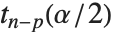 是学生
是学生 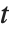 分布的
分布的 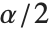 分位数,自由度为
分位数,自由度为  ,
,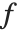 是在固定预测值上计算得到的基本函数构成的向量,而
是在固定预测值上计算得到的基本函数构成的向量,而  是参数的估计协方差矩阵. 单个预测区间提供了当预测值固定时,对
是参数的估计协方差矩阵. 单个预测区间提供了当预测值固定时,对  值进行预测时的置信区间,并且由
值进行预测时的置信区间,并且由  给出,其中
给出,其中 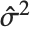 是估计误差方差.
是估计误差方差.
优度检验度量用于评估一个模型拟合的效果或者用于比较模型. 决定系数 "RSquared" 是模型平方和和总平方和之间的比率. "AdjustedRSquared" 用以惩罚模型中所用的参数数目,它可以表示为  .
.
广义线性模型
线性模型可以被视为具有如下特点的模型:每个响应值 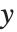 都等于一个服从正态分布的观测值,而该正态分布相应的均值是
都等于一个服从正态分布的观测值,而该正态分布相应的均值是 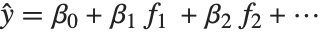 . 广义线性模型则扩展成为
. 广义线性模型则扩展成为 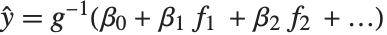 的形式,每个
的形式,每个 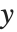 值假定服从一个已知指数族形式的分布,该指数分布相应的均值是
值假定服从一个已知指数族形式的分布,该指数分布相应的均值是  ,而
,而 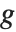 是指数族支撑上的可逆函数. 这种类型的模型可以通过 GeneralizedLinearModelFit 得到.
是指数族支撑上的可逆函数. 这种类型的模型可以通过 GeneralizedLinearModelFit 得到.
| GeneralizedLinearModelFit[{y1,y2,…},{f1,f2,…},x] | 获取一个具有基函数 fi 和一个单独的预测变量 x 的广义线性模型 |
| GeneralizedLinearModelFit[{{x11,x12,…,y1},{x21,x22,…,y2}},{f1,f2,…},{x1,x2,…}] | 获取一个具有多个预测变量 xi 的广义线性模型 |
| GeneralizedLinearModelFit[{m,v}] | 基于一个设计矩阵 m 和响应向量 v 获取一个广义线性模型 |
可逆函数  被称为链接函数. 而线性组合
被称为链接函数. 而线性组合 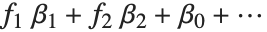 则称为线性预测. 常见的特例包括有恒等关联函数和高斯或正态指数族分布的线性回归模型,概率的logit模型和probit模型,用来计数的泊松模型,还有伽马(gamma)和逆高斯模型.
则称为线性预测. 常见的特例包括有恒等关联函数和高斯或正态指数族分布的线性回归模型,概率的logit模型和probit模型,用来计数的泊松模型,还有伽马(gamma)和逆高斯模型.
误差方差是预测值 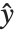 的函数,并且在相差一个被称为扩散参数的常量
的函数,并且在相差一个被称为扩散参数的常量 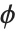 的情况下由分布来定义. 我们可以把一个拟合值
的情况下由分布来定义. 我们可以把一个拟合值  的误差方差写作
的误差方差写作  ,此处
,此处 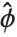 是从观测值和预测到的响应值得到的扩散参数的估计,而
是从观测值和预测到的响应值得到的扩散参数的估计,而  是和在
是和在 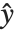 求值的指数族相关联的方差函数.
求值的指数族相关联的方差函数.
Logit和probit模型是常见的概率二项模型. logit模型的链接函数是  而probit模型的链接是标准正态分布
而probit模型的链接是标准正态分布  的逆累积分布函数. 这种类型的模型可以通过GeneralizedLinearModelFit 利用ExponentialFamily->"Binomial" 和合适的 LinkFunction 或者通过 LogitModelFit 和 ProbitModelFit 进行拟合.
的逆累积分布函数. 这种类型的模型可以通过GeneralizedLinearModelFit 利用ExponentialFamily->"Binomial" 和合适的 LinkFunction 或者通过 LogitModelFit 和 ProbitModelFit 进行拟合.
| LogitModelFit[data,funs,vars] | 获取一个具有基本函数 funs 和预测变量 vars 的 logit 模型 |
| LogitModelFit[{m,v}] | 获取一个基于设计矩阵 m 和响应向量 v 的 logit 模型 |
| ProbitModelFit[data,funs,vars] | 获取一个对 data 进行拟合的 probit 模型 |
| ProbitModelFit[{m,v}] | 获取一个对设计矩阵 m 和响应向量 v 进行拟合的 probit 模型 |
参数估计可以通过迭代重加权最小二乘算法获取,这里的权重可以通过设定的分布的方差函数获取. GeneralizedLinearModelFit 的选项包括:用于迭代拟合的选项(比如 PrecisionGoal )、用于模型描述的选项(比如 LinkFunction )和用于进一步分析的选项(比如 ConfidenceLevel ).
选项名
|
默认值
| |
| AccuracyGoal | Automatic | 目标准确度 |
| ConfidenceLevel | 95/100 | 参数和预测所用的置信水平 |
| CovarianceEstimatorFunction | "ExpectedInformation" | 参数协方差矩阵的估计方法 |
| DispersionEstimatorFunction | Automatic | 用以估计扩散参数的函数 |
| ExponentialFamily | Automatic | y 的指数族分布 |
| IncludeConstantBasis | True | 是否要包括常量基函数 |
| LinearOffsetFunction | None | 在线性预测子里的已知偏移量 |
| LinkFunction | Automatic | 模型的链接函数 |
| MaxIterations | Automatic | 需要使用的最大迭代次数 |
| NominalVariables | None | 名义变量或分类变量 |
| PrecisionGoal | Automatic | 目标精确度 |
| Weights | Automatic | 数据元素的权值 |
| WorkingPrecision | Automatic | 内部计算所用的精确度 |
LogitModelFit 和 ProbitModelFit 的选项和 GeneralizedLinearModelFit 的相同,除了 ExponentialFamily 和 LinkFunction. 这些是由 logit 模型或 probit 模型定义的,所以不是 LogitModelFit 和 ProbitModelFit 的选项.
ExponentialFamily 可以是 "Binomial"、"Gamma"、"Gaussian"、"InverseGaussian"、"Poisson" 或是"QuasiLikelihood". 二项模型对于从0 到 1 的响应是有效的. 泊松模型对于非负整数响应是有效的. 高斯或正态模型对于实响应是有效的. 伽马模型和逆高斯模型对于正响应是有效的. 拟似然模型用方差异函数 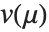 的形式定义了一个分布结构,使得对第
的形式定义了一个分布结构,使得对第 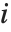 个数据点的拟似然函数的对数值由
个数据点的拟似然函数的对数值由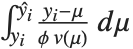 给出. 对于一个"QuasiLikelihood" 模型的方差函数可以通过ExponentialFamily->{"QuasiLikelihood", "VarianceFunction"->fun} 用选项的形式来设定,这里 fun 是一个将被用于拟合值的纯函数.
给出. 对于一个"QuasiLikelihood" 模型的方差函数可以通过ExponentialFamily->{"QuasiLikelihood", "VarianceFunction"->fun} 用选项的形式来设定,这里 fun 是一个将被用于拟合值的纯函数.
ExponentialFamily、IncludeConstantBasis、LinearOffsetFunction、LinkFunction、NominalVariables 和 Weights 都定义了模型结构和优化标准的一些方面,并且只能在 GeneralizedLinearModelFit 范围内被设定. 所有其他选项可以或者在 GeneralizedLinearModelFit 里被设定,或者当取得结果和诊断时被传递给 FittedModel 对象来设定. 在计算 FittedModel 对象时设置的选项优先于在拟合时给 GeneralizedLinearModelFit 的设置.
| "BasisFunctions" | 基函数列表 |
| "BestFit" | 拟合函数 |
| "BestFitParameters" | 参数估计 |
| "Data" | 输入数据或者设计矩阵和响应向量 |
| "DesignMatrix" | 模型的设计矩阵 |
| "Function" | 最佳拟合纯函数 |
| "LinearPredictor" | 拟合线性组合 |
| "Response" | 输入数据里的响应值 |
"BestFitParameters" 对基函数给出参数估计. "BestFit" 给出拟合函数 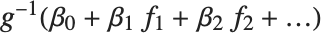 ,而 "LinearPredictor" 给出线性组合
,而 "LinearPredictor" 给出线性组合  . "BasisFunctions" 给出函数
. "BasisFunctions" 给出函数  的列表,其中当模型中有常量时,
的列表,其中当模型中有常量时,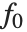 为常量1. "DesignMatrix" 是基本函数的设计矩阵或模型矩阵.
为常量1. "DesignMatrix" 是基本函数的设计矩阵或模型矩阵.
| "Deviances" | 偏差 |
| "DevianceTable" | 偏差表 |
| "DevianceTableDegreesOfFreedom" | 表中的自由度差 |
| "DevianceTableDeviances" | 表中的偏差差值 |
| "DevianceTableEntries" | 表中数据的非格式化数组表示 |
| "DevianceTableResidualDegreesOfFreedom" | 表中的残差自由度 |
| "DevianceTableResidualDeviances" | 表中的残差偏差 |
| "EstimatedDispersion" | 估计的扩散参数 |
| "NullDeviance" | 空(null)模型偏差 |
| "NullDegreesOfFreedom" | 空(null)模型自由度 |
| "ResidualDeviance" | 模型偏差和null偏差的差值 |
| "ResidualDegreesOfFreedom" | 模型自由度和null自由度的差值 |
偏差和偏差表是对线性模型中的方差分析所给出的模型分解的推广. 一个单独的数据点的偏差是 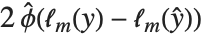 ,其中
,其中 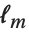 是拟合模型的对数似然函数. "Deviances" 给出所有数据点的偏差值列表. 而所有偏差值的和就是模型偏差. 模型偏差可以被分解,如同线性模型的方差分析表(ANOVA table)中的平方和那样. 完全模型是预测值与数据相同的模型.
是拟合模型的对数似然函数. "Deviances" 给出所有数据点的偏差值列表. 而所有偏差值的和就是模型偏差. 模型偏差可以被分解,如同线性模型的方差分析表(ANOVA table)中的平方和那样. 完全模型是预测值与数据相同的模型.
同平方和一样,偏差是可加的. 表的偏差列告诉我们当加入给定的基函数时,模型偏差的增加值. 残差偏差列告诉我们模型偏差和包括表中前面所有项的子模型的偏差的差值. 对于大的样本,偏差增加值基本上近似于 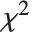 分布,其自由度等于表中基函数的自由度.
分布,其自由度等于表中基函数的自由度.
| "AnscombeResiduals" | 站点残差 |
| "DevianceResiduals" | 偏差残差 |
| "FitResiduals" | 实际响应和预测响应的差值 |
| "LikelihoodResiduals" | 似然残差 |
| "PearsonResiduals" | 皮尔森残差 |
| "StandardizedDevianceResiduals" | 标准偏差残差 |
| "StandardizedPearsonResiduals" | 标准化皮尔森残差 |
| "WorkingResiduals" | 工作残差 |
如果 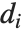 和
和  是第
是第 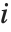 个数据点的偏差和残差,则第
个数据点的偏差和残差,则第 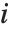 个偏差残差由
个偏差残差由  给出. 第
给出. 第 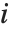 个皮尔逊残差被定义为
个皮尔逊残差被定义为 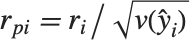 ,其中
,其中 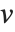 是指数族分布的方差函数. 标准偏差残差和标准皮尔森残差包括除以
是指数族分布的方差函数. 标准偏差残差和标准皮尔森残差包括除以  , 其中
, 其中 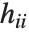 是帽子矩阵的第
是帽子矩阵的第 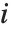 个对角线元素. "LikelihoodResiduals" 值把偏差和皮尔森残差组合起来. 第
个对角线元素. "LikelihoodResiduals" 值把偏差和皮尔森残差组合起来. 第 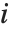 个似然残差可以表示为
个似然残差可以表示为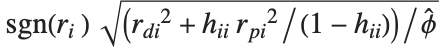 .
.
| "CorrelationMatrix" | 渐近参数相关矩阵 |
| "CovarianceMatrix" | 渐近参数协方差矩阵 |
| "ParameterConfidenceIntervals" | 参数置信区间 |
| "ParameterConfidenceIntervalTable" | 拟合参数置信区间表 |
| "ParameterConfidenceIntervalTableEntries" | 表中数值的非格式化数组表示 |
| "ParameterConfidenceRegion" | 椭圆参数置信区域 |
| "ParameterTableEntries" | 表中数值的非格式化数组表示 |
| "ParameterErrors" | 参数估计的标准误差 |
| "ParameterPValues" | 参数 |
| "ParameterTable" | 拟合参数信息表 |
| "ParameterZStatistics" | 参数估计的 |
"CovarianceMatrix" 给我们提供了拟合参数间的协方差,其和线性模型中的定义十分相似. 在CovarianceEstimatorFunction->"ExpectedInformation" 设置下,启用从迭代拟合得到的预期信息量矩阵. 该矩阵为  ,其中
,其中 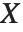 是设计矩阵而
是设计矩阵而  是从最后一步拟合得到的权值对角矩阵. 这些权值既包括由Weights 选项描述的权值也包括与分布的方差函数相关的权值. 采用 CovarianceEstimatorFunction->"ObservedInformation" 设置时,矩阵由
是从最后一步拟合得到的权值对角矩阵. 这些权值既包括由Weights 选项描述的权值也包括与分布的方差函数相关的权值. 采用 CovarianceEstimatorFunction->"ObservedInformation" 设置时,矩阵由 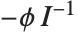 给出,其中
给出,其中  是观察到的 Fisher 信息量矩阵,该矩阵是和模型参数有关的对数似然函数的Hessian矩阵.
是观察到的 Fisher 信息量矩阵,该矩阵是和模型参数有关的对数似然函数的Hessian矩阵.
"CorrelationMatrix" 是和参数估计相关的相关系数矩阵. "ParameterErrors" 和协方差矩阵的对角线元素的平方根等价. "ParameterTable" 和 "ParameterConfidenceIntervalTable" 包含单个参数估计,参数检验的显著性,以及置信区间的信息. 对于广义线性模型的测试统计量来说,渐近地服从正态分布.
| "AdjustedLikelihoodRatioIndex" | Ben‐Akiva 和 Lerman 调整似然比指标 |
| "AIC" |
赤池信息量准则(AIC)
|
| "BIC" |
贝叶斯信息量准则(BIC)
|
| "CoxSnellPseudoRSquared" | Cox 和 Snell 伪 |
| "CraggUhlerPseudoRSquared" | Cragg 和 Uhler 伪 |
| "EfronPseudoRSquared" | Efron 伪 |
| "LikelihoodRatioIndex" | McFadden 似然比指标 |
| "LikelihoodRatioStatistic" | 似然比 |
| "LogLikelihood" | 拟合模型的对数似然值 |
| "PearsonChiSquare" | 皮尔森 |
"LogLikelihood" 是拟合模型的对数似然值. "AIC" 和 "BIC" 是被惩罚的对数似然度量方法 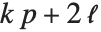 , 其中
, 其中 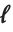 是拟合模型的对数似然值,
是拟合模型的对数似然值, 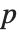 是估计参数数目(包括了扩散参数),对于一个有
是估计参数数目(包括了扩散参数),对于一个有 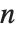 个数据点的模型来说,对 "AIC" ,
个数据点的模型来说,对 "AIC" , 是
是 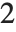 ,而对 "BIC" 是
,而对 "BIC" 是  . "LikelihoodRatioStatistic" 由
. "LikelihoodRatioStatistic" 由  给出,其中
给出,其中 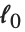 是空(null) 模型的对数似然值.
是空(null) 模型的对数似然值.
许多优度检验方法把  从线性回归推广为或是可解释变差的度量,或是一个基于似然方法的度量. "CoxSnellPseudoRSquared" 由
从线性回归推广为或是可解释变差的度量,或是一个基于似然方法的度量. "CoxSnellPseudoRSquared" 由 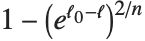 给出. "CraggUhlerPseudoRSquared" 是 Cox 和 Snell 度量的尺度化版本
给出. "CraggUhlerPseudoRSquared" 是 Cox 和 Snell 度量的尺度化版本 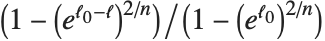 . "LikelihoodRatioIndex" 包含了对数似然比
. "LikelihoodRatioIndex" 包含了对数似然比  , 而 "AdjustedLikelihoodRatioIndex" 利用惩罚参数数目来调整
, 而 "AdjustedLikelihoodRatioIndex" 利用惩罚参数数目来调整  . "EfronPseudoRSquared" 利用
. "EfronPseudoRSquared" 利用  的平方和解释,并且可以表示为
的平方和解释,并且可以表示为  ,其中
,其中  是第
是第  个残差而
个残差而  是响应
是响应  的均值.
的均值.
非线性模型
一个非线性最小二乘模型是线性模型的一个扩展,这里模型可以不是基函数的线性组合. 误差仍然可以假设为独立和呈正态分布的. 这种类型的模型可以用 NonlinearModelFit 函数拟合.
| NonlinearModelFit[{y1,y2,…},form,{β1,…},x] | 获取一个具有包含参数 βi 的函数 form 和一个单参数预测变量 x 的非线性模型 |
| NonlinearModelFit[{{x11,…,y1},{x21,…,y2}},form,{β1,…},{x1,…}] | 获取一个作为具有多个预测变量 xi 的函数的非线性模型 |
| NonlinearModelFit[data,{form,cons},{β1,…},{x1,…}] | 获取一个受 cons 约束的非线性模型 |
非线性模型的形式为 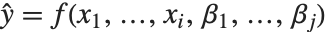 ,其中
,其中 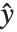 是拟合或预测值,
是拟合或预测值,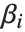 是要拟合的参数,而
是要拟合的参数,而 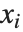 是预测变量. 与任何非线性优化问题相同,有必要对参数选择一个良好的初始值. 我们可以设置一个和 FindFit 的参数指定相同的初始值.
是预测变量. 与任何非线性优化问题相同,有必要对参数选择一个良好的初始值. 我们可以设置一个和 FindFit 的参数指定相同的初始值.
选项名
|
默认值
| |
| AccuracyGoal | Automatic | 目标准确度 |
| ConfidenceLevel | 95/100 | 用于参数和预测的置信水平 |
| EvaluationMonitor | None | 每次 expr 被计算时都要计算的表达式 |
| MaxIterations | Automatic | 所用的最大迭代次数 |
| Method | Automatic | 所用的方法 |
| PrecisionGoal | Automatic | 目标精确度 |
| StepMonitor | None | 每采取一个步骤时都要计算的表达式 |
| VarianceEstimatorFunction | Automatic | 估计误差方差的函数 |
| Weights | Automatic | 数据元素的权重 |
| WorkingPrecision | Automatic | 用于内部计算的精确度 |
NonlinearModelFit 的选项.
Weights 选项用于指定加权线性回归里的权值. 最优拟合是针对一个误差加权平方和的.
所有其他选项和初拟合后结果的计算相关. 可以在 NonlinearModelFit 里设置,用于拟合过程及对从FittedModel 对象得到的结果设置默认值. 这些选项页可以在一个已经建立好的 FittedModel 对象里设置,用以重载最初赋给 NonlinearModelFit 的选项值.
| "FitResiduals" | 实际响应和预测响应间的差值 |
| "StandardizedResiduals" | 拟合残差除以每个残差的标准误差 |
| "StudentizedResiduals" | 拟合残差除以单消除误差估计 |
和线性回归中一样,"FitResiduals" 给我们提供了观测值和预测值之间的差值  ,并且, "StandardizedResiduals" 和 "StudentizedResiduals" 是这些差值的尺度化表示.
,并且, "StandardizedResiduals" 和 "StudentizedResiduals" 是这些差值的尺度化表示.
第 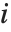 个标准化残差是
个标准化残差是 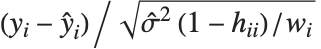 ,其中
,其中  是估计误差方差,
是估计误差方差, 是帽子矩阵的第
是帽子矩阵的第 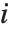 个对角线元素,而
个对角线元素,而 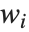 是第
是第 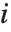 个数据点的权值,而第
个数据点的权值,而第 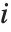 个学生化残差可以用第
个学生化残差可以用第 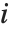 个单消除方差
个单消除方差  取代
取代 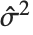 得到. 对于非线性模型,一个一级近似被用于设计矩阵,该矩阵是计算帽子矩阵所需要的.
得到. 对于非线性模型,一个一级近似被用于设计矩阵,该矩阵是计算帽子矩阵所需要的.
| "ANOVATable" | 方差分析表 |
| "ANOVATableDegreesOfFreedom" | 方差分析表中的自由度 |
| "ANOVATableEntries" | 表中数值的非格式化表示 |
| "ANOVATableMeanSquares" | 表中的均方误差 |
| "ANOVATableSumsOfSquares" | 表中的平方和 |
| "EstimatedVariance" | 误差方差估计 |
| "CorrelationMatrix" | 渐近参数相关系数矩阵 |
| "CovarianceMatrix" | 渐近参数协方差矩阵 |
| "ParameterBias" | 参数估计的估计偏移量 |
| "ParameterConfidenceIntervals" | 参数置信区间 |
| "ParameterConfidenceIntervalTable" | 拟合参数置信区间表 |
| "ParameterConfidenceIntervalTableEntries" | 表中数值的非格式化数组表示 |
| "ParameterConfidenceRegion" | 椭圆参数置信区域 |
| "ParameterErrors" | 参数估计的标准误差 |
| "ParameterPValues" | 参数 |
| "ParameterTable" | 拟合参数信息表 |
| "ParameterTableEntries" | 表中数值的非格式化数组表示 |
| "ParameterTStatistics" | 参数估计的 |
"CovarianceMatrix" 给我们提供了拟合参数间的近似协方差. 矩阵表示为  ,其中
,其中 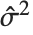 是方差估计,
是方差估计,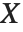 是模型线性近似的设计矩阵,而
是模型线性近似的设计矩阵,而  是权值的对角矩阵. "CorrelationMatrix" 是参数估计的关联相关矩阵. "ParameterErrors" 相当于协方差矩阵的对角线元素的平方根.
是权值的对角矩阵. "CorrelationMatrix" 是参数估计的关联相关矩阵. "ParameterErrors" 相当于协方差矩阵的对角线元素的平方根.
| "CurvatureConfidenceRegion" | 曲率诊断的置信区域 |
| "FitCurvatureTable" | 曲率诊断表 |
| "FitCurvatureTableEntries" | 表中数据相应的非格式化数组 |
| "MaxIntrinsicCurvature" | 最大内在曲率的度量 |
| "MaxParameterEffectsCurvature" | 最大参数效果曲率的度量 |
用于许多诊断的一级近似和具有线性参数的模型是等价的. 如果接近参数估计值的参数空间足够平,那么线性近似和任何依赖于一级近似的结果都可以被视为合理的. 曲率诊断被用于评价线性近似是否合理. "FitCurvatureTable" 给我们提供了一个曲率诊断表格.
"MaxIntrinsicCurvature" 和 "MaxParameterEffectsCurvature" 是参数空间在最佳参数值附近的法向和切向曲率的尺度化度量. "CurvatureConfidenceRegion" 是参数空间在最佳参数值附近的曲率半径的尺度化度量. 如果法向和切向曲率相对于 "CurvatureConfidenceRegion" 的值都较小的话,线性近似可以被认为是合适的. 有些经验法则建议直接和 "CurvatureConfidenceRegion" 值进行比较,而另一些则建议和该值的一半进行比较.
| "MeanPredictionBands" | 预测均值的置信带 |
| "MeanPredictionConfidenceIntervals" | 预测均值的置信区间 |
| "MeanPredictionConfidenceIntervalTable" | 预测均值置信区间表 |
| "MeanPredictionConfidenceIntervalTableEntries" | 表中数据的非格式化数组表示 |
| "MeanPredictionErrors" | 预测均值的标准差 |
| "PredictedResponse" | 数据的拟合值 |
| "SinglePredictionBands" | 基于单个观测值的置信带 |
| "SinglePredictionConfidenceIntervals" | 单个观测值的预测响应的置信区间 |
| "SinglePredictionConfidenceIntervalTable" | 单个观测值的预测响应的置信区间表 |
| "SinglePredictionConfidenceIntervalTableEntries" |
表中数据的非格式化数组表示
|
| "SinglePredictionErrors" |
单个的观测值的预测响应的标准差
|
置信区间的结果的表格由"MeanPredictionConfidenceIntervalTable" 和 "SinglePredictionConfidenceIntervalTable" 给出. 这些结果和通过LinearModelFit 求得的线性模型的结果类似,对于设计矩阵,同样采用一级近似.
"AdjustedRSquared"、"AIC"、"BIC" 和 "RSquared" 都是线性模型中度量的直接延伸. 决定系数 "RSquared" 是 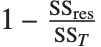 ,其中
,其中  是残差平方和,
是残差平方和, 是未修正的总平方和. 非线性模型的决定系数不象在线性模型中那样被解释成为解释方差的百分比,因为模型的平方和加上残差的平方和不一定等于总平方和. "AdjustedRSquared" 用以惩罚模型中所用的参数数目,其可以表示为
是未修正的总平方和. 非线性模型的决定系数不象在线性模型中那样被解释成为解释方差的百分比,因为模型的平方和加上残差的平方和不一定等于总平方和. "AdjustedRSquared" 用以惩罚模型中所用的参数数目,其可以表示为  .
.
在各种数值计算中,引入近似函数是很方便的. 近似函数可以看作近似实数的推广. 近似实数给出单个数值量的某种精度的值. 而近似函数给出单参数或多参数的量的某种精度的值. 例如,Wolfram 语言使用近似函数表示由 NDSolve 获得的微分方程的数值解,如 "微分方程的数值解" 中所述.
Wolfram 语言中的近似函数用 InterpolatingFunction 对象表示. 这些对象如同 "纯函数" 讨论的纯函数一样运行. 基本思想是当给定自变量的值时,该 InterpolatingFunction 对象求对应的近似函数值.
InterpolatingFunction 对象包含以插值为基础的近似函数表示. 其可以包含一系列点处的函数和导数值. 它假定函数在这些点之间是光滑的. 因此,在求特定自变量点处的函数时,InterpolatingFunction 对象用插值法求近似函数.
| Interpolation[{f1,f2,…}] | 构造一个近似函数使得在连续整数点处取值 fi |
| Interpolation[{{x1,f1},{x2,f2},…}] | |
构造一个近似函数使得在点 xi 处取值 fi | |
InterpolatingFunction 对象包含 Wolfram 语言所需的近似函数的所有信息. 然而在标准 Wolfram 语言输出格式中,仅明显给出 InterpolatingFunction 对象的定义域. 该 InterpolatingFunction 对象中实际的参数列表只用一对括号表示.
在标准输出格式中,仅明显给出 InterpolatingFunction 对象的定义域和输出类型:
| Interpolation[{{{x1},f1,df1,ddf1,…},…}] | |
构造在点 xi 处有指定导数的近似函数 | |
在缺省设置 InterpolationOrder->3 下,使用三次曲线,函数看起来很光滑:
提高 InterpolationOrder 对插值多项式的次数的设置可以使近似函数更光滑. 但是如果次数太高,可能产生摆动.
| ListInterpolation[{{f11,f12,…},{f21,…},…}] | |
用二维整数点网格处的值构造近似函数 | |
| ListInterpolation[list,{{xmin,xmax},{ymin,ymax}}] | |
假定列表值来自于指定定义域上的均匀空间网格处 | |
| ListInterpolation[list,{{x1,x2,…},{y1,y2,…}}] | |
假定列表值来自于指定网格线上的网格处 | |
产生的 InterpolatingFunction 对象具有三个自变量:
使用近似函数,经常得出 InterpolatingFunction 对象的复杂组合. 可以告诉 Wolfram 语言通过使用FunctionInterpolation 可以生成特定定义域上有效的单个 InterpolatingFunction 对象.
以下生成一个在 0 到 1 中有效的新的 InterpolatingFunction 对象:
这是生产一个嵌套 InterpolatingFunction 对象:
以下生成一个纯二维 InterpolatingFunction 对象:
| FunctionInterpolation[expr,{x,xmin,xmax}] | |
通过计算 expr 当 x 从 xmin 到 xmax 的值 | |
| FunctionInterpolation[expr,{x,xmin,xmax},{y,ymin,ymax},…] | |
构造多维近似函数 | |
| Fourier[{u1,u2,…,un}] | 离散傅立叶变换 |
| InverseFourier[{v1,v2,…,vn}] | 离散傅立叶反变换 |
不论给出的数据列表的长度是否是2的整数幂,Fourier 都能有效处理:
在不同的学科中,定义离散傅立叶变换有不同规定. 选项 FourierParameters 允许用户选择任何一种规定.
具有不同规定的 FourierParameters 的典型设置.
| Fourier[{{u11,u12,…},{u21,u22,…},…}] | |
二维离散傅立叶变换 | |
| FourierDCT[list] | 由实数组成的列表的傅立叶离散余弦变换 |
| FourierDST[list] | 由实数组成的列表的傅立叶离散正弦变换 |
| FourierDCT[list,m] | 类型为 m 的傅立叶离散余弦变换 |
| FourierDST[list,m] | 类型为 m 的傅立叶离散正弦变换 |
Wolfram 语言不需要 InverseFourierDCT 或者 InverseFourierDST 函数,由于 FourierDCT 和 FourierDST 在使用合适的类型时是其自身的反函数. 类型 1、2、3、4 的反变换分别是类型 1、3、2、4.
| ListConvolve[kernel,list] | 构造 kernel 与 list 的卷积 |
| ListCorrelate[kernel,list] | 构造 kernel 与 list 的相关 |
此情形中颠倒核元素的次序得出与卷积 ListConvolve 相同的结果:
在与一个核结合构造子列表中,在数据列表的末尾总有一个事情要做. 缺省时,ListConvolve 和 ListCorrelate 绝不会构造“延伸”数据列表的末端的子列表. 这意味着得到的输出通常比原数据列表短.
实际上,人们常常希望得到与原数据列表一样长的输出. 要做到这一点,需要包含延伸原数据列表一端或两端的子列表. 构造这些子列表所需的额外元素必须用某种“补丁”来填充. 缺省时,Wolfram 语言取原列表的拷贝作为补丁. 这样将列表周期地进行处理.
| ListCorrelate[kernel,list] | 不允许在两边延伸(结果比 list 短) |
| ListCorrelate[kernel,list,1] | 允许在右边延伸(结果与 list 的长度相同) |
| ListCorrelate[kernel,list,-1] | 允许在左边延伸(结果与 list 的长度相同) |
| ListCorrelate[kernel,list,{-1,1}] | 允许在两边延伸(结果比 list 长) |
| ListCorrelate[kernel,list,{kL,kR}] | 允许在左边和右边进行特定的延伸 |
一般情况下,ListCorrelate[kernel,list,{kL,kR}] 被设置为结果的第一个元素中包含 list 的第一个元素与 kernel 在位置 kL 处的元素的乘积,结果的最后一个元素中包含 list 的最后一个元素与 kernel 在位置 kR 处的元素的乘积. 缺省情形下,不允许在任何一端有延伸,因此对应于 ListCorrelate[kernel,list,{1,-1}].
| ListCorrelate[kernel,list,klist,p] | 用元素 p 补充 |
| ListCorrelate[kernel,list,klist,{p1,p2,…}] | |
用 pi 的循环进行补充 | |
| ListCorrelate[kernel,list,klist,list] | 用原数据的循环进行补充 |
| CellularAutomaton[rnum,init,t] | 从 |
| {a1,a2,…} | 值 ai 的明确列表 |
| {{a1,a2,…},b} | 在一个 b 背景(background)上叠加的值 ai |
| {{a1,a2,…},blist} | 在重复的 blist 的背景上叠加的值 ai |
| {{{{a11,a12,…},{d1}},…},blist} | 偏移量为 di 的值 aij |
如果用户给出初始值的明确列表,CellularAutomaton 将使该列表中的元素对应于系统中的所有元胞,并循环放置.
| n | |
| {n,k} | 具有 k 个颜色的一般最近邻规则 |
| {n,k,r} | 具有 k 种颜色和范围 r 的一般规则 |
| {n,{k,1}} | k-色最近邻总和规则 |
| {n,{k,1},r} | k-色范围 r 总和规则 |
| {n,{k,{wt1,wt2,…}},r} | 邻居 i 被赋于权重 wti 的规则 |
| {n,kspec,{{off1},{off2},…,{offs}}} | 具有指定偏移量的邻居的规则 |
| {lhs1->rhs1,lhs2->rhs2,…} | 邻居列表的明确替换 |
| {fun,{},rspec} | 通过对每个邻居列表应用函数 fun 获取的规则 |
在最简单的情况下,一个元胞自动机对每个元胞允许 k 个可能的值或者“颜色”,并且具有在每边至多有 r 个邻居的规则. “规则号码” n 的数位则指定对于邻居的每个可能的配置,新的元胞应该是什么颜色的.
对于一般元胞自动机规则,规则号码的每个数位指定了  个元胞组成的不同可能的邻居应该产生的颜色. 要找到哪个数位都对应于哪个邻居,实际就是把邻居中的元胞作为号码中的数位来处理. 对于一个
个元胞组成的不同可能的邻居应该产生的颜色. 要找到哪个数位都对应于哪个邻居,实际就是把邻居中的元胞作为号码中的数位来处理. 对于一个  元胞自动机,号码是通过 neig.{k^2,k,1} 从邻居中的元素 neig 的列表中得到.
元胞自动机,号码是通过 neig.{k^2,k,1} 从邻居中的元素 neig 的列表中得到.
有时候,考虑总和元胞自动机是方便的,其中每个元胞的新值仅取决于它的邻居的总和. 用户可以通过规则号码或者“代码”来指定总和元胞自动机,“代码”的每个数位表示给定总值的邻居. 该总值,举例来说,可以从 neig.{1,1,1} 得到.
任意  元胞自动机规则可以看作是对应于一个布尔函数. 在最简单的情况下,基本布尔函数如 And 或者 Nor 具有两个变量. 这在元胞自动机规则中方便地指定为偏移量 {{0},{1}}. 注意,为了与处理高维元胞自动机兼容,偏移量必须总是在列表中给出,即使对于一维元胞自动机也是如此.
元胞自动机规则可以看作是对应于一个布尔函数. 在最简单的情况下,基本布尔函数如 And 或者 Nor 具有两个变量. 这在元胞自动机规则中方便地指定为偏移量 {{0},{1}}. 注意,为了与处理高维元胞自动机兼容,偏移量必须总是在列表中给出,即使对于一维元胞自动机也是如此.
| CellularAutomaton[rnum,init,t] | 演化 t 步,保留所有步骤 |
| CellularAutomaton[rnum,init,{{t}}] | 演化 t 步,只保留最后一步 |
| CellularAutomaton[rnum,init,{spect}] | 只保留由 spect 指定的步骤 |
| CellularAutomaton[rnum,init] | 将规则演化一步,只给出最后一步 |
| CellularAutomaton[rnum,init,t] | 保留所有步骤和所有相关元胞 |
| CellularAutomaton[rnum,init,{spect,specx}] | |
仅保留指定的步骤和元胞 | |
与用户可以指定在元胞自动机演化中哪些步骤需要保留一样,用户也可以指定保留哪些元胞. 如果用户给出一个初始条件如 {{a1,a2,…},blist},那么为了指定那些元胞应该保留,rd 应该具有偏移量 0.
| All | 所有可以被指定初始条件影响的元胞 |
| Automatic | 所有与背景(默认)不同的区域中的元胞 |
| 0 | 与 aspec 开头对齐的元胞 |
| x | 右边的偏移量至多为 x 的元胞 |
| -x | 左边的偏移量至多为 x 的元胞 |
| {x} | 向右偏移量为 x 的元胞 |
| {-x} | 向左偏移量为 x 的元胞 |
| {x1,x2} | 偏移量从 x1 到 x2 的元胞 |
| {x1,x2,dx} | 元胞 x1,x1+dx,… |
如果用户给出初始条件如 {{a1,a2,…},blist},那么 CellularAutomaton 将总是以具有无穷数目的元胞进行元胞自动机运算. 通过使用 specx 如 {x1,x2} 用户可以告诉 CellularAutomaton 在输出中仅包含在指定偏移量 x1 到 x2 处的元胞. 默认情况下,CellularAutomaton 包括其值永远不与背景 blist 中的相同的足够远处的元胞.
一般来说,给定具有范围 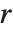 的元胞自动机规则,在每边距离
的元胞自动机规则,在每边距离 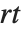 处的元胞原则上会受系统演化的影响. 当 specx 为 All 时,所有这些元胞都被包括;在 Automatic 的默认设置下,与 blist 中的值相同的元胞被修剪.
处的元胞原则上会受系统演化的影响. 当 specx 为 All 时,所有这些元胞都被包括;在 Automatic 的默认设置下,与 blist 中的值相同的元胞被修剪.
CellularAutomaton 相当直接地推广到了任意维数. 但是,在二维以上,总和及其他特殊类型的规则会变得更为有用,因为一般规则的规则表中的项数会迅速变成天文数字.
| {n,k,{r1,r2,…,rd}} | 具有 |
| {n,{k,1},{1,1}} | 二维九邻居总和规则 |
| {n,{k,{{0,1,0},{1,1,1},{0,1,0}}},{1,1}} | |
二维五邻居总和规则 | |
| {n,{k,{{0,k,0},{k,1,k},{0,k,0}}},{1,1}} | |
二维五邻居外层总和规则 | |