| StandardForm | TraditionalForm | |
| Abs[z] | 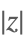 | ⋆ |
| AiryAi[z] |  | |
| AiryAiPrime[z] |  | |
| AiryBi[z] |  | |
| AiryBiPrime[z] |  | |
| Algebraics | 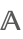 | ⋆ |
| And[p1,p2,…] | 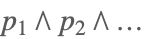 | |
| AngerJ[ν,x] | 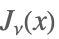 | * |
| AngerJ[ν,μ,x] | 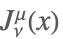 | * |
| AppellF1[a,b1,b2,c,x,y] | 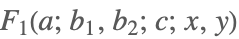 | ⋆ |
| ArcCos[z] | 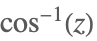 | |
| ArcCosh[z] | 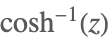 | |
| ArcCot[z] | 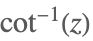 | |
| ArcCoth[z] | 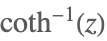 | |
| ArcCsc[z] | 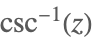 | |
| ArcCsch[z] | 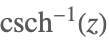 | |
| ArcSec[z] | 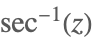 | |
| ArcSech[z] | 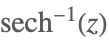 | |
| ArcSin[z] | 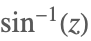 | |
| ArcSinh[z] | 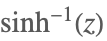 | |
| ArcTan[z] | 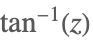 | |
| ArcTanh[z] | 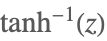 | |
| Arg[z] |  | |
| ArithmeticGeometricMean[a,b] | 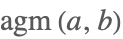 | ⋆ |
| BernoulliB[n] | 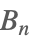 | ⋆ |
| BernoulliB[n,z] | 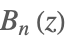 | ⋆ |
| BesselI[n,z] | 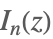 | |
| BesselJ[n,z] |  | |
| BesselK[n,z] |  | |
| BesselY[n,z] | 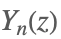 | |
| Beta[a,b] | 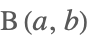 | ⋆ |
| Beta[z,a,b] | 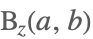 | ⋆ |
| Beta[z0,z1,a,b] | 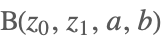 | ⋆ |
| BetaRegularized[z,a,b] | 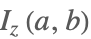 | ⋆ |
| BetaRegularized[z0,z1,a,b] | 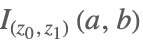 | ⋆ |
| Binomial[n,m] |  | ⋆ |
| Booleans | 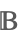 | ⋆ |
| C[n] | 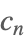 | ⋆ |
| CarmichaelLambda[n] | 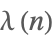 | ⋆ |
| Catalan |  | ⋆ |
| Ceiling[z] |  | |
| ChampernowneNumber[b] |  | * |
| ChebyshevT[n,x] | 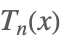 | |
| ChebyshevU[n,x] | 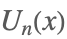 | |
| ClebschGordan[{j1,m1},{j2,m2},{j3,m3}] | 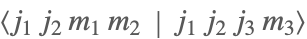 | ⋆ |
| Complexes |  | ⋆ |
| Conjugate[z] |  | * |
| Cos[z] |  | |
| Cos[z]p | 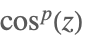 | |
| Cosh[z] |  | |
| Cosh[z]p |  | |
| CosIntegral[z] |  | |
| CoshIntegral[z] |  | |
| Cot[z] |  | |
| Cot[z]p |  | |
| Coth[z] |  | |
| Coth[z]p |  | |
| Csc[z] |  | |
| Csc[z]p | 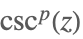 | |
| Csch[z] |  | |
| Csch[z]p |  | |
| Cyclotomic[n,z] |  | ⋆ |
| D[f[x]] | 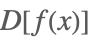 | |
| D[f[x],x] | 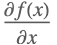 | |
| D[f[x],{x,2}] | 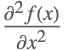 | |
| D[f[x],{x,n}] | 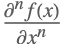 | |
| Dt[f[x]] | 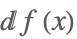 | ⋆ |
| Dt[f[x],x] | 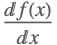 | |
| Dt[f[x],{x,2}] | 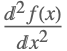 | |
| Dt[f[x],{x,n}] | 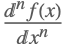 | |
| DawsonF[x] |  | * |
| DedekindEta[t] | 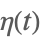 | ⋆ |
| Derivative[1][f] | 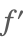 | |
| Derivative[2][f] | 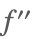 | |
| Derivative[d1,…][f] | 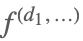 | ⋆ |
| Det[A] |  | ⋆ |
| DifferenceDelta[f,i] | 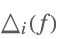 | * |
| DifferenceDelta[f,{i,n}] | 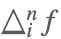 | * |
| DifferenceDelta[f,{i,n,h}] | 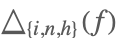 | * |
| DifferenceDelta[f,i,j,...] | 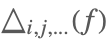 | * |
| DiracDelta[x1,x2,…] | 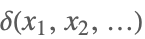 | ⋆ |
| DiscreteDelta[n1,n2,…] | 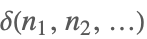 | ⋆ |
| DiscreteRatio[f,i] | 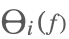 | * |
| DiscreteRatio[f,{i,n}] |  | * |
| DiscreteRatio[f,{i,n,h} | 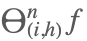 | * |
| DiscreteRatio[f,i,j,...] | 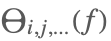 | * |
| DiscreteShift[f,i] |  | * |
| DiscreteShift[f,{i,n}] |  | * |
| DiscreteShift[f,{i,n,h}] | 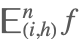 | * |
| DiscreteShift[f,i,j,...] |  | * |
| DivisorSigma[k,n] | 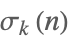 | ⋆ |
| EllipticE[m] |  | |
| EllipticE[ϕ,m] | 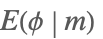 | ⋆ |
| EllipticF[ϕ,m] | 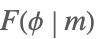 | ⋆ |
| EllipticK[m] |  | |
| EllipticNomeQ[m] | 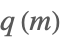 | ⋆ |
| EllipticPi[n,m] |  | ⋆ |
| EllipticPi[n,ϕ,m] | 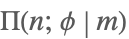 | ⋆ |
| EllipticTheta[a,u,q] | 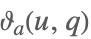 | |
| EllipticThetaPrime[a,u,q] | 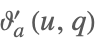 | ⋆ |
| Erf[z] |  | |
| Erf[z0,z1] | 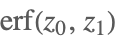 | |
| Erfc[z] |  | |
| Erfi[z] |  | |
| EulerE[n] | 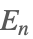 | ⋆ |
| EulerE[n,z] |  | ⋆ |
| EulerGamma | 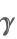 | ⋆ |
| EulerPhi[n] | 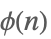 | ⋆ |
| ExpIntegralE[n,z] | 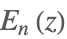 | ⋆ |
| ExpIntegralEi[z] |  | |
| Fibonacci[n] | 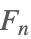 | ⋆ |
| Fibonacci[n,z] | 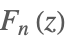 | ⋆ |
| Floor[z] | 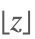 | |
| FourierTransform[expr,t,s] | 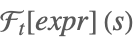 | |
| FourierTransform[expr,{t1,t2,…},{s1,s2,…}] | 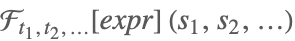 | |
| FractionalPart[x] | 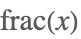 | |
| FresnelC[z] |  | |
| FresnelS[z] |  | |
| Gamma[z] |  | |
| Gamma[a,z] | 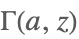 | |
| Gamma[a,z1,z2] | 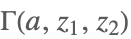 | |
| GammaRegularized[a,z] | 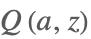 | ⋆ |
| GammaRegularized[a,z0,z1] | 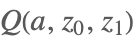 | ⋆ |
| GCD[n1,n2,…] | 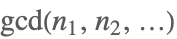 | |
| GegenbauerC[n,x] | 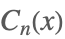 | |
| GegenbauerC[n,m,x] | 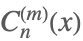 | |
| Glaisher | 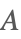 | |
| GoldenRatio |  | ⋆ |
| HarmonicNumber[n] |  | ⋆ |
| HarmonicNumber[n,r] | 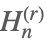 | ⋆ |
| HeavisideLambda[x] | 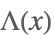 | * |
| HeavisideLambda[x1,x2,…] | 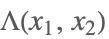 | * |
| HeavisidePi[x] | 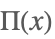 | * |
| HeavisidePi[x1,x2,…] | 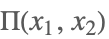 | * |
| HermiteH[n,x] | 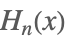 | |
| Hypergeometric0F1[a,z] | 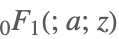 | ⋆ |
| Hypergeometric0F1Regularized[a,z] | 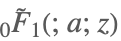 | ⋆ |
| Hypergeometric1F1[a,b,z] | 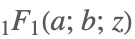 | ⋆ |
| Hypergeometric1F1Regularized[a,b,z] | 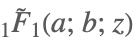 | ⋆ |
| Hypergeometric2F1[a,b,c,z] | 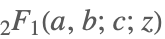 | ⋆ |
| Hypergeometric2F1Regularized[a,b,c,z] | 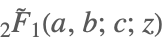 | ⋆ |
| HypergeometricPFQ[{a1,…,ap},{b1,…,bq},z] | 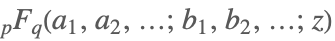 | ⋆ |
| HypergeometricPFQRegularized[{a1,…,ap},{b1,…,bq},z] | 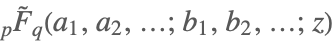 | ⋆ |
| HypergeometricU[a,b,z] | 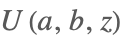 | ⋆ |
| Implies[a,b] |  | ⋆ |
| Integers |  | ⋆ |
| Integrate[expr,x] | 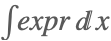 | |
| Integrate[expr,x1,y,z] |  | |
| Integrate[expr,{x,a,b}] | 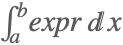 | |
| Integrate[expr,{x,a,b},{y,m,n},{z,p,q}] |  | |
| Inverse[A] | 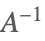 | |
| InverseBetaRegularized[s,a,b] | 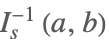 | ⋆ |
| InverseBetaRegularized[z0,s,a,b] | 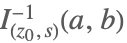 | ⋆ |
| InverseEllipticNomeQ[q] | 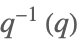 | ⋆ |
| InverseErf[z0,s] | 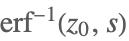 | |
| InverseFourierTransform[expr,s,t] |  | |
| InverseFourierTransform[expr,{s1,s2,…},{t1,t2,…}] |  | |
| InverseFunction[f] | 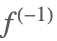 | ⋆ |
| InverseJacobiCD[u,m] | 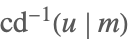 | ⋆ |
| InverseJacobiCN[u,m] | 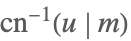 | ⋆ |
| InverseJacobiCS[u,m] | 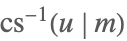 | ⋆ |
| InverseJacobiDC[u,m] | 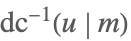 | ⋆ |
| InverseJacobiDN[u,m] | 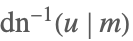 | ⋆ |
| InverseJacobiDS[u,m] | 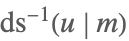 | ⋆ |
| InverseJacobiNC[u,m] | 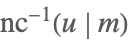 | ⋆ |
| InverseJacobiND[u,m] | 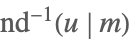 | ⋆ |
| InverseJacobiNS[u,m] | 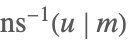 | ⋆ |
| InverseJacobiSC[u,m] | 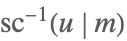 | ⋆ |
| InverseJacobiSD[u,m] | 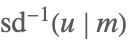 | ⋆ |
| InverseJacobiSN[u,m] | 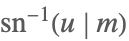 | ⋆ |
| InverseLaplaceTransform[expr,s,t] |  | |
| InverseLaplaceTransform[expr,{s1,s2,…},{t1,t2,…}] | 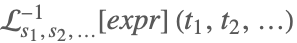 | |
| InverseWeierstrassP[p,{g2,g3}] | 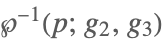 | |
| InverseZTransform[exp,z,n] | 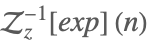 | |
| InverseZTransform[exp,{z1,z2,…},{n1,n2,…}] | 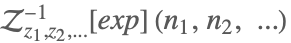 | |
| JacobiAmplitude[u,m] | 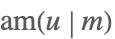 | |
| JacobiCD[u,m] | 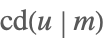 | ⋆ |
| JacobiCN[u,m] | 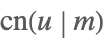 | ⋆ |
| JacobiCS[u,m] | 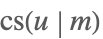 | ⋆ |
| JacobiDC[u,m] | 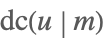 | ⋆ |
| JacobiDN[u,m] | 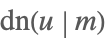 | ⋆ |
| JacobiDS[u,m] | 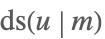 | ⋆ |
| JacobiNC[u,m] | 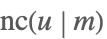 | ⋆ |
| JacobiND[u,m] | 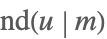 | ⋆ |
| JacobiNS[u,m] | 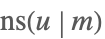 | ⋆ |
| JacobiSC[u,m] | 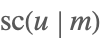 | ⋆ |
| JacobiSD[u,m] | 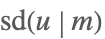 | ⋆ |
| JacobiSN[u,m] | 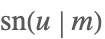 | ⋆ |
| JacobiP[n,a,b,x] | 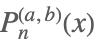 | |
| JacobiSymbol[n,m] |  | ⋆ |
| JacobiZeta[ϕ,m] | 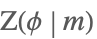 | ⋆ |
| Khinchin | 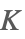 | * |
| KleinInvariantJ[τ] | 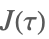 | ⋆ |
| KroneckerDelta[n1,n2,…] | 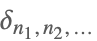 | ⋆ |
| LaguerreL[n,x] | 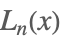 | |
| LaguerreL[n,a,x] | 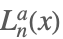 | |
| LegendreP[n,x] | 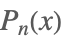 | ⋆ |
| LegendreP[n,m,x] | 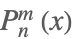 | ⋆ |
| LegendreP[n,m,a,z] |  | ⋆ |
| LaplaceTransform[expr,t,s] | 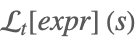 | |
| LaplaceTransform[expr,s,t] | 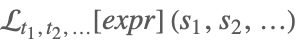 | |
| LCM[n1,n2,…] | 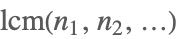 | |
| LegendreQ[n,x] | 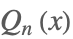 | ⋆ |
| LegendreQ[n,m,x] | 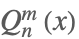 | ⋆ |
| LegendreQ[n,m,a,z] | 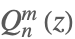 | ⋆ |
| LerchPhi[z,s,a] | 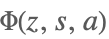 | ⋆ |
| Limit[f[x],x->a] | 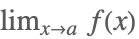 | |
| Limit[f[x],x->a,Direction->+1] | 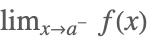 | |
| Limit[f[x],x->a,Direction->-1] | 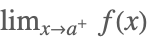 | |
| LiouvilleLambda[n] |  | * |
| Log[z] |  | |
| Log[b,z] |  | |
| Log[z]^p |  | |
| Log[b,z]^p |  | |
| LogGamma[z] |  | |
| LogIntegral[z] |  | |
| MangoldtLambda[n] | 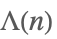 | * |
| MathieuCharacteristicA[r,q] | 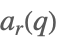 | ⋆ |
| MathieuCharacteristicB[r,q] | 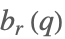 | ⋆ |
| Max[z] | 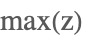 | |
| MeijerG[{{a1,…,an},{an+1,…,ap}},{{b1,…,bm},{bm+1,…,bq}},z] | 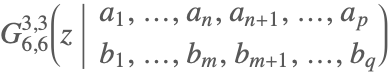 | ⋆ |
| MeijerG[{{a1,…,an},{an+1,…,ap}},{{b1,…,bm},{bm+1,…,bq}},z,r] | 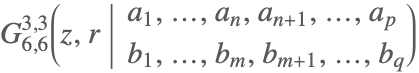 | ⋆ |
| Min[z] |  | |
| Mod[m,n] |  | ⋆ |
| ModularLambda[τ] | 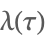 | ⋆ |
| MoebiusMu[n] | 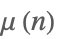 | ⋆ |
| Multinomial[n1,n2,…,nk] |  | ⋆ |
| MultiplicativeOrder[k,n] |  | |
| Nand[p1,p2,…] | 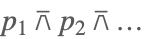 | |
| NevilleThetaC[u,m] | 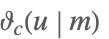 | ⋆ |
| NevilleThetaD[u,m] | 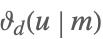 | ⋆ |
| NevilleThetaN[u,m] | 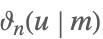 | ⋆ |
| NevilleThetaS[u,m] | 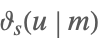 | ⋆ |
| Nor[p1,p2,…] | 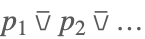 | |
| Not[p] | 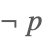 | |
| O[x] |  | |
| O[x]^n | 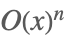 | |
| O[x,a] | 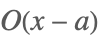 | |
| O[x,a]^n |  | |
| Or[p1,p2,…] | 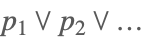 | |
| PartitionsP[z] | 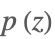 | ⋆ |
| PartitionsQ[z] |  | ⋆ |
| Piecewise[{{v1,c1},{v2,c2},…}] | 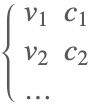 | ⋆ |
| Pochhammer[a,n] |  | ⋆ |
| PolyGamma[z] | 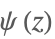 | ⋆ |
| PolyGamma[n,z] | 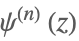 | ⋆ |
| PolyLog[ν,z] | 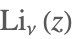 | ⋆ |
| PolyLog[ν,p,z] | 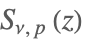 | ⋆ |
| PolynomialMod[poly,m] |  | ⋆ |
| PowerMod[a,b,n] |  | ⋆ |
| Prime[n] | 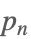 | ⋆ |
| PrimeNu[n] | 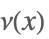 | * |
| PrimeOmega[n] |  | * |
| PrimePi[z] |  | ⋆ |
| PrimeZetaP[x] | 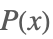 | * |
| Primes |  | ⋆ |
| ProductLog[z] |  | ⋆ |
| ProductLog[k,z] | 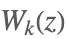 | ⋆ |
| QBinomial[n,m,q] | 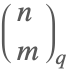 | * |
| QFactorial[n,q] | 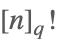 | * |
| QGamma[z,q] | 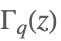 | * |
| QHypergeometricPFQ[{a1,…,at},{b1,…,bs},q,z] | 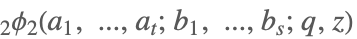 | * |
| QPochhammer[a,q,n] | 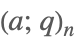 | * |
| QPochhammer[a,q] | 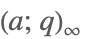 | * |
| QPochhammer[q] | 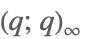 | * |
| QPolyGamma[z,q] | 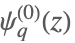 | * |
| QPolyGamma[n,z,q] | 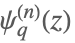 | * |
| RamanujanTau[n] | 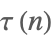 | ⋆ |
| Rationals |  | ⋆ |
| Reals | 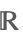 | ⋆ |
| Residue[z] |  | |
| RiemannR[x] | 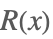 | * |
| RiemannSiegelTheta[t] | 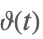 | ⋆ |
| RiemannSiegelZ[t] |  | ⋆ |
| Sec[z] |  | |
| Sec[z]p | 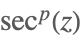 | |
| Sech[z] |  | |
| Sech[z]p |  | |
| Series[f[x],{x,a,0}] | 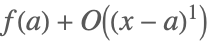 | ⋆ |
| Series[f[x],{x,a,1}] | 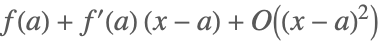 | ⋆ |
| Series[Tan[z^(2/3)],{z,0,3}] | 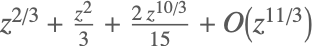 | ⋆ |
| Sign[z] |  | |
| Signature[e1,e2,…] | 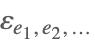 | ⋆ |
| Sin[z] |  | |
| Sin[z]p | 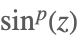 | |
| Sinh[z] |  | |
| Sinh[z]p | 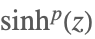 | |
| SinIntegral[z] |  | |
| SinhIntegral[z] |  | |
| SixJSymbol[{j1,j2,j3},{j4,j5,j6}] | 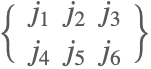 | ⋆ |
| SphericalHarmonicY[l,m,θ,ϕ] | 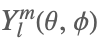 | ⋆ |
| SquaresR[d,n] | 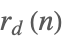 | * |
| StieltjesGamma[n] | 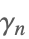 | ⋆ |
| StieltjesGamma[n,a] | 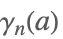 | * |
| StirlingS1[n,m] | 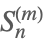 | ⋆ |
| StirlingS2[n,m] | 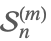 | ⋆ |
| StruveH[ν,z] | 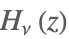 | ⋆ |
| StruveL[ν,z] | 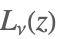 | ⋆ |
| Tan[z] |  | |
| Tan[z]p |  | |
| Tanh[z] |  | |
| Tanh[z]p |  | |
| ThreeJSymbol[{j1,m1},{j2,m2},{j3,m3}] | 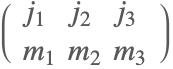 | ⋆ |
| Transpose[A] | 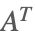 | |
| UnitBox[x] | 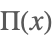 | * |
| UnitBox[x1,x2,…] | 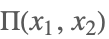 | * |
| UnitStep[x1,x2,…] | 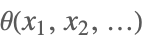 | ⋆ |
| UnitTriangle[x] | 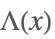 | * |
| UnitTriangle[x1,x2,…] | 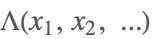 | * |
| WeberE[ν,x] | 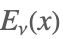 | * |
| WeberE[ν,μ,x] |  | * |
| WeierstrassP[u,{g2,g3}] | 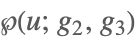 | |
| WeierstrassPPrime[u,{g2,g3}] | 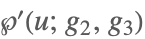 | ⋆ |
| WeierstrassSigma[u,{g2,g3}] | 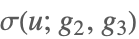 | ⋆ |
| WeierstrassZeta[u,{g2,g3}] | 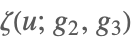 | ⋆ |
| Xor[p1,p2,…] | 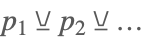 | |
| Zeta[s] |  | ⋆ |
| Zeta[s,a] | 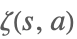 | ⋆ |
| ZTransform[exp,n,z] |  | |
| ZTransform[exp,{n1,n2,…},{z1,z2,…}] | 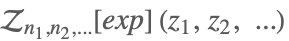 | |